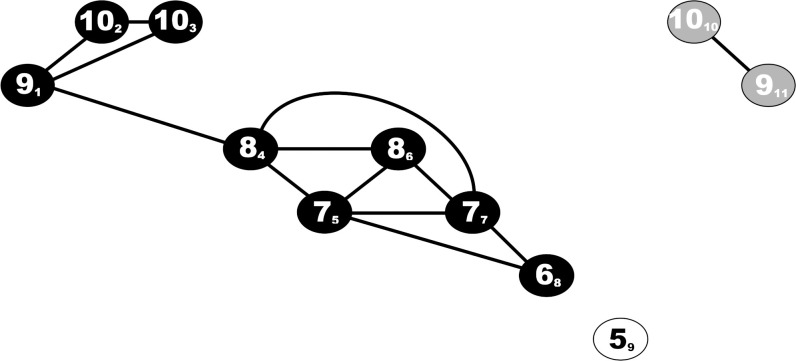
Fig 1. The similarity graph algorithm exemplified and explained within a k = 5 time series.

In this example the similarity graph algorithm transforms a time series S = (9,10,10,8,7,8,7,6,5,10,9) into a graph G, where each element of time series S corresponds to a node in V = {1,2,3,4,5,6,7,8,9,10,11}. The corresponding elements of S and nodes in V are identified as S_V in the figure. Two random nodes u and v are connected by an edge in G if and only if their distance is below a certain threshold k (|u-v| < k), and the ratio of the element values below a threshold defined as max (x_u, x_v) / min (x_u, x_v) < 1.2. In this example k = 5, and edges are drawn as solid lines in the illustration. The output of the time series are 13 edges, three components (black/white/grey) two bridges (9₁−8₄, 10₁₀−9₁₁), three missing edges between direct neighbors (10₃−8₄, 6₈−5₉ and 5₉−10₁₀), one time point without edges (5₉), and six 3-cliques (9₁−10₂−10₃), (8₄−7₅−8₆), (8₄−7₅−7₇), (7₅−6₈−7₇), (8₄−8₆−7₇), (8₆,7₇,7₅).