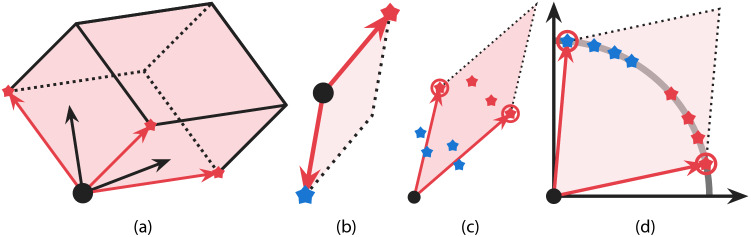
Figure 2.

Graphical explanation of (a) the log-determinant function, (b) the effect of ReLU, and (c and d) the effect of normalization. In all figures above, the black dot indicates the origin. (a) is a parallelotope spanned by vectors colored in red. (b) illustrates an example where the log-determinant function value for dissimilar vectors becomes small if vectors are allowed to have negative elements. Here and in the next two figures, points with different colors (red and blue) represent molecules with dissimilar properties, while those with the same colors have similar properties. (c) shows why maximizing the log-determinant function without normalization may result in a non-diverse selection, and (d) presents how normalization helps the log-determinant function maximization to select diverse vectors. Note that (d) is generally different from the normalized version of (c), i.e., vectors generated by the GNN with normalization are different from those obtained by normalizing vectors generated by the GNN without normalization. This is because the backpropagation is performed through the normalization layer, and thus the presence of the normalization layer affects how the GNN parameters are updated. As a result, the GNN is trained to generate molecular vectors so that the task-specific layer can predict molecular properties based on the angles of vectors, as in (d).