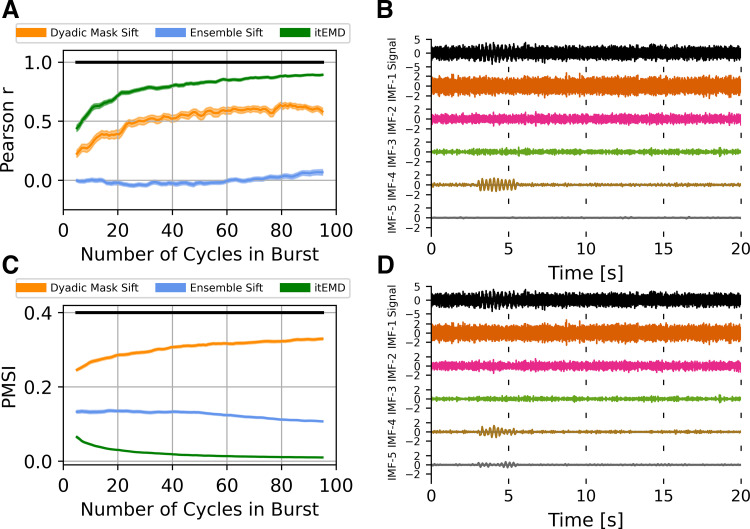
Figure 6.
Influence of signal sparsity on empirical mode decomposition (EMD) performance on simulated data. A: Pearson correlation coefficient between reconstructed and ground truth instantaneous frequency against increasing burst length. B: example iterated masking EMD (itEMD) sift results for σnoise = 1, FD = 68%, 10 cycles. C: pseudo-mode splitting index (PMSI) against burst length. Means ± standard error across n = 100 noise realizations (shaded) shown. Black line indicates regions where itEMD performs significantly better than the best existing technique with P < 0.01 (multiple comparisons Bonferroni corrected). The novel itEMD performs significantly better for a wide range of burst durations. D: example dyadic mask sift results for σnoise = 1, FD = 60%, 10 cycles in burst. Iterated sine function is captured by intrinsic mode function (IMF)-4 and IMF-5 due to mode mixing. FD, frequency distortion.