Automated segmentation of bi-ventricular contours in tissue phase mapping using deep learning

Abstract

Tissue phase mapping (TPM) is an MRI technique for quantification of regional biventricular myocardial velocities. Despite the potential, its clinical use is limited due to the requisite labor-intensive manual segmentation of cardiac contours for all time frames. The purpose of this study was to develop a deep learning (DL) network for automated segmentation of TPM images, without significant loss in segmentation and myocardial velocity quantification accuracy compared with manual segmentation. We implemented a multi-channel 3D (2D + time) dense U-Net that trained on magnitude and phase images and combined cross-entropy, dice, and Hausdorff distance loss terms to improve the segmentation accuracy and suppress unnatural boundaries. The dense U-Net was trained and tested with 150 multi-slice, multi-phase TPM scans(114 scans for training, 36 for testing) from 99 heart transplant (HTx) patients(44 females, 1–4 scans/patient), where the magnitude and velocity-encoded (V_x, V_y, V_z) images were used as input and the corresponding manual segmentation masks were used as reference. The accuracy of DL segmentation was evaluated using quantitative metrics (dice scores, Hausdorff distance) and linear regression and Bland-Altman analyses on the resulting peak radial and longitudinal velocities (V_r and V_z). The mean segmentation time was ~2 hours per patient for manual and 1.9 ± 0.3 seconds for DL. Our network produced good accuracy (median dice = 0.85 for left ventricle [LV], 0.64 for right ventricle [RV], Hausdorff distance = 3.17 pixels) compared with manual segmentation. Peak V_r and V_z measured from manual and DL segmentations were strongly correlated (R≥0.88) and in good agreement with manual analysis (mean difference and limits of agreement for V_z and V_r were −0.05±0.98cm/s and −0.06±1.18cm/s for LV, and −0.21±2.33cm/s and 0.46±4.00cm/s for RV, respectively). The proposed multi-channel 3D dense U-Net was capable of reducing the segmentation time by 3600-times, without significant loss in accuracy in tissue velocity measurements.

INTRODUCTION

Cine cardiovascular magnetic resonance (CMR) using balanced steady-state free precession (1) is the gold-standard imaging modality for the evaluation of cardiac function (2,3). Global cardiac functional parameters such as end diastolic volume, end systolic volume, stroke volume, ejection fraction, and mass of the left ventricle (LV) and right ventricle (RV) are routinely evaluated from cine CMR images. However, for most diseases, intramyocardial abnormalities may precede global functional abnormalities (e.g. ejection fraction). CMR has the ability to non-invasively characterize intramyocardial function using techniques such as myocardial tagging (4,5), strain-encoded (SENC) (6), cine displacement-encoded imaging with stimulated echoes (DENSE) (7,8), and tissue phase mapping (TPM) (9,10). These techniques have proven useful in diagnosing and monitoring abnormal myocardial function in a wide range of cardiovascular conditions including congenital heart diseases (11,12), cardiotoxicities (13,14), cardiac transplantation (15–17), left ventricular dyssynchrony (18,19), and various cardiomyopathies (20–22).

In this study, we will focus on TPM, which is a black-blood 2D cine phase contrast MRI pulse sequence with three-directional tissue velocity encoding for quantification of regional biventricular myocardial velocities (23). Recently, several studies have demonstrated significant differences in biventricular global and regional velocities in heart transplant (HTx) patients (adult and pediatric) with and without transplant rejection (15,16). Despite these studies demonstrating feasibility, the clinical translation of TPM is hampered by the requisite labor-intensive manual segmentation of the myocardial contours for all cardiac frames. In general, manual segmentation of TPM images is more challenging for the RV than the LV, because the former has thinner wall, highly trabeculated myocardium, and epicardial fat partially superimposing on the myocardial wall. For clinical translation of TPM, there is a need to automate segmentation of bi-ventricular contours.

The task of developing a post-processing tool to automate the segmentation of myocardial contours in TPM data from HTx patients is challenging due to several factors. First, the black-blood preparation module is not perfect and often produces residual blood signal, which makes it challenging to define the endocardial border. Second, metal artifacts from open chest surgery makes it challenging to define the epicardial contours, especially for the RV. Third, TPM with gradient echo readouts is inherently a low signal-to-noise-ratio (SNR) pulse sequence, thereby making segmentation sensitive to noise. Previous studies have reported automatic or semi-automatic segmentation tools using traditional machine learning or atlas based methods for TPM images with various degrees of success (24–28). A major disadvantage of such methods is that they often require prior knowledge to achieve satisfactory accuracy. To date, none of them have enabled TPM to be translated into clinical practice.

Deep learning (DL) has found many applications in medical imaging, including image reconstruction (29–31), segmentation (32–34), and disease classification (35–37). The major advantage of DL over traditional segmentation methods is that neural networks are good at automatically discovering intricate features from data for object detection and segmentation. Another advantage of DL over traditional segmentation methods is that the inference processing time is several orders of magnitude faster. In this study, we sought to develop a fully automated segmentation method for TPM images using DL and evaluate its accuracy compared with manual LV and RV contour delineation.

METHODS

Patient Demographics

This study was conducted in accordance with protocols approved by our institutional review board and was Health Insurance Portability and Accountability Act (HIPAA) compliant. All subjects provided informed consent in writing and agreed to future analysis of their data. We retrospectively identified 99 patients with heart transplantation (mean age = 50 ± 15 years; 55 males; 44 females) who participated in a longitudinal study, where each patient underwent 1–4 CMR scans for post HTx cardiac monitoring (median duration post HTx: 4.4 years; range: 6 days to 30 years). In total, 150 CMR scans were included in this study. For patients with more than one scan, there was a gap of at least three months between consecutive scans.

MRI Hardware

TPM scans were conducted on a 1.5T whole-body MRI scanner (MAGNETOM Aera or Avanto, Siemens Healthcare, Erlangen, Germany). The scanners were equipped with a gradient system capable of achieving a maximum gradient strength of 45 mT/m and maximum slew rate of 200 T/m/s. Body coil was used for radio-frequency excitation. Both body matrix and spine coil arrays (30–34 elements in total) were used for signal reception.

Pulse Sequence

TPM data were acquired in three short-axis slices at basal, mid-ventricular, and apical locations using a prospectively ECG-gated, black-blood prepared 2D phase-contrast sequence with three-directional velocity encoding (11,38–40) (VENC = 25 cm/s). Spatiotemporal imaging acceleration using Parallel MRI with Extended and Averaged GRAPPA Kernels (PEAK-GRAPPA) (41) with an undersampling factor of 5 permitted breath-hold data acquisitions with scan time = 24–28 heart beats per slice. Other relevant imaging parameters included: temporal resolution = 19–24 ms, in-plane spatial resolution = 2.0–2.3 mm², slice thickness = 8 mm, TE = 3.2–3.8 ms, TR = 4.8–6.1 ms, receiver bandwidth = 460–840 Hz/pixel, flip angle 10° or 15°.

Manual TPM Data Analysis

TPM data post-processing and myocardial velocity estimations were made using a custom-made software package programmed in MATLAB (The Mathworks Inc, Natick, Mass). First, the velocity data were pre-processed by correcting eddy currents (42) and bulk-motion (38,39,43). For manual segmentation, the magnitude images in short-axis views were used to place approximately 10–20 coordinate points, each for epicardial LV, endocardial LV, epicardial RV, and endocardial RV borders for the base, mid, and apex for all time frames, after which the software uses spline fitting to close the contour. The anterior and inferior LV-RV intersections were automatically detected for all time frames and used to remove the septum from the RV masks. The Cartesian velocity (V_x and V_y) within the segmented LV and RV masks were converted into velocities along the three principal directions of the heart - radial shortening (V_r), tangential/circumferential shortening (V_ϕ), and longitudinal shortening (V_z). For simplicity, only the V_r and V_z are considered for further statistical analyses. The expanded 16 LV +10 RV American Heart Association (AHA) model (44) was used to report segmental end-systolic and end-diastolic peak velocities. Global LV and RV peak velocities were obtained by averaging the segmental values for each ventricle. End-systole was detected automatically as the time frame with the smallest endocardial LV volume and end-diastole as the time frame with the largest LV volume (summed over all three slices). Analyzing each study manually from pre-processing to deriving velocities would take ~2 hours per patient with the most effort (95%) spent on manual placement of coordinate points.

Deep Learning Architecture

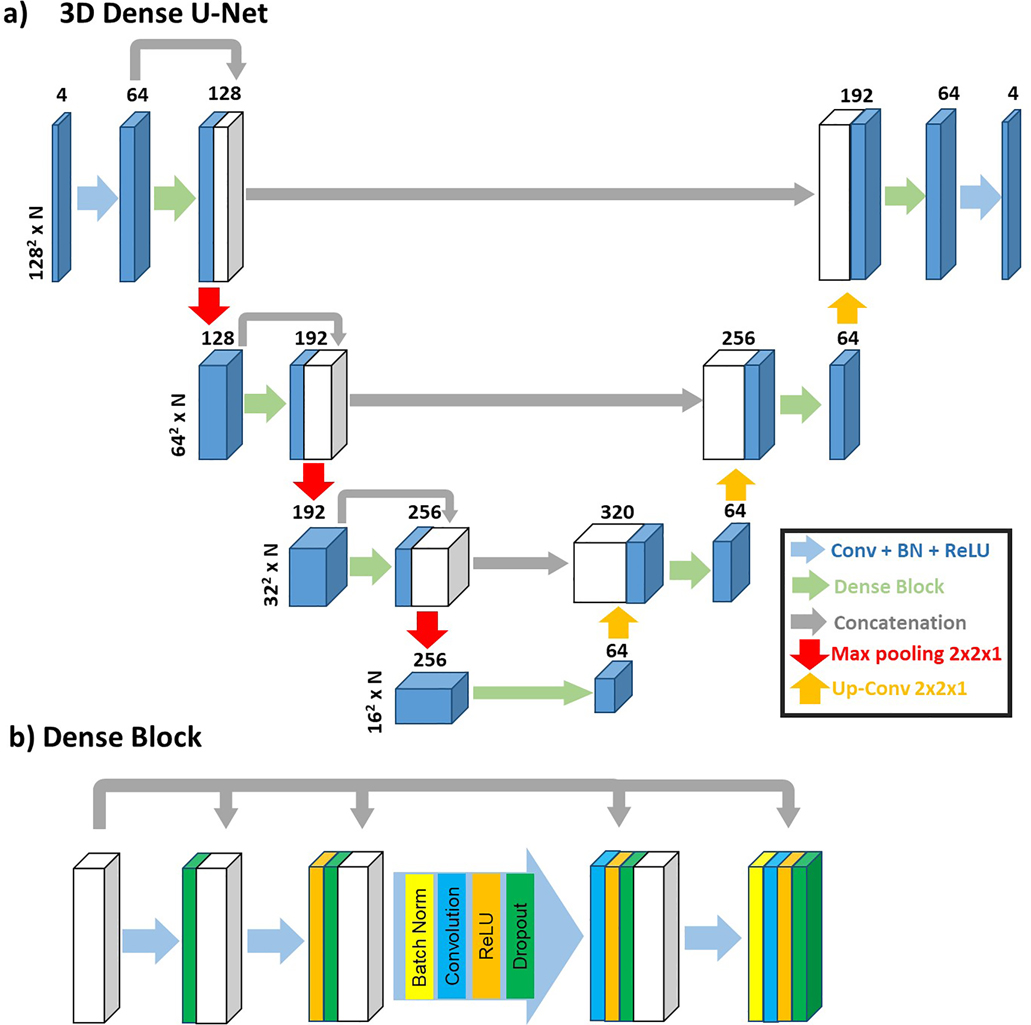
Consistent with prior studies (45,46), we have split our training and testing data to have approximately 3:1 ratio. For training, we randomly selected 114 scans (342 slices, 20–42 time frames per slice, 10,096 2D images) and for testing, the remaining 36 scans (108 slices, 23–36 time frames per slice, 3,288 2D images) were used. The pre-processed images after correction for eddy currents and bulk motion were used. While a fraction of image series (n=55 [12.6%] slices) had suboptimal image quality due to poor breath holding, we elected to include all image series in this study (n=39 [11.4%] for training; n=16 [14.8%] for testing.) As shown in Figure 1, the manual contours from three observers (AP, RS, AB; medical fellows with 2 to 8 years of experience) were transformed into multi-layer masks and used as the reference (i.e. labelled 0–3 for each pixel, 0: background, 1: blood pool, 2: RV myocardium, and 3: LV myocardium). A 3D (2D + time) dense U-Net (Figure 2) was used to learn the segmentation process, while 2D max pooling (2×2×1) was used to allow arbitrary number of time frames.

Figure 1.

The manual contours were transformed into multi-layer masks (i.e. 0 for background, 1 for blood pool, 2 for RV myocardium, and 3 for LV myocardium). We used the magnitude image and three dimensional velocity-encoded (V_x, V_y, V_z) images as independent input channels and the multi-class masks as the reference to train a 3D dense U-Net.

Figure 2.

a) A 3D (2D + time) Dense U-Net was used to learn the segmentation process, while max pooling (2×2×1) was used to allow arbitrary number (N) of time frames. b) The structure of dense block used in the 3D Dense U-Net.

Three different ways of utilizing the TPM images as inputs are compared: 1) magnitude image alone; 2) magnitude image and a combined velocity image ($V_{sum}=\sqrt{V_x^2+V_y^2+V_z^2}$); 3) magnitude and three dimensional velocity-encoded (V_x, V_y, V_z) images as independent input channels (i.e. stacked in the channel dimension). Input 3) was used for other comparisons.

For the loss term, in addition to cross-entropy loss, we investigated into multi-class dice loss (47), and Hausdorff distance (48) loss to achieve better results. For the dice loss, each class was calculated separately by Equation 1.

$$L_{DSC}=1-\frac{2\sum _i{s}_i{r}_i}{\sum _i{s}_i+\sum _i{r}_i}$$ Eq. 1,

where s_i is the DL segmentation result, and r_i is the ground truth at each voxel i. The dice losses of all three classes (i.e. blood pool, LV myocardium and RV myocardium) are weighted equally. The Hausdorff distance is calculated for the boundary of the entire segmentation (i.e. three classes combined). The total loss is described by Equation 2, where K is the total number of classes (i.e. 3) and ${L_{DSC}}_k$ is the dice loss for class k.

$$L_{total}=L_{CE}+\frac{1}{K}\sum _{k=1}^K{L_{DSC}}_k+L_{HD}$$ Eq. 2

Four different combinations of loss terms are compared: 1) L_CE alone; 2) L_CE + L_HD; 3) L_CE + L_DSC; 4) L_CE + L_DSC + L_HD. The loss terms were weighted equally in this study. Loss term 4) was used for other comparisons.

The training took 19.7 hours. As part of our efforts to ensure transparency and reproducibility, we have made available our dense U-Net architecture programmed in Pytorch (see the Data Availability Statement section). To check for overfitting, we performed a 5-fold cross validation experiment by repeating the training and testing as described above.

The DL-generated masks were converted into coordinate points and loaded onto the software for velocity estimations. Further analysis used the same semi-automatic procedure as for the manual analysis, interpolated splines were generated and LV-RV intersection points were identified.

Computer Hardware

For training and testing of the DL network, we used a GPU workstation (Tesla V100 32GB memory, NVIDIA, Santa Carla, California, USA; 32 Xeon E5–2620 v4 128 GB memory, Intel, Santa Clara, California, USA) equipped with Pytorch (Version 1.4, Berkeley Software Distribution), and MATLAB (R2020b, The Mathworks Inc, Natick, MA, USA) running on a Linux operating system (Ubuntu16.04).

Quantitative Analysis

To assess the accuracy of DL-based segmentation, we calculated the dice scores for LV and RV with manually contoured masks as reference. The Hausdorff distance is calculated for the entire heart segmentation to access the offsets of the boundaries. Peak-systolic and peak-diastolic LV and RV segmental velocities were compared between the manual segmentation and DL segmentation. A second independent observer (IO) manually analyzed 12 scans randomly selected from the 36 testing scans to evaluate inter-observer variability.

Statistical Analysis

The statistical analyses were conducted by two investigators (DS, AP) using MATLAB. We tested for normality of variables using the Shapiro-Wilk test. Normally distributed data were reported as mean ± standard deviation; non-normally distributed data were reported as median and interquartile range (IQR); 25^th percentile, 75^th percentile. Analysis of variance or Kruskal-Wallis test with Bonferroni correction were used to compare the quantitative metrics among different input groups and different loss term groups. Paired t-tests or Wilcoxon signed rank tests were used to compare the quantitative metrics between the manual and DL segmentations. Pearson correlation (r) and Bland Altman analyses were used to compare velocities derived from the manual and DL segmentations. A p < 0.05 was considered significant for each statistical test.

RESULTS

The mean segmentation time was approximately 2 hours per patient (3 slices per patient) for manual and 1.9 ± 0.3 seconds for DL segmentation. According to Shapiro-Wilk test, all three image quality metrics were not normally distributed (statistic = 0.874, p<0.001 for LV dice; statistic = 0.931, p <0.001 for RV dice; statistic = 0.895, p <0.001 for Hausdorff distance). Therefore, the Kruskal-Wallis and Wilcoxon signed rank tests were used to compare quantitative metrics.

Table S1 in Supplementary Materials summarizes the quantitative metrics measured on the 36 testing cases comparing the deep learning outcomes using different inputs. All three quantitative metrics were not significantly (p>0.37) different between the three groups. As shown in Figure S1, the magnitude + phase (V_x, V_y, V_z) as input produced better segmentation than other input cases, which contained noticeable discontinuity on LV or RV myocardium masks. Given that magnitude + phase (V_x, V_y, V_z) group produced better median quantitative metrics, we elected to use it throughout.

Table S2 in Supplementary Materials summarizes the quantitative comparison with different loss terms. While the LV and RV dice scores were not significantly (p>0.38) different among between four groups, the Hausdorff distance was significantly (p<0.03) different between the four groups. As shown in Figure S2 in Supplementary Materials, the CE + HD + Dice loss term produced better results than other loss terms. Thus, we elected to use it throughout.

As summarized in Table 1, the median dice scores for the LV and RV DL segmentations were 0.85 and 0.64, respectively. The median Hausdorff distance of the testing set is 3.17 pixels. As shown in Table 2, for the 12 scans including analyses by two observers, the dice score was significantly better for DL than the second independent observer for LV (DL: 0.86; manual IO: 0.80; p<0.001), but they were not significantly different for RV (DL: 0.62; second IO: 0.60; p=0.32). The median Hausdorff distance was not significantly different between DL and second IO (DL: 3.33 pixels; second IO: 3.58 pixels; p=0.23).

Table 1.

Summary of quantitative metrics of 36 testing cases comparing deep learning segmentation versus manual segmentation. Reported values represent median and 25^th to 75^th percentiles (parenthesis).

	LV Dice Score	RV Dice Score	Hausdorff Distance
Basal	0.84 (0.81–0.89)	0.69 (0.62–0.76)	3.19 (2.48–4.06)
Mid	0.85 (0.82–0.89)	0.67 (0.60–0.73)	2.93 (2.49–3.53)
Apex	0.84 (0.78–0.85)	0.46 (0.37–0.62)	3.59 (2.66–3.94)
Combined	0.85 (0.80–0.88)	0.64 (0.47–0.73)	3.17 (2.52–3.93)

Table 2.

Summary of quantitative metrics (dice and Hausdorff distance) of image quality from all 12 testing cases compared with second independent observer (IO) as reference. Reported values represent median and 25^th to 75^th percentiles (parenthesis).

	LV Dice Score		RV Dice Score		Hausdorff Distance
	DL	Second IO	DL	Second IO	DL	Second IO
Basal	0.88 (0.84–0.89)	0.80 (0.76–0.85)	0.73 (0.64–0.78)	0.70 (0.62–0.73)	2.81 (2.34–3.75)	3.14 (2.79–3.80)
Mid	0.86 (0.79–0.89)	0.80 (0.74–0.82)	0.67 (0.54–0.73)	0.64 (0.52–0.70)	3.04 (2.58–3.98)	3.11 (2.93–3.94)
Apex	0.83 (0.78–0.88)	0.74 (0.71–0.83)	0.39 (0.33–0.53)	0.38 (0.26–0.51)	3.82 (3.43–5.58)	4.36 (3.38–5.33)
Combined	0.86 (0.80–0.89)	0.80 (0.73–0.83)	0.62 (0.49–0.73)	0.60 (0.47–0.71)	3.33 (2.56–4.70)	3.58 (2.89–4.38)
P-value	<0.001		0.32		0.23

In the 5-fold cross validation experiment, all three quantitative metrics were not significantly (p>0.1) different among the five groups (see Table S3 in Supplementary Materials). Therefore, we used the first experiment results throughout.

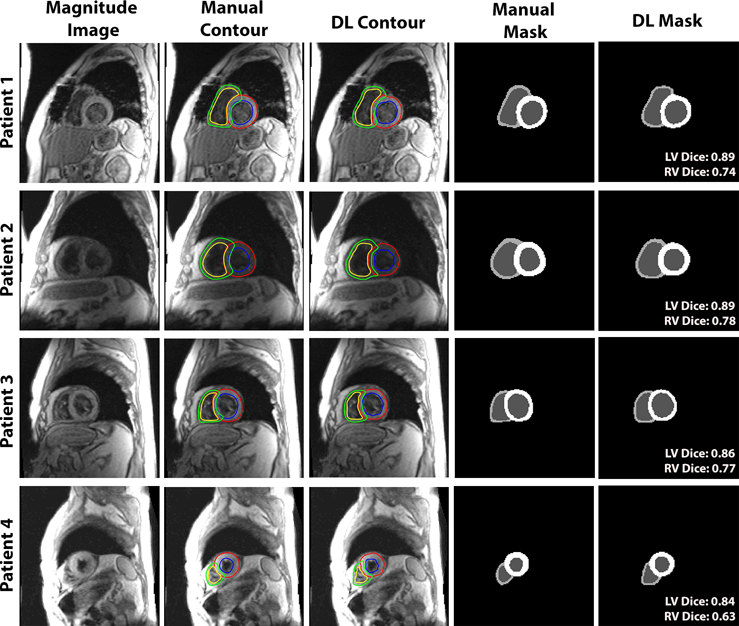
Figure 3 shows four representative cases of TPM segmentation using manual contouring and deep learning. These example results show good agreement between manual and DL segmentation. For dynamic display of Figure 3, see Video S1 in Supplemental Materials. Figure 4 shows example V_r and V_z time curves of LV and RV for manual and DL contours on the right and the corresponding velocity maps at end-systolic and end diastolic time frames on the left. This example shows good agreement in time-resolved velocity measurements derived from manual and DL segmentation. For dynamic display of Figure 4, see Video S2 in Supplemental Materials.

Figure 3.

Four representative patients comparing manual and DL segmentations. (Left column) The magnitude image; color-coded contours produced by manual (second column) and DL (third column): LV epicardium (red), LV endocardium (blue), RV epicardium (green) and RV endocardium (yellow). (4^th and 5^th column from the left) The multi-layer masks produced by manual (fourth column) and DL (fifth column). The dice scores of LV and RV myocardium for each case are labeled on the lower right corner of the DL masks.

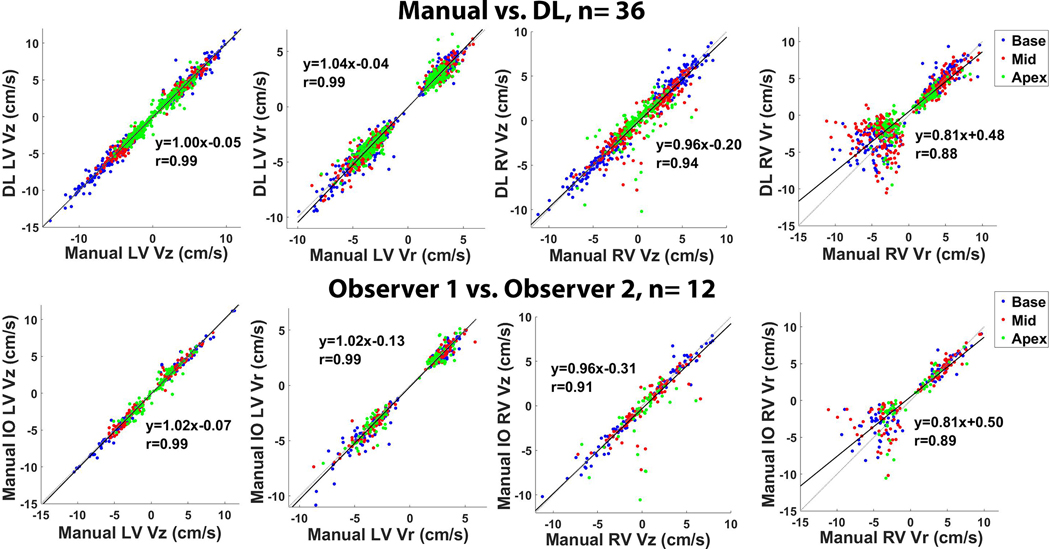
Figure 4.

Linear regression plots illustrating strong correlation between segmentation methods (top row, manual vs. DL, 36 testing cases, R ≥ 0.88) and between independent observers (bottom row, 12 manual IO cases, R ≥ 0.88) for peak V_r and V_z (LV and RV, systole and diastole). All 26 segments are plotted with the basal, mid-ventricular, and apical segments color-coded as red, blue and green, respectively.

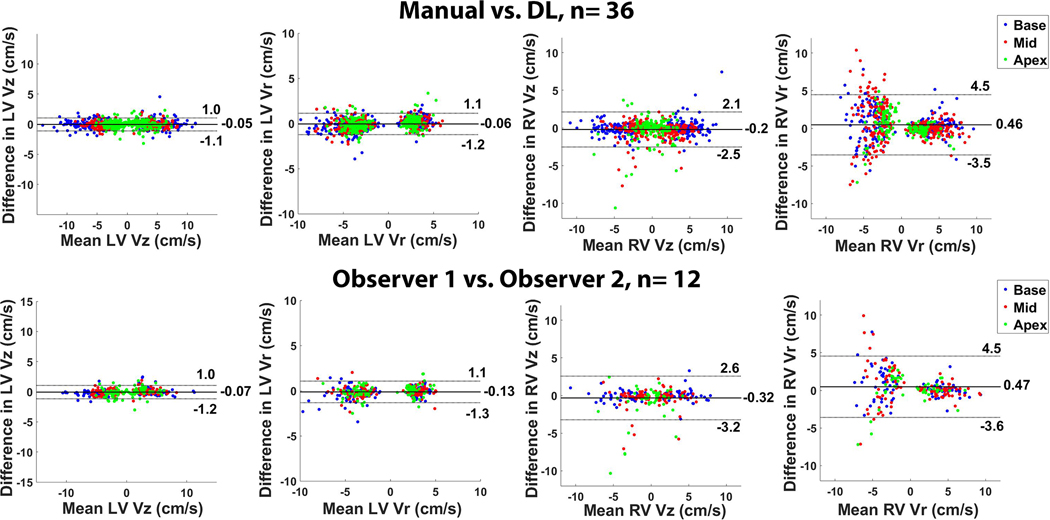
Figure 5 shows scatter plots resulting from linear regression analysis illustrating strong correlation between manual and DL segmentation methods (R ≥ 0.88) and between two independent observers (R ≥ 0.89) for peak V_r and V_z (LV and RV, systole and diastole). All 26 segments (LV and RV 16+10 segment AHA model) are plotted with the basal, mid-ventricular, and apical segments color-coded as red, blue and green, respectively. Figure 6 shows Bland-Altman plots illustrating good agreement between manual and DL segmentation for LV V_z (mean = 3.85 cm/s; mean difference = −0.05 cm/s (1.3 % of mean); the upper and lower limits of agreement [LOA] = −0.05 ± 0.98 cm/s); LV V_r (mean = 3.38 cm/s; mean difference = −0.06 cm/s (1.8% of mean); and the upper and lower LOA = −0.06 ± 1.18 cm/s); RV V_z (mean = 2.96 cm/s; mean difference = −0.21 cm/s (7.1% of mean); and the upper and lower LOA = −0.21 ± 2.33 cm/s); RV V_r (mean = 3.95 cm/s; mean difference = 0.46 cm/s (11.7% of mean); and the upper and lower LOA = 0.46 ± 4.00 cm/s).

Figure 5.

Bland-Altman plots illustrating good agreement between segmentation methods (top row, manual vs. DL, 36 testing cases) and between independent observers (bottom row, 12 manual IO cases) for peak V_r and V_z (LV and RV, systole and diastole). All 26 segments are plotted with the basal, mid-ventricular, and apical segments color-coded as red, blue and green, respectively.

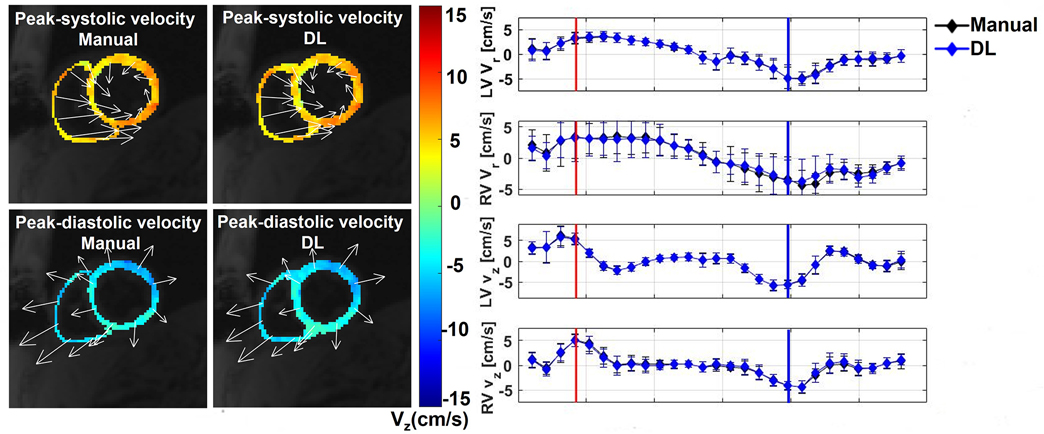
Figure 6.

(Left) Biventricular velocity maps derived from manual and DL segmentations at the peak-systolic and peak-diastolic time frames. Myocardial longitudinal velocities are color-coded and in-plane velocities are depicted by regionally averaged velocity vectors. (Right) Time resolved V_r and V_z curves of LV and RV. The red and blue vertical lines represent the time frames shown on the left (peak-systole and peak-diastole), while the black and blue curves represent manual and DL contours, respectively, with each time-frame represented by a rhombus.

Figure 6 also shows good agreement between independent observers for LV V_z (mean = 3.54 cm/s; mean difference = −0.07 cm/s (2.0% of mean); and the upper and lower LOA = −0.07 ± 1.10 cm/s); LV V_r (mean = 3.33 cm/s, mean difference = −0.13 cm/s (3.9% of mean); and the upper and lower LOA = −0.13 ± 1.21 cm/s); RV V_z (mean = 2.82; mean difference = −0.32 cm/s (11.4% of mean); and the upper and lower LOA = −0.32 ± 2.92 cm/s); RV V_r (mean = 4.11 cm/s; mean difference = 0.47 cm/s (11.4% of mean); and LOA = 0.47 ± 4.06 cm/s).

DISCUSSION

This study describes the implementation and evaluation of a DL-based automated image segmentation method for TPM images. As expected, the processing time is 3,600-times shorter for DL (~2 s) than manual segmentation (~7,200 s). The resulting accuracy (LV dice = 0.85, RV dice = 0.64, Hausdorff distance = 3.17 pixels) in segmentation with DL was slightly better than inter-observer agreement (LV dice = 0.80, RV dice = 0.60, Hausdorff distance = 3.58 pixels).

This study has several points that warrant further explanations. First, we used a 3D dense U-Net architecture in this study. Compared to a traditional convolution layer with increasing channel sizes in the deeper layers, the dense layer uses a series of convolutions of relatively small sized channels (i.e. 16) and concatenates the feature maps from previous convolutions (49,50). This largely reduces the overall number of parameters (3D U-Net: 18.8M, ours: 2.7M) by efficiently utilizing every feature extracted throughout the CNN, thereby reducing the significant computational demand (e.g. GPU memory) for 3D CNNs (51–53). Second, by utilizing the magnitude and phase (V_x, V_y, V_z) images together, the dense U-Net produced better results than using magnitude alone (see Figure S1 and Video S3 in Supplementary Materials). Previously, our team found similar results in a cohort of 26 pulmonary hypertension patients and 8 healthy controls (54). A 4-channel network using the magnitude and 3 phase images together showed better results than a 1-channel network using only the magnitude images and a 2-channel network using the magnitude and a combined velocity ($V_{sum}=\sqrt{V_x^2+V_y^2+V_z^2}$). While the phase images are hard to be used by human, they can be utilized to enrich the image features learned by DL networks, thereby improve the performance of DL networks. Third, incorporating cross-entropy loss, dice loss and Hausdorff distance into the loss function produced better results (see Figure S2 and Video S4 in Supplementary Materials). Forth, the dice scores were significantly better for DL than second IO for LV (DL: 0.86; second IO: 0.80; p<0.001) but not for RV (DL: 0.62; second IO: 0.60; p=0.49). For more accurate segmentation, DL results can be used as an initial guess and then further improved with minor manual adjustments, at the expense of increased processing time. This semi-automated method may still be fast enough for clinical translation of TPM.

DL-based RV myocardial segmentation is challenging due to its complex crescent shape that varies across slices and phases. The inhomogeneity in shape and myocardial signal intensity in our cohort of post-cardiac transplant subjects adds to this problem. Previous works on RV myocardial segmentation are limited. The finalists of the MICCAI 2012 Right Ventricle Segmentation Challenge used either automated or semi-automated approaches, three of which are atlas-based methods, two are prior-based methods, and two are prior-free, image-driven methods that make use of the temporal dimension of the data (55). An end-to-end DL-based CNN architecture was implemented by Tran et al. to segment the LV and RV myocardium from short-axis cine slices (56). All of these prior works were conducted using cine CMR images, which have a high blood-to-myocardial contrast. A future work is warranted to improve the RV segmentation performance in TPM images.

This study has several limitations that warrant further discussion. First, we did not document the manual segmentation time from prior analysis. For this study, one observer (AS) with prior experience with TPM analysis repeated the analysis for three training datasets to derive an approximate segmentation time of 2 hours per patient. Second, the DL segmentation results may be influenced by poor image quality (i.e. image artifacts caused by breathing motion, metals), whereas manual contours is less sensitive to artifacts because trained observers may use prior knowledge to over read poor image quality. One approach to improve DL based segmentation is by incorporating shape models. Third, as shown in Figure 6, the agreement in Vz and Vr was significantly worse for RV than LV. This may be due to: 1) partial volume averaging, as the RV myocardium is thinner than the LV; 2) susceptibility artifact from open chest surgery (i.e. signal void caused by sternal wires), which is closer to the RV; 3) epicardial fat signal, which makes it harder to determine epicardial RV boundary. The agreement in Vr for RV was worse for diastole with negative velocities than systole with positive velocities. This may be due to: 1) partial volume averaging, as the RV is thinner at diastole than systole; 2) proximity to signal void caused by sternal wires, which is closer at diastole than systole. Fourth, we did not compare our DL-based method to previously published semi-automated or automated methods for TPM (24–27) due to lack of access to such methods. A future study is warranted to conduct a head-to-head comparison for segmentation accuracy and computational efficiency. Fifth, this study used data obtained from a single site, scanner vendor, and field strength, which may limit generalizability to other sites, scanner vendors and field strengths. Sixth, we used equal weight for the different loss terms in this study. A future study is warranted to determine the optimal weight for each loss term to achieve best results.

In summary, this study describes an automated image segmentation method for biventricular TPM images with deep learning that is significantly faster than manual contouring, without significant loss in segmentation accuracy and TPM parameters, thereby verifying clinical translatability.

Supplementary Material

Video S3

Supplementary Video S3. Dynamic display of results for 3 groups with different inputs to the network shown in Figure S1.

Video S4

Supplementary Video S4. Dynamic display of results for 4 groups with different loss terms shown in Figure S2.

Video S2

Supplementary Video S2. Dynamic display of biventricular velocity maps derived from manual and DL segmentations at the peak-systolic and peak-diastolic time frames shown in Figure 6.

Supplemental Tables and Figures

Figure S1. Examples of results for 3 different input to the network with the same loss term (CE+HD+Dice): 1) magnitude image alone; 2) magnitude image and a combined velocity ($V_{sum}=\sqrt{V_x^2+V_y^2+V_z^2}$); 3) magnitude and phase (V_x, V_y, V_z) images. The group with magnitude and phase images as input showed qualitatively better results than the other groups. For dynamic display, see Video S3.

Figure S2. Examples of results for 4 different loss terms with the same input (Magnitude and phase) images: 1) cross-entropy (CE) loss; 2) CE and Hausdorff distance (HD) loss; 3) CE and multi-class dice loss; and 4) CE, HD and dice loss all combined. The group with CE, HD and dice loss combined showed qualitatively better results than the other groups. For dynamic display, see Video S3.

Table S1: Summary of quantitative metrics of 36 testing cases comparing deep learning segmentation using different inputs with manual segmentation as reference: 1) magnitude image alone; 2) magnitude image and a combined velocity ($V_{sum}=\sqrt{V_x^2+V_y^2+V_z^2}$); 3) magnitude and phase (V_x, V_y, V_z) images. Reported values represent median and 25th to 75th percentiles (parenthesis).

Table S2: Summary of quantitative metrics of 36 testing cases comparing deep learning segmentation using different loss terms with manual segmentation as reference: 1) cross-entropy (CE) loss; 2) CE and Hausdorff distance (HD) loss; 3) CE and multi-class dice loss; and 4) CE, HD and dice loss all combined. Reported values represent median and 25th to 75th percentiles (parenthesis).

Table S3: Summary of quantitative metrics of the 5-fold cross validation. All 150 scans were randomly split into 5 groups, the training and testing were performed 5 times with each group as testing set and the rest 4 groups as training set. Reported values represent median and 25th to 75th percentiles (parenthesis).

List of Abbreviations

AHA

American Heart Association

CMR

Cardiovascular Magnetic Resonance

DENSE

Displacement-Encoded imaging with Stimulated Echoes

DL

Deep Learning

DICOM

Digital Imaging and Communications in Medicine

ECV

Extracellular Volume

FOV

Field of View

GPU

Graphic Processing Unit

HIPAA

Health Insurance Portability and Accountability Act

HTx

Heart Transplant

LOA

Limits of Agreement

LV

Left Ventricular

IO

Independent Observer

RV

Right Ventricular

SENC

Strain-Encoded

SNR

Signal-to-Noise-Ratio

TPM

Tissue Phase Mapping

Data Availability Statement

The Pytorch codes used for implementing our dense U-Net can be found in GitHub (https://github.com/dsc936/DenseUnet_for_TPM_segmentation).