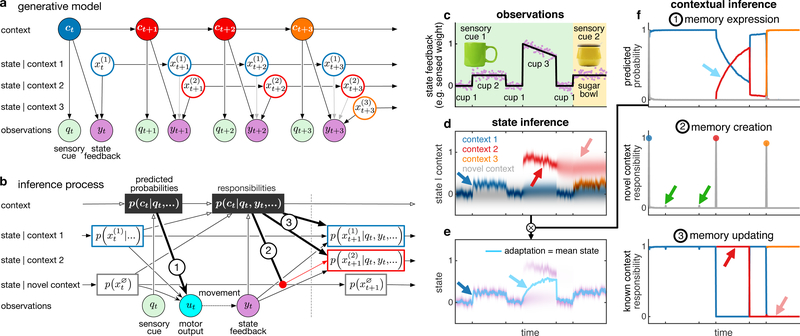
Fig. 1 |. Contributions of contextual inference to motor learning in the COIN model.

a, Generative model. A (potentially) infinite number of discrete contexts c_t (colours) exist that transition as a Markov process. Each context j is associated with a time-varying state $x_t^{(j)}$. The active context can generate a sensory cue q_t independent of movement (e.g. the visual appearance of an object) and also determines which state is observed (with noise) as state feedback y_t as a consequence of movement (e.g. object weight, black vs. grey arrows). b, Inference process. The learner infers contexts and states (and parameters, not shown) based on observed sensory cues and state feedback. Before movement, predicted context probabilities p(c_t | q_t,…) are computed by fusing prior expectations from the previous time point (where … refers to all observations before time t) with the likelihood of the current sensory cue q_t. For each known context, a predicted distribution over its current state $p(x_t^{(j)}\mid \dots )$ is represented. A potential novel context is always represented, with a stationary state distribution $p(x_t^{\varnothing })$. Motor output u_t is the average of the states of the known and novel contexts, weighted by their predicted probabilities (arrow 1). Movement results in state feedback y_t, which updates the predicted context probabilities to context responsibilities p(c_t | q_t, y_t,…). A new memory is instantiated with a probability that is the responsibility of the novel context (arrow 2, showing the creation of a red context, initialised as a copy of the state distribution of the novel context). Responsibilities also determine the degree to which state feedback is used to update the predicted state distribution $p(x_{t+1}^{(j)}\mid q_t,y_t,\dots )$ of each context (arrows 3). c, Simulated time series of sensory cues (background colour for object appearance) and state feedback observations (noisy weight, purple) when handling visually-identical cups and a sugar bowl of varying weights (black line, arbitrary scale). The weight of cup 3 decreases as liquid is poured from it, other objects have constant weights. (d-f) The COIN model applied to the observations in c. d, Predicted state distributions for the three contexts inferred by the model and a novel context. e, The predicted state distribution (purple) is a mixture of the individual contexts’ predicted state distributions (d) weighted by their predicted probabilities (f₁). The motor output (adaptation, cyan line) is the mean of the predicted state distribution. Intensity of colours in d and purple in e indicates probability density, linearly scaled between 0 and the maximum of the corresponding density. f, Contextual inferences (colours as in d). 1. Predicted probability (before state feedback) of each known context and a novel context. 2. Responsibility (context probability after state feedback) of a novel context. Coloured circles show memory creation events. The novel context responsibility is insufficient to generate a new memory when transitioning to and from cup 2 (green arrows). 3. Responsibility of each known context. See text for arrow explanations in d-f.