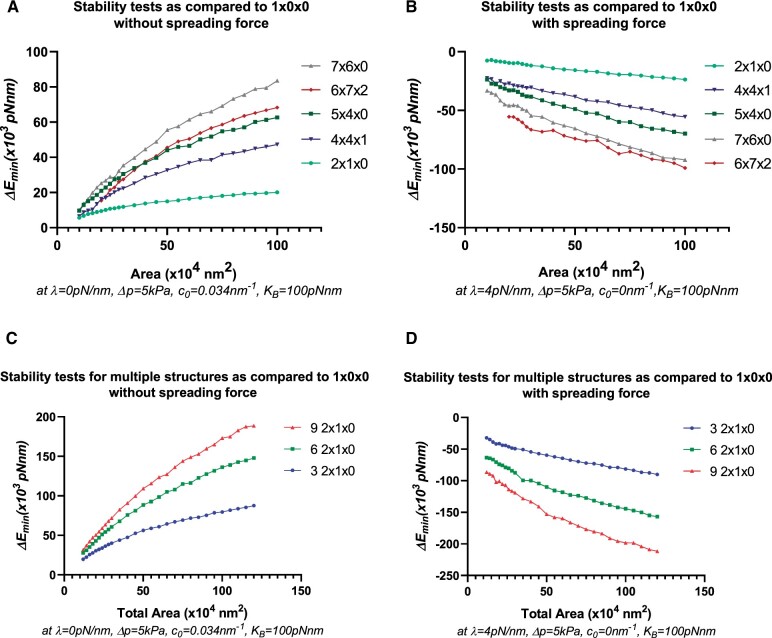
Figure 3.

Stability tests to determine the role of a spreading force in different shape conformations. A and B, Stability tests determined by $\mathrm{\Delta }{E}_{\min }$ versus Area for different conformations compared to a single oblate spheroid at the labelled area. A positive value of $\mathrm{\Delta }{E}_{\min }$ indicates relative stability of the labelled conformation as compared to a single oblate spheroid (1 × 0 × 0). A, Relative stability of tubular (2 × 1 × 0, 5 ×4 × 0, 7 × 6× 0) and fenestrated (4 × 4 × 1, 6 × 7 × 2) structures in the absence of a spreading force with a finite spontaneous curvature. B, Stability of a single oblate spheroid over tubular and fenestrated structures in the presence of a spreading force and with zero spontaneous curvature. Note that in (B) a decrease of spontaneous curvature to a threshold value close to 0.015 $\mathrm{n}{\mathrm{m}}^{-1}$yields similar results. C and D, Stability test for multiple 2 × 1 × 0 structures compared to a single oblate spheroid at the labeled area. C, Relative stability of multiple 2 × 1 × 0 structures compared to a single oblate spheroid in the absence of a spreading force. At a labeled area, a larger number of structures have collectively a higher, more positive value of $\mathrm{\Delta }{E}_{\min }$, thereby indicating that in the absence of a spreading force, tubular, as well as emerging fenestrated/network structures (as inferred by the results of A and B) are energetically favorable and tend to accumulate as shown in Figure  1G. D, Stability of a single oblate spheroid compared to multiple 2 × 1 × 0 structures in the presence of a spreading force and with zero spontaneous curvature. In the presence of a spreading force, at a labeled area, a larger number of structures have a lower, more negative value of $\mathrm{\Delta }{E}_{\min }$ collectively, thereby indicating the energetic favorability of structures fusing to form larger, more mature structure(s).