SpeciesRax: A Tool for Maximum Likelihood Species Tree Inference from Gene Family Trees under Duplication, Transfer, and Loss

Abstract

Species tree inference from gene family trees is becoming increasingly popular because it can account for discordance between the species tree and the corresponding gene family trees. In particular, methods that can account for multiple-copy gene families exhibit potential to leverage paralogy as informative signal. At present, there does not exist any widely adopted inference method for this purpose. Here, we present SpeciesRax, the first maximum likelihood method that can infer a rooted species tree from a set of gene family trees and can account for gene duplication, loss, and transfer events. By explicitly modeling events by which gene trees can depart from the species tree, SpeciesRax leverages the phylogenetic rooting signal in gene trees. SpeciesRax infers species tree branch lengths in units of expected substitutions per site and branch support values via paralogy-aware quartets extracted from the gene family trees. Using both empirical and simulated data sets we show that SpeciesRax is at least as accurate as the best competing methods while being one order of magnitude faster on large data sets at the same time. We used SpeciesRax to infer a biologically plausible rooted phylogeny of the vertebrates comprising 188 species from 31,612 gene families in 1 h using 40 cores. SpeciesRax is available under GNU GPL at https://github.com/BenoitMorel/GeneRax and on BioConda.

Introduction

Species tree inference is a challenging fundamental problem in evolutionary biology. Species trees provide a framework for interpreting biological diversity, determining evolutionary relationships, studying the evolution of key traits, and for understanding the underlying processes of evolution. But existing methods for species tree inference have widely appreciated limitations (Dagan and Martin 2006; Bryant and Hahn 2020). New methods that can make better use of genome-scale data, including multicopy gene families, resolve long-standing debates about challenging nodes in the tree of life and the processes of genome evolution that underpin major transitions in evolution.

Perhaps, the most widely used approach for species tree inference is concatenation (also known as the supermatrix approach). Here, per-gene sequences are first aligned into per-gene multiple sequence alignments (MSAs) and subsequently concatenated into a single, large supermatrix. Then, statistical tree inference methods (maximum likelihood [Kozlov et al. 2019; Minh et al. 2020] or Bayesian inference [Aberer et al. 2014; Lartillot et al. 2009; Ronquist et al. 2012]) are applied to infer a tree on these supermatrices. The concatenation approach heavily depends on accurate orthology inference, which still constitutes a challenging problem (Altenhoff et al. 2019). In addition, concatenation methods were shown to be statically inconsistent under the multispecies coalescent model (Kubatko and Degnan 2007; Mendes and Hahn 2018) because of potential incomplete lineage sorting (ILS). Furthermore, supermatrix analyses can be misled in unpredictable ways if horizontal gene transfers (HGTs) are included in the concatenated supermatrix, for instance when analyzing microbial data (Williams and Embley 2014; Dombrowski et al. 2020). Hybridization (Elworth et al. 2019; Lutteropp et al. 2021), and recombination (Posada 2000) constitute other sources of incongruence between the species tree and the per-gene sequences that might cause the supermatrix approach to fail.

As gene family tree (GFT) methods can alleviate some of the pitfalls of the supermatrix approach, they are becoming increasingly popular. GFT methods can take into account that the evolutionary histories of the gene trees and the species tree are discordant due to biological phenomena such as ILS, gene duplication, gene loss, and HGT. In addition, some GFT methods can estimate the root of the species tree without the need for an outgroup. Character evolution tracing or phylogenetic post analysis methods such as dating or species delimitation require a rooted tree as input, to identify ancestor–descendant relationships. But inferring the root can be difficult using the standard outgroup method when the outgroup is distant or when no obvious outgroup is available (Shavit et al. 2007).

At present, the most widely used GFT tools only model ILS (Bouckaert et al. 2014; Zhang et al. 2018) and are limited to single-copy gene families. Several tools that can handle multicopy gene families have been developed (Wehe et al. 2008; Boussau et al. 2012; Zhang et al. 2020; Molloy and Warnow 2020), but, despite the potential of these approaches, they have not yet been widely adopted. This may be due to the unfamiliarity of the software and, for some tools, the lack of an efficient, scalable, and user-friendly approach. This situation is beginning to change: ASTRAL-Pro can deal with duplications and losses, and SpeciesRax—the tool we introduce here—can account for duplications, losses and transfers, which may be particularly important in the analysis of microbial genomes.

One class of existing methods to infer species trees from multiple-copy gene families attempts to simultaneously estimate the GFTs and the species tree (Boussau et al. 2012; de Oliveira Martins and Posada 2017). However, these methods are computationally demanding and are limited to small data sets comprising less than 100 species.

Another class of existing methods handles the GFT inference and the species tree inference steps separately. As input they require a set of given, fixed GFTs and do not attempt to correct the GFTs during the species tree inference step. DupTree (Wehe et al. 2008) and DynaDUP (Bayzid et al. 2013) search for the species tree with the most parsimonious reconciliation cost, measured as the number of duplication events in DupTree, and the sum of duplication and loss events in DynaDUP. STAG (Emms and Kelly 2018) infers a species tree by applying a distance method to each gene family that covers all species, and subsequently builds a consensus tree from all these distance-based trees. However, STAG ignores a substantial fraction of signal by discarding gene families that do not cover all species. FastMulRFS (Molloy and Warnow 2020) extends the definition of the Robinson–Foulds (RF) distance to multiple-copy GFTs and strives to minimize this distance between the species tree and all input GFTs. ASTRAL-Pro (Zhang et al. 2020) is a promising improvement of ASTRAL that can handle multiple-copy GFTs: ASTRAL-Pro uses dynamic programming to infer the species tree that maximizes a novel measure of quartet similarity that accounts for orthology as well as paralogy. All of the above methods are nonparametric and do not deploy a probabilistic model of evolution. In addition, none of them explicitly models HGT.

Here, we present SpeciesRax, the first maximum likelihood method for inferring a rooted species tree from a set of GFTs in the presence of gene duplication, gene loss, and HGT. We implemented it in the GeneRax framework, our recently published species-tree-aware GFT correction tool (Morel et al. 2020). SpeciesRax takes as input a set of MSAs and/or a set of GFTs. If MSAs are provided, SpeciesRax will infer one maximum likelihood GFT tree per gene family using RAxML-NG (Kozlov et al. 2019). Thereafter, SpeciesRax first generates an initial, reasonable (i.e., nonrandom) species tree by applying MiniNJ (which we also introduce in this paper), our novel distance-based method for species tree inference from GFTs in the presence of paralogy. MiniNJ shows similar accuracy as other nonparametric methods while being at least two orders of magnitude faster on large data sets. Finally, SpeciesRax executes a maximum likelihood tree search heuristic under an explicit statistical gene loss, gene duplication, and HGT model starting from the MiniNJ species tree. When the species tree search terminates, SpeciesRax calculates approximate branch lengths in units of mean expected substitutions per site. Furthermore, it quantifies the reconstruction uncertainty by computing novel quartet-based branch support scores on the species tree. Because we implemented all of these new methods in our GeneRax software, users can now perform GFT inference, species tree inference, GFT correction, and GFT reconciliation with the species tree using a single tool. We show that SpeciesRax is fast and at least as accurate as the best competing species tree inference tools. In particular, SpeciesRax is twice as accurate (in terms of relative RF distance to the true species trees) than all other tested methods on simulations with large numbers of paralogous genes.

Results

Accuracy on Simphy Simulations

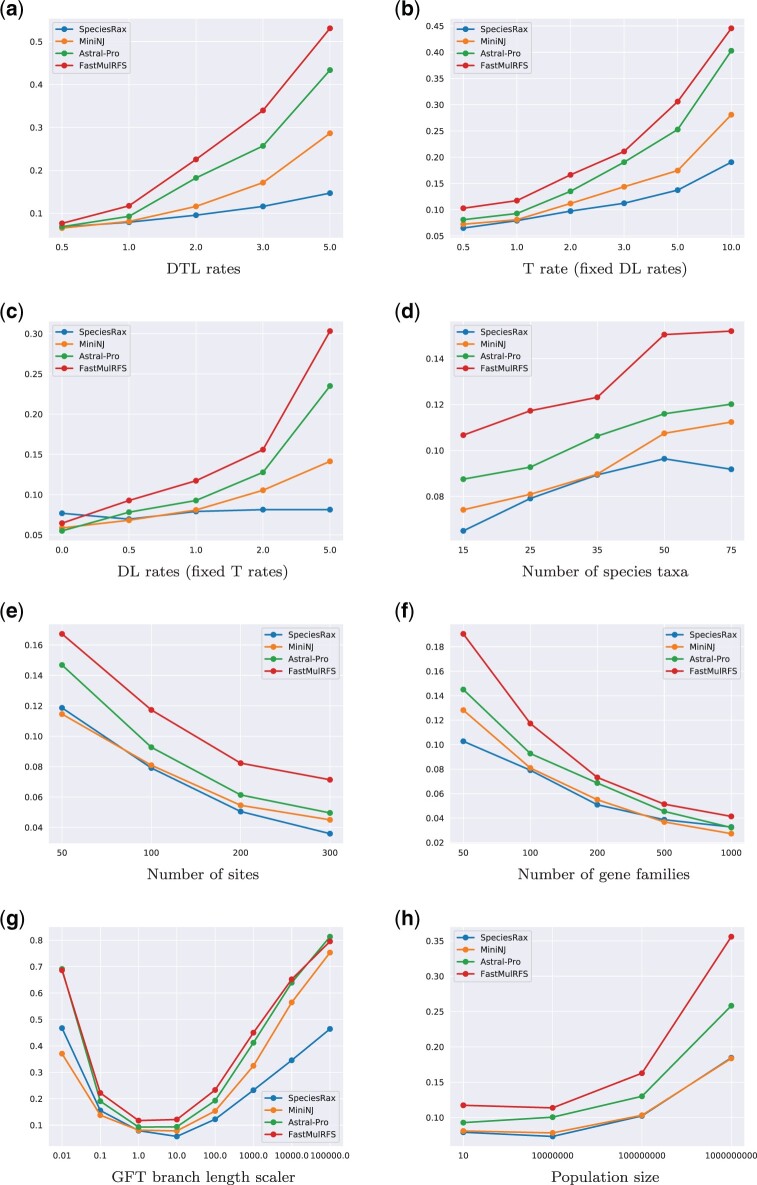
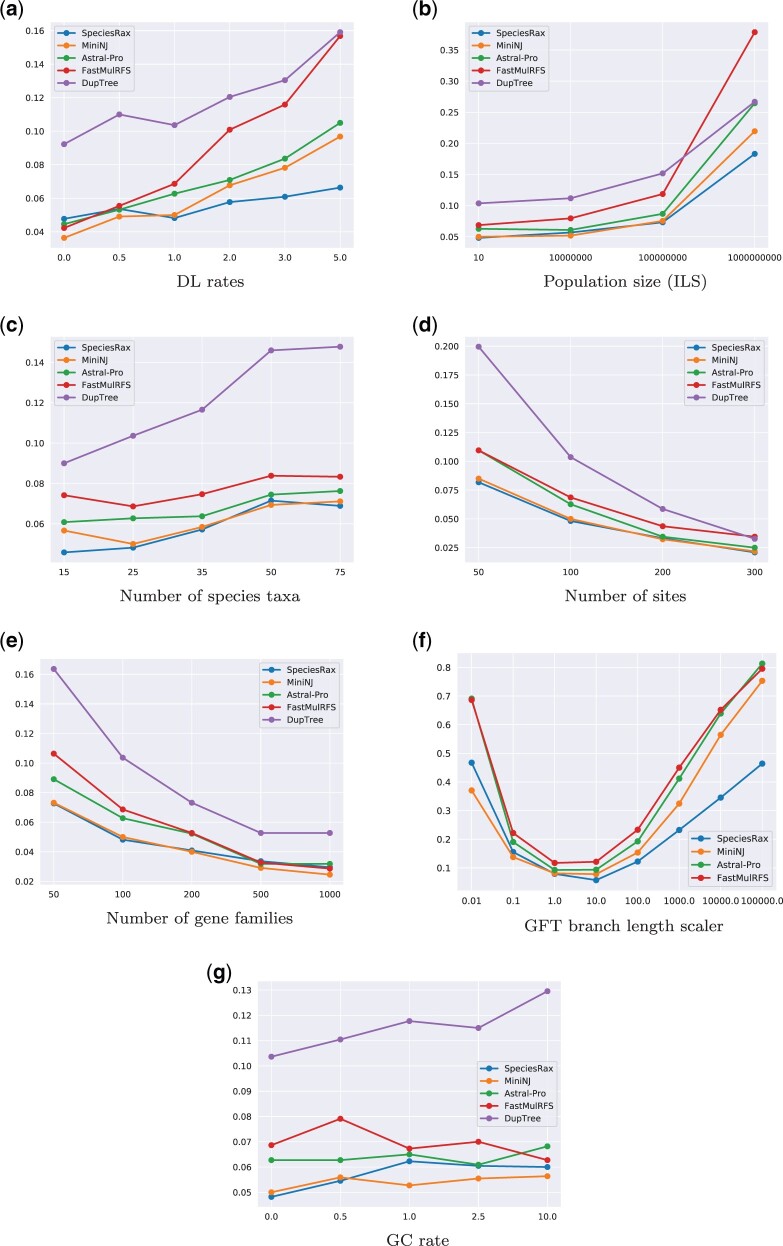
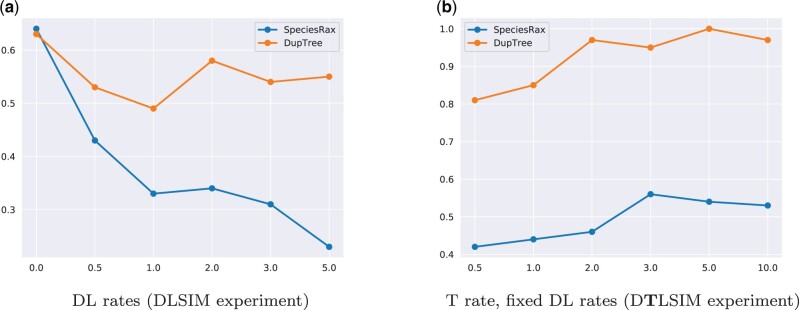
We plot the accuracy of the different species tree reconstruction methods under varying parameters for the D TLSIM and DLSIM experiments in figures 1 and 2, respectively. We excluded DupTree and NJst from the D TLSIM plots and NJst from the DLSIM plots for the sake of an improved visual representation of the results because of their very high error rate. In addition, we represent the average relative RF distance of all tested methods over all simulated data sets in table 1. For species trees with 25 taxa, one incorrect split corresponds to a relative RF distance of 0.045.

Fig. 1.

Average unrooted RF distance between inferred and true species trees, in the presence of duplication, loss, and HGT. (a) DTL rates, (b) T rate (fixed DL rates), (c) DL rates (fixed T rates), (d) number of species taxa, (e) number of sites, (f) number of gene families, (g) GFT branch length scaler, and (h) population size.

Fig. 2.

Average unrooted RF distance between inferred and true species trees, in the presence of duplication and loss (no HGT). (a) DL rates, (b) population size (ILS), (c) number of species taxa, (d) number of sites, (e) number of gene families, (f) GFT branch length scaler, and (g) GC rate.

Table 1.

Average Relative RF Distance between the Inferred Trees and the True Trees Over All Simulated Data Sets.

Method	D TLSIM	DLSIM
SpeciesRax	0.110	0.092
MiniNJ	0.132	0.099
ASTRAL-Pro	0.172	0.121
FastMulRFS	0.202	0.133
DupTree	0.518	0.212
NJst	0.455	0.346

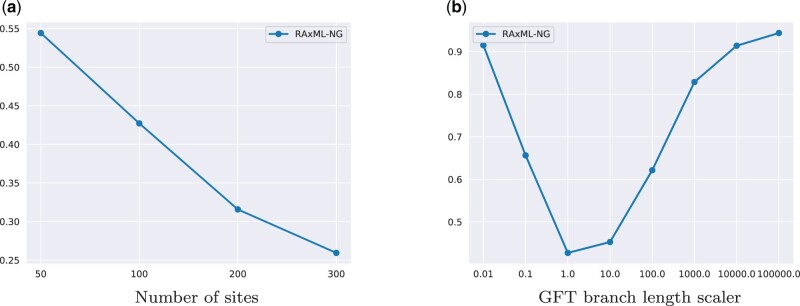
We also assessed the accuracy of the reconstructed GFTs under different simulation parameter configurations. Under the default parameters, the average relative RF distance between the true GFTs and the GFTs inferred with RAxML-NG is 0.43 for the D TLSIM and DLSIM experiments. When varying the number of sites, the average relative RF distance ranges between 0.26 for 300 sites and up to 0.54 for 50 sites (see fig. 3a). When varying the GFT branch length scaler, the average RF distance varies from 0.42 without scaling to 0.91 for the smallest scaling value of 0.01 and 0.94 for the largest scaling value of 100,000 (see fig. 3b). The remaining simulation parameters do not have a substantial impact on the GFT inference accuracy.

Fig. 3.

Average relative average distance between true and inferred GFTs on simulated data sets (SIMDL experiment). (a) Number of sites and (b) GFT branch length scaler.

Table 1 shows that SpeciesRax is on average the most accurate method, followed by MiniNJ, ASTRAL-Pro, and FastMulRFS. DupTree and NJst are substantially less accurate than SpeciesRax (by a factor of 4 up to 5 in presence of HGT) and all aforementioned methods.

As expected, all methods perform better when the degree of informative data (number of sites, number of families) increases and perform worse when the discordance between the GFTs and the species tree (ILS level, DTL rates) increases. We do not observe a clear correlation between the number of species and the reconstruction accuracy.

Compared with the other methods, SpeciesRax reconstruction accuracy seems to be less affected by increasing DTL rates and almost unaffected by increasing DL rates. We hypothesize that high DL rates are more likely to introduce adversarial (or hidden) paralogy. In other words, paralogous genes are likely to be labeled as orthologous genes by approaches such as ASTRAL-Pro or FastMulRFS that only infer paralogy from the GFTs (see also Molloy and Warnow 2020). For instance, FastMulRFS has only been proven to be consistent when no adversarial paralogy occurs (Molloy and Warnow 2020). In addition, ASTRAL-Pro and FastMulRFS do not attempt to handle HGT events. SpeciesRax explicitly models both, DL, and HGT events, which might explain why it is more robust to both, adversarial paralogy, and HGT.

Large ancestral population sizes are associated with higher rates of ILS. As SpeciesRax does not explicitly model ILS, it might be expected to perform poorly as the rate of ILS increases. In our simulations, all methods performed worse as the ancestral population size was increased, but the reduction in accuracy was similar for SpeciesRax and for methods that account for ILS.

For instance, in the DLSIM experiment, for a moderate population size (10⁷ individuals), SpeciesRax, MiniNJ, and ASTRAL-Pro exhibit analogous accuracy (rRF = 0.057, rRF = 0.052, and rRF = 0.061, respectively). Under the largest simulated population size (10⁹ individuals), SpeciesRax (rRF = 0.183) outperforms MiniNJ (rRF = 0.219), ASTRAL-Pro (rRF = 0.264), DupTree (rRF = 0.266), and FastMulRFS (rRF = 0.379).

Finally, increasing gene conversion (GC) rates does not seem to substantially affect the accuracy of the competing methods.

Accuracy on Empirical Data Sets

Here, we describe the results of species tree inference on empirical data sets with ASTRAL-Pro, DupTree, FastMulRFS, MiniNJ, and SpeciesRax. We excluded NJst from this analysis because it performed poorly on most empirical data sets. Initially, we only compare unrooted topologies and defer the root placement analysis to a separate subsection. We provide a graphical representation of the species trees inferred with SpeciesRax as well as the relative pairwise RF distances between all pairs of inferred trees in Supplementary Material online.

Vertebrates188 Data Set

All tested methods inferred a different species tree. We first counted the number of splits that differ between the inferred trees and the multifurcating NCBI taxonomy (Federhen 2012) tree. The SpeciesRax, ASTRAL-Pro, and FastMulRFS tools disagree on five splits, MiniNJ on six splits, and DupTree disagrees on 20 splits.

Then, we focused on the five splits on which SpeciesRax disagrees with the NCBI taxonomy tree that we downloaded from the Ensembl Compara database. Among those discordant splits, the SpeciesRax tree seems to clearly violate only one well established phylogenetic relationship (Venkatesh et al. 2014): The elephant shark, which is a Chondrichtyian, is placed by SpeciesRax within Osteicthyians, as sister to Sarcopterygii. Note that all tested methods (ASTRAL-Pro, FastMulRFS, DupTree, and MiniNJ) agree with SpeciesRax.

In the following, we analyze the remaining four disagreements.

First, SpeciesRax (as well as all other competing tools) places Cichliformes as sister to Ambassidae whereas the taxonomy places Pomacentridae as sister to Ambassidae. Most studies we have found support the taxonomy (Betancur-R et al. 2013; Near et al. 2013; Hughes et al. 2018) but other studies are undecided about the resolution of these clades and present trees inferred using different inference methods that support the three alternative resolutions (Eytan et al. 2015).

Another discordance with the taxonomy occurs within the avian subtree, between the Estrildidae, Fringillidae, and Passerellidae clades: the taxonomy groups the Estrildidae and Fringillidae together, whereas SpeciesRax, ASTRAL-Pro, and FastMulRFS group Fringillidae and Passerellidae together. A recently published 363 taxon bird phylogeny (Feng et al. 2020) agrees with SpeciesRax on this split and perfectly matches the remaining 24 taxon avian subtree we inferred.

In addition, all tested tools place Bos mutus (yak) and Bison bison closer to each other than to Bos taurus, whereas the taxonomy places B.mutus next to B.taurus. To our knowledge, the literature agrees with our resolution (Decker et al. 2009; Kumar et al. 2018).

The last inconsistency between the taxonomy and the SpeciesRax tree occurs among the Platyrrhini (monkey suborder) when placing Aotidae, Cebus/Saimiri, and Callitrichidae. This split is perhaps more interesting because SpeciesRax disagrees with the competing methods: the taxonomy places Cebus/Saimiri and Callitrichidae together, SpeciesRax places Aotidate and Callitrichidae together. The ASTRAL-Pro, FastMulRFS, MiniNJ, and DupTree tools all group Aotidate with Cebus/Saimiri. There exist studies that agree with the SpeciesRax (Perelman et al. 2011; Springer et al. 2012) but also the ASTRAL-Pro (Fabre et al. 2009) resolutions of these clades.

Plants23 Data Set

Both SpeciesRax and ASTRAL-Pro species trees disagree with the literature by placing the Malvales as sister to Malpighiales (instead of sister to Brassicales [Albert et al. 2013; Garcia-Mas et al. 2012]). The SpeciesRax species-driven quartet support scores positively support our resolution, suggesting a potentially misleading signal from the GFTs. When investigating the GFTs, we observed that the Brassicales genes often diverge much earlier than they should and that they are often placed outside of the Rosids clade to which they should belong. A hypothesis for this misleading signal is the apparent overestimation of the gene family sizes during the gene family clustering performed in the original study (Garcia-Mas et al. 2012) as many gene families contain 150 genes (the maximum family size cutoff used in the respective gene family clustering procedure). In addition, the GFTs exhibit clear clusters of genes covering all species separated by extremely long branches. We note, however, that DupTree and FastMulRFS correctly inferred the entire species tree.

Plants83 Data Set

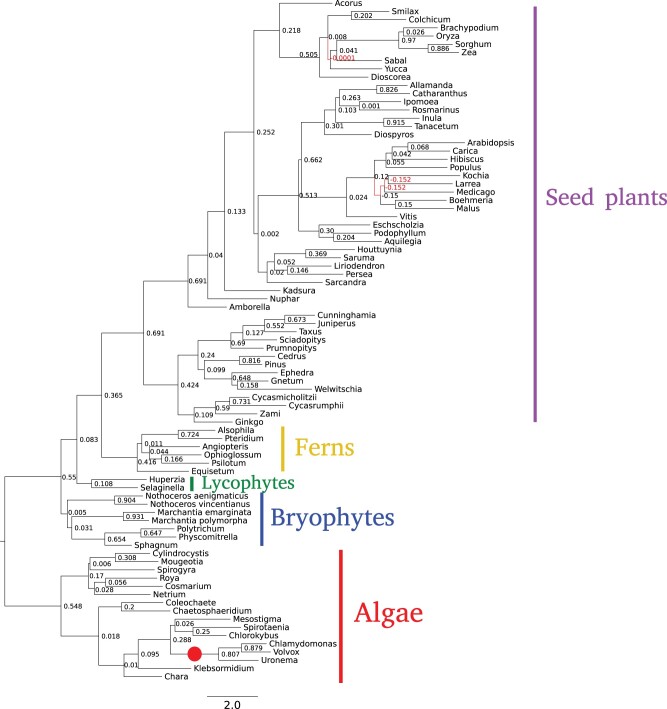
The unrooted topologies of the SpeciesRax (fig. 4), ASTRAL-Pro, and FastMulRFS trees are in very good agreement with current biological opinion on the Viridiplantae phylogeny, recovering Setaphyta, and the monophyly of bryophytes (Puttick et al. 2018; Leebens-Mack et al. 2019; Harris et al. 2020). The SpeciesRax tree further agrees with several recent analyses (Leebens-Mack et al. 2019; Harris et al. 2020) in placing the Coleochaetales algae as the closest relatives of Zygnematophyceae and Embryophyta (land plants). The tree inferred by DupTree features a number of disagreements with conventional views of plant relationships.

Fig. 4.

The species tree inferred with SpeciesRax from the Plants83 data set. The red circle indicates the expected root position. Support values displayed on the right side of each branch are EQPIC scores, reflecting the degree of agreement between the underlying GFTs and the corresponding branch. The values range between −1 and 1, with positive values indicating positive support for a branch from the GFTs. For instance, the branch that separates the seed plants from the other plants has a support of 0.691 (excellent support) and the branch that separates the bryophytes from the other plants has a support of 0.005 (low but positive support). Branches with a negative support are represented in red.

Fungi60 Data Set

All tools found a species tree that disagrees with the literature: They placed the clade formed by Chytridiomycota and Zygomycota between Basidiomycota and Ascomycota, which are typically grouped together (Lutzoni et al. 2004; Marcet-Houben and Gabaldón 2009). The positive extended quadripartition internode certainty (EQPIC) score computed with SpeciesRax along the relevant path shows that the quartets of the GFTs do support this incorrect split. We conclude that the GFTs contain a misleading signal around this split. One possible explanation is that Encephalitozoon cuniculi is evolutionary very distant from the remaining species, potentially causing a long branch attraction effect (Bergsten 2005). Apart from this split, SpeciesRax, ASTRAL-Pro, and FastMulRFS inferred the same tree, which agrees with the original species tree obtained via concatenation (Marcet-Houben and Gabaldón 2009). The tree inferred with DupTree differs from the SpeciesRax tree in one split.

Primates13, Cyanobacteria36, Vertebrates22, and Fungi16 Data Sets

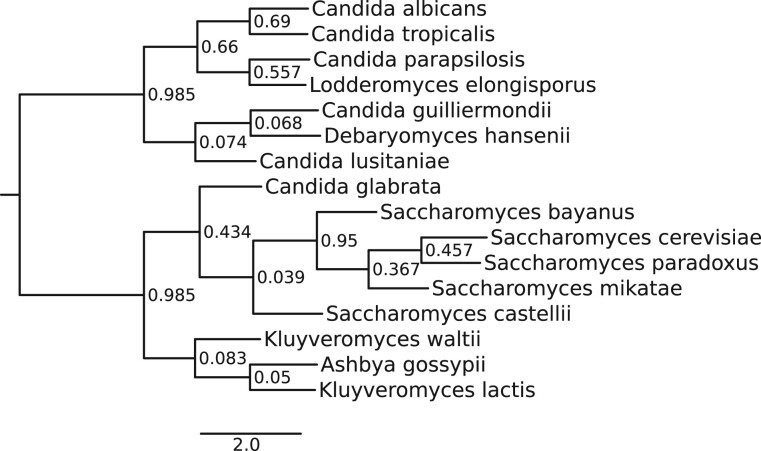
All tools inferred the same species trees for the Primates13, Cyanobacteria36, and Fungi16 (fig. 5) data sets and do not violate any well-established phylogenetic relationship. On the Vertebrates22 data set, all tested methods inferred trees that agree with the multifurcating NCBI taxonomy, but the inferred bifurcating trees are nonetheless different: ASTRAL-Pro, MiniNJ, and SpeciesRax inferred the same tree, which differs from the FastMulRFS tree by one split and the DupTree tree by two splits.

Fig. 5.

The species tree inferred with SpeciesRax from the Fungi16 data set.

Archaea364

The original authors (Dombrowski et al. 2020) suggested that one reason for the difficulty in resolving the archaeal tree was the presence of host–symbiont gene transfers in broadly conserved marker genes, in which members of the host-associated DPANN Archaea sometimes grouped with their hosts in single gene phylogenies. Using the full set of marker genes, the SpeciesRax tree recovered a clan (Wilkinson et al. 2007) of DPANN; that is, all DPANN Archaea clustered together on the tree. The unrooted SpeciesRax topology is congruent with several recent analyses of the archaeal tree (Raymann et al. 2015; Williams et al. 2017; Dombrowski et al. 2020).

Life92

SpeciesRax and ASTRAL-Pro both recovered the major lineages of Archaea and Eukaryotes, including the Euryarchaeota and “TACK” Archaea (Thaumarchaeota, Aigarchaeota, Crenarchaeota, and Korarchaeota) within the Archaea, and the SAR, Archaeplastida and Amorphea clades of Eukaryotes. ASTRAL-Pro resolves the Excavates into two separate clades (Discoba and Metamonada, with Trimastix branching between them), whereas SpeciesRax unites them as sister groups, albeit with very weak statistical support (–0.03); previous work is equivocal as to whether these two lineages form a monophyletic Excavata clade (Hampl et al. 2009; Burki et al. 2020).

SpeciesRax recovers the monophyly of Asgardarchaeota, whereas ASTRAL-Pro instead places one lineage, Odinarchaeota, with the TACK Archaea; the position recovered by SpeciesRax is the consensus view (Zaremba-Niedzwiedzka et al. 2017). However, SpeciesRax recovers Asgardarchaeota as sister to the TACK Archaea, albeit with low support (–0.0075). This topology is incompatible with a specific relationship between Eukaryotes and Asgardarchaeota, as supported by analyses of conserved marker genes (Spang et al. 2015; Zaremba-Niedzwiedzka et al. 2017; Williams et al. 2020). The unrooted tree inferred by ASTRAL-Pro groups Asgardarchaeota (without Odinarchaeota) with Eukaryotes, and is therefore compatible with an origin of the eukaryotic host cell from within the Asgardarchaeota.

Rooting Accuracy on the Simulated Data Sets

In this subsection, we compare the root placement accuracy of SpeciesRax and DupTree with respect to the root split score we introduced in the Experiments section. A lower root split score corresponds to a higher accuracy. On average, over all DLSIM experiments, SpeciesRax (rss = 0.43) recovers the true root placement more frequently than DupTree (rss = 0.59). As shown in figure 6a, SpeciesRax tends to infer more accurate root placements for increasing DL rates (rss = 0.63 in absence of DL events and rss = 0.23 under the highest DL rates). The results of the D TLSIM experiment suggest that SpeciesRax (rss = 0.50) is slightly negatively affected by HGT, whereas DupTree (rss = 0.92) almost always fails to recover the correct root placement. Figure 6b shows that SpeciesRax infers slightly less accurate root placements when the HGT rates increase (rss = 0.43 without HGT and rss = 0.53 with the highest HGT rate). We provide all root split score plots in Supplementary Material online.

Fig. 6.

Average root split score for increasing DL rates (no HGT) and for increasing HGT rates (fixed DL rates). (a) DL rates (DLSIM experiment) and (b) T rate, fixed DL rates (D TLSIM experiment)

Rooting Accuracy on the Empirical Data Sets

In the following, we conduct an in-depth assessment of the accuracy of the species tree root inference with SpeciesRax on the tested empirical data sets.

We first discuss the data sets on which SpeciesRax inferred a species tree root that agrees with the current literature. On the primates13 data set, SpeciesRax correctly places the species tree root between the Strepsirrhini and Haplorhini clades (Chatterjee et al. 2009). On the Fungi16 data set, the root inferred with SpeciesRax correctly separates the Candida and Saccharomyces clades (Butler et al. 2009). The root we inferred on the Vertebrates22 species tree correctly separates the Actinopterygii and Sarcopterygii clades (Meyer and Zardoya 2003). On the Plants23 data set, our species tree root correctly separates the Chlorophyta and Streptophyta clades (Leliaert et al. 2012). On the Fungi60 data set, we correctly find that E.cuniculi (Microsporidia clade) diverged earlier than the other clades contained in the data set (Nagy and Szöllősi 2017). On the Vertebrates188 data set, SpeciesRax infers a root that groups lampreys and hagfishes, on one side, and cartilaginous fishes, bony fishes, and tetrapods on the other side. The position of the vertebrate root is still controversial (Takezaki et al. 2003; Miyashita et al. 2019) and our resolution complies with some of the plausible scenarios discussed in the literature (Meyer and Zardoya 2003; Takezaki et al. 2003; Miyashita et al. 2019).

On the Plants83 data set, SpeciesRax agrees with the literature in placing Embryophyta (land plants) within the Streptophyte algae. However, the inferred root is three branches away from the consensus position, in the common ancestor of the Chlorophyta (Volvox, Chlamydomonas, and Uronema).

On the Cyanobacteria36 data set, the root placement inferred by SpeciesRax is one branch away from one of the three plausible roots inferred in a recent study (Szöllősi et al. 2012).

The Archaea364 data set only contained single-copy gene families, and thus no gene duplications. As a result, the position of the root was uncertain. However, the 95% confidence set of possible root placements obtained via the approximately unbiased (AU) test (Shimodaira 2002) was compatible with several recent suggestions in the literature, including a root between DPANN and all other Archaea (Williams et al. 2017; Dombrowski et al. 2020) and a root within the Euryarchaeota (Raymann et al. 2015), among a range of other positions within and between the major archaeal lineages.

The root inferred by SpeciesRax on the Life92 data set is biologically implausible as it is located between Viridiplantae and all other taxa. One possibility is that root inference for these data is affected by large differences in gene content among the included taxa. For example, the Viridiplantae (and other Archaeplastida) have chloroplasts, and so possess an additional source of bacterial-origin genes compared with other Eukaryotes and Archaea. To evaluate the impact of major gene content differences, we performed another SpeciesRax analysis in which the gene families covering less than half of the species were removed. In this second analysis, the root was inferred to lie between the Eukaryotes and Archaea. This root position is compatible with a three-domain tree of life hypothesis. However, this should be interpreted with caution, because the branch separating Eukaryotes and Archaea is one along which major gene content changes occurred, including (but not limited to) the acquisition of a bacterial genome’s worth of genes in the form of the mitochondrial endosymbiont (Roger et al. 2017).

Runtime

Before comparing runtimes, we emphasize again that we executed the experiments on a 40-core machine and that only SpeciesRax and ASTRAL-Pro provide a parallel implementation. Although this choice might appear to favor SpeciesRax and ASTRAL-Pro, we argue that the absence of parallelization constitutes a substantial limitation of the remaining tools as completing an analysis in less than 1 day on a parallel system instead of having to wait for several weeks represents a strong advantage.

We also emphasize that SpeciesRax is the only tested tool that can be executed across several compute nodes with distributed memory in contrast to ASTRAL-Pro that can only run on a single shared memory node. All tools, with the exception of MiniNJ, required huge amounts of memory for the largest data set (>200 GB on vertebrates188) and can therefore not be executed on most common servers. The SpeciesRax MPI implementation allows to distribute the memory footprint over different compute nodes, which is not feasible with the other tools.

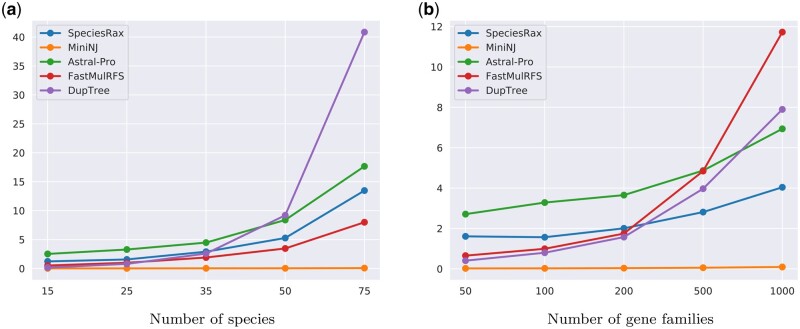
We show the runtimes for an increasing number of species and an increasing number of families for the simulated data sets in figure 7. Our MiniNJ method requires <0.1 s for all parameter combinations and is the fastest method we tested. The runtimes of DupTree and FastMulRFS grow faster with increasing number of gene families, and DupTree runtime quickly raises with the number of species. The SpeciesRax and ASTRAL-Pro runtimes are less affected by these parameters.

Fig. 7.

Average runtime in seconds for species tree inference. (a) Number of species and (b) number of families.

On almost all empirical data sets, MiniNJ and SpeciesRax are the fastest methods. On the two largest data sets (Plants83 and Vertebrates188), MiniNJ is at least one order of magnitude faster than SpeciesRax and SpeciesRax is at least one order of magnitude faster than all other methods. In particular, SpeciesRax only requires 1 h on 40 cores to infer the 188 vertebrate species tree with 188 species and 31,612 gene families.

Discussion

A Fast and Accurate Approach

We introduced two new methods for species tree inference from GFTs in the presence of paralogy. Our MiniNJ tool is a distance-based method that is faster than all tested methods while being at least as accurate as all other nonparametric methods for the majority of our simulated data experiments. In particular, MiniNJ inferred a species tree with 188 species in <1 min from more than 30,000 gene families. SpeciesRax, is a novel maximum likelihood tree search method that explicitly accounts for gene duplication, gene loss, and HGT events. Our SpeciesRax tool infers rooted species trees with branch lengths in units of mean expected substitutions per site. Further, to assess the confidence of the inferred species tree, we introduce several quartet-based support measures.

In terms of accuracy, SpeciesRax is more accurate than its competitors on simulated data sets, and up to twice as accurate under high duplication, loss, and HGT rates. On empirical data sets, SpeciesRax is on par with or more accurate than its competitors. In addition, among the tested tools, SpeciesRax, PHYLDOG, and DupTree are the only methods that can infer rooted species trees. On simulated data sets, SpeciesRax outperforms both PHYLDOG and DupTree in terms of root placement accuracy. SpeciesRax inferred the correct (biologically well-established) roots on six out of ten empirical species trees, and found roots that are close to the plausible roots in three out of the remaining four data sets (Plants83, Archaea364, and Cyanobacteria). For the most challenging-to-root data set (Life92), we managed to infer a plausible root by removing those gene families that only covered less than half of the species.

Despite being a compute-intensive maximum likelihood based tree search method, SpeciesRax is faster than all tested methods (except MiniNJ) on large empirical data sets. This is due to our fast method MiniNJ for inferring a reasonable starting tree and to our efficient reconciliation-aware search strategy. In addition, SpeciesRax provides a parallel implementation and can be run on distributed memory cluster systems. Thereby it facilitates conducting large-scale analyses (table 2).

Table 2.

Species Tree Inference Runtimes for All Tested Tools.

Data Set	FastMulRFS	DupTree	ASTRAL-Pro	SpeciesRax	MiniNJ
Primates13	62 s	18 s	38 s	14 s	2 s
Cyanobacteria36	19 s	26 s	12 s	14 s	<1 s
Fungi16	9 s	7 s	18 s	7 s	<1 s
Vertebrates22	9 min	5 min	2 min 45 s	2 min 30 s	7 s
Fungi60	16 min	17 min	1 min 30 s	1 min	2 s
Plant23	9 min	6 min	1 min 35 s	2 min	8 s
Life92	6 h	2 h 20 min	31 min	6 min	2 s
Archaea364	11 min	6 h	1 min	14 min	10 s
Plants83	4 h	2 h 40 min	1 h 40 min	8 min	27 s
Vertebrates188	14 days	3.5 days	12 h	1 h 5 min	53 s

Further, SpeciesRax has been integrated into our GeneRax tool that is available via Github and BioConda (Grüning et al. 2018). With GeneRax, users can execute the following (optional) steps in one single run: GFT inference from the gene alignments, rooted species tree inference with SpeciesRax from the GFTs, species-tree aware GFT correction, and GFT reconciliation with the rooted species tree. Alternatively, SpeciesRax can be used to infer the root of a user-specified species tree (typically obtained from concatenation methods) before inferring reconciliations. Thus, GeneRax has become a versatile, one-stop shop for executing likelihood-based analyses on multiple-copy gene families.

Future Work

Despite our encouraging results, SpeciesRax still faces some challenges.

First, SpeciesRax cannot currently take into account GFT reconstruction error/uncertainty. This issue will become more prevalent with increasing taxon numbers and the associated increase in reconstruction uncertainty. Therefore, we intend to explore several ideas to overcome this limitation. A first idea consists in contracting the low-support branches of the GFTs and adapting our reconciliation model to multifurcating GFTs. Alternatively, we will explore if coestimating the species tree and the GFTs is feasible, as conducted by Phyldog (Boussau et al. 2012), for instance. Finally, we could take as input a distribution of GFTs for each gene family (instead of just one maximum likelihood GFTs) and integrate over this distribution of per gene family GFTs to compute the likelihood score. Such a GFTs distribution could obtained from Bayesian inference tools (Ronquist et al. 2012), from bootstrap trees (Felsenstein 1985), or from a set of plausible GFTs (Morel et al. 2021).

Secondly, we plan to implement more complex models of GFT evolution in SpeciesRax. First, the UndatedDTL model could be improved by modeling variation in DTL intensities among different branches of the species tree. This could, for instance, result in a better placement for microsporidia in the fungi60 tree, because this species is known to have a higher rate of losses than the other fungi. Furthermore, the UndatedDTL model implemented in SpeciesRax allows for HGTs between any pair of species, even if such HGTs are impossible timewise. Some models (Szöllősi et al. 2012) extract time information from the species tree to prohibit noncontemporary HGTs, that is, HGTs between species that have not coexisted and thus could not have exchanged genes. Finally, some promising work (Chan et al. 2017; Rasmussen and Kellis 2012; Li et al. 2020) has been conducted to account for both DTL events and ILS in a single model. We hope that models that better reflect the complexity of gene family evolution will yield more reliable species tree inference.

Finally, there now exists a range of quite distinct methods for species tree inference, and choosing the best method for analyzing a given data set is difficult. The available methods differ in the extent to which they consider ILS, HGT, phylogenetic uncertainty, and the underlying complexities of molecular sequence evolution. Some methods are also more scaleable than others. Because no method provides a full treatment of all of the complexities of genome evolution, prior biological opinion about the extent to which ILS, HGT, GFT error, or other signals might contribute in specific cases may help to guide the decision about which method to use. In addition to being able to infer species trees from multiple-copy gene families, one potential advantage of SpeciesRax is that it might be less sensitive to errors in orthology assignment, or—as observed in the archaeal data set—gene transfers of marker genes, because the DTL model can account for duplication-loss or transfer events. Benchmarking of the available tools on both empirical and simulated data sets will provide further insight into their relative performance and will help to develop practical guidelines for users interested in species relationships and genome evolution across the tree of life.

Materials and Methods

We recently (Morel et al. 2020) introduced the undatedDTL model, which is a phenomenological discrete time model that describes the evolution of a GFT along a species tree through gene duplication, gene loss, speciation, and HGT events. In addition, we described an algorithm for computing the corresponding reconciliation likelihood, that is, the probability of observing a set of GFTs $\mathcal{G}=(G_1,\dots ,G_n)$ given a rooted species tree S and the set Θ of duplication, loss, and HGT intensities describing the expected frequency of those events relative to the frequency of the speciation events:

$$L\left(S,\Theta |\mathcal{G}\right)={\prod }_{k=1}^{n}P\left(G_k|S,\Theta \right).$$ (1)

As already mentioned, SpeciesRax takes a set of unrooted GFTs as input. It starts its computations from an initial species tree that can either be randomly generated, user-specified, or inferred using our new distance method MiniNJ. Then, it performs a tree search for the rooted species tree S and the model parameters N that maximize the reconciliation likelihood $L(S,\Theta |\mathcal{G})$. At the end of the search, it also calculates support values for the inner branches of the inferred species tree from the GFTs. Finally, we also describe the adaptation of our likelihood score to better account for missing data and inaccurate assignment of sequences to gene family clusters.

Computing a Reasonable Initial Species Tree with MiniNJ

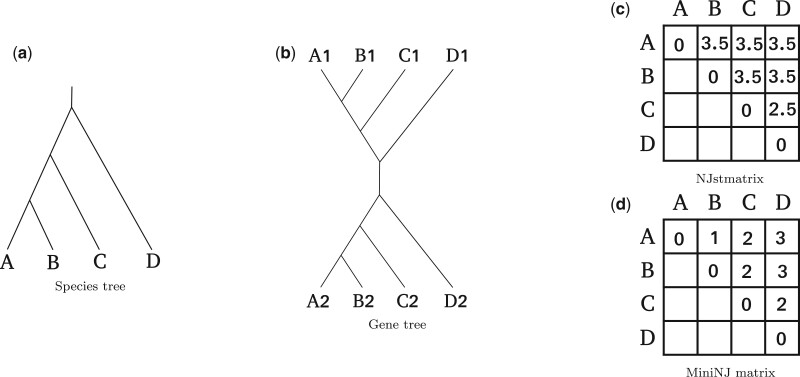
Here, we introduce MiniNJ (Minimum internode distance neighbor joining [NJ]), our novel distance-based method for inferring an unrooted species tree in the presence of paralogy. MiniNJ is fast, that is, it is well-suited for generating an initial species tree for the subsequent maximum likelihood optimization. MiniNJ is inspired by NJst (Liu and Yu 2011), a distance-based method that performs well in the absence of paralogy. Initially, we briefly outline the NJst algorithm, and subsequently describe our modifications.

NJst initially computes a distance matrix from the unrooted GFTs and then applies NJ to reconstruct the species tree. NJst defines the gene internode distance D_g such that $D_{\mathrm{g}}(x,y)$ is the number of internal nodes between the terminal nodes x and y in a GFT. NJst computes the distance between two species as the average over the internode distances between all pairs of gene copies mapped to those two species.

More formally, let a and b be two species. Let K be the number of GFTs. Let $M_k(a)$ be the number of terminal nodes from the GFT k mapped to species a. Let $x_{ik}(a)$ be the ith terminal node from the GFT k mapped to species a. NJst computes each element of the distance matrix $D_{\mathrm{NJst}}$ by first summing over all gene distances from all gene families, and then by dividing by the number of pairwise gene distances involved in this sum:

$$D_{\mathrm{NJst}}\left(a,b\right)=\frac{{\sum }_{k=1}^K{\sum }_{i=1}^{M_k\left(a\right)}{\sum }_{j=1}^{M_k\left(b\right)}{D}_g\left(x_{ik}\left(a\right),x_{jk}\left(b\right)\right)}{{\sum }_{k=1}^K{M}_k\left(a\right)M_k\left(b\right)}.$$ (2)

NJst has two drawbacks. First, it accounts for all pairs of gene copies, including paralogous gene copies that do not contain information about speciation events (see fig. 8). Secondly, it assigns very high (quadratic) weights to gene families comprising a high number of gene copies: for instance, a gene family k₁ with five gene copies in both species a and b will contribute 25 times to the distance between a and b, whereas a single-copy family k₂ will only contribute once. For instance, $\sum _{i=1}^{M_k(a)}\sum _{j=1}^{M_k(b)}{D}_g(x_{ik}(a),x_{jk}(b))$ is the sum over 25 gene internode distances for family k₁ and of only one gene internode distance for family k₂. Since the normalization by the number of gene internode distances is conducted after summing over all these quantities (with the denominator in eq. 2), the contributions of families k₁ and k₂ are unbalanced.

Fig. 8.

An example where MiniNJ computes distances that better reflect the true species tree than NJst. (a) The true rooted species tree. (b) A GFT resulting from a duplication at the root of the species tree. (c) The distance matrix $D_{\mathrm{NJst}}$ computed with NJst, incorrectly suggesting that all species are equidistant, except for C and D. This is the result of distance overestimation due to paralogous genes: for instance, species A and B are neighbors in the species tree, but the genes A2 and B1 are very distant from each other in the gene tree, because they start diverging at an early duplication event (paralogous genes). (d) Distance matrix $D_{\mathrm{MiniNJ}}$ computed with MiniNJ. The gene internode distances correctly reflect the species distances, because MiniNJ successfully pruned pairs of paralogous genes, such as A2 and B1, and only takes into account orthologous genes, such as A1 and B1.

MiniNJ adapts equation (2) to address these two issues. It assumes that, on average, two orthologous genes from two given, distinct species are closer to each other than two paralogous genes from the same two species (see for instance fig. 8). Note that this assumption does not always hold, for instance in the presence of HGT. MiniNJ attempts to discard pairs of paralogous gene copies by only considering the two closest GFT terminal nodes mapped to a pair of species for each family, according to the internode distance. let δ_abk be equal to 1 if gene family k contains at least one gene copy mapped to a and one gene copy mapped to b, and 0 otherwise. We define $D_{\mathrm{MiniNJ}}$:

$$D_{\mathrm{MiniNJ}}\left(a,b\right)=\frac{{\sum }_{k=1}^K\stackrel{\underset{M_k\left(a\right)}{i=1}}{\min }\stackrel{\underset{M_k\left(b\right)}{j=1}}{\min }{D}_g\left(x_{ik\left(a\right)},x_{jk}\left(b\right)\right)}{{\sum }_{k=1}^K{\delta }_{\mathit{abk}}}.$$ (3)

Note that for any two species a and b, all gene families that cover a and b contribute equally to $D_{\mathrm{MiniNJ}}(a,b)$.

MiniNJ then infers an unrooted species tree from this distance matrix using the NJ algorithm (Saitou and Nei 1987). The distance matrix computation has time complexity $O(\sum _{k=1}^K|g_k{|}^2)$ where $|g_k|$ is the number of gene sequences in the family k. The NJ algorithm has time complexity $O(|S{|}^3)$ where $|S|$ is the number of species. The overall time complexity of MiniNJ is thus $O(|S{|}^3+\sum _{k=1}^K|g_k{|}^2)$.

Maximum Likelihood Rooted Species Tree Search

Given a set $\mathcal{G}$ of unrooted GFTs, SpeciesRax implements a hill-climbing algorithm to search for the rooted species tree S and optimize the set of model parameters Θ (duplication, loss, and HGT intensities) that maximize the reconciliation likelihood $L(S,\Theta |\mathcal{G})$. In this section, we only briefly explain our search algorithm. We provide a more detailed description of the different steps and of the order by which we apply them in Supplementary Material online.

The search starts from an initial species tree S and a default or user-specified set of initial model parameters ${\Theta }_0$. Then, we alternate between optimizing the species tree root position, Θ, and the species tree topology until we cannot find a configuration with a better likelihood. We optimize the root position by evaluating the likelihood of the neighbors of the current candidate root position and repeat this process until we do not encounter a neighboring candidate root position with a higher likelihood. We optimize Θ via a gradient descent approach. To optimize S, we alternate between two complementary tree search strategies that both rely on subtree prune and regraft (SPR) moves: The transfer-guided SPR search assumes that the SPR moves that reduce the number of required HGT events necessary to reconcile the GFT with the species tree are more likely to improve the reconciliation likelihood. In Supplementary Material online, we detail how we identify and apply such SPR moves. The local SPR search tries all possible SPR moves within a user-specified radius (one by default). In both search strategies, when SpeciesRax finds a species tree $S\prime$ with a better likelihood than S, it replaces S by $S\prime$.

When applying the final root position search, SpeciesRax outputs the per-GFT likelihood scores for all tested root positions. The file with these per-GFT likelihoods can then be further analyzed with the Consel tool (Shimodaira and Hasegawa 2001) to perform a range of statistical significance tests (e.g., the AU test [Shimodaira 2002]) to generate a confident set of root placements.

Calculating the reconciliation likelihood under the UndatedDTL model represents the major computational bottleneck. To reduce its computational cost, we introduce several approximations. The first approximation is to ignore certain combinations of events that are unlikely to happen (e.g., a gene being transferred twice in a row), and which therefore exhibit a negligible contribution to the overall likelihood score. The second approximation is to dynamically estimate the most likely root position for each GFT during the species tree search, thereby avoiding the need to evaluate all possible GFT root positions. These approximations are described in more detail in Supplementary Material online.

Support Value Assessment

Here, we describe how SpeciesRax calculates branch support values on the species tree from a set of unrooted GFTs $\mathcal{G}$. We first revisit the definition of a speciation-driven quartet (SQ). Then, we explain how we use the SQ frequency to assess branch support values. Finally, we describe two alternative SQ-based scores, namely the quadripartition internode certainty (QPIC) and the EQPIC scores.

We first briefly revisit the definition of an SQ (Zhang et al. 2020). Let $\widehat{\mathcal{G}}$ be a set of rooted GFTs with internal nodes either tagged by “duplication” or “speciation” events as estimated from $\mathcal{G}$. A quartet from $\widehat{G}\in \widehat{\mathcal{G}}$ only contains information about the speciation events, if it includes four distinct species and if the lowest common ancestor of any three out of the four taxa of this quartet is a speciation node. Such a quartet is called SQ. We refer to Zhang et al. (2020) for a more formal definition of the SQ count and for its computation from a set of unrooted and unlabeled GFTs.

We now introduce several notations in order to define the SQ frequency of a pair of internal nodes in the species tree. Let S be an unrooted species tree. Let (u, v) be a pair of distinct internal nodes in S. The nodes u and v define a metaquartet$M_{u,v}=(A,B,C,D)$, where A and B (respectively, C and D) are the leaf sets under the left and right children of u (respectively, v) with S rooted at v (respectively, u). Let $z=(z_1,z_2,z_3)$ such that z₁ (respectively, z₂ and z₃) is the SQ count in $\mathcal{G}$ corresponding to the metaquartet topology $AB|CD$ (respectively, $AC|BD$ and $AD|BC$). Note that z₁ corresponds to the metaquartet topology that agrees with S ($(A,B|C,D)$) and that z₂ and z₃ correspond to the two possible alternative distinct metaquartet topologies ($AC|BD$ and $AD|BC$). Let $\widehat{z}=({\widehat{z}}_1,{\widehat{z}}_2,{\widehat{z}}_3)$ such that ${\widehat{z}}_i=\frac{z_i}{z_1+z_2+z_3}$ for $i\in (1,2,3)$. We define the SQ frequency of (u, v) in S given $\mathcal{G}$ as $SQ{F}_{\mathcal{G}}(u,v)={\widehat{z}}_1$.

The SQ frequency represents how many SQs around u and v support the species tree topology. However, it does not always reflect if $(AB|CD)$ is the best supported of the three possible metaquartet topologies, in particular when $(1/3)<z_1<(1/2)$. For instance, $\widehat{z}=(0.4,0.3,0.3)$ suggests that $(AB|CD)$ is the correct topology, but $\widehat{z}=(0.4,0.6,0.0)$ suggests that the alternative topology $(AC|BD)$ is better supported. Thus, the value of z₁ alone is not sufficiently informative to assess our confidence in a branch defined by u and v.

To overcome this limitation, we therefore also compute the QPIC and EQPIC scores introduced in Zhou et al. (2020). Note that these scores were initially defined for single-copy gene families. Because SpeciesRax operates on multiple-copy families, we adapt the scores by only counting SQs instead of counting all quartets. Let (u, v) be two distinct nodes of S.

$$\mathrm{qpic}\prime (u,v)=1+{\widehat{z}}_1\mathrm{l}\mathrm{og}\left({\widehat{z}}_1\right)+{\widehat{z}}_2\mathrm{l}\mathrm{og}\left({\widehat{z}}_2\right)+{\widehat{z}}_3\mathrm{l}\mathrm{og}\left({\widehat{z}}_3\right)$$ (4)

$$\mathrm{QPIC}(u,v)=\left\{\begin{array}{cc}0& \text{if} z_1=z_2=z_3=0\\ \mathrm{qpic}\prime (u,v)& \text{if} z_1=\max (z_1,z_2,z_3)\\ -\mathrm{qpic}\prime (u,v)& \text{otherwise}\end{array}\right..$$ (5)

In particular, if u and v are neighbors, we define the QPIC of the branch e between u and v as $\mathrm{QPIC}\left(e\right)=\mathrm{QPIC}(u,v)$. One limitation of the QPIC score is that it discards all SQs defined by nodes u and v that are not neighbors. Zhou et al. (2020) extends the QPIC score by defining the EQPIC score of a branch e:

$$\mathrm{EQPIC}\left(e\right)=\mathrm{mi}{\mathrm{n}}_{\{u,v\}\in \mathcal{N}\left(e\right)}\left(\mathrm{QPIC}\right(u,v\left)\right),$$

where N(e) is the set of node pairs {u, v} such that the branch e belongs to the unique path between u and v.

Note that both QPIC and EQPIC scores range between –1 and 1. They take positive values when they support the relevant metaquartet topologies of the species tree S and negative values otherwise.

We also note that support values are not calculated under the probabilistic UndatedDTL model that SpeciesRax employs to infer the species tree. Instead, they provide a measure of the topological conflict between the GFTs and each branch of the species tree based on a nonprobabilistic heuristic.

Accounting for Missing Data

We refer to missing data as gene copies that are absent from a gene family to which they should belong. This can occur, for instance, when some gene sequences have not been sampled or when the gene family clustering is inaccurate. Missing data is problematic for species tree estimation, in particular, when the missing data pattern distribution is nonrandom (Xi et al. 2016). In particular, reconciliation methods like SpeciesRax can be affected by missing gene copies: for instance, if sequences for a subset of the species under study have not been sampled for several families, the statistical reconciliation model will attempt to explain these missing gene copies via additional, yet incorrect loss events. Thus, a candidate species tree that groups such a subset of species into one subtree will typically exhibit a better reconciliation likelihood score than the “true” species tree. This is the case, because only one loss event per family would be necessary to explain all missing gene copies. We alleviate this problem to a certain extent by deploying a species tree pruning mode: let G be a GFT and S a species tree. We replace the reconciliation likelihood term L(S, G) by L(S′, G), where S′ is obtained from S by pruning all species that are not covered by G and by removing internal nodes of degree 1 until the tree is bifurcating. Thus, if a species is not present in a family, the reconciliation likelihood of this family does not depend on the position of this species in the species tree.

A downside of this approach is that it can disregard some true gene loss events. In addition, it is currently unclear how the pruned mode affects the properties of the reconciliation likelihood model. The experiments presented here suggest that the pruned mode neither decreases reconstruction accuracy nor increases runtimes. A mathematically more appealing solution would directly incorporate missing data in the UndatedDTL model.

Parallelization

We parallelized SpeciesRax with MPI (Message Passing Interface) which allows to execute it using several compute nodes with distributed memory (e.g., compute clusters). We distribute the gene families among the available cores to parallelize the reconciliation likelihood computation.

Experiments

Tested Tools

In the following, we describe the settings we used for executing all tools (summarized in table 3) in our experiments. We ran DupTree, FastMulRFS, and MiniNJ with default parameters. Among the four outputs that FastMulRFS provides, we discarded the outputs that may contain multifurcating trees (“majority” and “strict”). Among the two remaining outputs (“greedy” and “single”), we selected “single” because it performed slightly better in our experiments.

Table 3.

Software Used in Our Benchmark.

Method	Type	Infers Root	Ref.
NJst	Distance matrix	No	Liu and Yu (2011)
DupTree	Parsimony	Yes	Wehe et al. (2008)
FastMulRFS	Distance to GFTs	No	Molloy and Warnow (2020)
ASTRAL-Pro	Quartet	No	Zhang et al. (2020)
PHYLDOG	Maximum likelihood	Yes	Boussau et al. (2012)
MiniNJ	Distance matrix	No	This study
SpeciesRax	Maximum likelihood	Yes	This study

We used our own (re-)implementation of NJst (available in GeneRax) because the existing implementation written in R was too slow for completing our tests in a reasonable time.

We executed ASTRAL-Pro using all available memory (“-Xms700G -Xmx700G”) and a fixed random number seed (“– seed 692”).

We executed PHYLDOG using all available cores on the server (“mpiexec -np 40”) and conducted a nearest-neighbor interchange-based (NNI) tree search for the GFT optimization (“rearrangement.gene.tree=nni”). We used MiniNJ to generate the starting species tree.

We executed SpeciesRax starting from a MiniNJ tree, with the UndatedDTL model, with per-family duplication, HGT, and loss (DTL) rates. We also disabled all irrelevant steps such as gene tree optimization (“-s MiniNJ –optimize-species-tree –do-not-optimize-gene-trees –rec-model UndatedDTL –per-family-rates –skip-family-filtering –do-not-reconcile”). For the experiments on empirical data sets, we added the SpeciesRax option “–prune-species-tree” described in Account for Missing Data. To analyze the empirical data set that do not contain any multiple-copy gene families (Archaea364), we disabled the gene duplication events in the UndatedDTL model (option “–no-dup”).

Hardware Environment

We executed all experiments on the same machine with 40 physical cores, 80 virtual cores, and 750GB RAM. Note that DupTree, NJst, and MiniNJ only offer a sequential implementation. In contrast, SpeciesRax, FastMulRFS, ASTRAL-Pro, and PHYLDOG provide a parallel implementation (although FastMulRFS has at least one step that seems to be run sequentially) and were run using all available cores. We discuss the implications of this choice in Results.

Simulated Data Sets

We generated simulated data sets with SimPhy (Mallo et al. 2016) to assess the influence of the simulation parameters on the reconstruction accuracy of the methods.

The parameters we studied are the average number of sites per gene family MSA, the number of families, the size of the species tree, the average DTL rates, the GC rate, the GFT branch length scaler, and the population size. For each parameter we studied, we varied its value while keeping all other parameters fixed. In addition, we varied the DL rates while keeping the T rate fixed, and also varied the T rate while keeping the DL rates fixed. We generated 100 replicates for each set of parameter values. We executed the entire experiment twice, once including HGTs (D TLSIM experiment) and once excluding HGTs (DLSIM experiment).

We reused the default parameters of the S25 (25 species per species tree) experiment of (Zhang et al. 2020) with some modifications that we list in the following. By default, we do not simulate ILS, because SpeciesRax does not model ILS. Therefore, the species tree inference is easier than in the original S25 experiment. To make the reconstruction more challenging and to reduce the computational cost of the entire experiment, we reduced the number of families from 1,000 to 100. To increase the heterogeneity among gene families, we used a log-normal distribution for the sequence length (with, by default, 100 sites per sequence on average) and for the DTL rates. In the D TLSIM experiment, we simulated under the distance-independent HGT model (i.e., the receiving species is uniformly sampled from all contemporary species) and we set the default average HGT rate equal to the default average duplication rates. We provide a detailed list of the SimPhy parameters in Supplementary Material online.

We inferred the GFTs with ParGenes (Morel et al. 2018), performing one RAxML-NG search on a single random starting tree per gene family under the general time reversible model of nucleotide substitution with four discrete gamma rates (GTR + G4) (Tavaré 1986; Yang 1993). Then, we inferred the species trees from the inferred GFTs with every tool listed in table 3.

Finally, for each data set, we assessed the species tree reconstruction accuracy by computing the average relative RF distance between each inferred species tree and the corresponding true species tree using the ETE Toolkit (Huerta-Cepas et al. 2016). We assessed the root placement accuracy of SpeciesRax, DupTree, and PHYLDOG by introducing the root split score. It is defined as the proportion of inferred rooted species trees whose root incorrectly splits the species into two groups compared with the split induced by the correct, true root. The remaining methods we tested do not infer rooted species trees.

Due to excessive runtimes, we only executed PHYLDOG on the 100 replicates of the default parameter set of the DLSIM experiment. PHYLDOG was more than two orders of magnitude slower than all the other methods and less accurate than SpeciesRax (see Supplementary Material online).

Empirical Data Sets

We used empirical data sets from various sources to cover a wide range of organisms including plants, fungi, vertebrates, bacteria, and archaea. We describe these data sets in table 4. When the data sets included outgroups, we excluded them from the analysis, because SpeciesRax does not need any outgroup to root the species trees. For data sets where we pruned outgroups and for which alignments were available, we reinferred the GFTs from the alignments. This was done to avoid any potential bias in the tree reconstruction that could be caused by the outgroup (Holland et al. 2003). When the alignments were available, we used GeneRax to correct the GFTs and to estimate the DTL intensities on those empirical data sets, to confirm that they fall in the same range as the DTL intensities estimated from the simulated data sets (see Supplementary Material online). In the following we describe in detail how we assembled each empirical data set.

Table 4.

Description of the Empirical Data Sets Used in Our Benchmark.

Data Set	Families	Genes	GFTs	Gene Data Source
Primates13	16,670	268,338	Inferred	Ensembl Compara
Cyanobacteria36	1,099	41,035	Inferred	Hogenom
Vertebrates22	18,829	1,521,587	Extracted	PhylomeDB
Fungi16	7,180	85,866	Extracted	Butler et al. (2009)
Fungi60	5,665	391,471	Inferred	PhylomeDB
Plants23	21,469	1,652,464	Inferred	PhylomeDB
Life92	41,222	628,747	Inferred	Williams et al. (2020)
Archaea364	150	46,801	Inferred	Dombrowski et al. (2020)
Plants83	9,237	1,294,695	Extracted	1000k plants
Vertebrates188	31,612	3,725,332	Inferred	Ensembl Compara

Note.—Data set names are suffixed by the number of species in the respective data set. Families are the number of input gene families. Genes are the total number of gene copies in the data set. GFTs indicate if we inferred the GFTs (“inferred”) or if we extracted them from the data source (“extracted”). Gene data source is the database or the project/publication from which the GFTs and/or gene family alignments were obtained.

Primates13 and Vertebrates188 Data Sets

We extracted the alignments comprising 199 species from the Ensembl Compara database (Zerbino et al. 2018). We removed five nonvertebrate species to obtain the Vertebrates188 data set. Further, we extracted 13 primate species to obtain the Primates13 data set. For both data sets, we inferred the GFTs with ParGenes under the GTR + G4 model with one random starting tree per RAxML-NG maximum likelihood search.

Cyanobacteria36 Data Set

We reused the protein alignments of a previous study (Szöllősi et al. 2013) covering 36 cyanobacteria species to generate the Cyanobacteria36 data set. We inferred the GFTs with ParGenes under the same substitution model used in the original study (LG + G4 + I) with one random starting tree per RAxML-NG search.

Fungi16 and Plants83 Data Sets

The Fungi16 and Plants83 data sets, respectively, correspond to the Plant (1 kp) and Fungal data sets studied in Zhang et al. (2020). We downloaded the respective GFTs from https://github.com/chaoszhang/A-pro_data (last accessed January 18, 2022).

Fungi60, Plants23, and Vertebrates22 Data Sets

We extracted data sets from three different phylomes of the PhylomeDB (Huerta-Cepas et al. 2014) database: vertebrates (phylome ID = 200), fungi (phylome ID = 3), and plants (phylome ID = 84). We removed the two outgroup species (Arabidopsis thaliana and Human) from the fungi phylome to generate the Fungi60 data set. We removed the five outgroup species (outgroups: human, Drosophilia, Caenorhabditis elegans, Saccharomyces cerevisiae, and Plasmodium falciparum) from the plant phylome to generate the plants21 data set. We reinferred the GFTs of both, the fungi and plants data sets using ParGenes with best-fit model selection enabled (-m option) and one random starting tree per RAxML-NG search. We generated the Vertebrates22 data set from the vertebrates phylome. Here, we did not remove any outgroup and did therefore not reinfer the corresponding GFTs.

Life92 Data Set

To compare to the supertrees inferred in the original study (Williams et al. 2020), we extracted the original GFTs covering 92 species from the Eukaryote and Archaea domains. To take advantage of the signal from duplications and transfers, we also inferred new homologous gene families from the genomes used in that study. To do so, we performed all-versus-all Diamond (Buchfink et al. 2015) searches, then clustered gene families using mcl (Enright 2002) with an inflation parameter value of 1.4. As in the original study, sequences were aligned using MAFFT (Katoh and Standley 2013) and poorly aligning positions removed using BMGE 1.12 (Criscuolo and Gribaldo 2010) with the BLOSUM30 matrix.

Archaea364 Data Set

We downloaded the MSAs of the marker proteins from the original study (Dombrowski et al. 2020). We inferred the GFTs with ParGenes using the LG + G4 substitution model.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.