Noninvasive noncontact speckle contrast diffuse correlation tomography of cerebral blood flow in rats

Abstract

Continuous and longitudinal imaging of cerebral blood flow (CBF) variations provide vital information to investigate pathophysiology and interventions for a variety of neurological and cerebral diseases. An innovative noncontact speckle contrast diffuse correlation tomography (scDCT) system was downscaled and adapted for noninvasive imaging of CBF distributions in rat brain through intact scalp and skull. Algorithms for 2D mapping and 3D image reconstruction of CBF distributions were developed and optimized. The continuous imaging capability of the system was shown by imaging global CBF increases during CO₂ inhalations and regional CBF decreases across two hemispheres during sequential unilateral and bilateral common carotid artery ligations. The longitudinal imaging capability was demonstrated by imaging CBF variations over a long recovery period of 14 days after an acute stroke. Compared to the 2D mapping method, the 3D imaging method reduces partial volume effects, but needs more computation time for image reconstruction. Results from this study generally agree with those reported in the literature using similar protocols to induce CBF changes in rats. The scDCT enables a relatively large penetration depth (up to ~10mm), which is sufficient for transcranial brain measurements in small animals and human neonates. Ultimately, we expect to provide a noninvasive noncontact cerebral imager for basic neuroscience research in small animal models and clinical applications in human neonates.

1. Introduction

Cerebral blood flow (CBF) is tightly coupled with neural activities and instantly regulated to meet brain metabolic demands. Cerebral hyper-perfusion (excessive CBF) can raise intracranial pressure or induce headache or hemorrhage, while cerebral hypo-perfusion (insufficient CBF) can lead to depression of cortical function or ischemic injury. Therefore, continuous and longitudinal monitoring of CBF variations is crucial for understanding pathological mechanisms and developing medical interventions for a variety of neurological and cerebral diseases. Small rodents (mice and rats) have been the leading model organisms used in preclinical neuroscience research (Chesselet and Carmichael, 2012; Durukan et al., 2008; Ellenbroek and Youn, 2016; Schaller and Graf, 2002; Stagliano et al., 1999). Since their introduction to the laboratory more than one century ago, rodents still make up 95% of the animal models used in biomedical research today. Mice have a more prominent role compared to rats due to the availability of a much larger genetic toolbox, while rats are closer to humans (especially neonates) compared to mice.

Technologies capable of imaging CBF in both animals and humans are critically needed for translational studies of cerebral diseases, which are often associated with regional cerebral ischemia and hypoxia. In contrast to large imaging modalities such as computer tomography (CT), magnetic resonance imaging (MRI) and positron emission tomography (PET), optical instruments are fast, continuous, inexpensive, and portable (Boas et al., 2004; Cheng et al., 2012; Culver et al., 2003; Dragojević et al., 2017; Shang et al., 2011; Zhou et al., 2006). Near-infrared (NIR) based optical imaging techniques, such as traditional diffuse optical tomography (DOT) and more recently developed diffuse correlation tomography (DCT), have been used as noninvasive bedside means for continuous monitoring of cerebral blood oxygen saturation (StO₂) and CBF, respectively (Agochukwu et al., 2017; Buckley et al., 2014; Cheng et al., 2012; Durduran and Yodh, 2014; Huang et al., 2015c; Taber et al., 2010; Yu et al., 2003; Zhou et al., 2006). However, most DOT/DCT systems lack the combination of spatial resolution and wide field-of-view (FOV) to image spatially distributed brain functions. A few high-density DOT systems use numerous discrete sources and detectors coupled with fiber bundles to a head cap/helmet, facilitating improved spatial resolution over a large FOV and better separation of cerebral signals from overlaying scalp and skull (Eggebrecht et al., 2014; Ferradal et al., 2016; Hebden et al., 2002). However, expanding the FOV to cover a significant portion of the head introduces great challenges in high-channel-count instrumentation, fiber-optic-scalp coupling, and data quality management (Eggebrecht et al., 2014; Ferradal et al., 2016; Hebden et al., 2002; Huang et al., 2015b; Lin et al., 2014). Also, DCT devices employ a limited number of very expensive single-photon-counting avalanche photodiodes (APDs) for blood flow detection, leading to a high instrument cost and poor temporal-spatial resolution (Huang et al., 2015b; Lin et al., 2014).

Using charge-coupled devices (CCDs) with thousands of 2D array pixels, high-density sampling can be achieved quickly (Zhang, 2014). With unfocused wide-field illumination, CCDs have been used in microscopy to map 2D distributions of cerebral oxygenation (via optical intrinsic signal imaging: OIS technique) (Teichert and Bolz, 2017; Zhou et al., 2017) or CBF (via laser speckle contrast imaging: LSCI technique) (Durduran et al., 2004; Zhou et al., 2008) in cerebral cortices of rodents (mice or rats), where the scalp must be retracted to expose the skull and thicker skulls (rats) have to be thinned. In related mesoscopic imaging work, spatial frequency domain imaging (SFDI) and structured illumination DOT utilize structured wide-field illumination patterns and CCD detections to probe different depths of tissues up to a few millimeters (Cuccia et al., 2009; Gustafsson, 2005; Reisman et al., 2017). However, thus far, approaches with wide-field illumination and CCD detection have limited imaging penetration depths and thus are inadequate for noninvasive imaging of human brains including through the intact scalp and skull of neonates.

There have been recent advancements towards using focused point illumination and CCD detection of spatial diffuse speckle contrasts to facilitate rapid measurements of blood flow variations in relatively large and deep tissue volumes. These advanced techniques include diffuse speckle contrast analysis (DSCA), speckle contrast optical tomography (SCOT), and speckle contrast diffuse correlation tomography (scDCT). These technologies are inherently based on the same concept despite differences in nomenclature and technological evolution. DSCA uses optical fibers to deliver laser light and guide the detection by a camera sensor, thus enabling contact and spectroscopic (not tomographic) measurements of tissue blood flow with fiber-optic probes (Bi et al., 2013a, b; Bi et al., 2015; Seong et al., 2016). SCOT extends the concept with an analytical semi-infinite approximation for 3D image reconstruction of flow distributions in tissue-simulating phantoms and small mouse heads with retracted scalp (Dragojević et al., 2017; Varma et al., 2014). Our group has developed a noncontact reflectance-based scDCT technique (US Patent #9861319, 2016–2036) for 3D imaging of blood flow distributions in relatively large/deep tissue volumes with arbitrary boundaries (Huang et al., 2015a, 2017; Mazdeyasna et al., 2018). A finite-element-method (FEM)-based reconstruction has been developed to generate 3D flow images (Huang et al., 2015a, 2017; Lin et al., 2014). We have tested the scDCT system for 3D imaging of flow distributions in tissue-simulating phantoms, human forearms, human burned/wound tissues, and human mastectomy skin flaps (Huang et al., 2015a, 2017; Mazdeyasna et al., 2018). Results from these measurements indicate that the scDCT enables a fast and high-density 3D imaging of blood flow distributions with an adjustable depth ranging from 0 to 10mm over an adjustable region of interest (ROI).

The goal of the present study was to adapt this innovative scDCT system for noninvasive, continuous, and longitudinal imaging of CBF variations in rat brain through the intact scalp and skull. In contrast to large ROIs (up to 100 × 100 mm²) used in our previous studies for imaging large and deep human tissue volumes, a smaller ROI is required for imaging relatively smaller rat heads (~20 × 20 mm²). Thus, we modified the scDCT system and optimized the data processing algorithms for imaging CBF in rats. The performance of this optimized scDCT system was tested for continuous 3D imaging of CBF variations in rats during CO₂ inhalations (increasing CBF) and during unilateral and bilateral transient ligations of carotid arteries (reducing CBF). Furthermore, 2D maps of CBF generated from the same datasets were compared to 3D images to evaluate the impact of partial volume effects from the top layer of scalp and skull on deep brain signals. In addition, the longitudinal imaging capability was examined by intermittent monitoring of CBF variations in a rat over a 14-day recovery period after 1-h ischemia-reperfusion stroke. To the best of our knowledge, this paper reports the first noncontact 3D tomographic system that enables continuous and longitudinal 3D imaging of regional CBF distributions and variations in rat brain through intact scalp and skull.

2. Methods

2.1. Modified scDCT system

2.1.1. scDCT prototype and modification

Details for the scDCT prototype can be found in our previous publications (Huang et al., 2015a, 2017; Mazdeyasna et al., 2018; Yu et al., 2018). Fig. 1 shows the scDCT system for noncontact imaging of CBF in rats. Briefly, a galvo mirror (GVS002, Thorlabs) was used to deliver point NIR light generated from a long coherence laser (785 nm, CrystaLaser) to multiple positions (Fig. 1a and b). An Electron Multiplying CCD (EMCCD) (Pixels: 1002 × 1004; Cascade 1K, Photometrics) was used to detect spatial speckle contrasts in a selected ROI (Fig. 1c). A long-pass filter (>750 nm, EdmundOptics) was installed in front of the EMCCD to minimize the influence of ambient light. A pair of polarizers (LPNIRE050-B and LPNIRE200-B, Thorlabs) was added crossing the source and detection paths to reduce the source reflection directly from the tissue surface. A zoom lens (Zoom 7000, Navitar) was connected to the EMCCD camera for adjusting the size of the ROI. The fully noncontact probe was fixed on a 360° rotating holder for easy adjustment and alignment. All measurements in this study utilized an exposure time of 5 ms, and the F-number of the detection zoom lens was set as 11 to meet the Nyquist sampling rule (Boas and Dunn, 2010).

Fig. 1.

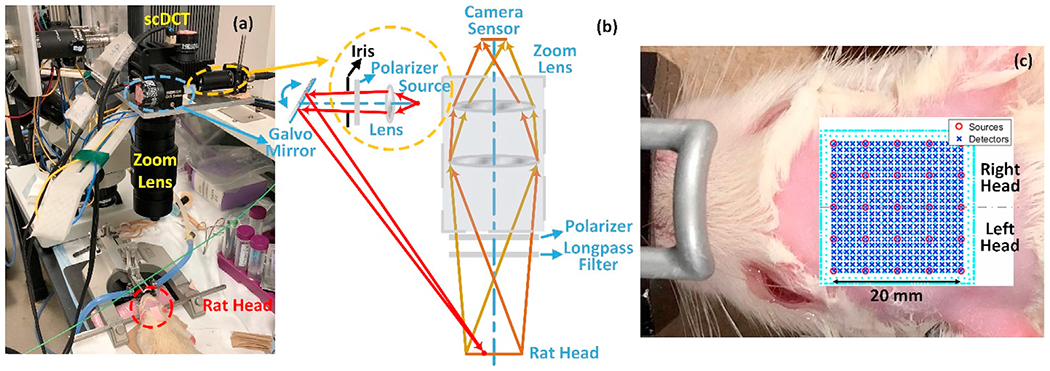
A modified scDCT system for imaging of CBF in rats. (a) Experimental setup for noncontact cerebral imaging of a rat. (b) Optical design of the modified scDCT. An iris was used to limit the size of light spot. (c) Rat head hair was shaved and removed with hair cream to expose a ROI of 20 × 20mm² on the rat head. 5 × 5 sources (circles) and 21 × 21 detectors (crosses) were evenly distributed within the ROI to acquire boundary flow data for 3D image reconstruction.

In this study, the scDCT prototype was downscaled for imaging the small rat head with a limited area of ~20 × 20 mm² (Fig. 1c). A major challenge in this downscaling was to achieve a sufficient spatial sampling density (i.e., with enough source-detector pairs) over a small ROI while maintaining good signal-to-noise ratios (SNRs). For this purpose, a lever-actuated iris (SM05D5, Thorlabs) was installed in the source path (Fig. 1b) and the iris was opened approximately one half of its full aperture (diameter = 3.5 mm) to confine the light spot diameter to be less than 0.5 mm. This modification allowed the scDCT to have a sufficient number of source positions (without any overlaps across sources) distributed over a small ROI. Furthermore, the exposure time of EMCCD camera (5 ms) was optimized based on our phantom test results (Supplementary Fig. 1) to obtain effective source-detector (S-D) separations ranging from 2 to 8 mm over the small ROI (Fig. 3 and Supplementary Fig. 2).

Fig. 3.

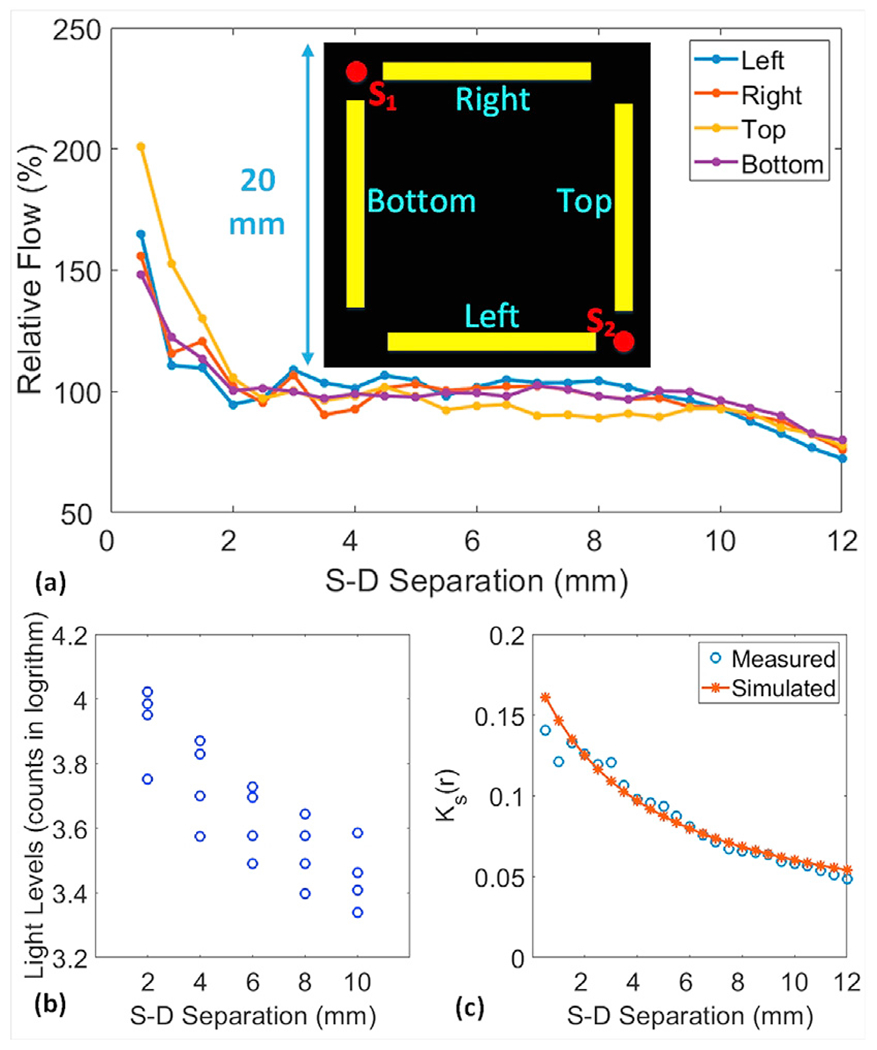
(a) Boundary flow distributions over the selected sources (S₁ and S₂) and detector arrays. Each detector array consisted of 24 detectors and S-D separations ranged from 0.5 to 12mm with an interval distance of 0.5 mm. Flow indices were normalized to their mean value to generate relative flow values for presentation. (b) Light intensities over the two sources (S₁ and S₂) and four detector arrays were logarithmically related to S-D separations. (c) Theoretical and measured K_s(r) distributions at different S-D separations across the source S₂ and left detector array.

2.1.2. Data acquisition and processing

Fig. 2 shows the flowchart for data acquisition and processing to obtain relative CBF (rCBF). To trade off temporal and spatial resolution, 25 source positions (5 × 5) were selected to cover a ROI of ~20 × 20 mm² on the rat head. The total sampling time for scanning over the 25 source positions was 20 s. The scDCT data were continuously collected via sequencing the source positions (adjusting the galvo mirror electronically), and two frames were taken at each source location for averaging to improve SNRs.

Fig. 2.

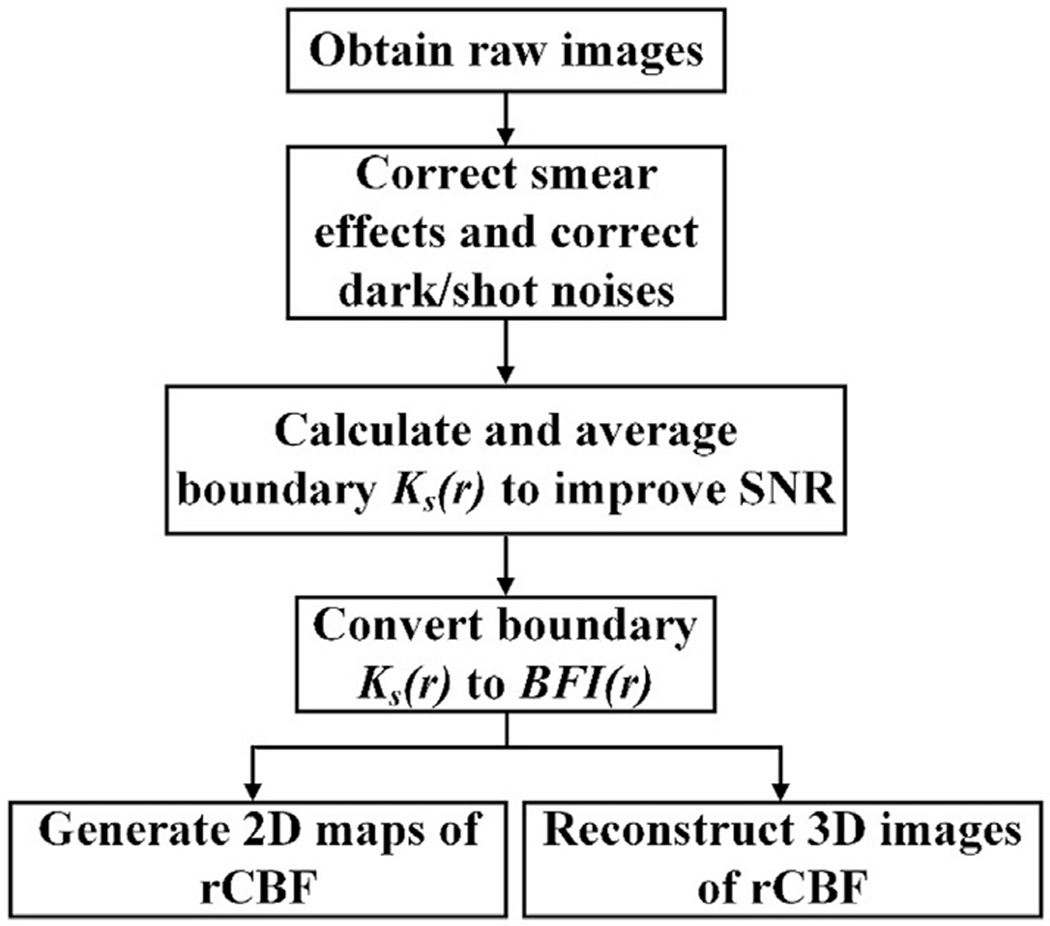
Data processing flowchart for generating 2D and 3D images of rCBF.

Raw images were first preprocessed to correct sources of EMCCD camera noise including the dark noise, shot noise, and smear effect (Huang et al., 2015a, 2017). The speckle contrast K_s(r) was quantified by calculating the ratio of spatial standard deviation (σ_s) and mean intensity I: K_s(r) = σ_s/I, in a pixel window of 7 × 7 pixels on the EMCCD camera. K_s(r) values were then averaged over 3 × 3 adjacent pixel windows in an area of 0.04 × 0.04 mm² (as a single detector) to improve detection SNRs. The scDCT collected speckle contrast data (K_s(r)) at all S-D pairs on the tissue surface (i.e., tissue boundary). The spatial resolution depends on the sampling density on tissue boundary, i.e., the number of S-D pairs per unit area. Averaging more pixel windows would result in one detector with a larger detection area (associated with a higher SNR) but a lower detection density (associated with a lower spatial resolution). A blood flow index (BFI(r)) on the tissue boundary was then extracted through the nonlinear relation between the boundary BFI(r) and K_s (r), measured by a defined detector. Derivation of this nonlinear relation can be found in our recent publication (Huang et al., 2017).

2.1.3. 2D mapping of CBF

The boundary BFIs were normalized to their baseline values to obtain rCBF. 2D images were generated by simply averaging boundary rCBF data obtained from the effective S-D separations of 2–8 mm, which were determined experimentally on standard homogenous tissue-simulating phantoms (see Section 2.2.1). To balance the spatial resolution and computation time for 2D mapping, 81 × 81 detectors (not shown in Fig. 1c) were selected over the ROI with the effective S-D separations ranging from 2 to 8 mm. The time to compute a 2D image was less than 10 s.

2.1.4. 3D image reconstruction of CBF

To balance the spatial resolution and computation time, 21 × 21 detectors (Fig. 1c) were defined in the selected ROI for 3D reconstruction. With this optimal configuration, the distance between two adjacent detectors was 1 mm. This allowed arrangement of 441 detectors without overlaps in the ROI on the rat head (see Fig. 1b). The boundary BFIs obtained from the effective S-D pairs (2–8 mm) were inserted into a modified NIRFAST program that was developed previously in our laboratory for expedient finite-element-method (FEM)-based scDCT tomographic reconstructions (Huang et al., 2015a, 2017; Lin et al., 2014).

The FEM based approach in NIRFAST recast the reconstruction into a nonlinear optimization problem (Dehghani et al., 2008). A median filter of level 2 was used to stabilize inherent experimental noise. The modified-Tikhonov regularization and biconjugate gradient stabilized iterative inversion scheme were implemented in NIRFAST for Jacobian construction. A regularization value λ of 10 was selected empirically. A projection error change of <2% was set as a stopping criterion for iterations; each image was reconstructed with 6–8 iterations of the Jacobian function.

The image reconstruction was processed in a 24 × 24 × 15 mm³ slab mesh with 1mm distance nodes (~8K nodes in total). The computation time for a single image reconstruction was ~15 min. The rCBF distribution was calculated by normalizing the reconstructed BFIs at the mesh nodes to their baseline values before the physiological manipulation.

2.2. Experimental protocols

2.2.1. Phantom experiments to determine the effective S-D pairs for CBF imaging

The use of tissue-simulating phantoms with known optical properties is a commonly accepted strategy for optical instrument calibration and validation (Huang et al., 2015a; Irwin et al., 2011). We have previously conducted experiments in heterogeneous tissue phantoms with the scDCT system to demonstrate 3D reconstruction capabilities/sensitivities of the technique for imaging targets with flow contrasts at a maximal depth of ~10mm (Huang et al., 2015a, 2017). In this study, homogenous Intralipid (Fresenius Kabi, Sweden) phantoms were used to calibrate effective S-D separations with the expectation that Intralipid particle flow was uniform everywhere inside the liquid solution. Brownian motion of the lipid emulsion (i.e., Intralipid particle flow) inside the liquid phantom mimics diffusive movements of red blood cells (i.e., blood flow) in a bulk tissue volume (Boas et al., 2016). In the phantom, the lipid concentration controls light scattering (${\mu }_s^{\prime }$) while the concentration of India ink (Black India, MA) controls light absorption (μ_a). Optical properties of the homogeneous phantom were initially set as μ_a = 0.025 cm⁻¹ and ${\mu }_s^{\prime }=8{\mathrm{cm}}^{-1}$ to match realistic tissues (Huang et al., 2015a, 2017). The homogeneous liquid phantom with a constant Intralipid particle flow was measured by the scDCT and boundary flow indices measured at different S-D pairs were evaluated to determine valid S-D separations for generating a stable/constant flow index.

2.2.2. Continuous imaging of rCBF variations in rats during CO₂ inhalations

All experimental procedures involving animals were approved by University of Kentucky Institutional Animal Care and Use Committee (IACUC). Nine adult male Sprague-Dawley rats (2–3 months) were imaged (Rat #1 to #9). The noncontact scDCT probe was set above the rat head for continuous imaging of rCBF distributions before, during, and after a 10% CO₂/90% O₂ stimulation for ~10 min (Kagstrom et al., 1983; Maggio et al., 2014; Ursino and Lodi, 1998; Wagerle and Mishra, 1988). CO₂ is a well-known vascular dilator, leading to CBF increase. Each rat was anesthetized with 1–2% isoflurane and placed on a heating blanket, and its head was fixed in a stereotaxic frame. Rat head hair was shaved with a clipper and cleaned with hair cream (Fig. 1c). After ~4-min baseline recording of scDCT data, the mixed gas of 10% CO₂ and 90% O₂ was administered through a rat nose cone using Matheson Mixer Rotameter for ~10min. CO₂ was then stopped, and scDCT measurements lasted for another ~10min to record CBF recovery. The rat was then returned to the cage for full recovery.

2.2.3. Continuous imaging of rCBF variations in rats during transient artery ligations

The nine rats used in the CO₂-inhalation experiment underwent transient bilateral ligations of common carotid artery (CCA) to create sequential decreases in CBF within the left and right cerebral hemispheres. One rat (Rat #9) was excluded from this protocol because of a surgical complication. The hair at cervical surgical site was shaved and removed with hair cream, and all other preparations were the same as described above. For CCA ligations, the cervical skin was disinfected with Betadine followed by 70% Ethanol. A midline incision was performed to expose and isolate both the left and right CCAs. A 6-0 braided nylon suture was placed around each CCA with a loose knot. After a baseline scDCT measurement for ~2 min, the left suture was tightened to ligate the left CCA for ~10 min. The right CCA was then also ligated to induce bilateral occlusion of the CCAs for another ~2 min. Finally, the ligation of right CCA was released and scDCT measurements continued for another ~2 min to record CBF recovery. During the scDCT measurement, surgical light was removed from the detection field to reduce light interference.

2.2.4. Longitudinal imaging of rCBF variations in a rat with stroke

To test the capability of scDCT for longitudinal monitoring of rCBF variations, one additional rat (Rat #10) undergoing a transient middle cerebral artery occlusion (MCAO) of the left hemisphere was imaged intermittently before, during and after stroke over a period of 14 days. The animal preparation for each scDCT measurement was the same as described above. For MCAO, the left CCA was exposed and isolated. A silicon-rubber coated 5-0 nylon filament was inserted through internal carotid artery (ICA) and advanced 15mm beyond the bifurcation of external carotid artery and ICA, to occlude the middle cerebral artery branching domain in the Circle of Willis or until a firm resistance was felt. Sixty minutes after left MCAO occlusion, the filament was withdrawn allowing for cerebrocortical reperfusion. The scDCT data was recorded immediately before and after inserting and withdrawing the filament at Day 0. For longitudinal monitoring, repeated scDCT measurements were performed at post-surgery days of 1, 3, 5, 9, and 14. Each measurement lasted for ~2 min and acquired CBF images were averaged for data analysis and reporting.

2.3. Statistical tests

Paired t-tests were used to evaluate differences in rCBF variations between different phases of stimuli (CO₂ inhalations and artery ligations) and spatial differences in rCBF variations between different layers of head tissues (i.e., scalp/skull versus cerebral cortex) or different hemispheres. p < 0.05 was considered statistically significant. In addition, the Hedges’ g for paired data was calculated as a measure of effect size (ES) to quantify the magnitude of difference between groups (Gibbons et al., 1993). The corresponding 95% confidence interval (CI) was also calculated. An ES > 0.8 was considered as a large magnitude of difference (Cohen, 1988).

3. Results

3.1. Effective S-D pairs determined by tissue-simulating phantom experiments

A homogenous phantom with constant Intralipid particle flow was used to evaluate and calibrate the modified scDCT instrument. Fig. 3a illustrates S-D arrangements including four detector arrays (yellow bars) near the selected two sources (S₁ and S₂) over a ROI of 20 mm × 20 mm. The right and bottom detector arrays were linked to S₁ and the left and top detector arrays were linked to S₂. Each detector array consisted of 24 detectors, which were 0.5–12 mm away from the source center with an interval of 0.5 mm. The relative flow values of Intralipid particles inside the liquid solution (Fig. 3a) were generated by normalizing flow indices at different S-D separations to their mean value as the reference. Thus, the observed stable/constant flow values at the effective S-D separations of 2–8 mm were with respect to other S-D separations. Means ± standard deviations of relative flow values were 104 ± 10%, 103 ± 15%, 95 ± 8%, and 99 ± 5% for left, right, top, and bottom detector arrays, respectively. Similar results were observed from other S-D links with the same range of S-D separations (i.e., from 2 to 8 mm) at different locations (data not shown). Fig. 3b illustrates the linear relation between the logarithmic scale of light intensities (counts) and S-D separations over the two sources (S₁ and S₂) and four detector arrays. Fig. 3c shows theoretical and measured K_s (r) distributions at different S-D separations across the source S₂ and left detector array. These results suggest that data obtained from the effective S-D separations of 2–8 mm matched expectations.

3.2. CBF responses in rats during CO₂ inhalations

Fig. 4a shows a white light image of the rat head (hair was removed) with a dotted line representing the middle line of rat head. Fig. 4b and c show typical 2D blood flow maps and corresponding time-course changes in rCBF before, during, and after CO₂ inhalation in one rat (Rat #5). Fig. 4d displays average time-course changes in rCBF over 9 rats. Table 1 summarizes rCBF changes and corresponding p and ES (with 95% CI) values at different phases of CO₂ stimulation, relative to their baseline values before CO₂ inhalation (assigned as ‘100%’). As expected, a significant increase in rCBF (mean ± standard error: 115 ± 7%, p < 10⁻³; ES = 2.19, 95% CI = 0.93 to 3.46) over all subjects was observed during CO₂ inhalation compared to its baseline value.

Fig. 4.

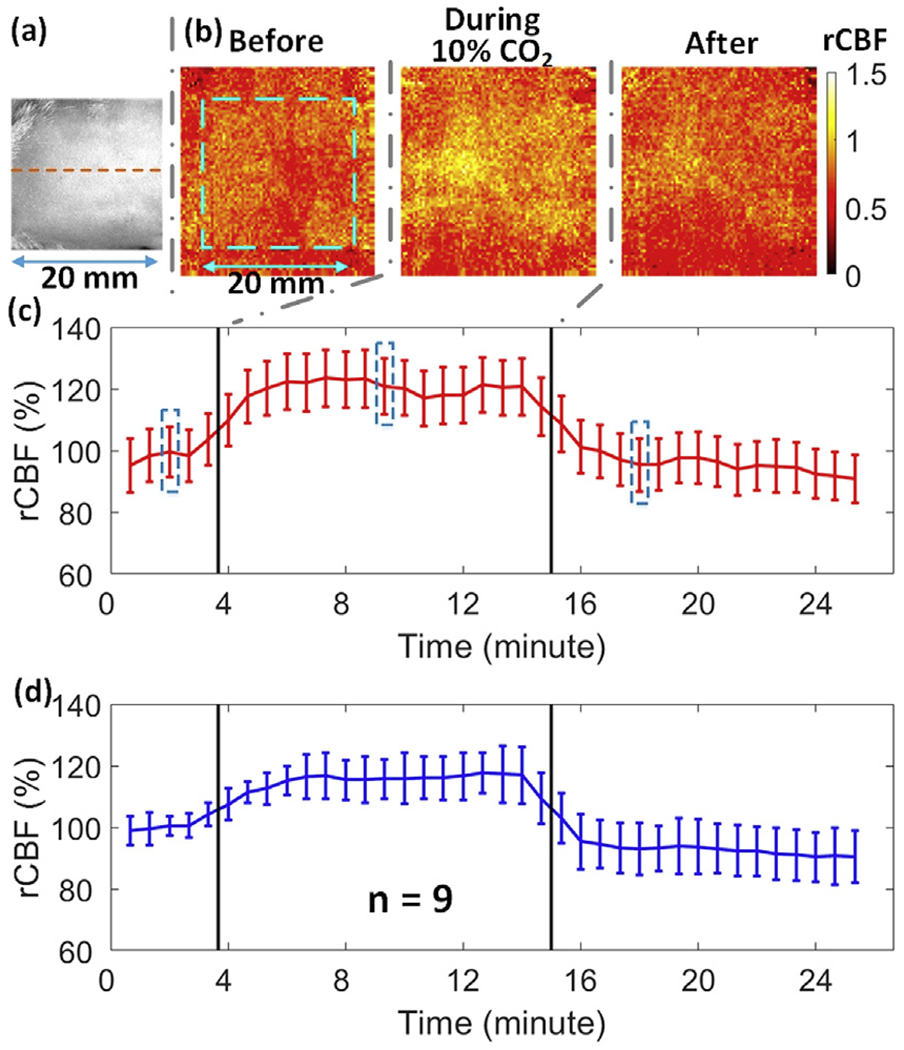
2D mapping of rCBF responses to CO₂ inhalation. (a) A white light photo of the rat head (hair was removed) with a dotted line representing the midline. (b) 2D rCBF maps before, during and after CO₂ inhalation in an illustrative rat (Rat #5). The dimension of the dashed box (20mm × 20 mm) is the same as (a). (c) Time-course rCBF variations in two hemispheres from Rat #5. Error bars represent standard deviations of regional rCBF. The blue dashed boxes represent the time of the images in Fig. 4b. Same in following figures. (d) Average time-course of rCBF variations over 9 rats. Error bars represent standard errors of regional rCBF over 9 rats.

Table 1.

rCBF changes induced by CO₂ inhalations compared to their baselines (100%) over 9 rats. Bolded differences are insignificant.

	9 Rats	CO2 Inhalation	Recovery
	2D Maps	115 ± 7% p < 10−3; ES = 2.19 (0.93, 3.46)	93 ± 8% p = 0.06; ES = 0.70 (−0.32, 1.73)
3D Images	0.5 mm Layer	118 ± 8% p < 10−3; ES = 2.16 (1.73, 4.68)	98 ± 8% p = 0.40; ES = 0.18 (−0.81, 1.18)
	3.0 mm Layer	119 ± 8% p < 10−3; ES = 2.30 (1.01, 3.60)	102 ± 5% p = 0.25; ES = 0.39 (−0.61, 1.40)
	Between Layers	p = 0.60; ES = 0.17 (−0.82, 1.17)	p = 0.02; ES = 0.93 (−0.11, 1.99)

Fig. 5a shows the cross-sectional views of 3D images at the depths of 0.5 mm and 3.0 mm, respectively, reconstructed from the same rat (Rat #5). Based on the photon diffusion theory, penetration depth of NIR light into biological tissues is approximately one half of the S-D separation distance (Irwin et al., 2011). Due to the limited size of the ROI on a small rat head, the effective S-D separations of the modified scDCT ranged from 2 to 8 mm. According to the anatomy of the rat head (0.5 mm scalp thickness and 1 mm skull thickness) (Nowak et al., 2011), a penetration depth of 3 mm should reach the surface of rat brain cortex while a depth of 0.5 mm should reach the rat scalp/skull. Fig. 5b and c show the time-course of rCBF during CO₂ inhalation in both layers of Rat #5 and over all 9 rats, respectively. The summary of rCBF changes in different layers is also included in Table 1. Significant increases in blood flow were observed at both depths of 0.5 mm (118 ± 8%; p < 10⁻³; ES = 2.16, 95% CI = 1.73 to 4.68) and 3.0 mm (119 ± 8%; p ≤ 10⁻³; ES = 2.30, 95%; CI = 1.01 to 3.60), while no significant differences were observed between the two layers (p = 0.60). There tended to be a difference between layers during the recovery stage (p = 0.02; ES = 0.93, 95% CI = −0.11 to 1.99). These results verified that CO₂ worked as a vascular dilator to induce a global increase of blood flow in both scalp/skull and brain tissues.

Fig. 5.

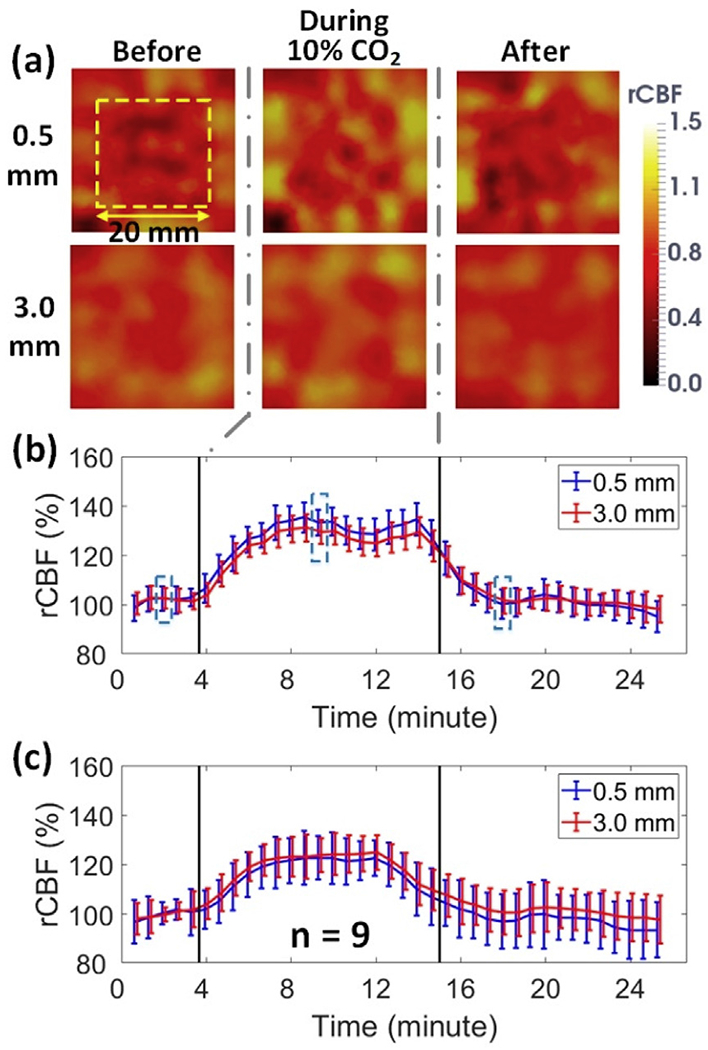
3D imaging of rCBF responses to CO₂ inhalation. (a) Cross-sectional views of 3D flow images at the depths of 0.5mm (scalp/skull) and 3.0mm (cerebral cortex) before, during, and after CO₂ inhalation in an illustrative rat (Rat #5). (b) Time-course of rCBF changes at two depths from Rat #5. Error bars represent standard deviations of regional rCBF. (c) Average time-course rCBF variations over 9 rats. Error bars represent standard errors of regional rCBF over 9 rats.

3.3. CBF responses in rats during unilateral and bilateral CCA ligations

Fig. 6a and Fig. 6b show typical 2D blood flow maps in a rat (Rat #3) and the corresponding time-course for rCBF across different phases of CCA ligations, including baseline, left-ligation, bilateral-ligation, and the release of right-ligation. Fig. 6c displays average time-course changes in rCBF over 8 rats. Table 2 summarizes rCBF changes and corresponding p and ES (with 95% CI) values at different phases of ligations. Significant differences in rCBF from baseline were observed in both the left and right hemispheres at all stages of ligations (p ≤ 0.01). The unilateral (left) ligation and the recovery stage (release of right ligation) resulted in significantly different rCBF responses between the two hemispheres (p ≤ 0.002). All of these significant differences had large ES (Table 2). rCBF was not significantly different between the two hemispheres during the bilateral ligation (p = 0.051).

Fig. 6.

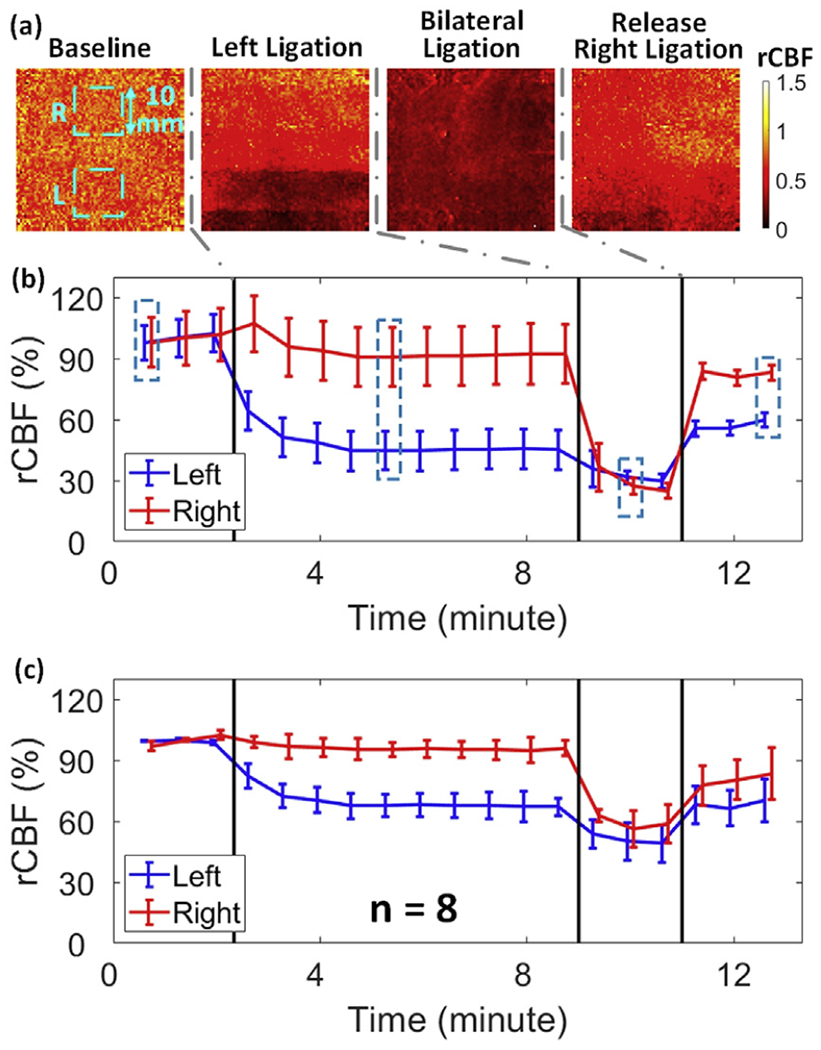
2D mapping of rCBF responses to sequential unilateral and bilateral CCA ligations. (a) 2D rCBF maps before, during, and after unilateral and bilateral ligations in an illustrative rat (Rat #3). The 10 × 10mm² regions used to average CBF values corresponding to each hemisphere are marked with dashed squares. (b) Time-course of rCBF variations in two hemispheres from Rat #3. Error bars represent standard deviations of regional rCBF. (c) Average time-course of rCBF variations in each hemisphere for 8 rats. Error bars represent standard errors of regional rCBF over 8 rats.

Table 2.

rCBF changes during unilateral and bilateral CCA ligations compared to their baselines (100%) over 8 rats. Bolded differences are insignificant.

	8 Rats		Left Ligation	Bilateral Ligation	Release Right Ligation
2D Maps	Left		69 ± 4% p < 10−3; ES = 7.01 (4.15, 9.88)	50 ± 5% p < 10−3; ES = 9.82 (5.94, 13.70)	66 ± 5% p < 10−3; ES = 6.21 (3.62, 8.79)
	Right		95 ± 3% p = 0.01; ES = 1.15 (0.01, 2.31)	56 ± 5% p < 10−3; ES = 7.71 (4.59, 10.82)	80 ± 6% p < 10−3; ES = 3.31 (1.66, 4.96)
	Between Hemispheres		p < 10−3; ES = 4.21 (2.28, 6.13)	p = 0.051; ES = 0.78 (−0.32, 1.90)	p = 0.002 ES = 1.52 (0.30, 2.74)
3D Images	0.5 mm Layer	Left	85 ± 3% p < 10−3; ES = 5.14 (2.91, 7.37)	61 ± 7% p < 10−3; ES = 5.39 (3.08, 7.70)	62 ± 9% p < 10−3; ES = 4.09 (2.20, 5.98)
		Right	95 ± 4% p = 0.06; ES = 1.01 (−0.12, 2.15)	58 ± 7% p < 10−3; ES = 5.89 (3.41, 8.37)	93 ± 8% p = 0.054; ES = 0.81 (−0.29, 1.93)
		Between Hemispheres	p < 10−3; ES = 3.09 (1.50, 4.68)	p = 0.45; ES = 0.26 (−0.81, 1.34)	p < 10−3; ES = 4.16 (2.25, 6.07)
	3.0 mm Layer	Left	35 ± 9% p < 10−3; ES = 7.09 (4.19, 9.98)	32 ± 11% p < 10−3; ES = 6.04 (3.51, 8.57)	41 ± 12% p < 10−3; ES = 4.56 (2.52, 8.59)
		Right	84 ± 6% p < 10−3; ES = 2.61 (1.15, 4.07)	34 ± 10% p < 10−3; ES = 6.05 (3.52, 8.59)	84 ± 11% p = 0.003; ES = 1.42 (0.22, 2.62)
		Between Hemispheres	p < 10−3; ES = 4.50 (2.48, 6.52)	p = 0.56; ES = 0.20 (−0.87, 1.27)	p < 10−3; ES = 2.22 (0.85, 3.58)
	Between Layers	Left	p < 10−3; ES = 5.49 (3.15, 7.84)	p < 10−3; ES = 2.22 (0.86, 3.59)	p = 0.007; ES = 1.25 (0.08, 2.43)
		Right	p < 10−3; ES = 2.27 (0.89, 3.64)	p < 10−3; ES = 2.00 (0.68, 3.31)	p = 0.03; ES = 2.22 (0.85, 3.58)

Fig. 7a shows the cross-sectional views of 3D images at the depths of 0.5 mm and 3.0 mm, reconstructed from the same rat (Rat #3). As stated, these two depths (0.5 mm and 3.0 mm) beneath the head skin represent the tissues in the scalp/skull and cerebral cortex, respectively. The time-course of changes in rCBF over different phases of ligations in both layers of each hemisphere is illustrated for Rat #3 (Fig. 7b) and for all 8 rats (Fig. 7c). The summary of rCBF changes in different layers of each hemisphere is also included in Table 2. As expected, sequential CCA ligations (i.e., left ligation followed by bilateral ligation) resulted in stepwise rCBF decreases in the corresponding ligated hemisphere(s). Significant changes in rCBF were found at all stages of ligations in both layers of the ligated hemisphere(s) (p < 10⁻³). In contrast, there were no significant changes in the surface layer of the contralateral (right) hemisphere during stages of unilateral (left) ligation (p = 0.06 and p = 0.054), likely due to the collateral circulation through the Circle of Willis. However, significant rCBF decreases were observed in the deep layers of the right hemisphere (p < 10⁻³) during bilateral ligations, indicating global ischemia. Moreover, significant rCBF differences were observed between the two hemispheres during the unilateral ligation and recovery stages (p < 10⁻³) and between the two layers (p ≤ 0.03). All the observed significant differences had large ES (Table 2). As with the 2D image analysis, rCBF was not significantly different between the two hemispheres during bilateral ligation when analyzed from 3D images at either depth (p = 0.45 and p = 0.56).

Fig. 7.

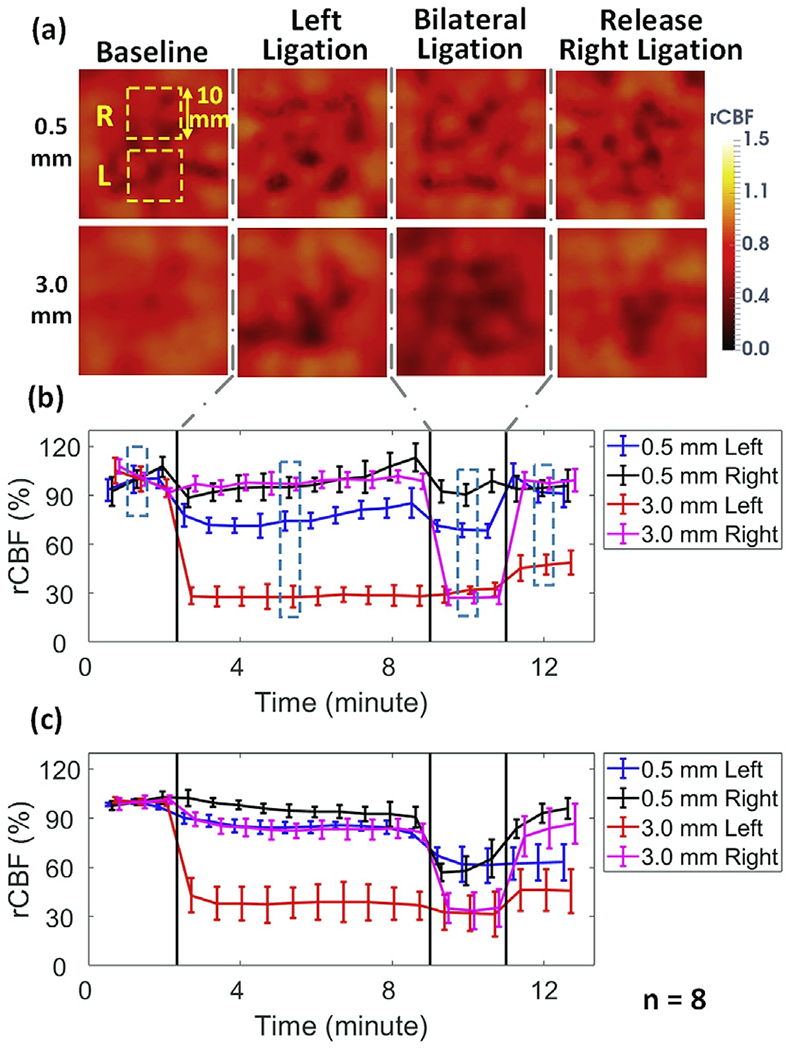
3D imaging of rCBF responses to sequential unilateral and bilateral CCA ligations. (a) Cross-sectional views of 3D flow images at the depths of 0.5mm (scalp/skull) and 3.0mm (cerebral cortex) before, during, and after unilateral and bilateral ligations in an illustrative rat (Rat #3). The 10 × 10mm² regions used to average CBF values corresponding to each hemisphere are marked with dashed squares. (b) Time-course of rCBF variations in two hemispheres from Rat #3. Error bars represent standard deviations of regional rCBF. The dashed boxes represent the time of the images in Fig. 7a. (c) Average time-course of rCBF variations in two hemispheres over 8 rats. Error bars represent standard errors of regional rCBF over 8 rats.

3.4. Longitudinal CBF responses to unilateral MCAO in a rat

3D images of CBF variations in a rat (Rat #10) before, during, and 14 days after 60-min unilateral MCAO were reconstructed using the same method described above (data not shown). Fig. 8 shows the time-course of rCBF changes before, during, and after MCAO-induced stroke in two layers (0.5mm and 3.0 mm) for each hemisphere. Substantial rCBF decreases were observed in the two layers of ipsilateral side after inserting the filament into left internal carotid artery, especially in the brain layer (−70%). After withdrawing the filament, rCBF recovered gradually toward its baseline. From 9 to 14 days after stroke, rCBF values in different layers of two hemispheres tended to be similar, although they were still lower than the pre-stroke values.

Fig. 8.

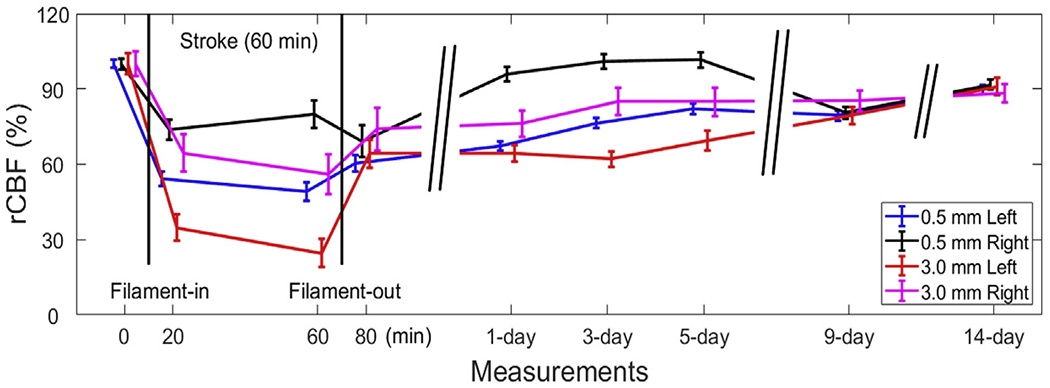
Longitudinal monitoring of rCBF responses to unilateral MCAO. Time-course of rCBF changes at the depths of 0.5mm (scalp/skull) and 3.0mm (cerebral cortex) of both hemispheres in a rat (Rat #10) before, during, and until 14 days after MCAO-induced stroke in the left hemisphere. Error bars represent standard deviations of regional rCBF.

4. Discussion and conclusions

We have modified, optimized, and tested a fully noncontact scDCT system that allows for noninvasive, continuous, and longitudinal imaging of CBF variations in rat brain through intact scalp and skull (Fig. 1). In scDCT, a galvo mirror is used to remotely and rapidly project point NIR light to different source positions and an EMCCD camera with numerous pixels/detectors is used to detect boundary diffuse speckle contrasts resulting from motion of red blood cells (i.e., CBF). The focused NIR point source illuminations facilitate relatively deep probing into rat brain through intact scalp and skull. In addition, thousands of parallel pixels/detectors provided by the EMCCD camera significantly improve SNRs (via averaging pixels/detectors) and temporal/spatial resolution, and greatly reduce device cost and dimensions. The scDCT measurement allows a fully noncontact scheme, avoiding the difficulties of fiber-optic probe installation on a small rat head and eliminating potential disturbances in cerebral hemodynamics due to probe contact. The noninvasive, noncontact, and easy-to-operate capability of scDCT is particularly useful for continuous, frequent, and longitudinal cerebral monitoring. Moreover, scDCT works in the reflectance configuration with an adjustable ROI, rapid and robust data acquisition, and flexible S-D arrangements. The reflectance-based operation increases the applicability of scDCT to large subjects (e.g., human neonates) where transmission is not feasible, thereby promoting translatability between small animals and human subjects.

The scDCT system has been optimized for continuous cerebral imaging in rats. To image a rat head with a small detection area (20 × 20mm²), an adjustable iris diaphragm was added into the source path to optimize the intensity and spot size of incident light. To balance temporal and spatial resolution, reduce computation time, and achieve sufficient SNRs, the numbers of sources and detectors were optimized for 2D and 3D imaging. In 3D reconstruction, we optimized the parameters/configuration in NIRFAST, including medium filter, mesh/node size, regularization value, and stopping criteria. In 2D mapping, we averaged boundary data collected at the effective S-D separations of 2–8mm to generate a 2D map over a depth up to ~4mm (i.e., approximately one half of the S-D separation).

To calibrate the modified scDCT system, homogenous Intralipid phantoms were used to optimize camera exposure time and determine effective S-D separations with the expectation that Intralipid particle flow was uniform in the liquid solution (Fig. 3). The scDCT technique inherits the concept of LSCI for blood flow measurements on a tissue surface. A previous study has experimentally compared measurement sensitivities and SNRs of LSCI with exposure times ranging from 1 to 20 ms (Yuan et al., 2005), and verified the optimal exposure time of 5 ms. Similarly, we have compared our scDCT measurement results in homogenous tissue phantoms at exposure times of 1, 2, and 5 ms (see Supplementary Fig. 1). Data obtained with the exposure time of 5 ms generate the most stable/constant relative flow values at effective S-D separations of 2–8 mm. To test the dependence of effective S-D separations on phantom optical properties, we used the scDCT to measure particle flow changes due to varied temperatures (Supplementary Fig. 2a) and varied tissue absorption coefficient μ_a by adding Indian ink (Supplementary Fig. 2b). All results shown in Fig. 3 and Supplementary Figures verify that data obtained at S-D separations of 2–8 mm are constant and stable.

The larger flow variation observed at shorter S-D separations of <2 mm is likely due to the violation of photon diffusion approximation. The greater flow variation observed at larger S-D separations of >8mm is likely due to lower level of SNRs (with lower light intensities detected). Using boundary data at short S-D separations of 2–8mm may cause reconstruction errors due to violation of photon diffusion approximation in NIRFAST. However, our results in phantom tests (Fig. 3) and in vivo studies (Figs. 5 and 7) demonstrate the success of scDCT in 3D reconstruction of flow distributions. In addition, previous studies with conventional DCT or SCOT have also used short S-D separations of 2.7–10mm (Culver et al., 2003) or 0.5–3mm (Dragojević et al., 2017) for 3D imaging of CBF distributions in rats or mice.

After calibrating the modified scDCT system using standard tissue-simulating phantoms (Fig. 3), we tested the capability and sensitivity of scDCT for continuous and longitudinal monitoring of global/regional cerebral hyper-perfusion/hypo-perfusion and post-operation recovery in rats undergoing transient cerebral hyperemia (via CO₂ inhalation) and cerebral ischemia (via CCA ligations or MCAO). The 10% CO₂ inhalation induced significant increases in rCBF from the baseline of 100% of 15% (115 ± 7%) in 2D maps and 18% (118 ± 8%) and 19% (119 ± 8%) in the superficial (scalp/skull) and deep (brain) layers of 3D images, respectively (Figs. 4 and 5, and Table 1). These results are expected in a healthy population, as the increased CO₂ induces cerebrovascular dilation, leading to a global increase in blood flow all over the head. The small variation in rCBF increases between the results in 2D and 3D images (from +15% to +19%) was likely due to differences in methodology (i.e., 2D versus 3D).

Previously, 10% CO₂ inhalation induced a 47 ± 11% CBF increase in 7 rats measured by arterial-spin-labeling (ASL)-MRI (Sicard et al., 2003) and a 35.1 ± 6.3% CBF increase in 11 rats measured by laser Doppler flowmetry (LDF) (Wolk et al., 1995). Another study using diffuse correlation spectroscopy (DCS) found an ~25% CBF increase in 7 rats with a continuous inhalation of 5%–7.5% CO₂ for ~10 min (Carp et al., 2010). We found in the present study that 10% CO₂ inhalation for 10 min induced a 19 ± 8% CBF increase in 9 rats (Table 1). The CBF responses to CO₂ inhalation measured by the DCS (~+25%) and scDCT (~+19%) are similar. Comparing to measurements by ASL-MRI (~+47%) and LDF (~+35%), an underestimation of CBF increases by DCS and scDCT (<~25%) was likely due to partial volume effects from the overlaying skull (lack of blood flow) on CBF measurements. In the future, we will explore optimizing 3D reconstruction algorithms (e.g., adding sensitivity correction factors along depths) to further reduce this effect/artifact (Tian and Liu, 2014). Moreover, we will implement blood gas tests in our future studies to further verify CBF measurement results. However, our noninvasive and portable scDCT has obvious advantages over ASL-MRI (large and expensive instruments) as well as LDF and DCS (spectroscopic measurements with invasive retraction of scalp/skull).

The capability of scDCT for continuous imaging of regional rCBF variations was then examined in rats undergoing sequential unilateral and bilateral CCA ligations. The unilateral left-CCA ligation created significant decreases in ipsilateral (left) rCBF from the baseline of 100% of 31% (to 69 ± 4%) in 2D maps and 15% (to 85 ± 3%) in the superficial layer (scalp/skull) and 65% (to 35 ± 9%) in the deep (brain) layer of 3D images (Figs. 6 and 7, and Table 2). The sequential bilateral CCA ligation induced greater decreases in rCBF: 50% (to 50 ± 5%) and 44% (to 56 ± 4%) within the left and right hemispheres, respectively, in 2D maps. Similar left and right hemispheric rCBF decreases were measured from 3D images: 39% (to 61 ± 7%) and 35% (to 65 ± 10%) in the superficial layer (scalp/skull) and 68% (to 32 ± 11%) and 66% (to 34 ± 10%) in the deep (brain) layer. Our reconstructed 3D images covered depths spanning from superficial skull and scalp to deeper cerebral cortex. Since the top layers of skull and scalp were less affected by the CCA ligations due to collateral supply from the vertebral artery, smaller CBF decreases were observed in the top scalp/skull layer compared to the deeper brain layer. Compared to 3D reconstruction results, 2D mapping resulted in an underestimation of rCBF responses in deep brain tissues and an overestimation in top scalp/skull tissues (i.e., partial volume effects). This is not surprising as results from 2D mapping are overlapped mixture signals from the top scalp/skull to the deeper brain. Partial volume effects were also observed in 2D mapping of CBF responses in the control (right) hemisphere without ligation (Table 2). Nonetheless, significant rCBF differences were observed between the two hemispheres in both 2D maps and 3D images and between the two layers in 3D images, indicating the sensitivity of scDCT in detecting regional cerebral hypoperfusion and recovery.

A few studies using LDF (Alkayed et al., 1998; Takahashi et al., 1997) or conventional DCT (Culver et al., 2003) have monitored CBF reductions in rats with acute cerebral artery occlusions. Previously using LDF, Alkayed et al. and Takahashi et al. found that CBF levels were reduced during acute MCAO from 100% baseline to 18.9 ± 1.4% in 22 rats and 20.8 ± 7.7% in 5 rats, respectively (Alkayed et al., 1998; Takahashi et al., 1997). Using a convetional DCT system, Culver et al. found that CBF levels were reduced from 100% baseline to 42 ± 4% in 5 rats during acute MCAO (Culver et al., 2003). In the present study with scDCT, we observed CBF reductions of ~65% (to 35 ± 9%) in 8 rats during acute unilateral CCA ligation and 70% in one rat during acute MCAO (see Figs. 6–8 and Table 2). Note that both unilateral CCA ligation and MCAO cut off the CBF in one hemisphere of brain. In summary, the observed CBF reductions due to acute arterial occlusions were ~80% (LDF), ~65–70% (scDCT), and ~60% (conventional DCT). It is not surprising that LDF detected the greatest CBF reduction (80%) as the probe was installed directly on the cerebral cortex where the most severe ischemia occurred (eliminating any partial volume effects). Comparing to conventional DCT with limited numbers of sources and detectors (Culver et al., 2003), our scDCT with higher sampling densities provided by the EMCCD camera generated results with less partial volume effects from the overlaying scalp and skull on CBF measurements. Overall, our fully noninvasive scDCT achieved a similar level of sensitivity/accuracy in detecting CBF reductions in ischemic rat brains as other conventional techniques such as LDF and DCT, which require invasive scalp retraction.

The last experiment was designed to test the capability of scDCT for longitudinally monitoring CBF variations in a rat undergoing unilateral MCAO and long-term recovery after acute stroke. A substantial decrease in rCBF (70%) was observed in the brain layer of the ipsilateral hemisphere during a unilateral 60-min MCAO (Fig. 8). After withdrawal of the filament to restore cerebral perfusion, rCBF recovered gradually towards pre-stroke baseline over a period of 14 days, although it remained somewhat lower than its pre-stroke value. Differences in rCBF responses were observed between the two hemispheres and two layers over the monitoring period, indicating the sensitivity and stability of scDCT for longitudinal detection of regional cerebral hypoperfusion and recovery. The trend of rCBF recovery after stroke agrees with that measured by ASL-MRI in rats (Seevinck et al., 2010). In addition, CBF variations over the monitoring period were also associated with neurological/behavior changes. The rat demonstrated the most severe neurological deficit symptoms one day after stroke, including stiffness of forelimb and mild coordination dysfunction. The rat recovered gradually in the first week after stroke and behaved normally at post-stroke Day 14. Noninvasive and noncontact measurements with scDCT significantly reduce interference with cerebral hemodynamics and make it easy to implement for frequent and longitudinal monitoring.

As expected, 2D mapping of CBF required less computation time (e.g., ~10 s in this study), but was subject to partial volume effects from overlaying layers of scalp and skull tissues. By contrast, 3D tomography of CBF reduces partial volume effects, but needs a longer reconstruction time (e.g., ~15 min in this study). Our data shown in Fig. 7 and Table 2 support this statement. For example, CBF reductions during bilateral CCA ligations were 66% (left) to 68% (right) in the brain layers (at the depth of 3 mm) of 3D images, which were greater than the reductions of 44% (left) to 50% (right) observed in 2D maps. Note that 2D maps of CBF were calculated in this study via averaging boundary data at multiple effective S-D separations of 2–8 mm, thus representing a mixture of signals from the superficial scalp/skull to the deep brain. Therefore, our 2D mapping method is different from the traditional LSCI technique, which uses wide-field illumination and provides 2D maps of CBF only from superficial tissues (penetration depth < 1 mm).

We note that our innovative scDCT system can be further improved in the future and extended for other applications. For example, use of a high-quality CCD or scientific complementary metal–oxide–semiconductor (sCMOS) camera with fast sampling rate and high sensitivity would improve data acquisition, detection sensitivity, and probing depth. The algorithms for 2D mapping and 3D reconstruction may be optimized to be faster (Wu et al., 2015) and more robust (e.g., with depth compensation for denoise) (Tian and Liu, 2014; Tian et al., 2010). We may also explore absolute BFI measurements by using multiple exposure times of the camera and/or multiple S-D separations (Liu et al., 2017; Valdes et al., 2014). Adding other long-coherence laser diodes at different NIR wavelengths would allow for simultaneous imaging of blood flow and oxygenation distributions (Seong et al., 2016; Shang et al., 2009).

In conclusion, we have downscaled, optimized, and tested an innovative scDCT system for noninvasive, continuous, and longitudinal imaging of CBF distributions in rat brains through intact scalp and skull. The continuous dynamic imaging capability of the system was proven by imaging global CBF increases during CO₂ inhalations and regional CBF decreases during CCA ligations. The regional imaging capability was demonstrated by imaging CBF distributions across two hemispheres of the brain during sequential unilateral and bilateral CCA ligations. The longitudinal imaging capability was shown by imaging CBF variations over a long recovery period of 14 days after MCAO-induced stroke. Both 2D and 3D images capture temporal CBF variations precisely. Compared to the 2D mapping method, the 3D imaging method reduces partial volume effects, but needs more computation time for image reconstruction. Moreover, our results generally agree with those reported using other CBF monitoring techniques in rats with similar experimental protocols. Our innovative scDCT system provides many unique advanced features including fully noncontact hardware, rapid data acquisition, adjustable S-D patterns/density over a flexible ROI/FOV, FEM-based image reconstruction, and a simple low-cost instrument. Most importantly, scDCT allows for probing depths up to ~10mm (Huang et al., 2015a, 2017), which is sufficient for transcranial brain measurements in small animals (e.g., mouse, rat, piglet) and human neonates, who have relatively thinner skulls (Li et al., 2015; O’Reilly et al., 2011). Ultimately with more future investigations, we expect to provide a unique, noninvasive, noncontact cerebral imager for basic neuroscience research in small animal models and translational studies in human neonates.