Abstract
Mathematical models have a long history in epidemiological research, and as the COVID-19 pandemic progressed, research on mathematical modeling became imperative and very influential to understand the epidemiological dynamics of disease spreading.
Mathematical models describing dengue fever epidemiological dynamics are found back from 1970. Dengue fever is a viral mosquito-borne infection caused by four antigenically related but distinct serotypes (DENV-1 to DENV-4). With 2.5 billion people at risk of acquiring the infection, it is a major international public health concern. Although most of the cases are asymptomatic or mild, the disease immunological response is complex, with severe disease linked to the antibody-dependent enhancement (ADE) - a disease augmentation phenomenon where pre-existing antibodies to previous dengue infection do not neutralize but rather enhance the new infection. Here, we present a 10-year systematic review on mathematical models for dengue fever epidemiology. Specifically, we review multi-strain frameworks describing host-to-host and vector-host transmission models and within-host models describing viral replication and the respective immune response.
Following a detailed literature search in standard scientific databases, different mathematical models in terms of their scope, analytical approach and structural form, including model validation and parameter estimation using empirical data, are described and analyzed.
Aiming to identify a consensus on infectious diseases modeling aspects that can contribute to public health authorities for disease control, we revise the current understanding of epidemiological and immunological factors influencing the transmission dynamics of dengue. This review provide insights on general features to be considered to model aspects of real-world public health problems, such as the current epidemiological scenario we are living in.
Keywords: Mathematical models, Dengue fever, Multi-strain, Vector-host, Within-host, Antibody dependent-enhancement
Abbreviations: TCI, Temporary Cross-Immunity; ADE, Antibody-Dependent Enhancement
1. Introduction
Mathematical models have a long history in epidemiological research. As formal frameworks to convey ideas about the components of a host-(vector)-pathogen interactions, epidemic models act as a tool to understand and to predict infectious disease dynamics under various conditions, and are often used to evaluate the impact of public health intervention measures for disease control.
Mathematical models describing dengue fever epidemiological dynamics are found back from 1970 [1]. Dengue fever is one example of a viral mosquito-borne infection, a major international public health concern. Most of the cases are asymptomatic or mild. Caused by different serotypes with severe disease linked to the Antibody-Dependent Enhancement (ADE), a disease augmentation phenomenon where pre-existing antibodies do not neutralize but rather enhance the new infection.
With well-known complex epidemiological dynamics, mathematical models for dengue fever try to incorporate factors focusing on several different aspects of the disease and vectors, which can imply rich dynamic behavior even in the most basic dynamical models. The existing models are developed to evaluate, for example, the effect of co-circulation of multiple strains (or variants), the immunological path for disease severity, and the impact of vaccination, similar to what is now known about COVID-19 epidemiology.
Following a review on dengue models to assess the impact of future dengue vaccines published in 2011 [2], a careful review of deterministic dengue modeling was published in 2012 [3], where two main approaches were considered, the vector-host and the host-to-host transmission models. Both reviews studied a collection of papers proposing different structural approaches and parameter assumptions to describe dengue epidemiological dynamics as well as the impact of the available intervention measures for disease control. However, those papers date back from 2012 and an updated revision of the state-of-the-art is timely.
1.1. Dengue fever epidemiology
Transmitted to humans through the bites of infected female Aedes mosquito [4], [5], dengue fever is a major public health problem, with more than one-third of the world population being at risk of acquiring the disease [5], [6]. Caused by four antigenically distinct but related viruses, named DENV-1 to DENV-4 serotypes [7], [8], [9], dengue infection can result in a wide range of clinical manifestations, ranging from inapparent (asymptomatic) and mild disease (an acute febrile viral disease frequently presenting with headaches, bone or joint and muscular pains as symptoms), to a severe and occasionally fatal hemorrhagic clinical picture [5], [10]. Modeling estimate indicates that over 390 million dengue infections occur every year, of which 96 million manifest symptoms with any level of disease severity [11].
While primary natural dengue infection is often asymptomatic, a secondary dengue infection with a heterologous serotype is considered the main risk factor for developing a severe form of the disease [12], [13], [14], [15]. Individuals infected with one serotype maintain a life-long protective immunity to infection by the homologous virus, but protective immunity to infection with heterologous serotypes is only temporary [16]. When the short-term cross-protection wanes, patients experiencing a secondary heterologous dengue virus infection are at higher risk of severe disease [15], [17], [18], [19], [20], [21], [22], via the so-called ADE process [15], [18], [21], [23], [24]. The ADE theory postulates that a heterotypic virus causing a secondary dengue infection is recognized by antibodies produced during the first infection. Instead of neutralizing the new dengue serotype, the pre-existing antibodies promote the enhancement of the infection by facilitating the entry of the complex antibody-heterologous virus into target cells. This disease augmentation phenomenon and its occurrence in dengue has been used to explain the etiology of severe disease [15], [25], [26], [27], which has been shown to be correlated with higher viral loads [28], [29], [30], [31], [32], [33], [34].
There is no specific treatment for dengue infection. While uncomplicated dengue cases involve only supportive care, severe dengue cases require hospitalization. Due to the dengue-specific complexities described above, vaccine development focuses on the generation of a tetravalent vaccine aimed at providing long-term protection against all dengue virus serotypes [35]. A safe, effective and affordable dengue vaccine against the four strains would represent a significant advance for the control of the disease and could be an important tool for reducing disease transmission and mortality.
Several candidate tetravalent vaccines are at various stages of development [36], [37]. Two tetravalent dengue vaccines have now completed phase 3 clinical trials: Dengvaxia [38], [39], [40], a product developed by Sanofi Pasteur that is now licensed in more than 20 countries, and the DENVax vaccine, developed by Takeda Pharmaceutical Company [41], [42], [43].
In mid-April 2016, the World Health Organization's Scientific Advisory Group of Experts on Immunization (SAGE) recommended the use of the Dengvaxia vaccine in individuals aged 9-45 years in highly endemic populations [44], based on a mathematical modeling exercise evaluating the impact of this vaccine administration [45]. Two large mass vaccination programs were implemented, in the Philippines and Brazil, with 1 million children and adolescents vaccinated without any pre-vaccination testing. Dengvaxia resulted in a higher rate of hospitalized severe dengue cases when given to seronegative children, compared with age-matched seronegative controls [40], with the risks of Dengvaxia administration being extensively discussed [46], [47], [48], [49], [50]. Following the long-term safety data stratified by serostatus [51], a new recommendation by the World Health Organization (WHO) was published [52], [53] proposing a screening test prior to vaccination to restrict vaccine administration to seropositive individuals only [36].
As for the DENVax vaccine, efficacy against virologically confirmed dengue disease and hospitalization was shown to be more balanced between seronegatives and seropositives [41], [42], however, similar to what was observed for Dengvaxia, the individual serostatus prior to vaccination is also a determinant for vaccine efficacy [43]. Recent results have shown that vaccine efficacy continues to decrease over time [43], [54], and hence, long-term surveillance consisting of prudent and careful observation of the DENVax vaccine phase 3 recipients is required.
In the absence of an effective and safe dengue vaccine, vector control remains the only alternative to prevent dengue transmission. Epidemic models are often used as guiding tools for decision-making, but what is the value of such tools in the public health context?
1.2. Mathematical models for dengue fever
Developing new mathematical tools to guide public health strategies for control of dengue transmission is challenging. Very complicated models are often developed to understand the dynamics of transmission of infectious diseases. However, due to the high degree of correlation between parameters, the evaluation of the results becomes difficult. Even though using the appropriate statistical methods and model techniques to provide optimal guidance for disease control, modelers are often lost with the amount of “realistic assumptions” required to be included in the modeling framework (by the field, clinical and public health workers), and the frequent lack of appropriate data needed to evaluate disease dynamics.
Huge modeling efforts focusing on dengue control strategies have been performed in the past 10 years. Rather than being an extensive history of dengue transmission models, this paper will present a systematic review of multi-strain modeling approaches for dengue transmission and control. Following a detailed literature search in standard databases, we describe different mathematical models in terms of their scope, mathematical approach and structural form, including model validation and parameter estimation using empirical data. Besides different epidemiological aspects involved in dengue transmission, we present a detailed description of the mathematical frameworks recently published, aiming to identify a consensus on infectious diseases modeling aspects that can contribute to public health authorities' capacity for implementing intervention measures for disease control.
2. Material and methods
2.1. Search terms and databases
This review was carried out between May and November 2021. We have used four distinct databases, PubMed, Web of Knowledge, Mendeley and ScienceOpen, to search for scientific papers dealing with mathematical models developed for dengue fever disease. In each database, the keywords “dengue models”, “multi-strain dengue model”, “two strain dengue model”, and “multi-strain epidemic models” were systematically used.
2.2. Inclusion and exclusion criteria
The following inclusion criteria were used: (i) Full-text peer-reviewed published articles describing host-to-host, vector-host, and within-host modeling frameworks applied to dengue fever epidemiological dynamics, published from 2010 up to June 2021. (ii) Deterministic, stochastic, and spatial modeling approaches. (iii) Studies using (or not using) empirical data for model parametrization and model validation. (iv) Multi-strain models dealing with intervention measures for dengue control, i.e., vector control, vaccination, or both combined. The following exclusion criteria were applied: (i) For vector-host or host-to-host structural approaches, single-serotype models were excluded since they were not epidemiologically relevant to explain the immunopathogenesis of severe disease. For that, at least two infections caused by different dengue serotypes were needed to be considered in the modeling framework. (ii) Research articles solely on virology, immunology, or entomology without containing a multi-strain modeling framework to describe either dengue transmission dynamics or dengue control strategies at the population level or within-host dengue immunological responses were also excluded.
2.3. Model features and selection
The search and selection process is shown in Fig. 1 . Research papers obtained from the search and selection process described above were assessed, and models features were identified, as shown in Table 1 . The following modeling features were collected manually in an Excel matrix for vector-host, host-to-host, and within-host frameworks: deterministic, stochastic, or spatial approaches; with or without data validation/parametrization; with or without disease control, i.e., vector control, vaccine, or both, including optimal control, and other features, such as seasonality or co-infection.
Fig. 1.
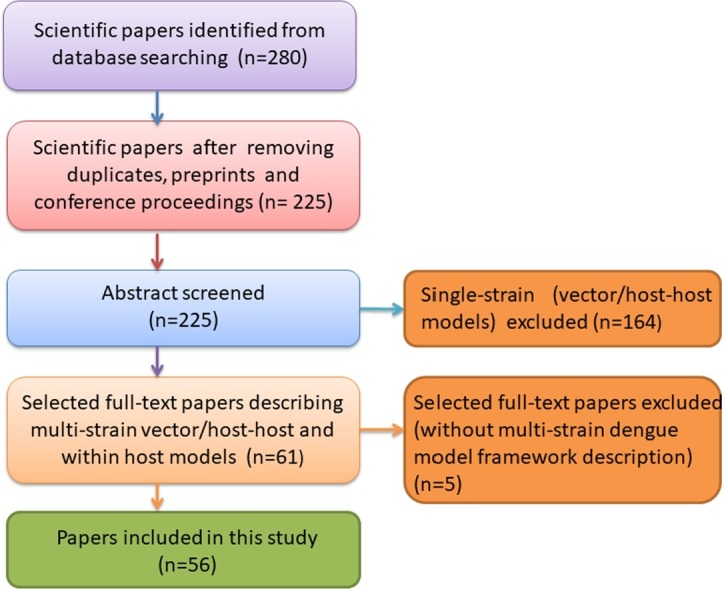
Schematic flow diagram for the selection process with inclusion and exclusion criteria. PubMed, Web of Knowledge, Mendeley and ScienceOpen databases were used to search for scientific papers dealing with mathematical models applied to dengue fever epidemiology.
Table 1.
Comparison of modeling features in selected research papers for vector-host, host-to-host and within-host frameworks included in this review.
From all four databases, 280 full-text articles describing single- and multi-strain frameworks for vector-host, host-host and within-host models were obtained. Duplicates, preprints and conference proceedings articles were excluded. A total of 225 abstracts were screened, and 164 papers dealing with single-serotype vector-host and single-serotype host-to-host models were excluded. An exception for the multi-strain selection criteria was applied to within-host modeling framework that often does not consider serotype stratification. Nevertheless, within-host dynamical models are of major importance to evaluate the impact of imperfect vaccines, and such framework was not included in the most recent review papers on dengue models. Among the remaining 61 selected papers, 5 did not contain a model framework for dengue specifically and were later excluded as well.
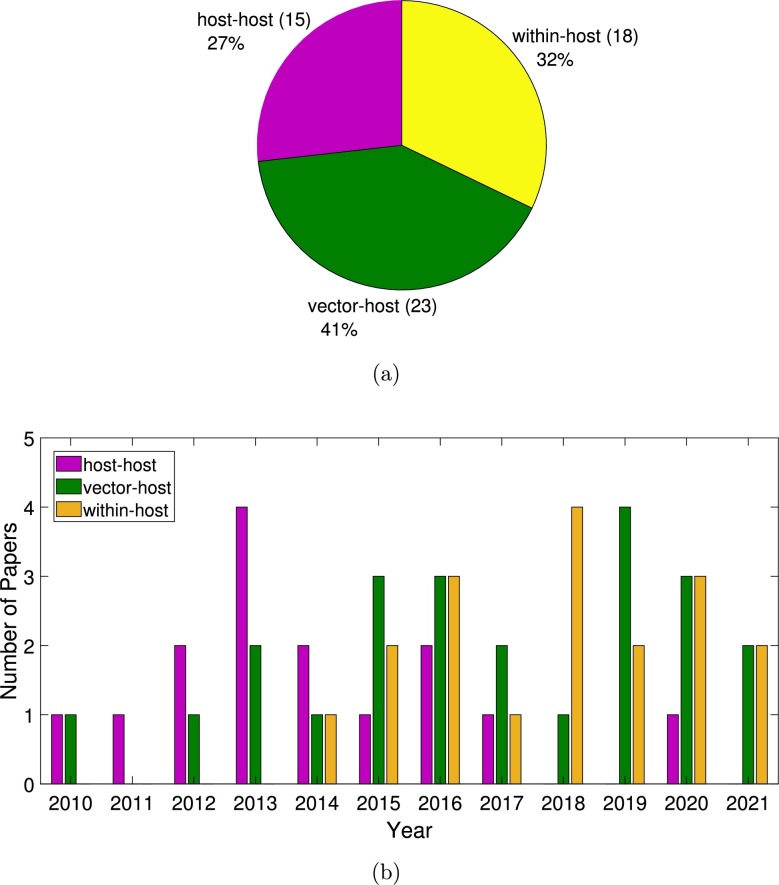
Following the inclusion and exclusion criteria above, a total of 56 articles were included in this study, covering research on multi-strain host-to-host models (15 papers), multi-strain vector-host models (23 papers) and within-host models (18 papers) that were published between January 2010 and June 2021.
3. Results
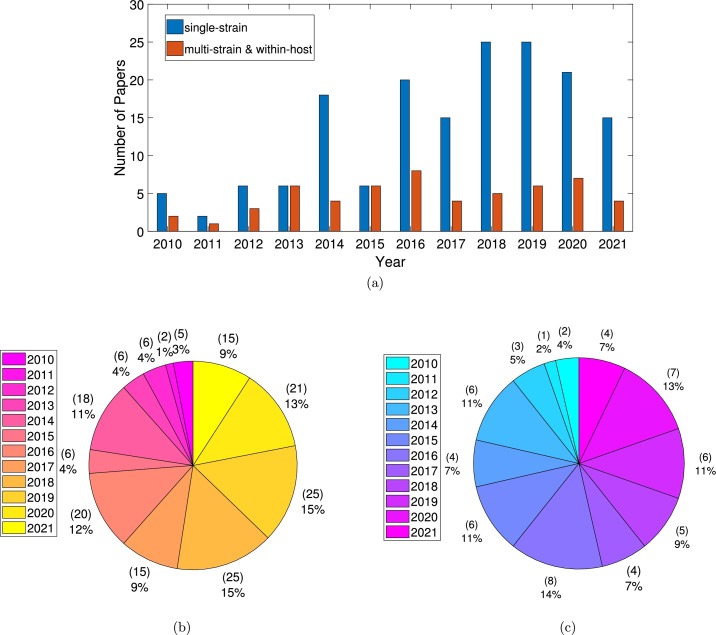
Although the number of models developed to understand the dynamics of dengue transmission at population and at within-host levels has increased during the last decade, most of the published papers were using a single-serotype framework, as shown in Fig. 2 a). The distribution of the listed papers per year is shown in Fig. 2 b), for single-serotype models, and in Fig. 2 c), for multiple-serotype and within-host models. The distribution of the selected papers included in this study is shown in Fig. 3 , with host-to-host models plotted in pink, vector-host models plotted in green, and within-host models plotted in yellow. Note that more than a half of the papers were published in the last 5 years.
Fig. 2.
(a) Yearly distribution of single-strain models, multi-strain and within-host models. In (b) and in (c) pie-charts for single-strain models and multi-strain/within-host models distribution respectively. In total, 56 (out of 225) papers are considered. That is because 5 papers were excluded only after the full-text papers were assessed in detail.
Fig. 3.
(a) Pie-chart for the distribution of the selected papers included in this review: multi-strain host-to-host models in pink, multi-strain vector-host models in green and within-host models in yellow. In (b) yearly distribution of the papers included in this review.
4. Dynamic models for dengue
Epidemic models of disease transmission are developed to understand patterns of interactions between pathogens and hosts. From a microscopic (within-host dynamics) to a macroscopic (transmission dynamics at population level) perspectives, most of the proposed models try to incorporate factors focusing on several different aspects of the disease (multi-strain structure, cross-immunity period and ADE, co-infection, for example) and some biological aspects of the mosquito vector (biting rate, transmission capacity). Once validated with data, those frameworks are extended to answer questions about the impact of the available control measures making them effective tools for public health decision making.
4.1. Host-to-host transmission models
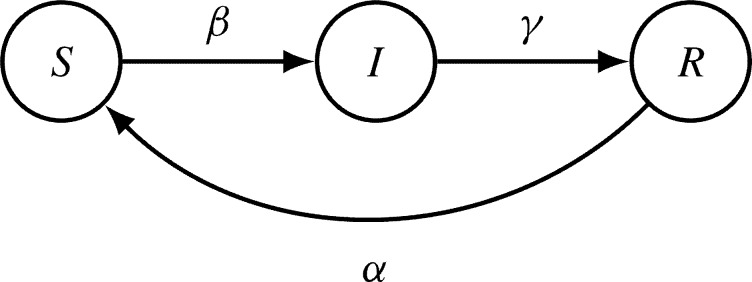
Multi-serotype host-to-host dengue dynamics have been modeled with different extensions of the classical susceptible-infected-recovered (SIR) models, as represented in Fig. 4 .
Fig. 4.
State-flow diagram of a simple epidemiological SIR-type model. The disease-related stages are Susceptible S, Infected I and Recovered R. For a host population of N individuals, the transitions from one to another disease-related state are parameterized by infection rate β, recovery rate γ, and waning immunity rate α.
This approach focuses on the multi-strain aspect of the disease and its effects on the host population, taking effects of the vector dynamics only into account by the effective parameters of the SIR-type model, i.e., seasonality in the infection rate, but not modeling the mosquito dynamics explicitly. Mathematically, that is justified since in vector borne diseases the human hosts' epidemiological dynamics often acts on a much slower time scales than the one of the mosquitoes transmitting the disease, due to their vastly different life spans. To investigate how far the fast time scale of the mosquito life span and its ability to transmit the virus is slaved by the slower human infection immune response dynamics, a model with susceptible (S), infected (I) and recovered (R) humans and susceptible (U) and infected (V) mosquitoes was investigated by Rocha et al. [111]. The authors have shown that the human time scale is the only essential dynamics for the understanding of the available long term data on disease cases, only slightly perturbed by the mosquito dynamics. This analysis of the SIRUV model was qualitatively in agreement with a previously investigated simpler SISUV model, hence a feature of vector-borne diseases in general [112], [113], [114].
Biologically, these findings are of use since the current vector control measures for dengue alone have limited impact, with a successful broad-scale application being difficult to achieve and even harder to be sustained [115]. Therefore, the use of simpler mathematical models to guide how to best integrate interventions against a complicated, multi-strain pathogen with complex transmission dynamics, like dengue, would have important benefits on the practical predictability of the dynamical system [116].
Trying to explain the irregular behavior of dengue epidemics, mathematical models describing the transmission of dengue viruses have focused on multi-strain aspects, ADE and Temporary Cross-Immunity (TCI). A multi-strain mathematical model proposed by Ferguson et al. [117], developed to explore the effect of ADE on dengue transmission dynamics, has shown deterministically chaotic dynamics when strong infectivity of secondary dengue infection was assumed. This model did not consider the cross-immunity period, and co-infection was possible. Therefore, individuals could simultaneously belong to multiple compartments of infection with one and another strain. Chaotic desynchronization in multi-serotype dengue model with ADE was described by Billings et al. [118]. This model also did not include the cross-immunity period, however, cross-infection was not possible as long as an individual was primarily infected. As a result, all compartments were distinct.
Aguiar et al. [119], [120] have investigated a minimalistic two-infection dengue model, an extension of models initially suggested and preliminarily analyzed in [117], [118]. By assuming that a secondary infection could only occur with a different serotype to the one causing the primary infection, the TCI was introduced through additional compartments for individuals recovering from a primary infection, becoming susceptible again after a short cross-immunity period. The addition of a TCI period in such models has shown, for the first time, a new chaotic window in an unexpected and much wider parameter region, including for the reduced infectivity on secondary infection [119], [120]. The restrictive assumption of much higher transmission rates for secondary infections, that was previously necessary to generate complex dynamics resembling the oscillations observed in empirical data, could be relaxed significantly. This finding indicated that deterministic chaos was much more important in multi-strain models than previously thought, opening new ways to analyze the existing data sets.
In 2011, the minimalistic two-infection dengue model proposed by Aguiar et al. [119] was extended by including seasonality to mimic the effect of the vector dynamics [68]. The seasonal model has shown complex dynamics and demonstrated good qualitative agreement between model simulation and empirical data when a short cross-immunity period was combined with the ADE effect, reducing the baseline disease transmission of secondary infections. That assumption was justified by the epidemiological association of increased risk of severe disease observed in secondary infections. The authors have assumed that individuals experiencing a primary dengue infection would become asymptomatic or with mild symptoms, and hence would still be mobile and able to transmit the infection. However, individuals experiencing a second infection with a heterologous serotype would likely develop severe symptoms, being admitted to a hospital, which would decrease their chance to transmit the disease, as compared to primary infected individuals.
Nonetheless, the introduction of stochasticity was needed to explain the fluctuations observed in some of the available dengue data sets, revealing a scenario where noise and complex deterministic skeleton strongly interact [67]. Stollenwerk et al. [66] have revisited the parameter estimation framework for dynamical systems describing biological populations, and have applied it to calibrate the dengue model proposed in [67]. With wide likelihood profiles obtained for some of the parameters, the maximum likelihood iterated filtering technique offers a promising perspective on parameter values inference from dengue cases notifications.
Using bifurcation theory, Kooi et al. [64] have analyzed and compared three multi-strain dengue models proposed in [68], [117], [118], giving insights into the origin of long-term dynamics behavior. Using the same parameter set for all models, the duration of the cross-immunity period and the ADE factor were varied as bifurcation parameters. Besides endemic equilibria and periodic solutions, chaotic behavior originating via different routes were identified. Lyapunov exponent calculation was used to quantify the complex behavior in those models. An interesting dynamical aspect found by Kooi et al. [64] was a torus bifurcation as a route to the chaotic dynamics in the model proposed in [68], a dynamical behavior never described in epidemiology before.
The cross-protection assumption combined with the ADE effect have been modeled in different ways. Despite incorporation of TCI in rather complicated models, the ADE effect would always increase the transmissibility or susceptibility in secondary infections [55], [58], [62], [65], [69]. While Woodall and Adams [61] have assumed partial cross-protection after a primary dengue infection, Reich and colleagues [65] have proposed a model with the enhancement factor acting on individual susceptibility, i.e., assuming that individuals with immunity to one serotype would be more likely to acquire a second infection. By evaluating the fit of their model to the available dengue data from a hospital in Thailand, the authors confirmed that models including short-term cross-protection are better able to fit their data than models without cross-protection. They estimate the optimal length of cross-protection period to be two years. The addition of a serotype-specific transmission rate in their model deteriorates the fitness of the model to data.
The approach proposed by Aguiar et al. in, e.g., [63], [68], [119] combine a short period of temporary cross-immunity between primary and secondary infections, with a second infection contributing less to the force of infection than a primary infection, an assumption justified by disease severity and hospitalization decreasing the human interaction and hence, disease transmission.
A comparison between the basic two-strain dengue model, which captures differences between primary and secondary infections including TCI, with the four-strain dengue model, introducing the idea of competition of multiple strains in dengue epidemics have shown that the combination of TCI period and ADE effect is the most important feature to drive the complex dynamics in the system, more than the detailed number of dengue serotypes to be added in the model [63]. Until that time, the TCI factor was never actively explored, but it is now recognized as an important feature to obtain a realistic dengue model.
The role of the number of subsequent infections versus detailed number of dengue serotypes included in the model framework, and the human immunological aspects associated to disease severity was also discussed in detail by Aguiar et al. [56]. In this survey, extensions of the two infection multi-strain model proposed in [63] are compared, identifying the implications of extra compartments for model dynamics.
The n-strain epidemiological model with primary and secondary dengue infections proposed in [63] can be written as follows
and for serotypes
| (1) |
and for and with
and finally
With chaotic dynamics found to happen in the same parameter region of interest (describing the fluctuations observed in empirical data) for both two- and four-strain models, without significant change in terms of prediction horizon in time series, the minimalistic two-strain model was later extended to include vaccination, and to evaluate the impact of the up-to-date only licensed imperfect dengue vaccine [57].
Although the frequency of tertiary and quaternary dengue infections are low, models assuming third and fourth heterologous infections are often developed. Wikramaratna et al. [69], have constructed a framework to examine the effect of third and subsequent infections on dengue epidemiology, with results indicating that the qualitative nature of the dynamical behavior in models with and without third and fourth infections is predominantly similar.
Many of the multi-serotype models have assumed symmetric infection rates for dengue serotypes. Heterogeneity in serotype transmission rates is discussed in [62]. Authors investigate different transmissions rates among serotypes and have found that asymmetry between serotypes increases the persistence of all strains and that there exists an optimal ADE factor value that maximizes the likelihood of serotype persistence. On the other hand, Kooi et al. [60] have investigated epidemiological asymmetry between the strains, assuming different force of infection rates but keeping all the other epidemiological parameters the same. The robustness of a two-strain symmetric dengue fever model with respect to asymmetry is studied using bifurcation analysis. Results have shown that while in symmetric models the two-strain system is always endemic, in the asymmetric models a one-strain system can also be endemic. Moreover, the asymmetry of the strains stabilizes the long-term dynamics, with chaotic behavior (needed to describe the oscillations observed in empirical data) occurring only for smaller parameter regimes.
A new approach to dengue modeling considering partial cross-enhancement on secondary infection is proposed by Woodall and Adams [61]. Three previously proposed models were modified to include partial cross-enhancement: a base model without TCI [117], a model with stochastic seasonality and co-infection [121], and a vector-host model with cross-temporary class and deterministic seasonality [68]. The authors argue that the enhancement alone is not driving the observed multi-annual oscillations in dengue dynamics, but rather modifying the effects of other drivers. Bosch et al. [58] have used a pattern-oriented modeling (POM) approach to fit and assess a range of dengue models, driven by combinations of temporary cross-protective immunity, cross-enhancement, and seasonal forcing, in terms of their ability to capture the main characteristics of dengue dynamics. The authors have found that to reproduce the patterns in a low seasonality setting, a larger cross-protection period is needed, while in a setting of strong seasonal forcing, an ADE parameter is required.
Regarding the evaluation of control measures, Pandey and Medlock [59] have developed standard SIR-type deterministic dengue models to explore short- and long-term effects of vaccine introduction. In its simplicity, the model has shown that when vaccination is introduced, large transient spikes in disease cases may occur. These spikes are expected within at least 15 years from the start of vaccination with both intermediate efficacy and coverage. Despite the capability of vaccinations to decrease cumulative infections in the long term, the authors emphasize that the probable occurrence of large spikes should be considered when designing health policies. Indeed, those results were published well before any vaccine trial data were publicly available. An age-structured model was developed by Aguiar et al. [57], validated and parametrized with the available vaccine trial data [40], and has shown that a significant reduction of hospitalizations would only be possible when this vaccine is given to individuals with history of a previous dengue infection (seropositive individuals). However, a significant increase of hospitalizations was predicted, if this vaccine is administrated without a previous population screening, including vaccination of seronegative individuals.
In a more recent study, Kabir et al. [55] proposed a model for studying the effect of ADE for two vaccination types, the so-called primary and secondary vaccination standing for individuals who are seronegative and seropositive prior to vaccination, respectively. Applying the vaccination game approach, the authors have investigated the relationship between ADE and cost-efficiency of voluntary vaccination. As expected, model results have shown that if vaccines are effectively protecting seronegatives, vaccination of seropositives is not needed. Nevertheless, up to now, the only licensed dengue vaccine should not be administered to seronegative individuals, and therefore, results from this study are not compatible with the reality.
4.2. Vector-host transmission
To answer questions regarding the vector-host-pathogen interactions and disease control strategies, such as vector control and vaccination, more variables and assumptions, based on the available empirical data, are needed to be included into the model framework.
Hu et al. [89] have compared three models varying in complexity, a host-to-host model (without vector dynamics), a vector-host model (with latency class for vectors only, i.e., an extra model compartment where the mosquitoes are infected but not infectious, and hence unable to transmit the disease during the period of latency time), and the vector-host model (with latency compartments for both, vector and host dynamics). The authors have shown that the introduction of vector dynamics explicitly stabilizes the complex dynamics found in the host-to-host framework. As the assumption of cross-protection alone was not enough to explain the complexity of the data, the ADE effect increasing disease transmission of secondary infections, as opposed to the results presented in [60], [63], [68], was needed to describe the epidemiological data.
Integration of vector dynamics within host-to-host models is straightforward, with a simple Susceptible-Infected (SI) type model, as proposed in [71] and presented in Fig. 5 .
Fig. 5.
Schematic flow diagram for vector compartments. With vector population size M = U + Vi + Vj, susceptible vector population (U) and infected vector population carrying i,j dengue strain (Vi, Vj), with i,j = 1,2,3,4 and i ≠ j. For host population size N, the infection rate is parametrized by β, and ϕ is a scaling factor used to differentiate the infectivity ϕβ of secondary infections with respect to the baseline infectivity β of primary infection.
For the multi-strain vector-host minimalistic transmission model, assuming two dengue serotypes and only two possible infections, as proposed by Rashkov et al. [71], the complete ODE system can be written as shown in Equation System (2).
| (2) |
This is a host-vector model for dengue with two strains, TCI for the hosts, and possible secondary infections. The authors investigated the existence of endemic equilibria in one-strain and two-strain models, performed bifurcation analysis, and compared the results to the host-to-host two-strain model described in [68]. Similarly to the observations described in [89], results have shown that the explicit inclusion of vector dynamics into the host-to-host models significantly reduces the complexity of the system. However, by introducing yearly seasonal forcing in mosquito biting by means of a sinusoidal time variation of the number of mosquitoes, complex dynamics is also observed (for the same range of parameter values where complex dynamics occurs in [68]), see [71, Fig. 16].
Murillo et al. [88] presented a two-genotype-strain model using vertical transmission, in which the competitive dynamics between dengue virus genotypes is introduced in the vector-host dengue model. In the presence of vertical transmission, results showed that even a low probability of vertical transmission can have a major impact on the long-term dynamics of dengue fever. This determines the difference between failed outbreaks or invasions, as well as the possibility for the disease to become endemic in a population. Later, Anggriani et al. [75] have developed and analyzed a multi-serotype model with possible reinfection with homologous dengue serotype. A sensitivity analysis was performed showing that the reinfection parameter significantly influences the dynamics of primary and secondary infections. The biological assumption of hosts experiencing a more infectious secondary infection with a homologous dengue serotype is debatable, see [16], [122] and [123].
Lourenço et al. [90], [92] used a multi-strain vector-host model that includes an explicit mosquito vector component, TCI after primary infection, and seasonal forcing in mosquito biting. In [92], stochastic simulations were performed to explore the invasion dynamics of a novel dengue genotype in an endemic population with four co-circulating serotypes. The determinants for fixation success and rate, as well as their epidemiological consequences, were evaluated. While viral fitness is linked to invasion success and competitive exclusion of the resident genotype, the authors demonstrated that the epidemiological environment is more important for successful serotype emergence. In [90], the authors explored spatial and non-spatial multi-strain dengue models. They showed that even in the absence of immunological rivalry, spatially explicit multi-strain systems can display all of the specified epidemiological dynamics.
Another complex model was proposed by Coudeville and Garnett [91]. An age-structured, vector-host and serotype-specific compartmental model, including seasonality, was developed and analyzed. The authors have shown that short-term cross-protection (between 6-17 months) is critical to replicating real-world data. The assumption of individuals being able to be sequentially infected by all four serotypes, instead of only two, performed well in terms of data fitting. Results suggest that vaccination can decrease the frequency and magnitude of outbreaks, and alter the age distribution of disease cases. By adding vaccine dynamics to their model, they show that the overall impact of vaccination depends on the efficacy and the duration of protection that the vaccine confers.
Similar to the model proposed in [91], Knerer and colleagues [85] have developed a model featuring seasonality, age-structure, and consecutive infection by all four serotypes of dengue. The model was able to describe the national data from Thailand when incorporating seasonality and TCI between serotypes. The impact of combined vector-control and vaccination strategies on disease transmission was evaluated and although combining vaccination with other control strategies was shown to be more effective, their results have shown that a vaccine with low efficacy would have a positive impact on dengue transmission. Using the same model, the authors examine the cost-effectiveness of well known measures against dengue and its combinations [74]. The impact and cost-effectiveness of Wolbachia as a vector control strategy deployed at scale on a nationwide basis was evaluated through an exploratory analysis.
The effects of Wolbachia on dengue transmission dynamics were also evaluated by Ndii et al. [82], [86]. The authors developed a vector-host mathematical model in the presence of two dengue serotypes, suggesting that the presence of Wolbachia significantly reduces the transmission of dengue [82] and will be beneficial in the presence of multiple dengue serotypes [86].
A two-serotype vector-host model with ADE, cross-protection, and seasonality was proposed by Knipl and Moghadas [87]. Based on estimates of vaccine efficacy from [38], [39], their results have shown that disease eradication was not feasible. While higher vaccination coverage leads to lower numbers of infections, severe cases would increase due to ADE or waning immunity.
Maier at al. [80] have developed a model including ADE to examine the optimal vaccination age against dengue in Brazil. Using epidemiological data from Brazil, the authors have estimated the basic reproduction number and the optimal vaccination age for each of the four dengue serotypes, showing that the optimal vaccination age varies depending on the serotypes in circulation. A mathematical model with two virus strains, vector mosquito population and TCI was proposed by González Morale et al. [81] to investigate the effects of various vaccination strategies based on vaccine efficacy values, transmission intensity, and cross-immunity period. Results have shown that the period of cross-immunity plays a crucial role for disease incidence reduction and overall disease transmission dynamics.
Hendron and Bonsall [84] developed an epidemiological model for dengue virus transmission between vector and hosts to explore the combined effects of vector control using genetic variants of the sterile insect technique (SIT) and vaccination in small networks. The authors demonstrated that while mixed strategy solutions are more effective, the use of imperfect control strategies may be counterproductive, with host migration throughout this limited network increasing the severity of epidemics.
A model to examine the fundamental roles of demographic and spatial structures in epidemic initiation, growth and control is proposed by Falcón-Lezama [83]. By dividing the human population into patches according to the mobility and adding epidemic submodels for host and vector populations, authors focus on the role of highly mobile groups to show that the key factors promoting disease spreading are local dilution and spatial connectivity, characterized by the vector–host ratio and by the extent of habitually variable movement patterns, respectively.
Using two different models, Mishra and Gakkhar [73], [79] have examined the vector-host dynamics of dengue. In [79], a vector-host model considering two patches with different dengue serotypes in each patch is developed to evaluate the effect of human migration on the prevalence of dengue. The authors have concluded that emigration from a patch decreases the basic reproduction number for that patch while immigration has the opposite effect. A vector-host model for two dengue serotypes incorporating ADE was analyzed in [73], suggesting that a higher ADE factor allows for the second serotype to further persist.
Champagne and Cazelles [78] have compared deterministic and stochastic modeling frameworks for the dengue transmission disease. Five compartmental models, increasing in complexity by incorporating vector-borne transmission, explicit asymptomatic infections and interacting virus serotypes, are compared as they were able to reproduce dengue data from rural Cambodia. Results have shown that although the deterministic models provide a good approximation of the mean trajectory for a low computational cost, the stochastic frameworks better reflect and account for parameter and simulation uncertainty.
A significant amount of research on vector-host dynamics of dengue has also focused on optimizing interventions to mitigate the disease [70], [72], [76], [77]. Optimal control aims to identify solutions of optimization problems in dynamical systems with the aim of minimizing outcomes (e.g. infections, deaths) and the cost of implementing the interventions/controls [124]. Three controls generally appear in the vector-host dengue literature—precautionary measures (), vector control (), and more recently, vaccination (). Precautionary measures are controls that inhibit contact and/or transmission between a susceptible host and an infected vector. These typically include encouraging the use of mosquito nets and public awareness campaigns. Vector controls include the use of larvicides and fumigation to directly reduce the population size of vectors. Finally, vaccination measures decrease the number of susceptible hosts.
These controls are time-varying functions that may take values between 0 to 1, with 0 representing no usage of the controls and 1 representing full implementation of the control at time t. One can incorporate these controls in our generic vector-host model as additional parameters. Precautionary measures may be represented by the factor multiplied to the transmission term between the susceptible hosts and infected vectors. Vector-control may be represented by adding in the death rate for mosquitoes. Finally, the vaccination control may be incorporated by adding a removal term in the susceptible host population represented by .
A generic optimal control problem in a vector-host dengue model can be summarized as follows. One searches to minimize a cost function
| (3) |
which is optimized under the constraints of the dynamical vector-host model by using Lagrange multipliers . The solution for the optimal control problem can be obtained by applying Pontryagin's Minimum Principle [124], [125], that derives the necessary conditions to find the optimal solutions as follows: if is an optimal solution of an optimal control problem, then there exists a non-trivial vector function satisfying the following equalities
Numerical solutions can be obtained through a Forward-Backward Sweep Method (FBSM). We refer the reader to [124] for further details on this algorithm. Ultimately, the resulting solutions are values of the control function varying with time t that would minimize both the number of infections and cost of the controls. This is a tool that may aid health policymakers in designing key policies that both mitigate disease spread while avoiding unnecessary economic losses.
Bock and Jayathunga [76] developed a multi-patch vector-host model for dengue incorporating mosquitoes infected with the Wolbachia bacterium as control measure, either by reducing the level of virus in the mosquitoes or by shortening the vectors' life span. Numerical results show that Wolbachia vectors reduces the vector population, thus reducing disease spreading. A mathematical vector-host model of dengue transmission and vaccination was developed by Shim [77]. The model considers the effect of ADE and different immunological profiles for the human host. The optimal control problem for the dengue vaccination model is formulated to minimize the cost associated with dengue infection as well as vaccination for a finite time.
Ghosh et al. [72] have presented a qualitative analysis and optimal control for a multi-strain dengue model allowing co-infections. Three control strategies to reduce the infection in human and mosquito population, namely awareness efforts to protect human from mosquito bites, treatment efforts for infected human and mosquitoes killing efforts. The model was analyzed first by considering all the control efforts constant, and then, by considering that all that the controls are time dependent. Using Pontryagin's maximum principle, results were compared. Positive impact for implementing three controls to reduce infections was demonstrated, with awareness efforts to protect humans from mosquitoes bites along with treatment been more effective than the mosquitoes killing efforts along with treatment.
More recently, Xue and colleagues [70] have developed a two-infection multi-strain vector-host dengue model, including a latent (exposure) class for the host and for vectors. Via a sensitivity analysis, the authors have identified the important factors that impact the transmission dynamics of dengue virus. Although the models consider TCI, this parameter was not explored. Incorporation of two control variables representing i) improving the awareness of humans and ii) enhancing mosquito control to mitigate disease transmission, were evaluated under optimal control aspect by applying the Pontryagin's Maximum Principle, taking into account the corresponding economic costs.
4.3. Within-host transmission
Within-host models considering the dynamic interaction between free virus and susceptible target cells have been proposed, see e.g. [109], [110], [126], [127], with models differing on the functional form to model viral infectivity, immune response, and viral clearance dynamics.
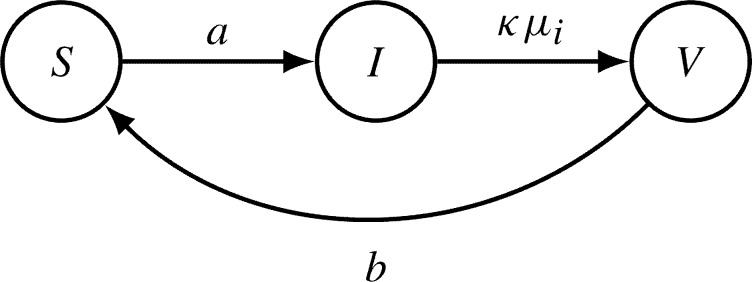
At microscopic level, within-host models are able to explore the dynamics of viral load and antibodies responses during dengue infections. Although the role of pre-existing dengue serotype specific antibodies in a secondary dengue infection with an explicit mechanism to explain its protective or enhancing effect has not been deeply explored yet, this approach becomes essential to understand the role of TCI and ADE, and to evaluate the impact of vaccination. The first step to develop a within-host model is the formulation of a simple SIV model to describe viral replication dynamics during the initial infection process. The state-flow diagram is shown in Fig. 6 , where S denotes the susceptible target cells, I denotes the infected cells and V stands for free viral particles that are produced and released during the dengue infection process.
Fig. 6.
State-flow diagram of a minimal within-host SIV model. With susceptible target cells S, infected cells I and viral particles V, the transitions from one to another state are parametrized by a, the infection rate of susceptible target cells, κμi, the viral replication with disease induced mortality rate μi of infected cells, and b the removal rate of viral particles during the infection process of a susceptible target cell.
The process of viral replication during a primary infection without immunological response, as recently proposed by Sebayang et al. [22], is given by
| (4) |
where and are, respectively, the production and mortality rate of susceptible target cells. While a is the infection rate, the mortality rate of infected cell, κ is the viral replication factor, and b is the removal rate of viral particles during the infection process of susceptible cells. We noted that since more than one viral particle is needed to generate one infected cell.
A target cell limited model was proposed by Ben-Shachar and Koelle [109]. With a model framework including a class of natural killer cells N and interferon F, a group of signaling proteins produced and released by host cells in response to the presence of several viruses [128], the authors have investigated three models with increasing complexity. Focused on determining the critical components of the innate and the adaptive immune responses able to reproduce features of dengue infections, the authors suggested that the innate immune response alone would be enough to capture the characteristic features of a primary symptomatic dengue infection, while a higher infectivity rate (mimicking ADE) and infected cell clearance by T cells are additionally needed to describe the characteristic features observed for a secondary dengue infection. The same authors have proposed a model to understand the individual viral load dynamics and the clinical manifestation of dengue infections [107]. By fitting the models with empirical data, they have shown that cellular immune response plays an important role in regulating viral load during a secondary dengue infection, providing statistical support for ADE and disease severity. Later, the authors have studied the transmission-clearance trade-offs virulence evolution. Using viremia measurements data from symptomatic dengue-infected patients, it was shown that high viral loads come at the cost of accelerated viral clearance in both primary and secondary dengue infections. Moreover, the role of epidemiological context in shaping dengue virulence evolution was investigated, with optimal virulence, defined as disease severity, depending on the epidemiological setting of one or two dengue serotypes circulation.
Clapham et al. [106], [110] have developed mathematical models similar to the model proposed by Nuraini et al. [126], including four state variables and the adaptive immune response for infection clearance. The model described in [110] was parametrized by fitting data of plasma viral titers of primary and secondary infections with DENV-1 serotype in Vietnam. Different parameter sets were needed to describe primary and secondary cases, with infection rate enhancement resembling the well known ADE effect in heterologous secondary dengue infections. Moreover, the authors have investigated the effect of Chloroquine treatment on viral dynamics, a medication primarily used to prevent and treat malaria but that has biochemical properties that might be applied against some viral infections [129]. Results have shown that the therapy is only effective if started before the symptoms manifestation. Further modeling refinements were investigated by Clapham and colleagues in [106]. The authors have developed a multi-serotype modeling framework that was parametrized using data for antibody titres and viral load measurements recorded sequentially during infection from 53 Vietnamese dengue patients. Results have shown that the antibody kinetics are playing a critical part in controlling viral replication, giving insights into the role of different mechanisms for infection clearance.
The model described in [106] was further used by ten Bosch et al. [101], coupled with human demographic projections, to quantify the net infectiousness of individuals across the spectrum of dengue infection severity and to estimate the fraction of transmission attributable to people with symptomatic disease.
Thibodeaux and colleagues [95], [105] have analyzed the within-host model described in [106], [110] by considering a non-constant monocyte production rate. As theoretical papers, stability analysis was performed and the net reproductive rate of the virus was obtained. Sensitivity analysis to investigate different treatment strategies was performed. While antiviral medicines to decrease the viral replication in infected monocytes are observed to be beneficial, immunostimulatory medicines to remove infected monocytes shows an even better results. Another theoretical exercise is performed by Gulbudk and Browne [96]. The authors have proposed a multi-scale modeling approach to couple the immunological and epidemiological dengue dynamics. The multi-serotype model includes TCI and ADE. Stability analysis with the basic and the invasion reproduction numbers as a function of immunological variables was performed. Borisov and Dimitriu [98] developed a model including mature and immature dengue viruses, motivated by data presented in [130]. Stability analysis was performed and the basic reproduction number, as a function of infected cells producing noninfectious virions was computed.
Using the method of population of models (POMs), Mapder et al. [99] have explored the intrinsic variability of viremia of dengue-infected patients. To predict efficient intervention to control measures for dengue, the authors have used a population of bang-bang switches of defective interfering virus which is, in its simplicity, a spontaneously generated virus mutant from which a critical portion of the virus genome has been deleted [131]. A multi-scale immuno-epidemiological model of dengue infection is proposed by Nikin-Beers et al. [100]. The within-host virus dynamics is coupled to a population-level model through a system of partial differential equations to investigate the roles of order and type of infection in driving the long-term persistence of co-circulating dengue serotypes in a population.
A non-linear model for dengue primary infection incorporating the role of T immune cells as well as antibodies in the dynamics is proposed in [104], where a time delay during the process of antibodies secretion is considered. This model has been further extended in [93] by adding the response of the innate immune response through a class of interferons.
A more complex model including several other immunological classes, was proposed by Perera and Perera [102]. The authors have developed a computer simulation mathematical model, including both innate and adaptive immune responses, to understand the viral kinetics during dengue infection. Sensitivity analysis was carried out to identify key parameters describing disease dynamics related to different clinical manifestations. More recently, to explore the features of viral replication, antibody production and infection clearance over time, a model framework developed to describe qualitatively the dengue immunological response mediated by antibodies was recently proposed by Sebayang et al. [22]. The model complexity increases gradually by including an extra target cell, macrophages, that differentiate into an antigen presenting cell, triggering the antibodies production. Complexes virus-antibodies are generated to clear the infection. The ADE effect is lead by primary infection pre-existing antibodies which are activated by the presence of a new viral particle.
Nikin-Beers and Ciupe [108] developed a model considering both primary and secondary infections to determine the role of cross-reactive antibodies on severe disease clinical manifestations. The model was fitted with published data on viral load levels of patients who had confirmed a secondary dengue infection [132]. Results have shown that while a secondary infection with a homologous serotype is cleared immediately, infections with a heterologous serotype generate a higher viral load, which has been shown to be correlated with disease severity [32]. More recently, Camargo et al. [94] have investigated a model for a secondary heterologous infection, focusing on the role of antibody neutralization and enhancement. The authors have shown that while neutralizing antibodies generated after the secondary infection plays a major role in protection from the virus, the infection-enhancing activity of pre-existing antibodies is an important mechanism involved in disease severity due to the higher occurrence of dengue hemorrhagic fever and dengue shock syndrome (DHF/DSS) promoted by the ADE phenomenon.
Models to investigate simultaneous infection of a host by multiple pathogen species are often proposed. As an example, dengue and Zika viruses, closely related viruses, transmitted by the same vector and causing similar clinical symptoms. Those viruses are often co-circulating in regions where conditions for disease transmission are present. Given the phylogenetic proximity of dengue viruses to Zika virus, Tang et al. [97] have developed a model to investigate antibody-dependent enhancement on disease severity of Zika virus and dengue virus sequential and co-infections. Through numerical simulations, authors show that ADE is the key factor determining a sharp increase/decrease of viral load near the peak time in any secondary infection. While a prior dengue virus infection would increase the severity or protect the human host during a Zika virus infection is still an open question, a clearer understanding on the sequence of those infections are of major importance for endemic countries.
4.4. Dengue and COVID-19 co-infection modeling
Numerous articles published in the last two years ([133], [134], [135], [136], [137], [138], [139], [140], [141], [142], [143], [144], [145], [146], [147] to name a few) alert of the profound medical concern of the COVID-19 and dengue co-epidemic or syndemic (terms commonly used to refer to the conjunction of the COVID-19 pandemic and dengue in dengue-endemic regions, such as South America, Africa and the Southeast and South Asia). Both viruses present common clinical symptoms (cough, muscle aches, fatigue, skin rash, and petechiae), long incubation periods, serological cross-reactivity and pathophysiological similarities (such as capillary leakage, thrombocytopenia, and coagulopathy), which hinder their timely diagnosis [148], [149]. Indeed, there are even confirmed case reports of patients infected with both viruses (e.g., [150], [151], [152], [153], [154], [155], [156], [157]), but there are also cases in which early or incomplete tests may lead to misdiagnosis (a situation that is more prone to occur in regions with limited medical resources), as in the case reports [138], [158] where false-positive were obtained from serological testing for dengue in a (subsequently confirmed) COVID-19 infected patients. And the overlapping of both diseases not only worsens the condition of patients who are doubly infected or misdiagnosed, but it aggravates the overall burden on healthcare systems (with its terrible economic and socio-political consequences). However, almost none of the mathematical models used to describe these diseases in epidemiological terms so far consider their association, including those currently used to assist the decision-making on public health policies.
Omame and collaborators [159] are the first (and the only ones to our knowledge) to implement a deterministic compartmental model for the co-interaction of COVID-19 and dengue transmission dynamics, whose parameters were estimated after fitting with the cumulative confirmed daily COVID-19 cases and deaths (from Feb. 1, 2021 to Sep. 20, 2021) in Brazil (a highly dengue-endemic country). In essence, this model leaves aside the impact of multiple COVID-19 strains and seasonality or wave effects of the two diseases, and assumes that: individuals have equal probability of contact with each other, COVID-19 infected individuals are susceptible to dengue and vice versa, co-infected individuals can transmit either COVID-19 or dengue at the same time or can recover from only one disease at the same time, and the rate of transmissibility for singly infected and co-infected individuals is the same. They also extend the model by including optimal control strategies and their cost-effectiveness analyses. Despite the apparent simplicity of the model, their results indicate that dengue only or COVID-19 only control strategy substantially diminishes new co-infection cases; being the strategy that implements control against incident COVID-19 infection the most effective in preventing the number of co-infection cases, and the strategy implementing control against incident dengue infection the most cost-effective in controlling dengue and COVID-19 co-infections. However, as the same authors fairly acknowledge, there are difficulties in estimating the parameters, in particular, those that explain the susceptibility of dengue-infected individuals to COVID-19 and the susceptibility of COVID-19-infected individuals to dengue.
Another approach that has proven fruitful in capturing intrinsic properties of modeling infectious diseases is the generalization to fractional-order derivative of basic models. In particular, Rehman and collaborators [160] proposed a model for COVID-19 and dengue co-infection. They explored the effects of using different fractional order values (which, although the order is not a biological parameter, serves to describe the dynamic) for different fractional-derivatives (in the Caputo, Caputo–Fabrizio and Atangana–Baleanu sense) and pointed out that Caputo operator shows still better results in terms of stability. In a similar manner, this kind of modeling framework has been applied to study the co-dynamics of COVID-19 with malaria [161] and with tuberculosis [162]. Also, there exist studies where each disease has been analyzed independently: for instance, Hamdan and Kilicman [163] employed a fractional-order SIR-based model for dengue, while Owusu-Mensah et al. [164] developed a fractional-order SEIR based model for COVID-19.
From a different viewpoint, Aguiar et al. [165] explored the parallelism between some compartmental models commonly used to dengue and COVID-19, and elaborated a fully parametrized model for COVID-19, but without integrating dengue into the description, as mentioned in the previous section. It is worth noting that even if any of the models developed to describe dengue or COVID-19 (such as SIR or SHAR) could be extended to include the concomitance, the values of its fitting parameters might vary after the model's generalization.
A further possibility is explored by Cavany et al. [166] by using an agent-based model to determine how dengue incidences differ under a lockdown scenario. The model simulates the dengue transmission coupled to a realistic model of human movement (based on the city of Iquitos, in the Peruvian Amazon) and average distribution of mobile mosquito agents (following spatio-temporal estimates of abundance based on household surveys). Their findings qualitatively reproduce the observed behavior [147], [167], [168]: COVID-19 lockdown measures taken against COVID-19 may adversely alter the epidemiology of dengue. In the same vein, Jindal and Rao [169] extend the analysis of the impact of different lockdowns strategies on outbreaks of mosquito-borne diseases.
The presented approaches serve as a guide and open the door to future developments seeking to address the mutually dependent case of a pandemic disease with another endemic disease. As with the Omame et al. model [159], the parameter fitting problem due to missing data still hindrance in all these models, but as more data become available, the predictive models can be improved and cross-checked.
5. Discussion and conclusions
This paper is an extensive review of a variety of mathematical models used to describe dengue fever epidemiology, including the within host approach which is restricted to a small number of studies so far. With many open questions, modeling dengue dynamics is still a challenging task, and this review is of great utility to guide future mathematical research on the dengue fever epidemiology.
In the present work, multi-strain deterministic, stochastic and spatial modeling frameworks to describe dengue epidemiology were reviewed. Research papers describing the immunological dynamics during dengue infection were also included, counting 15 for the host-to-host, 23 for vector-host and 18 for within-host structural approaches. Our review of mathematical models for dengue fever epidemiology is timely, dealing with mathematical models applied to infectious diseases of major public health importance.
The restrictive keywords searching up to the selection and exclusion criteria have limited the number of papers studied for this review. We are aware that we might not citing all the important publications on dengue modeling published during the past 10 years, and we apologize in advance for any references missing. For earlier studies, we also refer to the references in articles cited here.
Addressing the limited understanding of epidemiological and immunological factors influencing the transmission dynamics of dengue, our study provides insights on general features to be considered to model aspects of real-world public health problems, such as the current pandemic scenario we are living in. Focused on future research directions of modeling new pathogens able to cause explosive outbreaks, considerations of new COVID-19 variants and the current vaccination programs using imperfect vaccines are discussed on the basis of recent experiences in dengue vaccine modeling.
5.1. Components of dengue models
The development of mathematical models involves formulation, analysis, interpretation and validation. After deciding on the system to be modeled, the basic framework is developed according to the underlying assumptions of the system, with mathematical equations governing the system in respect to the used parameter values that are often estimated by empirical data.
Different types of modeling approaches are used to model infectious disease dynamics. The approach is defined based on the specific problem to be described and understood. Although most of dengue models are deterministic, often formulated in terms of a system of differential equations to describe disease transmission in a population, some of them include stochastic features, which are essential to describe real world epidemics. Spatial models aim to understand the role of mobility (both of hosts and vectors) on disease spreading by including spatial interactions, either on individual levels or in metapopulation settings. The modeling approach for each of the mathematical models included in this review is shown in Table 1.
As for the host-to-host modeling framework, besides the transmission rate and recovery rate, the ADE effect, often described as the contribution of secondary infection to the overall force of infection, and the TCI, which refers to the temporal window of immune protection against secondary infection by any serotype, are common features used to describe dengue fever epidemiology. Life-long immunity to a specific serotype causing the infection is a common assumption. While TCI is only recently included in modeling, formulations of the ADE effect vary, with the parameter acting, most of the time, to enhance susceptibility or transmissibility. The combination of both are, however, important to understand the immunopathogenesis of severe disease. Seasonality is often used to mimic the effect of vector dynamics in simple host-to-host models. Nevertheless, many studies including explicitly the dynamics of mosquitoes, coupled with a host model, introduce seasonal forcing in the vector population dynamics. Then additional parameters such as incubation period, biting rate and the vector life span are considered. Those parameters are, however, difficult to be estimated due to the lack of good data and their wide ranges and different conditions in laboratory and nature.
Other features for dengue modeling are, for example, disease co-infection (either different pathogens or eventually different variants of the same microorganism), and control measures such as vector control and vaccination that are also modeled as combined strategies and used for optimal control evaluation.
Regarding within-host modeling, parameters are used at microscopic scales, dealing with concentration levels obtained by blood samples. The time scale is much faster than the ones used at macroscopic level (in months or years) and it is often evaluated per hour or day. Within-host parameters refer to laboratory data on viral load and antibody concentration, and on the immunological characteristics of human cells production, viral replication and infection clearance, for example.
The main components of the dengue models studied in this review are shown in the tables below. Definitions and ranges of the main parameters for host-to-host and vector-host transmission models are shown in Table 2, Table 3 , respectively. Table 4 shows the main parameters used for within-host models, describing the immunological responses of dengue infections. For the sake of simplicity, the parameter representation is not shown in the tables since the studies often use different notations for the same definitions.
Table 2.
List of parameters used in host-to-host modeling.
| Parameter definition | Range of values | References |
|---|---|---|
| Birth and death rate (year−1) | [] | [56], [57], [58], [59], [60], [62], [63], [64], [65], [67], [68], [69] |
| Recovery rate (year−1) | [26, 100] | [55], [56], [57], [58], [59], [60], [62], [63], [64], [65], [66], [67], [68], [69] |
| Transmission rate | [70, 400] | [55], [56], [57], [58], [60], [62], [63], [64], [65], [66], [67], [68], [69] |
| Temporary cross-protection period (year−1) | [1.8, 50] | [56], [57], [58], [60], [63], [64], [65], [67], [68] |
| Secondary infection contribution to force of infection | [0, 4] | [55], [56], [57], [58], [59], [60], [62], [63], [64], [67], [68], [69] |
| Enhancement of susceptibility | [1, ∞] | [58] |
| Enhancement of transmissibility | [1, 1.4] | [65] |
| Amplitude of seasonality | [0, 0.35] | [58], [61], [62], [63], [68], [119] |
| Degree of cross-protection | [0, 1] | [61], [89] |
| Vaccination coverage | [0, 1] | [57], [59] |
| Vaccine efficacy⁎ | [negative, 1] | [55], [57], [59], [62] |
Table 3.
List of parameters used in vector-host modeling.
| Parameter definition | Range of values | References |
|---|---|---|
| Birth and death rate for hosts (year−1) | [] | [61], [70], [71], [72], [74], [75], [78], [81], [84], [85], [88], [89] |
| Birth and death rate for vectors (day−1) | [] | [61], [70], [71], [72], [73], [74], [75], [78], [79], [81], [84], [85], [87], [88] |
| Recovery rate for hosts (day−1) | [] | [61], [70], [71], [72], [73], [74], [75], [76], [78], [79], [80], [81], [82], [83], [85], [86], [87], [88], [89], [91] |
| Transmission rate from vector to host (day−1) | [0, 0.5] | [61], [70], [72], [73], [74], [75], [76], [78], [79], [80], [81], [82], [84], [85], [86], [88], [90], [92] |
| Transmission rate from host to vector (day−1) | [0, 0.75] | [61], [70], [72], [73], [75], [76], [78], [79], [80], [81], [82], [84], [86], [88], [90], [91], [92] |
| Vector biting rate (day−1) | [0.26, 0.67] | [73], [80], [82], [83], [84], [86], [90], [91], [92] |
| Enhancement of susceptibility after primary infection | [1, 3.95] | [75], [91] |
| Reduction of susceptibility after primary infection | [0, 1] | [87] |
| Enhancement of transmissibility | [1, ∞] | [61], [74], [85], [87], [89], [91] |
| Immunity for same strain | [0, 0.5] | [75] |
| Incubation rate for hosts (day−1) | [0, 1] | [70], [74], [76], [78], [80], [81], [82], [83], [85], [86], [87], [90], [91], [92] |
| Incubation rate for vectors (day−1) | [0, 1] | [70], [74], [76], [78], [80], [82], [83], [85], [87], [91] |
| Disease-induced mortality for hosts (day−1) | [0, 10−3] | [70], [72], [73], [74], [79], [85] |
| Degree of cross-protection | [0, 1] | [61], [74], [85], [87], [89] |
| Temporary cross-protection period (day) | [2, 365 × 5] | [61], [71], [74], [81], [85], [87], [89], [90], [92] |
| Enhancement of disease severity after primary infection | [1, 2.8] | [91] |
| Vaccination coverage | [0, 0.95] | [74], [80], [81], [84], [85], [87], [91] |
| Vaccine efficacy | [0, 0.95] | [74], [80], [81], [84], [85], [91] |
| Vaccination protection period (year) | [1.8, 10] | [74], [80], [81], [84], [85], [91] |
| Enhanced transmissibility after waning of vaccination | 2 | [87] |
| Reduced susceptibility after vaccination | [0.25, 0.55] | [87] |
| Amplitude of seasonality | [0, 1] | [78], [82], [86], [90], [92] |
| Transmission rate from Wolbachia carrying mosquito to host | [0, 0.7] | [76], [82] |
| Transmission rate from host to Wolbachia-carrying mosquito | [0, 0.7] | [76], [82], [86] |
| Death rate of Wolbachia-carrying mosquito (day−1) | [0, 0.1] | [76], [82], [86] |
Table 4.
List of parameters used in within-host modeling.
| Parameter definition | Range of values | References |
|---|---|---|
| Initial value for target cells (cell ml−1) | [2 × 104,1 × 108] | [97], [98], [99], [103], [108], [109] |
| Initial value for free viral particles upon infection (cell ml−1) | [1, 357] | [22], [97], [132] |
| Initial number of infected cells (cell ml−1) | [0,3 × 10−4] | [101], [103], [108], [109] |
| Target cell production rate (cell ml−1 day−1) | [300,1.4 × 106] | [22], [97], [101], [102], [106], [107], [108], [110] |
| Death rate of susceptible target cells (day−1) | [0.03, 0.333] | [97], [101], [102], [105], [109], [110] |
| Infection rate of susceptible target cells (viral particle−1 day−1) | [5 × 10−11,1 × 10−8] | [22], [94], [98], [103], [106] |
| Death rate of infected target cells (day−1) | [0.14,3.5] | [22], [95], [102], [104], [105], [106], [108], [110] |
| Removal rate of infected cells per immune cell (day−1) | [0.001,0.05] | [95], [102], [105], [110] |
| Viral replication factor | [20, 10000] | [22], [98], [103], [105], [106], [108] |
| Virus clearance rate (day−1) | [0.03, 9.562] | [22], [93], [96], [98], [99], [102], [103], [105], [106], [108], [126] |
| Proportionality constant relating viral load to transmission rate | [0,0.03] | [100] |
| Antibody/Immune cells production rate (day−1) | [0.0265, 13.89] | [22], [94], [95], [98], [102], [105], [109] |
| Antibody decay rate (day−1) | [1/365, 0.07] | [102], [104], [105], [108], [170] |
| Incubation period (day) | 5.9 | [103] |
| Production rate of virions per infected cell (day−1) | [1 × 104,1.1 × 105] | [103], [110] |
| Recruitment rate of Natural Killer NK cells (day−1) | [0.52,0.0624] | [95], [109] |
| Killing rate of Natural Killer NK cells (day−1) | [5.74 × 10−4,2 × 10−3] | [98], [102], [103], [109] |
| Recruitment rate of T cells ((cell ml−1)−1 day−1) | [4.5 × 10−7,3 × 10−5] | [98], [103], [109] |
| Killing rate of T cells (day−1) | [1 × 10−6,1.2 × 10−4] | [98], [103], [109] |
| Killing rate of infected target cells by Natural Killer NK cells (day−1) | [0.002,0.077] | [98], [102] |
| Production rate of interferon INF (day−1) | 0.8 | [102] |
| Decay rate of interferon INF (day−1) | [0.7,1.6639] | [98], [102] |
| Cross-reactive antibody activation rate | 0.4 | [96] |
| Specific antibody activation rate | 0.5 | [96] |
| Fraction of infected cells producing immature virus | (0,0.9) | [98] |
5.2. Modeling dengue epidemiology in times of COVID-19
Mathematical models are storytellers. Built taking into account the epidemiological information about the disease, models are validated with real world data, giving insights into the disease spreading dynamics. They act as guiding tools to predict the future stages of epidemics, assisting public health authorities on decision making for disease control.
Since COVID-19 was declared as pandemic by the World Health Organization (WHO) [171], several modeling task forces were created to assist local public health managers and governments during the sanitary crisis. Able to describe the epidemic in terms of disease spreading and control, models developed within those task forces were able to give projections on the national health system and are still used to monitor the disease transmission during the application and lifting of control measures.
5.3. How dengue modeling experiences can help to understand the spread of COVID-19: features for a common modeling framework
Although dengue is a vector-borne disease, it is fair to say that disease epidemiology has similar features as observed for COVID-19. Both diseases are caused by pathogens with multiple variants (strains) and a significant proportion of the infected human hosts are asymptomatic or develop only mild symptoms, i.e., infected but still mobile. Disease severity and death occurs according to a hierarchy of risks [172], with age, pre-existing health conditions, and eventually serostatus prior to infection, enhancing (or eventually protecting) disease severity. Existing vaccines play a major role in controlling the spread of the disease and preventing severe symptoms manifestation when properly administrated.
As it is for dengue, the role of asymptomatic infections contributing to the spreading of COVID-19 has been of great concern. Motivated by dengue epidemiology and its large number of asymptomatic individuals, and the well known ADE effect enhancing disease severity during an infection with a heterologous serotype, Stollenwerk et al. [173] have proposed a SHAR (Susceptible-Hospitalized-Asymptomatic-Recovered) framework, an extension of the SIR epidemic model, to investigate the differences in transmission rates of symptomatic and asymptomatic infections. The model introduces a parameter ϕ to differentiate the infectivity ϕβ of mild/asymptomatic infections with respect to the baseline infectivity β of severe/hospitalized cases. The value of ϕ can be tuned to describe different situations. For dengue, a value of indicates that severe cases have larger infectivity (by assuming that individuals would have a higher viral load) than mild cases, while would indicate otherwise, describing the scenario in which asymptomatic individuals and mild cases contribute more to the spread of the infection, e.g., due to their higher mobility and the possibility of interaction as opposed to hospitalized individuals) than severe cases that are likely to be detected, hospitalized and therefore isolated.
While it is unlikely to observe ADE (via enhanced immune activation or via enhanced infection) in COVID-19 [174], [175], waning immunity and TCI are decisive for disease control. A detailed understanding on the immunological responses of recurrent infections with different variants, eventually co-infections with different pathogens, and vaccine effectiveness are needed to ensure the safety of medical interventions. Similarly, for COVID-19, the assumptions of ϕ being smaller or larger 1 can be justified as follows. While a value of indicates that severe cases have larger infectivity than mild cases (linked to enhanced coughing and sneezing), would be also used to describe the scenario in which asymptomatic individuals and mild cases contribute more to the spread of the infection (e.g., due to their higher mobility and the possibility of interaction) than severe cases (that are more likely to be detected and isolated). This model was refined to describe the epidemiology of COVID-19 [165]. The framework was later extended by including additional classes of Intensive Care Unit (ICU) admissions U, and deceased D, and for data analysis of cumulative disease data, also accounting the cumulative classes C, in the so-called SHARUCD framework [176], [177]. The analysis of the reproduction ratio and growth rates from the data [178] led to improved model versions. This framework is now being used to monitor disease transmission, while control measures were implemented and gradually lifted. To investigate the role of mild and asymptomatic infections on COVID-19 vaccines performance, the SHAR model was also used as a baseline framework, give insights on how to best combine the use of the available COVID-19 vaccines, optimizing the reduction of hospitalizations [179].
The inclusion of heterogeneity, spatial distancing and investigations on the role of imported cases during a controlling phase of an epidemic are examples of other (of many) aspects that are often investigated in different epidemiological contexts. It would not be different for COVID-19 modeling approaches [180], [181], [182]. Our previous modeling experiences and intuition have definitely made the efforts and challenges to develop a flexible modeling framework to guide decision making during the COVID-19 pandemic a bit easier.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This research is supported by the Basque Government through the “Mathematical Modeling Applied to Health” Project, BERC 2018-2021 program and by Spanish Ministry of Sciences, Innovation and Universities: BCAM Severo Ochoa accreditation SEV-2017-0718. M.A. has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 792494.
Communicated by Susan Li
References
- 1.Fischer D.B., Halstead S.B. Observations related to pathogenesis of dengue hemorrhagic fever. V. Examination of agspecific sequential infection rates using a mathematical model. Yale J Biol Med. 1970;42(5):329–349. https://pubmed.ncbi.nlm.nih.gov/5419207 [PMC free article] [PubMed] [Google Scholar]
- 2.Johansson M.A., Hombach J., Cummings D.A. Models of the impact of dengue vaccines: a review of current research and potential approaches. Vaccine. 2011;29(35):5860–5868. doi: 10.1016/j.vaccine.2011.06.042. https://www.sciencedirect.com/science/article/pii/S0264410X11009066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Andraud M., Hens N., Marais C., Beutels P. Dynamic epidemiological models for dengue transmission: a systematic review of structural approaches. PLoS ONE. 2012;7(11) doi: 10.1371/journal.pone.0049085. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0049085 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pan American Health Organization Aedes aegypti: biology and ecology. https://iris.paho.org/bitstream/handle/10665.2/28514/PNSP8664_eng.pdf?sequence=1&isAllowed=y Retrieved from.
- 5.World Health Organization Dengue and severe dengue - key facts. https://www.who.int/news-room/fact-sheets/detail/dengue-and-severe-dengue Retrieved from.
- 6.Brady O.J., Gething P.W., Bhatt S., Messina J.P., Brownstein J.S., Hoen A.G., et al. Refining the global spatial limits of dengue virus transmission by evidence-based consensus. PLoS Negl Trop Dis. 2012;6(8) doi: 10.1371/journal.pntd.0001760. https://journals.plos.org/plosntds/article?id=10.1371/journal.pntd.0001760 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tuiskunen Bäck A., Lundkvist Å. Dengue viruses – an overview. Infect Ecol Epidemiol. 2013;3(1) doi: 10.3402/iee.v3i0.19839. https://www.tandfonline.com/doi/full/10.3402/iee.v3i0.19839 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Westaway E., Brinton M., Gaidamovich Y., Horzinek M., Igarashi A., Kääriäinen L., et al. Intervirology. 1985;24(4):183–192. doi: 10.1159/000149642. https://www.karger.com/Article/FullText/149642 [DOI] [PubMed] [Google Scholar]
- 9.Wang E., Ni H., Xu R., Barrett A.D.T., Watowich S.J., Gubler D.J., et al. Evolutionary relationships of endemic/epidemic and sylvatic dengue viruses. J Virol. 2000;74(7):3227–3234. doi: 10.1128/jvi.74.7.3227-3234.2000. https://journals.asm.org/doi/10.1128/JVI.74.7.3227-3234.2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Guzman M.G., Gubler D.J., Izquierdo A., Martinez E., Halstead S.B. Dengue infection. Nat Rev Dis Primers. 2016;2(1) doi: 10.1038/nrdp.2016.55. http://www.nature.com/articles/nrdp201655 [DOI] [PubMed] [Google Scholar]
- 11.Bhatt S., Gething P.W., Brady O.J., Messina J.P., Farlow A.W., Moyes C.L., et al. The global distribution and burden of dengue. Nature. 2013;496(7446):504–507. doi: 10.1038/nature12060. http://www.nature.com/articles/nature12060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sangkawibha N., Rojanasuphot S., Ahandrik S., Viriyapongse S., Jatanasen S., Salitul V., et al. Risk factors in dengue shock syndrome: a prospective epidemiologic study in Rayong, Thailand. Am J Epidemiol. 1984;120(5):653–669. doi: 10.1093/oxfordjournals.aje.a113932. https://academic.oup.com/aje/article-abstract/120/5/653/90744?redirectedFrom=fulltext [DOI] [PubMed] [Google Scholar]
- 13.Guzmán M.G., Kouri G. Dengue: an update. Lancet Infect Dis 2. 2002;1:33–42. doi: 10.1016/s1473-3099(01)00171-2. https://www.thelancet.com/journals/laninf/article/PIIS1473-3099(01)00171-2/fulltext [DOI] [PubMed] [Google Scholar]
- 14.Sierra B., Perez A.B., Vogt K., Garcia G., Schmolke K., Aguirre E., et al. Secondary heterologous dengue infection risk: disequilibrium between immune regulation and inflammation? Cell Immunol. 2010;262(2):134–140. doi: 10.1016/j.cellimm.2010.02.005. https://www.sciencedirect.com/science/article/abs/pii/S0008874910000353 [DOI] [PubMed] [Google Scholar]
- 15.John A.L.St., Rathore A.P.S. Adaptive immune responses to primary and secondary dengue virus infections. Nat Rev Immunol. 2019;19(4):218–230. doi: 10.1038/s41577-019-0123-x. http://www.nature.com/articles/s41577-019-0123-x [DOI] [PubMed] [Google Scholar]
- 16.Weiskopf D., Sette A. T-cell immunity to infection with dengue virus in humans, frontiers in immunology 5. https://www.frontiersin.org/articles/10.3389/fimmu.2014.00093/full [DOI] [PMC free article] [PubMed]
- 17.Halstead S.B. Dengue hemorrhagic fever: two infections and antibody dependent enhancement, a brief history and personal memoir. Rev Cuba Med Trop. 2002;54:171–179. http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S0375-07602002000300002&nrm=iso [PubMed] [Google Scholar]
- 18.Halstead S.B. Advances in virus research. vol. 60. Academic Press; 2003. Neutralization and antibody-dependent enhancement of dengue viruses; pp. 421–467.https://www.sciencedirect.com/science/article/abs/pii/S0065352703600114 [DOI] [PubMed] [Google Scholar]
- 19.Rothman A.L. Dengue: defining protective versus pathologic immunity. J Clin Invest. 2004;113(7):946–951. doi: 10.1172/JCI21512. http://www.jci.org/articles/view/21512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Clapham H.E., Cummings D.A.T., Johansson M.A. Immune status alters the probability of apparent illness due to dengue virus infection: evidence from a pooled analysis across multiple cohort and cluster studies. PLoS Negl Trop Dis. 2017;11(9) doi: 10.1371/journal.pntd.0005926. https://journals.plos.org/plosntds/article?id=10.1371/journal.pntd.0005926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rothman A.L. Dengue virus. Springer; Berlin, Heidelberg: 2009. Cellular immunology of sequential dengue virus infection and its role in disease pathogenesis; pp. 83–98. [DOI] [PubMed] [Google Scholar]
- 22.Sebayang A.A., Fahlena H., Anam V., Knopoff D., Stollenwerk N., Aguiar M., et al. Modeling dengue immune responses mediated by antibodies: a qualitative study. Biology. 2021;10(9):941. doi: 10.3390/biology10090941. https://www.mdpi.com/2079-7737/10/9/941 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Guzman M.G., Halstead S.B., Artsob H., Buchy P., Farrar J., Gubler D.J., et al. Dengue: a continuing global threat. Nat Rev Microbiol. 2010;8(S12):S7–S16. doi: 10.1038/nrmicro2460. http://www.nature.com/articles/nrmicro2460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dejnirattisai W., Jumnainsong A., Onsirisakul N., Fitton P., Vasanawathana S., Limpitikul W., et al. Cross-reacting antibodies enhance dengue virus infection in humans. Science. 2010;328(5979):745–748. doi: 10.1126/science.1185181. https://www.science.org/doi/10.1126/science.1185181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Boonnak K., Dambach K.M., Donofrio G.C., Tassaneetrithep B., Marovich M.A. Cell type specificity and host genetic polymorphisms influence antibody-dependent enhancement of dengue virus infection. J Virol. 2011;85(4):1671–1683. doi: 10.1128/JVI.00220-10. https://journals.asm.org/doi/10.1128/JVI.00220-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bournazos S., Gupta A., Ravetch J.V. The role of IgG Fc receptors in antibody-dependent enhancement. Nat Rev Immunol. 2020;20(10):633–643. doi: 10.1038/s41577-020-00410-0. https://www.nature.com/articles/s41577-020-00410-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Guzman M.G., Harris E. Dengue. Lancet. 2015;385(9966):453–465. doi: 10.1016/S0140-6736(14)60572-9. https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(14)60572-9/fulltext [DOI] [PubMed] [Google Scholar]
- 28.Wang W.-K., Chao D.-Y., Kao C.-L., Wu H.-C., Liu Y.-C., Li C.-M., et al. High levels of plasma dengue viral load during defervescence in patients with dengue hemorrhagic fever: implications for pathogenesis. Virology. 2003;305(2):330–338. doi: 10.1006/viro.2002.1704. https://www.sciencedirect.com/science/article/pii/S0042682202917046 [DOI] [PubMed] [Google Scholar]
- 29.Guilarde A.O., Turchi M.D., Siqueira J.B., Jr., Feres V.C.R., Rocha B., Levi J.E., et al. Dengue and dengue hemorrhagic fever among adults: clinical outcomes related to viremia, serotypes, and antibody response. J Infect Dis. 2008;197(6):817–824. doi: 10.1086/528805. https://academic.oup.com/jid/article/197/6/817/919531 [DOI] [PubMed] [Google Scholar]
- 30.Halstead S.B., O'Rourke E.J. Antibody-enhanced dengue virus infection in primate leukocytes. Nature. 1977;265(5596):739–741. doi: 10.1038/265739a0. http://www.nature.com/articles/265739a0 [DOI] [PubMed] [Google Scholar]
- 31.Kliks S.C., Nisalak A., Brandt W.E., Wahl L., Burke D.S. Antibody-dependent enhancement of dengue virus growth in human monocytes as a risk factor for dengue hemorrhagic fever. Am J Trop Med Hyg. 1989;40(4):444–451. doi: 10.4269/ajtmh.1989.40.444. https://www.ajtmh.org/view/journals/tpmd/40/4/article-p444.xml [DOI] [PubMed] [Google Scholar]
- 32.Vaughn D.W., Green S., Kalayanarooj S., Innis B.L., Nimmannitya S., Suntayakorn S., et al. Dengue viremia titer, antibody response pattern, and virus serotype correlate with disease severity. J Infect Dis. 2000;181(1):2–9. doi: 10.1086/315215. https://academic.oup.com/jid/article/181/1/2/892842 [DOI] [PubMed] [Google Scholar]
- 33.Martial J., Dussart P., Plumelle Y., Moravie V., Verlaeten O., Najioullah F., et al. Influence of the dengue serotype, previous dengue infection, and plasma viral load on clinical presentation and outcome during a dengue-2 and dengue-4 co-epidemic. Am J Trop Med Hyg. 2008;78(6):990–998. https://www.ajtmh.org/view/journals/tpmd/78/6/article-p990.xml [PubMed] [Google Scholar]
- 34.Yamanaka A., Imad H.A., Phumratanaprapin W., Phadungsombat J., Konishi E., Shioda T. Antibody-dependent enhancement representing in vitro infective progeny virus titer correlates with the viremia level in dengue patients. Sci Rep. 2021;11(1) doi: 10.1038/s41598-021-91793-0. http://www.nature.com/articles/s41598-021-91793-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.World Health Organization Dengue vaccine research. 2017. https://www.who.int/immunization/research/development/dengue_vaccines/en/ Retrieved from. [DOI] [PubMed]
- 36.Wilder-Smith A. Dengue vaccine development by the year 2020: challenges and prospects. Curr Opin Virol. 2020;43:71–78. doi: 10.1016/j.coviro.2020.09.004. https://www.sciencedirect.com/science/article/pii/S1879625720300948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Deng S.-Q., Yang X., Wei Y., Chen J.-T., Wang X.-J., Peng H.-J. A review on dengue vaccine development. Vaccines. 2020;8(1):63. doi: 10.3390/vaccines8010063. https://www.mdpi.com/2076-393X/8/1/63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Capeding M.R., Tran N.H., Hadinegoro S.R.S., Ismail H.I.H.M., Chotpitayasunondh T., Chua M.N., et al. Clinical efficacy and safety of a novel tetravalent dengue vaccine in healthy children in Asia: a phase 3, randomised, observer-masked, placebo-controlled trial. Lancet. 2014;384(9951):1358–1365. doi: 10.1016/S0140-6736(14)61060-6. https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(14)61060-6/fulltext [DOI] [PubMed] [Google Scholar]
- 39.Villar L., Dayan G.H., Arredondo-García J.L., Rivera D.M., Cunha R., Deseda C., et al. Efficacy of a tetravalent dengue vaccine in children in Latin America. N Engl J Med. 2015;372(2):113–123. doi: 10.1056/NEJMoa1411037. http://www.nejm.org/doi/10.1056/NEJMoa1411037 [DOI] [PubMed] [Google Scholar]
- 40.Hadinegoro S.R., Arredondo-García J.L., Capeding M.R., Deseda C., Chotpitayasunondh T., Dietze R., et al. Efficacy and long-term safety of a dengue vaccine in regions of endemic disease. N Engl J Med. 2015;373(13):1195–1206. doi: 10.1056/NEJMoa1506223. http://www.nejm.org/doi/10.1056/NEJMoa1506223 [DOI] [PubMed] [Google Scholar]
- 41.Biswal S., Reynales H., Saez-Llorens X., Lopez P., Borja-Tabora C., Kosalaraksa P., et al. Efficacy of a tetravalent dengue vaccine in healthy children and adolescents. N Engl J Med. 2019;381(21):2009–2019. doi: 10.1056/NEJMoa1903869. http://www.nejm.org/doi/10.1056/NEJMoa1903869 [DOI] [PubMed] [Google Scholar]
- 42.Biswal S., Borja-Tabora C., Martinez Vargas L., Velásquez H., Theresa Alera M., Sierra V., et al. Efficacy of a tetravalent dengue vaccine in healthy children aged 4–16 years: a randomised, placebo-controlled, phase 3 trial. Lancet. 2020;395(10234):1423–1433. doi: 10.1016/S0140-6736(20)30414-1. https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(20)30414-1/fulltext [DOI] [PubMed] [Google Scholar]
- 43.Rivera L., Biswal S., Sáez-Llorens X., Reynales H., López-Medina E., Borja-Tabora C., et al. Three years efficacy and safety of Takeda's dengue vaccine candidate (TAK-003) Clin Infect Dis. 2021 doi: 10.1093/cid/ciab864. https://academic.oup.com/cid/advance-article/doi/10.1093/cid/ciab864/6381105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.World Health Organization Dengue vaccine: WHO position paper, July 2016 – recommendations. Vaccine. 2017;35(9):1200–1201. doi: 10.1016/j.vaccine.2016.10.070. https://www.sciencedirect.com/science/article/pii/S0264410X16310192 [DOI] [PubMed] [Google Scholar]
- 45.World Health Organization Strategic Advisory Group of Experts (SAGE) on Immunization Background paper on dengue vaccines prepared by the SAGE working group on dengue vaccines and the WHO secretariat. 2016. http://www.who.int/immunization/sage/meetings/2016/april/presentations background docs/en Retrieved from.
- 46.Aguiar M., Stollenwerk N., Halstead S.B. The risks behind Dengvaxia recommendation. Lancet Infect Dis. 2016;16(8):882–883. doi: 10.1016/S1473-3099(16)30168-2. https://www.thelancet.com/journals/laninf/article/PIIS1473-3099(16)30168-2/fulltext [DOI] [PubMed] [Google Scholar]
- 47.Halstead S.B. Critique of World Health Organization recommendation of a dengue vaccine. J Infect Dis. 2016;214(12):1793–1795. doi: 10.1093/infdis/jiw340. https://academic.oup.com/jid/article/214/12/1793/2632615 [DOI] [PubMed] [Google Scholar]
- 48.Aguiar M., Stollenwerk N. Dengvaxia efficacy dependency on serostatus: a closer look at more recent data. Clin Infect Dis. 2018;66(4):641–642. doi: 10.1093/cid/cix882. https://academic.oup.com/cid/article/66/4/641/4560630 [DOI] [PubMed] [Google Scholar]
- 49.Aguiar M., Stollenwerk N. Dengvaxia: age as surrogate for serostatus. Lancet Infect Dis. 2018;18(3):245. doi: 10.1016/S1473-3099(17)30752-1. https://linkinghub.elsevier.com/retrieve/pii/S1473309917307521 [DOI] [PubMed] [Google Scholar]
- 50.Halstead S.B., Katzelnick L.C., Russell P.K., Markoff L., Aguiar M., Dans L.R., et al. Ethics of a partially effective dengue vaccine: lessons from the Philippines. Vaccine. 2020;38(35):5572–5576. doi: 10.1016/j.vaccine.2020.06.079. https://www.sciencedirect.com/science/article/pii/S0264410X20308823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sridhar S., Luedtke A., Langevin E., Zhu M., Bonaparte M., Machabert T., et al. Effect of dengue serostatus on dengue vaccine safety and efficacy. N Engl J Med. 2018;379(4):327–340. doi: 10.1056/NEJMoa1800820. http://www.nejm.org/doi/10.1056/NEJMoa1800820 [DOI] [PubMed] [Google Scholar]
- 52.World Health Organization Revised SAGE recommendation on use of dengue vaccine. 2018. https://www.who.int/immunization/diseases/dengue/revised_SAGE_recommendations_dengue_vaccines_apr2018/en/ Retrieved from.
- 53.World Health Organization Weekly epidemiological record (7 September 2018), 93rd year, no 36, 457-476. Dengue vaccine: WHO position paper – September 2018. https://apps.who.int/iris/bitstream/handle/10665/274315/WER9336.pdf?ua=1 Retrieved from.
- 54.Aguiar M., Stollenwerk N. The impact of serotype cross-protection on vaccine trials: DENVax as a case study. Vaccines. 2020;8(4):674. doi: 10.3390/vaccines8040674. https://www.mdpi.com/2076-393X/8/4/674 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kabir K.A., Tanimoto J. Cost-efficiency analysis of voluntary vaccination against n-serovar diseases using antibody-dependent enhancement: a game approach. J Theor Biol. 2020;503 doi: 10.1016/j.jtbi.2020.110379. https://www.sciencedirect.com/science/article/pii/S0022519320302344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Aguiar M., Stollenwerk N. Mathematical models of dengue fever epidemiology: multi-strain dynamics, immunological aspects associated to disease severity and vaccines. Commun Biomath Sci. 2017;1(1):1. http://journals.itb.ac.id/index.php/cbms/article/view/5767 [Google Scholar]
- 57.Aguiar M., Stollenwerk N., Halstead S.B. The impact of the newly licensed dengue vaccine in endemic countries. PLoS Negl Trop Dis. 2016;10(12) doi: 10.1371/journal.pntd.0005179. https://journals.plos.org/plosntds/article?id=10.1371/journal.pntd.0005179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.ten Bosch Q.A., Singh B.K., Hassan M.R.A., Chadee D.D., Michael E. The role of serotype interactions and seasonality in dengue model selection and control: insights from a pattern matching approach. PLoS Negl Trop Dis. 2016;10(5) doi: 10.1371/journal.pntd.0004680. https://journals.plos.org/plosntds/article?id=10.1371/journal.pntd.0004680 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Pandey A., Medlock J. The introduction of dengue vaccine may temporarily cause large spikes in prevalence. Epidemiol Infect. 2015;143(6):1276–1286. doi: 10.1017/S0950268814001939. https://www.cambridge.org/core/journals/epidemiology-and-infection/article/introduction-of-dengue-vaccine-may-temporarily-cause-large-spikes-in-prevalence/238C2D2D712D3DBE68BB203B38F00FA6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kooi B.W., Aguiar M., Stollenwerk N. Analysis of an asymmetric two-strain dengue model. Math Biosci. 2014;248:128–139. doi: 10.1016/j.mbs.2013.12.009. https://www.sciencedirect.com/science/article/pii/S0025556414000030 [DOI] [PubMed] [Google Scholar]
- 61.Woodall H., Adams B. Partial cross-enhancement in models for dengue epidemiology. J Theor Biol. 2014;351:67–73. doi: 10.1016/j.jtbi.2014.02.016. https://www.sciencedirect.com/science/article/pii/S0022519314000915 [DOI] [PubMed] [Google Scholar]
- 62.Mier-y Teran-Romero L., Schwartz I.B., Cummings D.A. Breaking the symmetry: immune enhancement increases persistence of dengue viruses in the presence of asymmetric transmission rates. J Theor Biol. 2013;332:203–210. doi: 10.1016/j.jtbi.2013.04.036. https://www.sciencedirect.com/science/article/abs/pii/S002251931300204X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Aguiar M., Kooi B.W., Rocha F., Ghaffari P., Stollenwerk N. How much complexity is needed to describe the fluctuations observed in dengue hemorrhagic fever incidence data? Ecol Complex. 2013;16:31–40. https://linkinghub.elsevier.com/retrieve/pii/S1476945X12000670 [Google Scholar]
- 64.Kooi B.W., Aguiar M., Stollenwerk N. Bifurcation analysis of a family of multi-strain epidemiology models. J Comput Appl Math. 2013;252:148–158. https://www.sciencedirect.com/science/article/pii/S0377042712003305 [Google Scholar]
- 65.Reich N.G., Shrestha S., King A.A., Rohani P., Lessler J., Kalayanarooj S., et al. Interactions between serotypes of dengue highlight epidemiological impact of cross-immunity. J R Soc Interface. 2013;10(86) doi: 10.1098/rsif.2013.0414. https://royalsocietypublishing.org/doi/10.1098/rsif.2013.0414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Stollenwerk N., Aguiar M., Ballesteros S., Boto J., Kooi B., Mateus L. Dynamic noise, chaos and parameter estimation in population biology. Interface Focus. 2012;2(2):156–169. doi: 10.1098/rsfs.2011.0103. https://royalsocietypublishing.org/doi/10.1098/rsfs.2011.0103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Aguiar M., Kooi B., Martins J., Stollenwerk N. Scaling of stochasticity in dengue hemorrhagic fever epidemics. Math Model Nat Phenom. 2012;7(3):1–11. https://www.mmnp-journal.org/articles/mmnp/abs/2012/03/mmnp201273p1/mmnp201273p1.html [Google Scholar]
- 68.Aguiar M., Ballesteros S., Kooi B.W., Stollenwerk N. The role of seasonality and import in a minimalistic multi-strain dengue model capturing differences between primary and secondary infections: complex dynamics and its implications for data analysis. J Theor Biol. 2011;289:181–196. doi: 10.1016/j.jtbi.2011.08.043. https://www.sciencedirect.com/science/article/abs/pii/S0022519311004462 [DOI] [PubMed] [Google Scholar]
- 69.Wikramaratna P.S., Simmons C.P., Gupta S., Recker M. The effects of tertiary and quaternary infections on the epidemiology of dengue. PLoS ONE. 2010;5(8) doi: 10.1371/journal.pone.0012347. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0012347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Xue L., Zhang H., Sun W., Scoglio C. Transmission dynamics of multi-strain dengue virus with cross-immunity. Appl Math Comput. 2021;392 https://www.sciencedirect.com/science/article/abs/pii/S0096300320306950 [Google Scholar]
- 71.Rashkov P., Kooi B.W. Complexity of host-vector dynamics in a two-strain dengue model. J Biol Dyn. 2021;15(1):35–72. doi: 10.1080/17513758.2020.1864038. https://www.tandfonline.com/doi/full/10.1080/17513758.2020.1864038 [DOI] [PubMed] [Google Scholar]
- 72.Ghosh J.K., Ghosh U., Sarkar S. Qualitative analysis and optimal control of a two-strain dengue model with its co-infections. Int J Appl Comput Math. 2020;6(6):161. https://link.springer.com/article/10.1007%2Fs40819-020-00905-3 [Google Scholar]
- 73.Mishra A., Gakkhar S. Modeling of dengue with impact of asymptomatic infection and ADE factor. Differ Equ Dyn Syst. 2020;28(3):745–761. http://link.springer.com/10.1007/s12591-018-0436-4 [Google Scholar]
- 74.Knerer G., Currie C.S.M., Brailsford S.C. The economic impact and cost-effectiveness of combined vector-control and dengue vaccination strategies in Thailand: results from a dynamic transmission model. PLoS Negl Trop Dis. 2020;14(10) doi: 10.1371/journal.pntd.0008805. https://dx.plos.org/10.1371/journal.pntd.0008805 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Anggriani N., Tasman H., Ndii M., Supriatna A., Soewono E., Siregar E. The effect of reinfection with the same serotype on dengue transmission dynamics. Appl Math Comput. 2019;349:62–80. https://www.sciencedirect.com/science/article/abs/pii/S0096300318310695 [Google Scholar]
- 76.Bock W., Jayathunga Y. Optimal control of a multi-patch Dengue model under the influence of Wolbachia bacterium. Math Biosci. 2019;315 doi: 10.1016/j.mbs.2019.108219. https://www.sciencedirect.com/science/article/abs/pii/S0025556418303092 [DOI] [PubMed] [Google Scholar]
- 77.Shim E. Optimal dengue vaccination strategies of seropositive individuals. Math Biosci Eng. 2019;16(3):1171–1189. doi: 10.3934/mbe.2019056. http://www.aimspress.com/article/10.3934/mbe.2019056 [DOI] [PubMed] [Google Scholar]
- 78.Champagne C., Cazelles B. Comparison of stochastic and deterministic frameworks in dengue modelling. Math Biosci. 2019;310:1–12. doi: 10.1016/j.mbs.2019.01.010. https://www.sciencedirect.com/science/article/abs/pii/S0025556418301652 [DOI] [PubMed] [Google Scholar]
- 79.Mishra A., Gakkhar S. Non-linear dynamics of two-patch model incorporating secondary dengue infection. Int J Appl Comput Math. 2018;4(1):19. doi: 10.1007/s40819-017-0460-z. https://link.springer.com/article/10.1007%2Fs40819-017-0460-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Maier S.B., Huang X., Massad E., Amaku M., Burattini M.N., Greenhalgh D. Analysis of the optimal vaccination age for dengue in Brazil with a tetravalent dengue vaccine. Math Biosci. 2017;294:15–32. doi: 10.1016/j.mbs.2017.09.004. https://www.sciencedirect.com/science/article/abs/pii/S0025556416302875 [DOI] [PubMed] [Google Scholar]
- 81.González Morales N., Núñez-López M., Ramos-Castañeda J., Velasco-Hernández J. Transmission dynamics of two dengue serotypes with vaccination scenarios. Math Biosci. 2017;287:54–71. doi: 10.1016/j.mbs.2016.10.001. https://www.sciencedirect.com/science/article/abs/pii/S0025556416302401 [DOI] [PubMed] [Google Scholar]
- 82.Ndii M.Z., Allingham D., Hickson R.I., Glass K. The effect of Wolbachia on dengue dynamics in the presence of two serotypes of dengue: symmetric and asymmetric epidemiological characteristics. Epidemiol Infect. 2016;144(13):2874–2882. doi: 10.1017/S0950268816000753. https://www.cambridge.org/core/journals/epidemiology-and-infection/article/effect-of-wolbachia-on-dengue-dynamics-in-the-presence-of-two-serotypes-of-dengue-symmetric-and-asymmetric-epidemiological-characteristics/15F06CF4BCDBEE4B160EA28C72F6D12D [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Falcón-Lezama J.A., Martínez-Vega R.A., Kuri-Morales P.A., Ramos-Castañeda J., Adams B. Day-to-day population movement and the management of dengue epidemics. Bull Math Biol. 2016;78(10):2011–2033. doi: 10.1007/s11538-016-0209-6. http://link.springer.com/10.1007/s11538-016-0209-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Hendron R.-W.S., Bonsall M.B. The interplay of vaccination and vector control on small dengue networks. J Theor Biol. 2016;407:349–361. doi: 10.1016/j.jtbi.2016.07.034. https://www.sciencedirect.com/science/article/pii/S0022519316302181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Knerer G., Currie C.S.M., Brailsford S.C. Impact of combined vector-control and vaccination strategies on transmission dynamics of dengue fever: a model-based analysis. Health Care Manage Sci. 2015;18(2):205–217. doi: 10.1007/s10729-013-9263-x. https://link.springer.com/article/10.1007%2Fs10729-013-9263-x [DOI] [PubMed] [Google Scholar]
- 86.Ndii M.Z., Hickson R., Allingham D., Mercer G. Modelling the transmission dynamics of dengue in the presence of Wolbachia. Math Biosci. 2015;262:157–166. doi: 10.1016/j.mbs.2014.12.011. https://www.sciencedirect.com/science/article/abs/pii/S0025556415000164 [DOI] [PubMed] [Google Scholar]
- 87.Knipl D., Moghadas S.M. The potential impact of vaccination on the dynamics of dengue infections. Bull Math Biol. 2015;77(12):2212–2230. doi: 10.1007/s11538-015-0120-6. https://link.springer.com/article/10.1007%2Fs11538-015-0120-6 [DOI] [PubMed] [Google Scholar]
- 88.Murillo D., Holechek S.A., Murillo A.L., Sanchez F., Castillo-Chavez C. Vertical transmission in a two-strain model of dengue fever. Lett Biomath. 2014;1(2):249–271. https://lettersinbiomath.journals.publicknowledgeproject.org/index.php/lib/article/view/197 [Google Scholar]
- 89.Hu K., Thoens C., Bianco S., Edlund S., Davis M., Douglas J., et al. The effect of antibody-dependent enhancement, cross immunity, and vector population on the dynamics of dengue fever. J Theor Biol. 2013;319:62–74. doi: 10.1016/j.jtbi.2012.11.021. https://www.sciencedirect.com/science/article/abs/pii/S0022519312005966 [DOI] [PubMed] [Google Scholar]
- 90.Lourenço J., Recker M. Natural, persistent oscillations in a spatial multi-strain disease system with application to dengue. PLoS Comput Biol. 2013;9(10) doi: 10.1371/journal.pcbi.1003308. https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1003308 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Coudeville L., Garnett G.P. Transmission dynamics of the four dengue serotypes in southern Vietnam and the potential impact of vaccination. PLoS ONE. 2012;7(12) doi: 10.1371/journal.pone.0051244. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0051244 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Lourenço J., Recker M. Viral and epidemiological determinants of the invasion dynamics of novel dengue genotypes. PLoS Negl Trop Dis. 2010;4(11):e894. doi: 10.1371/journal.pntd.0000894. https://journals.plos.org/plosntds/article?id=10.1371/journal.pntd.0000894 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Kanumoori D.S.S.M., Prakash D.B., Vamsi D.K.K., Sanjeevi C.B. A study of within-host dynamics of dengue infection incorporating both humoral and cellular response with a time delay for production of antibodies. Comput Math Biophys. 2021;9(1):66–80. https://www.degruyter.com/document/doi/10.1515/cmb-2020-0118/html [Google Scholar]
- 94.de A. Camargo F., Adimy M., Esteva L., Métayer C., Ferreira C.P. Modeling the relationship between antibody-dependent enhancement and disease severity in secondary dengue infection. Bull Math Biol. 2021;83(8):85. doi: 10.1007/s11538-021-00919-y. https://link.springer.com/article/10.1007%2Fs11538-021-00919-y [DOI] [PubMed] [Google Scholar]
- 95.Thibodeaux J.J., Nuñez D., Rivera A. A generalized within-host model of dengue infection with a non-constant monocyte production rate. J Biol Dyn. 2020;14(1):143–161. doi: 10.1080/17513758.2020.1733678. https://www.tandfonline.com/doi/full/10.1080/17513758.2020.1733678 [DOI] [PubMed] [Google Scholar]
- 96.Gulbudak H., Browne C.J. Infection severity across scales in multi-strain immuno-epidemiological Dengue model structured by host antibody level. J Math Biol. 2020;80(6):1803–1843. doi: 10.1007/s00285-020-01480-3. https://link.springer.com/article/10.1007%2Fs00285-020-01480-3 [DOI] [PubMed] [Google Scholar]
- 97.Tang B., Xiao Y., Sander B., Kulkarni M.A., RADAM-LAC Research Team, Wu J. Modelling the impact of antibody-dependent enhancement on disease severity of Zika virus and dengue virus sequential and co-infection. R Soc Open Sci. 2020;7(4) doi: 10.1098/rsos.191749. https://royalsocietypublishing.org/doi/10.1098/rsos.191749 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Borisov M., Dimitriu G., Rashkov P. Modelling the host immune response to mature and immature dengue viruses. Bull Math Biol. 2019;81(12):4951–4976. doi: 10.1007/s11538-019-00664-3. https://link.springer.com/article/10.1007%2Fs11538-019-00664-3 [DOI] [PubMed] [Google Scholar]
- 99.Mapder T., Clifford S., Aaskov J., Burrage K. A population of bang-bang switches of defective interfering particles makes within-host dynamics of dengue virus controllable. PLoS Comput Biol. 2019;15(11) doi: 10.1371/journal.pcbi.1006668. https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1006668 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Nikin-Beers R., Blackwood J.C., Childs L.M., Ciupe S.M. Unraveling within-host signatures of dengue infection at the population level. J Theor Biol. 2018;446:79–86. doi: 10.1016/j.jtbi.2018.03.004. https://www.sciencedirect.com/science/article/abs/pii/S0022519318301188 [DOI] [PubMed] [Google Scholar]
- 101.ten Bosch Q.A., Clapham H.E., Lambrechts L., Duong V., Buchy P., Althouse B.M., et al. Contributions from the silent majority dominate dengue virus transmission. PLoS Pathog. 2018;14(5) doi: 10.1371/journal.ppat.1006965. https://journals.plos.org/plospathogens/article?id=10.1371/journal.ppat.1006965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Perera S.D., Perera S.S.N. Simulation model for dynamics of dengue with innate and humoral immune responses. Comput Math Methods Med. 2018;2018:1–18. doi: 10.1155/2018/8798057. https://www.hindawi.com/journals/cmmm/2018/8798057/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Ben-Shachar R., Koelle K. Transmission-clearance trade-offs indicate that dengue virulence evolution depends on epidemiological context. Nat Commun. 2018;9(1):2355. doi: 10.1038/s41467-018-04595-w. http://www.nature.com/articles/s41467-018-04595-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Mishra A., Gakkhar S. A micro-epidemic model for primary dengue infection. Commun Nonlinear Sci Numer Simul. 2017;47:426–437. https://www.sciencedirect.com/science/article/abs/pii/S1007570416304944 [Google Scholar]
- 105.Thibodeaux J.J., Hennessey M. A within-host model of dengue infection with a non-constant monocyte production rate. Appl Math. 2016;07(18):2382–2393. doi: 10.1080/17513758.2020.1733678. https://www.scirp.org/journal/paperinformation.aspx?paperid=72929 [DOI] [PubMed] [Google Scholar]
- 106.Clapham H.E., Quyen T.H., Kien D.T.H., Dorigatti I., Simmons C.P., Ferguson N.M. Modelling virus and antibody dynamics during dengue virus infection suggests a role for antibody in virus clearance. PLoS Comput Biol. 2016;12(5) doi: 10.1371/journal.pcbi.1004951. https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1004951 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Ben-Shachar R., Schmidler S., Koelle K. Drivers of inter-individual variation in dengue viral load dynamics. PLoS Comput Biol. 2016;12(11) doi: 10.1371/journal.pcbi.1005194. https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1005194 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Nikin-Beers R., Ciupe S.M. The role of antibody in enhancing dengue virus infection. Math Biosci. 2015;263:83–92. doi: 10.1016/j.mbs.2015.02.004. https://www.sciencedirect.com/science/article/abs/pii/S0025556415000371 [DOI] [PubMed] [Google Scholar]
- 109.Ben-Shachar R., Koelle K. Minimal within-host dengue models highlight the specific roles of the immune response in primary and secondary dengue infections. J R Soc Interface. 2015;12(103) doi: 10.1098/rsif.2014.0886. https://royalsocietypublishing.org/doi/10.1098/rsif.2014.0886 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Clapham H.E., Tricou V., Van Vinh Chau N., Simmons C.P., Ferguson N.M. Within-host viral dynamics of dengue serotype 1 infection. J R Soc Interface. 2014;11(96) doi: 10.1098/rsif.2014.0094. https://royalsocietypublishing.org/doi/10.1098/rsif.2014.0094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Rocha F., Aguiar M., Souza M., Stollenwerk N. Understanding the effect of vector dynamics in epidemic models using center manifold analysis. AIP Conf Proc. 2012;1479:1319. doi: 10.1063/1.4756398. http://aip.scitation.org/doi/abs/10.1063/1.4756398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Rocha F., Aguiar M., Souza M., Stollenwerk N. In: Proceedings of 12th conference on computational and mathematical methods in science and engineering. Vigo-Aguiar J., et al., editors. CMMSE; Salamanca: 2012. Mosquitos donot matter dynamically in some vector borne disease epidemiologies; pp. 1047–1062.https://cmmse.usal.es/cmmse2021/sites/default/files/volumes/3-cmmse-2012.pdf [Google Scholar]
- 113.Rocha F., Aguiar M., Souza M., Stollenwerk N. Time-scale separation and centre manifold analysis describing vector-borne disease dynamics. Int J Comput Math. 2013;90(10):2105–2125. https://www.tandfonline.com/doi/abs/10.1080/00207160.2013.783208 [Google Scholar]
- 114.Rocha F., Mateus L., Skwara U., Aguiar M., Stollenwerk N. Understanding dengue fever dynamics: a study of seasonality in vector-borne disease models. Int J Comput Math. 2016;93(8):1405–1422. https://www.tandfonline.com/doi/full/10.1080/00207160.2015.1050961 [Google Scholar]
- 115.Morrison A.C., Zielinski-Gutierrez E., Scott T.W., Rosenberg R. Defining challenges and proposing solutions for control of the virus vector Aedes aegypti. PLoS Med. 2008;5(3):e68. doi: 10.1371/journal.pmed.0050068. https://dx.plos.org/10.1371/journal.pmed.0050068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Achee N.L., Gould F., Perkins T.A., Reiner R.C., Morrison A.C., Ritchie S.A., et al. A critical assessment of vector control for dengue prevention. PLoS Negl Trop Dis. 2015;9(5) doi: 10.1371/journal.pntd.0003655. https://dx.plos.org/10.1371/journal.pntd.0003655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Ferguson N., Anderson R., Gupta S. The effect of antibody-dependent enhancement on the transmission dynamics and persistence of multiple-strain pathogens. Proc Natl Acad Sci. 1999;96(2):790–794. doi: 10.1073/pnas.96.2.790. https://www.pnas.org/content/96/2/790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Billings L., Schwartz I.B., Shaw L.B., McCrary M., Burke D.S., Cummings D.A. Instabilities in multiserotype disease models with antibody-dependent enhancement. J Theor Biol. 2007;246(1):18–27. doi: 10.1016/j.jtbi.2006.12.023. https://www.sciencedirect.com/science/article/abs/pii/S0022519306005923 [DOI] [PubMed] [Google Scholar]
- 119.Aguiar M., Kooi B., Stollenwerk N. Epidemiology of dengue fever: a model with temporary cross-immunity and possible secondary infection shows bifurcations and chaotic behaviour in wide parameter regions. Math Model Nat Phenom. 2008;3(4):48–70. https://www.mmnp-journal.org/articles/mmnp/abs/2008/04/mmnp20084p48/mmnp20084p48.html [Google Scholar]
- 120.Aguiar M., Stollenwerk N., Kooi B.W. Torus bifurcations, isolas and chaotic attractors in a simple dengue fever model with ADE and temporary cross immunity. Int J Comput Math. 2009;86(10–11):1867–1877. http://www.tandfonline.com/doi/abs/10.1080/00207160902783532 [Google Scholar]
- 121.Adams B., Holmes E.C., Zhang C., Mammen M.P., Nimmannitya S., Kalayanarooj S., et al. Cross-protective immunity can account for the alternating epidemic pattern of dengue virus serotypes circulating in Bangkok. Proc Natl Acad Sci. 2006;103(38):14234–14239. doi: 10.1073/pnas.0602768103. https://www.pnas.org/content/103/38/14234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Sabin A.B. Research on dengue during World War II 1. Am J Trop Med Hyg. 1952;1(1):30–50. doi: 10.4269/ajtmh.1952.1.30. https://ajtmh.org/doi/10.4269/ajtmh.1952.1.30https://pubmed.ncbi.nlm.nih.gov/14903434/ [DOI] [PubMed] [Google Scholar]
- 123.Waggoner J.J., Balmaseda A., Gresh L., Sahoo M.K., Montoya M., Wang C., et al. Homotypic dengue virus reinfections in nicaraguan children. J Infect Dis. 2016;214(7):986–993. doi: 10.1093/infdis/jiw099. https://academic.oup.com/jid/article/214/7/986/2388004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Lenhart S., Workman J.T. Chapman and Hall/CRC; New York: 2007. Optimal control applied to biological models. [Google Scholar]
- 125.Pontryagin L.S., Boltyanskii V.G., Gamkrelize R.V., Mishchenko E.F. Wiley; New York: 1962. The mathematical theory of optimal processes. [Google Scholar]
- 126.Nuraini N., Tasman H., Soewono E., Sidarto K.A. A with-in host Dengue infection model with immune response. Math Comput Model. 2009;49(5–6):1148–1155. https://www.sciencedirect.com/science/article/pii/S0895717708002732 [Google Scholar]
- 127.Ansari H., Hesaaraki M. A with-in host dengue infection model with immune response and Beddington-DeAngelis incidence rate. Appl Math. 2012;03(02):177–184. https://www.scirp.org/journal/paperinformation.aspx?paperid=17396 [Google Scholar]
- 128.Katze M.G., He Y., Gale M. Viruses and interferon: a fight for supremacy. Nat Rev Immunol. 2002;2(9):675–687. doi: 10.1038/nri888. http://www.nature.com/articles/nri888 [DOI] [PubMed] [Google Scholar]
- 129.Savarino A., Boelaert J.R., Cassone A., Majori G., Cauda R. Effects of chloroquine on viral infections: an old drug against today's diseases. Lancet Infect Dis. 2003;3(11):722–727. doi: 10.1016/S1473-3099(03)00806-5. https://www.thelancet.com/journals/laninf/article/PIIS1473-3099(03)00806-5/fulltext [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Décembre E., Assil S., Hillaire M.L.B., Dejnirattisai W., Mongkolsapaya J., Screaton G.R., et al. Sensing of immature particles produced by dengue virus infected cells induces an antiviral response by plasmacytoid dendritic cells. PLoS Pathog. 2014;10(10) doi: 10.1371/journal.ppat.1004434. https://journals.plos.org/plospathogens/article?id=10.1371/journal.ppat.1004434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Strauss J.H., Strauss E.G. Viruses and human disease. second edition. Elsevier; 2008. Subviral agents; pp. 345–368. [Google Scholar]
- 132.Wang W., Chen H., Yang C., Hsieh S., Juan C., Chang S., et al. Slower rates of clearance of viral load and virus-containing immune complexes in patients with dengue hemorrhagic fever. Clin Infect Dis. 2006;43(8):1023–1030. doi: 10.1086/507635. https://academic.oup.com/cid/article/43/8/1023/341720 [DOI] [PubMed] [Google Scholar]
- 133.Ridwan R. COVID-19 and dengue: a deadly duo. Trop Doct. 2020;50(3):270–272. doi: 10.1177/0049475520936874. http://journals.sagepub.com/doi/10.1177/0049475520936874 [DOI] [PubMed] [Google Scholar]
- 134.Nacher M., Douine M., Gaillet M., Flamand C., Rousset D., Rousseau C., et al. Simultaneous dengue and COVID-19 epidemics: difficult days ahead? PLoS Negl Trop Dis. 2020;14(8) doi: 10.1371/journal.pntd.0008426. https://journals.plos.org/plosntds/article?id=10.1371/journal.pntd.0008426 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Saavedra-Velasco M., Chiara-Chilet C., Pichardo-Rodriguez R., Grandez-Urbina A., Inga-Berrospi F. Coinfección entre dengue y COVID-19: Necesidad de abordaje en zonas endémicas. Rev Fac Cienc Méd Córdoba. 2020;77(1):52–54. doi: 10.31053/1853.0605.v77.n1.28031. https://revistas.unc.edu.ar/index.php/med/article/view/28031 [DOI] [PubMed] [Google Scholar]
- 136.Lorenz C., Azevedo T.S., Chiaravalloti-Neto F. COVID-19 and dengue fever: a dangerous combination for the health system in Brazil. Trav Med Infect Dis. 2020;35(March) doi: 10.1016/j.tmaid.2020.101659. https://www.sciencedirect.com/science/article/pii/S1477893920301277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Wilder-Smith A., Tissera H., Ooi E.E., Coloma J., Scott T.W., Gubler D.J. Preventing dengue epidemics during the COVID-19 pandemic. Am J Trop Med Hyg. 2020;103(2):570–571. doi: 10.4269/ajtmh.20-0480. https://ajtmh.org/doi/10.4269/ajtmh.20-0480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Joob B., Wiwanitkit V. COVID-19 can present with a rash and be mistaken for dengue. J Am Acad Dermatol. 2020;82(5):e177. doi: 10.1016/j.jaad.2020.03.036. https://www.jaad.org/article/S0190-9622(20)30454-0/fulltext [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Vasquez-Chavesta A.Z., Morán-Mariños C., Rodrigo-Gallardo P.K., Toro-Huamanchumo C.J. COVID-19 and dengue: pushing the peruvian health care system over the edge. Trav Med Infect Dis. 2020;36(April) doi: 10.1016/j.tmaid.2020.101808. https://www.sciencedirect.com/science/article/pii/S1477893920303045?via%3Dihub [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Miah M.A., Husna A. Coinfection, coepidemics of COVID-19, and dengue in dengue-endemic countries: a serious health concern. J Med Virol. 2021;93(1):161–162. doi: 10.1002/jmv.26269. https://onlinelibrary.wiley.com/doi/10.1002/jmv.26269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Aborode A.T., Corriero A.C., Fajemisin E.A., Hasan M.M., Kazmi S.K., Olajiga O. Dengue and Coronavirus disease (COVID-19) syndemic: double threat to an overburdened healthcare system in Africa. Int J Health Plann Manage. 2021:1–4. doi: 10.1002/hpm.3334. https://onlinelibrary.wiley.com/doi/10.1002/hpm.3334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Rajeshwari K.G., Abhinaya H., Brunda M.S., Mohan A. Dengue in COVID 19 pandemic year 2020- enquiry into the unanswered question of 2020? Indian J Microbiol Res. 2021;8(2):123–127. https://ijmronline.org/article-details/14424 [Google Scholar]
- 143.Panda P.K., Sharawat I.K. COVID-19 and/with dengue infection: a curse in an overburdened healthcare system. Trop Doct. 2021;51(1):106–108. doi: 10.1177/0049475520975945. http://journals.sagepub.com/doi/10.1177/0049475520975945 [DOI] [PubMed] [Google Scholar]
- 144.Cardona-Ospina J.A., Arteaga-Livias K., Villamil-Gómez W.E., Pérez-Díaz C.E., Katterine Bonilla-Aldana D., Mondragon-Cardona Á., et al. Dengue and COVID-19, overlapping epidemics? An analysis from Colombia. J Med Virol. 2021;93(1):522–527. doi: 10.1002/jmv.26194. https://onlinelibrary.wiley.com/doi/10.1002/jmv.26194 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Haqqi A., Awan U.A., Ali M., Saqib M.A.N., Ahmed H., Afzal M.S. COVID-19 and dengue virus coepidemics in Pakistan: a dangerous combination for an overburdened healthcare system. J Med Virol. 2021;93(1):80–82. doi: 10.1002/jmv.26144. https://onlinelibrary.wiley.com/doi/10.1002/jmv.26144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Milagres T.d.F., da Silva W.J., de Lemos A.B., Pilz Júnior H.L., Prophiro J.S., da Silva O.S. The co-epidemic of Dengue and COVID-19 in Brazil: between challenges in their management and the consequences of socioeconomic inequality. Res Soc Dev. 2021;10(5) https://rsdjournal.org/index.php/rsd/article/view/14728 [Google Scholar]
- 147.Widyantoro W., Nurjazuli, Hanani Darundiati Y. Implication of social restrictions on Covid-19 pandemic towards dengue control: literature review. E3S Web Conf. 2021;317:01086. https://www.e3s-conferences.org/10.1051/e3sconf/202131701086 [Google Scholar]
- 148.Harapan H., Ryan M., Yohan B., Abidin R.S., Nainu F., Rakib A., et al. Covid-19 and dengue: double punches for dengue-endemic countries in Asia. Rev Med Virol. 2021;31(2) doi: 10.1002/rmv.2161. https://onlinelibrary.wiley.com/doi/10.1002/rmv.2161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Tsheten T., Clements A.C., Gray D.J., Adhikary R.K., Wangdi K. Clinical features and outcomes of COVID-19 and dengue co-infection: a systematic review. BMC Infect Dis. 2021;21(1):1–9. doi: 10.1186/s12879-021-06409-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Verduyn M., Allou N., Gazaille V., Andre M., Desroche T., Jaffar M.-C.C., et al. Co-infection of dengue and COVID-19: a case report. PLoS Negl Trop Dis. 2020;14(8) doi: 10.1371/journal.pntd.0008476. https://journals.plos.org/plosntds/article?id=10.1371/journal.pntd.0008476 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Bicudo N., Bicudo E., Costa J.D., Castro J.A.L.P., Barra G.B. Co-infection of SARS-CoV-2 and dengue virus: a clinical challenge. Braz J Infect Dis. 2020;24(5):452–454. doi: 10.1016/j.bjid.2020.07.008. https://www.sciencedirect.com/science/article/pii/S1413867020301070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Sánhez-de la Cruz J.P., Tovilla-Zárate C.A., González-Morales D.L., González-Castro T.B. Risk of a syndemic between COVID-19 and dengue fever in southern Mexico. Gac Méx. 2020;156(5) doi: 10.24875/GMM.M20000449. http://gacetamedicademexico.com/frame_esp.php?id=476 [DOI] [PubMed] [Google Scholar]
- 153.Agudelo Rojas O.L., Tello-Cajiao M.E., Rosso F. Challenges of dengue and coronavirus disease 2019 coinfection: two case reports. J Med Case Rep. 2021;15(1):439. doi: 10.1186/s13256-021-02973-5. https://jmedicalcasereports.biomedcentral.com/articles/10.1186/s13256-021-02973-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Wahiduzzaman M., Rahim M.A. Possible re-infection of SARS-CoV-2 complicated by dengue virus co-infection: report of a rare case from Bangladesh. BIRDEM Med J. 2020:105–106. https://www.banglajol.info/index.php/BIRDEM/article/view/50993 [Google Scholar]
- 155.Hilmy A.I., Dey R.K., Imad H.A., Yoosuf A.A., Nazeem A., Latheef A.A. Coronavirus disease 2019 and dengue: two case reports. J Med Case Rep. 2021;15(1):171. doi: 10.1186/s13256-021-02707-7. https://jmedicalcasereports.biomedcentral.com/articles/10.1186/s13256-021-02707-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Hossain M.R., Sarmin M., Rahman H., Shahrin L., Nyma Z., Ahmed T., et al. SARS-CoV-2 and dengue virus coinfection in an adult with beta-thalassemia (trait): a case report from Bangladesh with literature review. Heliyon. 2021;7(10) doi: 10.1016/j.heliyon.2021.e08229. https://www.cell.com/heliyon/fulltext/S2405-8440(21)02332-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Schulte H.L., Brito-Sousa J.D., Lacerda M.V.G., Naves L.A., de Gois E.T., Fernandes M.S., et al. SARS-CoV-2/DENV co-infection: a series of cases from the Federal District, Midwestern Brazil. BMC Infect Dis. 2021;21(1):727. doi: 10.1186/s12879-021-06456-2. https://bmcinfectdis.biomedcentral.com/articles/10.1186/s12879-021-06456-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Yan G., Lee C.K., Lam L.T.M., Yan B., Chua Y.X., Lim A.Y.N., et al. Covert COVID-19 and false-positive dengue serology in Singapore. Lancet Infect Dis. 2020;20(5):536. doi: 10.1016/S1473-3099(20)30158-4. https://www.thelancet.com/journals/laninf/article/PIIS1473-3099(20)30158-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159.Omame A., Rwezaura H., Diagne M.L., Inyama S.C., Tchuenche J.M. COVID-19 and dengue co-infection in Brazil: optimal control and cost-effectiveness analysis. Eur Phys J Plus. 2021;136(10):1090. doi: 10.1140/epjp/s13360-021-02030-6. https://link.springer.com/article/10.1140%2Fepjp%2Fs13360-021-02030-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.ul Rehman A., Singh R., Agarwal P. Modeling, analysis and prediction of new variants of covid-19 and dengue co-infection on complex network. Chaos Solitons Fractals. 2021;150 doi: 10.1016/j.chaos.2021.111008. https://www.sciencedirect.com/science/article/pii/S0960077921003623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Tchoumi S., Diagne M., Rwezaura H., Tchuenche J. Malaria and COVID-19 co-dynamics: a mathematical model and optimal control. Appl Math Model. 2021;99:294–327. doi: 10.1016/j.apm.2021.06.016. https://www.sciencedirect.com/science/article/pii/S0307904X21003000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Omame A., Abbas M., Onyenegecha C. A fractional-order model for COVID-19 and tuberculosis co-infection using Atangana–Baleanu derivative. Chaos Solitons Fractals. 2021;153 doi: 10.1016/j.chaos.2021.111486. https://www.sciencedirect.com/science/article/abs/pii/S0960077921008407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Hamdan N.I., Kilicman A. A fractional order SIR epidemic model for dengue transmission. Chaos Solitons Fractals. 2018;114:55–62. https://www.sciencedirect.com/science/article/abs/pii/S0960077918304144 [Google Scholar]
- 164.Owusu-Mensah I., Akinyemi L., Oduro B., Iyiola O.S. A fractional order approach to modeling and simulations of the novel COVID-19. Adv Differ Equ. 2020;2020(1) doi: 10.1186/s13662-020-03141-7. https://advancesindifferenceequations.springeropen.com/articles/10.1186/s13662-020-03141-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Aguiar M., Stollenwerk N. SHAR and effective SIR models: from dengue fever toy models to a COVID-19 fully parametrized SHARUCD framework. Commun Biomath Sci. 2020;3(1):60–89. http://journals.itb.ac.id/index.php/cbms/article/view/14123 [Google Scholar]
- 166.Cavany S.M., España G., Vazquez-Prokopec G.M., Scott T.W., Perkins A., Pettersson J.H.-O., et al. The impacts of COVID-19 mitigation on dengue virus transmission a modelling study. medRxiv. 2020:1–20. https://medrxiv.org/cgi/content/short/2020.11.17.20210211 [Google Scholar]
- 167.Brady O., Wilder-Smith A. What is the impact of lockdowns on dengue? Curr Infect Dis Rep. 2021;23(2):2. doi: 10.1007/s11908-020-00744-9. http://link.springer.com/10.1007/s11908-020-00744-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Ong S.-Q., Ahmad H., Mohd Ngesom A.M. Implications of the COVID-19 lockdown on dengue transmission in Malaysia. Infect Dis Rep. 2021;13(1):148–160. doi: 10.3390/idr13010016. https://www.mdpi.com/2036-7449/13/1/16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Jindal A., Rao S. Lockdowns to contain COVID-19 increase risk and severity of mosquito-borne disease outbreaks. https://doi.org/10.1101/2020.04.11.20061143 [Posted April 17, 2020]
- 170.Wahala W.M.P.B., de Silva A.M. The human antibody response to dengue virus infection. Viruses. 2011;3(12):2374–2395. doi: 10.3390/v3122374. https://www.mdpi.com/1999-4915/3/12/2374 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.World Health Organization WHO announces COVID-19 outbreak a pandemic. https://www.euro.who.int/en/health-topics/health-emergencies/coronavirus-covid-19/news/news/2020/3/who-announces-covid-19-outbreak-a-pandemic Retrieved from.
- 172.Aguiar M., Stollenwerk N. Condition-specific mortality risk can explain differences in COVID-19 case fatality ratios around the globe. Publ Health. 2020;188:18–20. doi: 10.1016/j.puhe.2020.08.021. https://www.sciencedirect.com/science/article/pii/S0033350620303899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Stollenwerk N., Filipe R., Mateus L., Ghaffari P., Kooi B., Halstead S., et al. In: Proceedings of the 17th international conference on computational and mathematical methods in science and engineering CMMSE-2017. Vigo-Aguiar J., editor. CMMSE; 2017. Effective parameters, likelihoods and Bayesian model selection in application to epidemiological models: from SHAR to effective SIR models; pp. 1937–1950.https://cmmse.usal.es/cmmse2018/sites/default/files/volumes/Proceedings_CMMSE_2017_vol_1_6.pdf [Google Scholar]
- 174.Halstead S.B., Katzelnick L. COVID-19 vaccines: should we fear ADE? J Infect Dis. 2020;222(12):1946–1950. doi: 10.1093/infdis/jiaa518. https://academic.oup.com/jid/article/222/12/1946/5891764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Sánchez-Zuno G.A., Matuz-Flores M.G., González-Estevez G., Nicoletti F., Turrubiates-Hernández F.J., Mangano K., et al. A review: antibody-dependent enhancement in COVID-19: the not so friendly side of antibodies. Int J Immunopathol Pharmacol. 2021;35 doi: 10.1177/20587384211050199. https://journals.sagepub.com/doi/10.1177/20587384211050199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.Aguiar M., Ortuondo E.M., Bidaurrazaga Van-Dierdonck J., Mar J., Stollenwerk N. Modelling COVID 19 in the Basque Country from introduction to control measure response. Sci Rep. 2020;10(1) doi: 10.1038/s41598-020-74386-1. https://www.nature.com/articles/s41598-020-74386-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.COVID-19 SHARUCD dashboard. https://maira-aguiar.eu/covid19_dashboard/ Retrieved from.
- 178.Aguiar M., Van-Dierdonck J.B., Stollenwerk N. Reproduction ratio and growth rates: measures for an unfolding pandemic. PLoS ONE. 2020;15(7) doi: 10.1371/journal.pone.0236620. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0236620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179.Aguiar M., Van-Dierdonck J.B., Mar J., Stollenwerk N. The role of mild and asymptomatic infections on COVID-19 vaccines performance: a modeling study. J Adv Res. 2021 doi: 10.1016/j.jare.2021.10.012. https://www.sciencedirect.com/science/article/pii/S2090123221002083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180.Bellomo N., Bingham R., Chaplain M.A., Dosi G., Forni G., Knopoff D.A., et al. A multiscale model of virus pandemic: heterogeneous interactive entities in a globally connected world. Math Models Methods Appl Sci. 2020;30(08):1591–1651. doi: 10.1142/s0218202520500323. https://www.worldscientific.com/doi/abs/10.1142/S0218202520500323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181.Aguiar M., Dosi G., Knopoff D.A., Virgillito M.E. A multiscale network-based model of contagion dynamics: heterogeneity, spatial distancing and vaccination. Math Models Methods Appl Sci. 2021:1–30. https://www.worldscientific.com/doi/abs/10.1142/S0218202521500524 [Google Scholar]
- 182.Aguiar M., Van-Dierdonck J.B., Mar J., Cusimano N., Knopoff D., Anam V., et al. Critical fluctuations in epidemic models explain COVID-19 post-lockdown dynamics. Sci Rep. 2021;11(1) doi: 10.1038/s41598-021-93366-7. http://www.nature.com/articles/s41598-021-93366-7 [DOI] [PMC free article] [PubMed] [Google Scholar]