High-Fidelity Capture, Threading and Infinite-Depth Sequencing of Single DNA Molecules with a Double-Nanopore System

Abstract

Nanopore sequencing of nucleic acids has an illustrious history of innovations that eventually made commercial nanopore sequencing possible. Nevertheless, the present nanopore sequencing technology leaves much room for improvement, especially with respect to accuracy of raw reads and detection of nucleotide modifications. Double-nanopore sequencing—an approach where a DNA molecule is pulled back and forth by a tug-of-war of two nanopores—could potentially improve single molecule read accuracy and modification detection by offering multiple reads of the same DNA fragment. One principle difficulty in realizing such a technology is threading single-stranded DNA through both nanopores. Here, we describe and demonstrate through simulations a nanofluidic system for loading and threading DNA strands through a double-nanopore setup with nearly 100% fidelity. The high-efficiency loading is realized by using hourglass-shaped side channels that not only deliver the molecules to the nanopore but also retain molecules that missed the nanopore at the first passage to attempt the nanopore capture again. The second nanopore capture is facilitated by an orthogonal microfluidic flow that unravels the molecule captured by the first nanopore and delivers it to the capture volume of the second nanopore. We demonstrate potential utility of our double nanopore system for DNA sequencing by simulating repeat back-and- forth motion—flossing—of a DNA strand through the double nanopore system. We show that repeat exposure of the same DNA fragments to the nanopore sensing volume considerably increases accuracy of the nucleotide sequence determination, and that correlated displacement of ssDNA through the two nanopores may facilitate recognition of homopolymer fragments.

Graphical Abstract

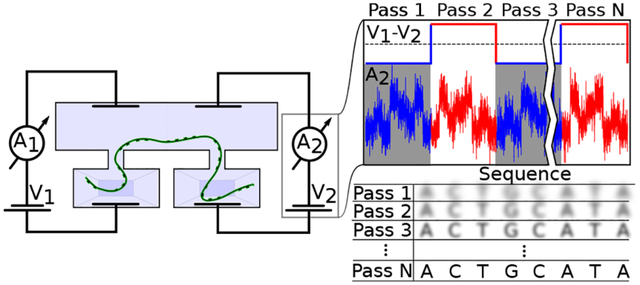
Nanopore sensing^1,2 and sequencing^3,4 rely on the partial blockade of ionic current flowing through a nanopore for detection and identification of biomolecules.⁵ For globular biomolecules, which includes the majority of folded proteins and some RNA, a nanopore sensor operates similar to a Coulter counter,⁶ where the passage of individual biomolecules produces ionic current transients characterized by well-defined depth and width.⁷ Nanopore translocation of a nucleic acid polymer produces much more complex signatures,^8,9 which nevertheless can be transcribed¹⁰ into the nucleotide sequence of the polymer.¹¹

One problem with conventional nanopore sensing is that one gets to measure the signal from a passing analyte only once, which severely limits fidelity of the analyte identification. Two types of approaches have been described to extend the exposure of an analyte to the nanopore current characterization: reducing the speed of the nanopore translocation or capturing the same molecule more than once by a nanopore. While many diverse approaches have been devised to transiently arrest nanopore transport,^12–16 measuring a nanopore signal from the same molecule has been limited to recapturing the molecule by the same nanopore¹⁷ or to passing the same molecule sequentially through two nanopores.^18–20

A double nanopore system²¹ can, potentially, enable multiple reads of the sequence of a nucleic acid polymer^22,23 or repeat measurements of the current blockade from the same protein bound to DNA.^24,25 In such a system, the electrophoretic force of the two nanopores creates a tug-of-war condition,²⁶ straightening the molecule confined between the nanopores and allowing the translocation direction to be controlled by a minute difference in the magnitude of the forces exerted by the two nanopores.²¹ First demonstrated in the form of a mechanical trap,²¹ the tug-of-war control over DNA motion was also realized in a double-barrel capillary system^24,27 and in a solid-state device²⁸ integrated with a field-programmable gate array enabling active control of the DNA translocation process.²⁹

One potential problem with using a double nanopore system for sequencing or sensing applications is the need to capture and thread a DNA or any other molecule not just through one but through two nanopores. Improving the rate of nanopore capture has long been recognized as a critical factor enabling practical applications of nanopore sensing with major breakthroughs involving the use of a salt gradient,³⁰ dielectrophoretic forces^31,32 or membrane-tethering of ssDNA.^11,33 Systems have been designed to filter and sort DNA molecules according to their size³⁴ or to alter DNA conformation prior to entering a nanopore.³⁵ Controlled DNA delivery has been realized using a glass capillary³⁶ and an optofluidic device³⁷ whereas both side solvent flow³⁸ and conical confinement³⁹ have been explored to increase efficiency of nanopore capture.

Here, we describe and demonstrate through coarse-grained and all-atom molecular dynamics simulations a double nanopore system for capturing and threading single stranded DNA (ssDNA) molecules with 100% efficiency and show how multiple reads from the same molecule improve fidelity of DNA sequence identification. Such a combination of high-fidelity loading and repeat sequencing of the same molecule may offer considerable improvements in the performance of the nanopore sequencing method with regard to nucleotide identification at a truly single-molecule level.

RESULTS

Our double nanopore system consists of three solution-filled volumes: two parallel delivery channels and a cross-flow chamber separated from the delivery channels by a thin membrane, Fig. 1. Each delivery channel is connected to the flow chamber through a nanopore located in the narrowest section of the delivery channel. The DNA is introduced at the rectangular section of the first delivery channel, Fig. 1a. The DNA is then threaded through the first and then the second nanopore with 100% efficiency, guided by the pressure and voltage differences at the inlets and outlets of the solution-filled volumes. In this study, we chose the specific geometry of the device and the operating conditions in order to keep the simulations feasible and to examine the limits of this double nanopore capture approach. A consequence of this is that the procedure described below may be experimentally difficult to replicate exactly. Nevertheless, we wish to emphasize that our double nanopore capture approach is robust to the kinds of changes that experimental considerations would require, and we will comment on these changes as they arise.

Figure 1:

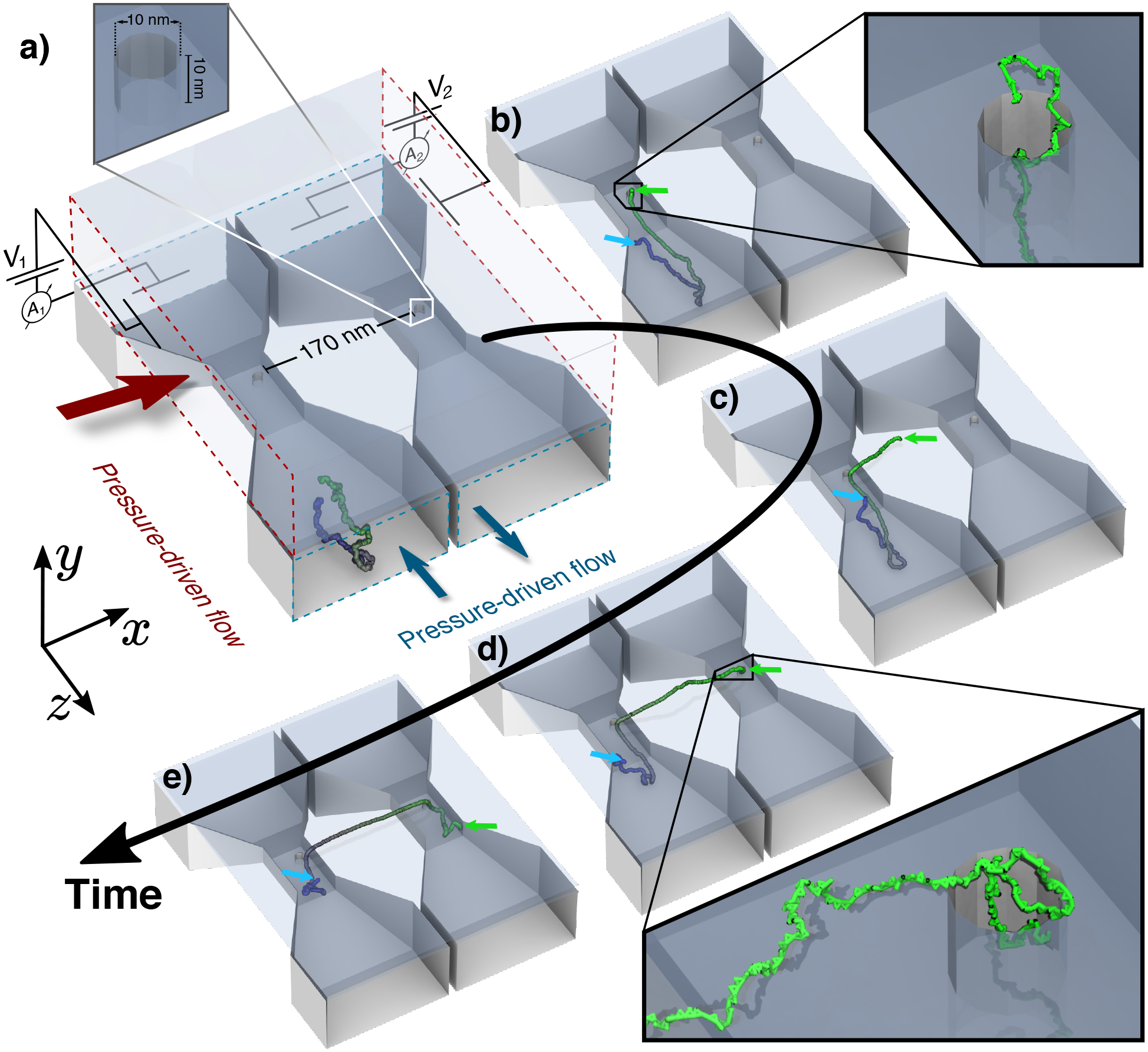
MD simulation of ssDNA threading through a double-nanopore system. (a) Initial configuration of the system. Two cross channels (aligned with the z axis) are connected to a common flow chamber (aligned with the x-z plane) through two nanopores (aligned with the y axis). The electric potential in each of the cross channels (V₁ and V₂) as well as the pressure difference in each channel (Δp₁, Δp₂) and the flow chamber (Δp_ch) can be independently controlled. The walls of the lower two delivery channels are depicted as solid surfaces, all other surfaces are semitransparent. A 1,000-nucleotide ssDNA molecule is shown using a green-to-blue color gradient. (b) Capture of ssDNA by the first nanopore. The DNA strand was driven from the inlet of a cross channel by a pressure difference Δp₁ = 0.05 atm; V₁ = −600 mV. Green and blue arrows mark the ends of ssDNA. (c) Flow-assisted delivery of ssDNA towards the second nanopore (Δp_ch = 0.2 atm; V₁ =−100 mV; V₂ = +600 mV). (d) Capture of ssDNA by the second nanopore. (e) Final configuration of ssDNA. V₁ =V₂ = +600 mV.

Figure 1a–e and Movie 1 illustrate a typical outcome of a coarse-grained molecular dynamics (MD) simulation of 1kbp ssDNA threading. Starting from a configuration shown in Fig. 1a, a pressure difference of 0.05 atm across the first delivery channel (Δp₁) transports the solvent along with the DNA towards the first nanopore. A −600 mV difference of the electric potential (V₁) between the inlet/outlet boundaries of the first delivery channel and the electrically grounded flow chamber captures the DNA from the first delivery channel into the first nanopore, Fig. 1a–b. Driven by a pressure difference of 0.2 atm (Δp_ch), the solvent flow in the flow chamber guides the end of the DNA captured by the first nanopore towards the second nanopore, where a voltage difference of 600 mV (V₂) promotes the capture of the DNA by the second nanopore, Fig. 1c–d. Having the DNA molecule threaded simultaneously through both nanopores, further motion of the DNA is halted by setting the voltage in the two delivery channels to the same positive value (V₁ = V₂ = 600 mV), which straightens the DNA confined between the two nanopores, Fig. 1e. From this configuration, the DNA molecule can be flossed back and forth through the two nanopores by a voltage differential, V₁ − V₂, and can be eventually removed from the double nanopore system by setting a non-zero pressure difference (Δp₂) across the second delivery channel.

We characterized the fidelity of the nanopore capture and threading by repeating our simulation 100 times starting from different initial conformations of 1kbp ssDNA. This DNA length was chosen as it is close to the minimum value that a device of the given nanopore spacing could reliably handle. If the middle of the DNA is caught at the first nanopore, the DNA nearly exits the first nanopore as it enters the second. This would not happen for DNA significantly longer than 1kbp, and would therefore be captured with greater ease. Note that our mechanism of high fidelity capture and threading would also work for double stranded DNA and RNA/DNA hybrid constructs upon scaling up the device dimensions to account for a larger persistence length. Our choice of simulation conditions was dictated by a ~1 V upper bound on the magnitude of voltage bias differential, with 600 mV being a typical value used in the double nanopore capture experiments.^28,29 For the pressure differentials, we explored the 0.01 to 1 atm range, which is also experimentally accessible.⁴⁰ Through all our simulations, the electric potential of the second delivery channel, V₂, was kept constant to minimize the changes in conditions required for the realization of the threading process. Thus, the capture process in our simulation was controlled by the voltage of the first delivery channel, V₁. Note that because our coarse-grained simulations neglect friction between the pore walls and the DNA, the DNA transport rates reported below should be regarded as the fast transport limit. The transport in an equivalent experimental device is expected to be slower.

First, we characterize the statistics of ssDNA capture by the first nanopore. Figure 2a,b illustrate the distribution of the electrostatic potential and of the fluid flow velocity in our double nanopore system under conditions that promote the first capture. The electrostatic potential in the first and the second delivery channels approach the −/+600 mV values prescribed at the channels’ inlets and outlets. The solvent flow through the flow chamber has the expected laminar profile whereas the flow profile in the delivery channels is more peculiar, with the fluid having a higher velocity at the channel’s constriction, where the nanopore is located, than at the inlet/outlet surfaces. Figure 2c provides a more detailed view of the flow profile in the first delivery channel along with three representative snapshots of ssDNA conformation realized during a typical simulation of ssDNA capture.

Figure 2:

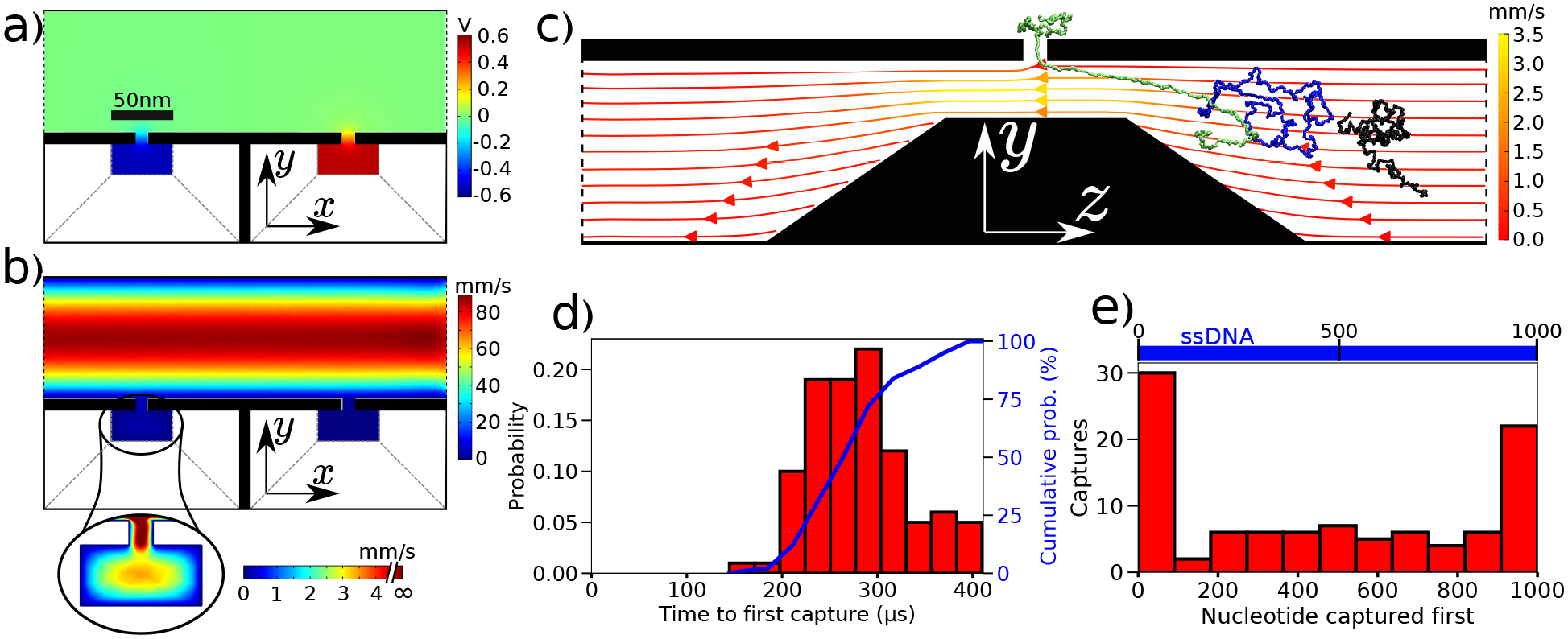
Statistics of ssDNA capture. (a,b) The electrostatic potential (panel a) and the fluid flow velocity (panel b) in the x-y cross section of the double nanopore system. The cross section passes through the two nanopores. The inset illustrates the fluid flow inside the first delivery channel. (c) Snapshots illustrating typical conformations of ssDNA (at 0 μs, black; 232 μs, blue; and 307 μs, green) during a nanopore capture in the first delivery channel. The streamlines illustrate the local direction and the magnitude of the solvent flow. (d) Normalized distribution of the time elapsed from the start of the simulation until the nanopore capture. The distribution was obtained from the analysis of 100 independent simulations that differed from one another by the initial conformation of ssDNA. The cumulative probability of nanopore capture (plotted at the right axis) reaches 100%, i.e., all 100 molecules were captured. (e) The probability of first ssDNA capture occurring at the specifying site along the DNA molecule.

The shear force of the non-uniform fluid flow combined with the gradient of the electric potential, SI Fig. S1, contribute to highly efficient capture of ssDNA by the nanopore. Although the time elapsed from the beginning of each simulation until the nanopore capture was found to have a broad distribution, Fig. 2d, the DNA capture was observed in all 100 simulations, meaning that our cross-channel system captures ssDNA with 100% efficiency. Interestingly, we observed a pronounced preference for ssDNA to be captured at its ends, with about half of all ssDNA capture events starting with capturing a DNA fragment located within the first hundred nucleotides from the DNA’s end, Fig. 2e. Similar preference for end capture was experimentally observed in single nanopore experiments performed using double-stranded DNA.⁴¹

The reported 100% efficiency of ssDNA capture has been made possible in part by the pressure difference that forced the solvent through the first delivery channel. While lowering that pressure would make it take longer for the DNA to reach the first pore, increasing the pressure could have more serious consequence: it would increase the chance for DNA to miss its opportunity to enter the nanopore. We demonstrate this directly in a simulation carried out under Δp₁ = 1 atm, Fig. 3a, where we see the ssDNA stretching and missing the nanopore entrance. Interestingly, when we restarted the simulation midway from the 1 atm trajectory at a lower, 0.75 atm pressure, we still saw the DNA missing the nanopore entrance but the DNA was not carried away from the nanopore by the flow, Fig. 3b. Rather, it became suspended a fixed distance past the nanopore entrance. Continuing the simulation at even lower pressure values, at 0.1 atm, Fig. 3c, and then at 0.05 atm, Fig. 3d, confirmed this behavior: at each pressure value, the DNA was seen to adopt a new equilibrium location past the nanopore, moving closer to the nanopore entrance at lower pressure. Figure 3e describes this behavior quantitatively by showing the pressure and the z-coordinate of the DNA center of mass as a function of simulation time. We attribute this behavior to a small yet apparently sufficient electric field that leaks out from the nanopore and into the delivery channel, Fig. 3f, and exerts a force on the DNA that cancels the force of the solvent flow. Thus, even if a DNA molecule misses the nanopore entrance (which, in experiment, would be registered as a shallow blockade of the nanopore current), the molecule is not lost and can be pulled back by lowering the pressure in the delivery channel.

Figure 3:

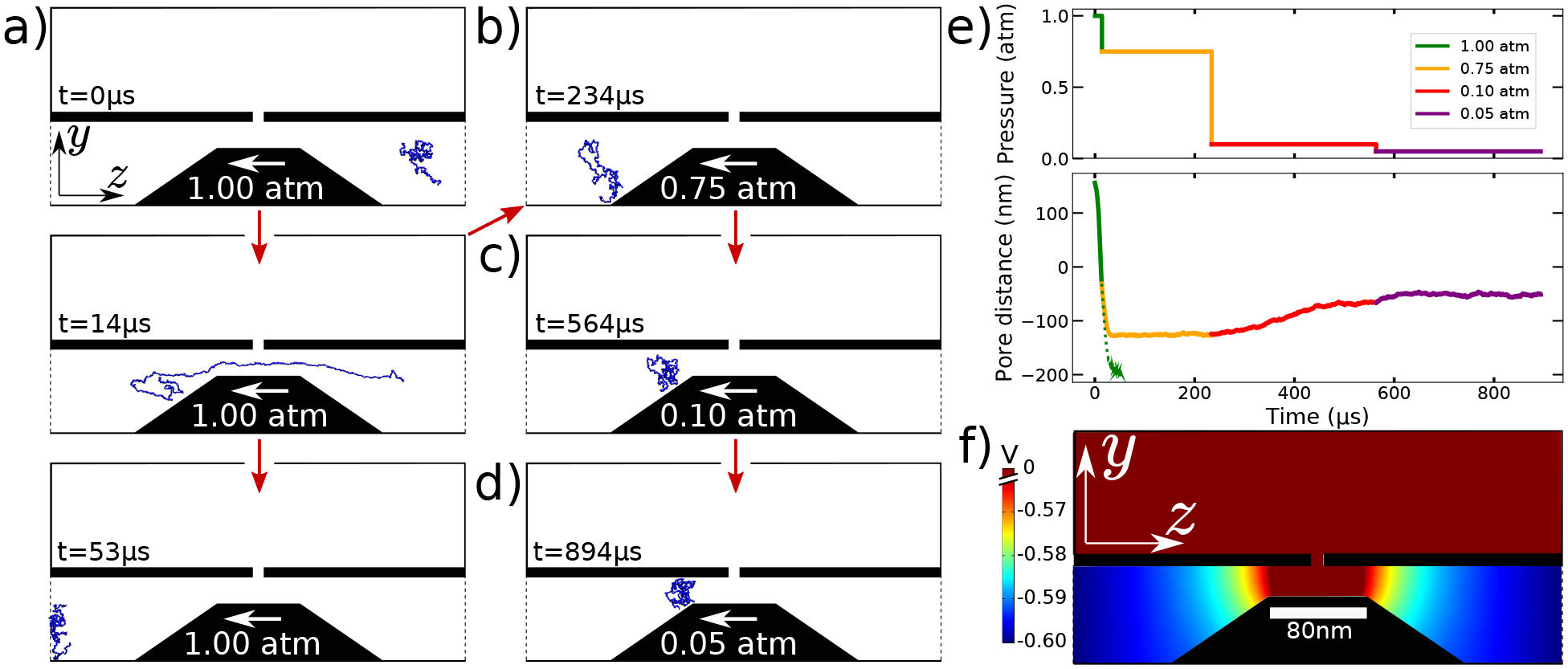
Trapping molecules that missed the nanopore entrance. (a) Snapshots illustrating ssDNA motion through the first delivery channel under Δp₁ = 1 atm. (b) After 14 μs at Δp₁= 1 atm, Δp₁ was reduced to 0.75 atm for 220 μs. (c) After 220 μs at Δp₁= 0.75 atm, Δp₁ was reduced to 0.1 atm for 330 μs. (d) After 330 μs at Δp₁= 0.1 atm, Δp₁ was reduced to 0.05 atm for another 330 μs. (e) Difference between the inlet and outlet pressure (Δp₁, top) and the distance between the DNA’s center of mass (bottom) and the nanopore as a function of simulation time. (f) Distribution of the electrostatic potential in the delivery channel.

Now we turn our attention to the second nanopore capture, which is facilitated by the fluid flow through the flow chamber. The DNA’s capture by the first nanopore is registered experimentally as a pronounced blockade of the ionic current flowing through the first nanopore.²⁹ This event can be used to adjust the experimental conditions to increase the chance of double nanopore threading. To simplify further analysis, we turned off the pressure differential and increased the potential to V₁ = −100 mV in the first delivery channel 1.5 μs after the first capture. Simply leaving the potential of the first channel at V₁ = −600 mV could push the DNA from the delivery channel into the flow chamber faster than the flow could straighten it out, thereby increasing the chance that the DNA will exit the first pore before being captured at the second, Fig. 4a. The likelihood of this outcome was exacerbated by a slower flow of solvent in the flow chamber, i.e., lower Δp_ch values. At the same time, we found that switching the first potential off (V₁ = 0) would create the conditions for the DNA to pull back into the delivery channel under the action of the entropic force⁴² from the rest of the DNA, Fig. 4b. The optimal condition for the double nanopore threading was found when the potential of the first delivery channel was not switched off completely but increased to a higher value, from −600 to −100 mV, Fig. 4c, exerting a force sufficient to counteract the entropic pull back and yet not too large to generate extra slack of ssDNA in the flow chamber.

Figure 4:

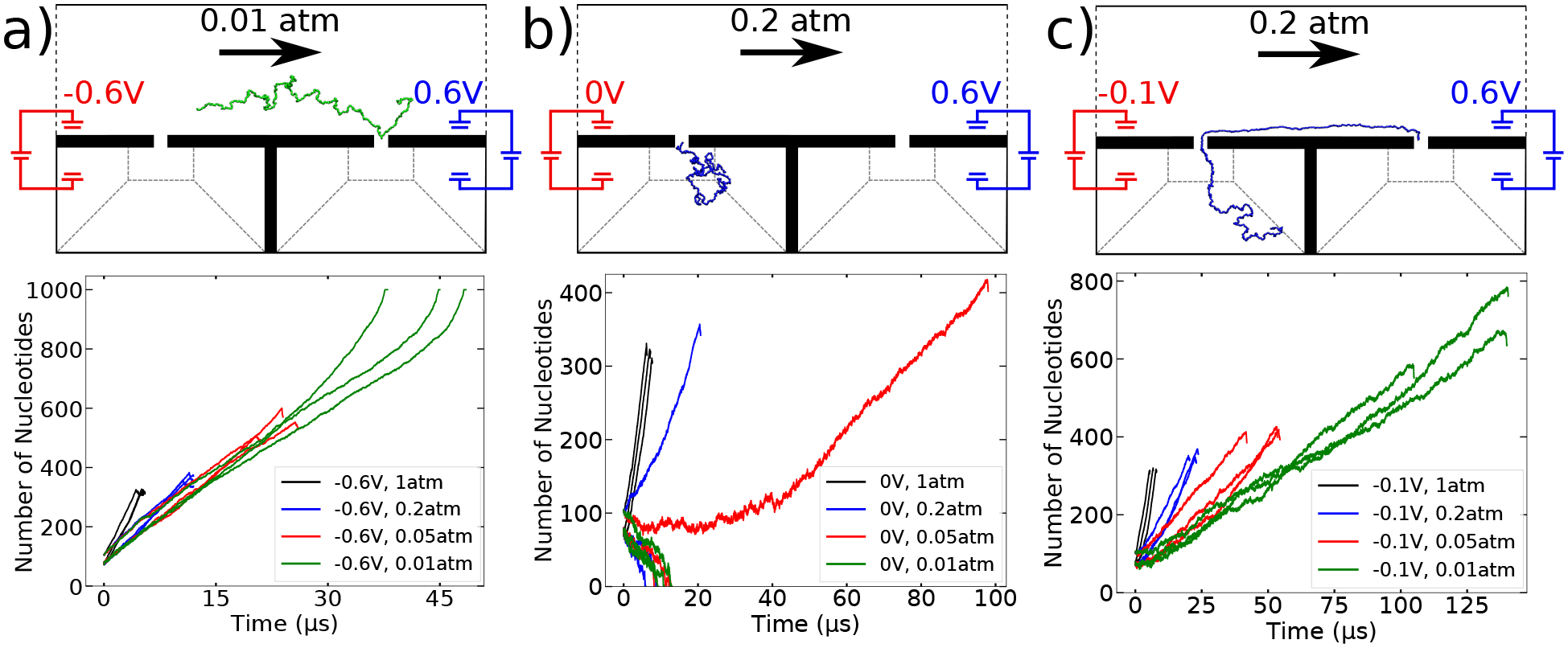
Conditions affecting second nanopore capture. (a–c) Number of DNA nucleotides in the flow chamber versus simulation time for V₁ = −600 (panel a), 0 (panel b) and and −100 (panel c) mV and the four values of Δp_ch indicated by the color of the lines. Three independent simulations were carried out for each combination of V₁ and Δp_ch. All simulations started from three different initial configurations of ssDNA each of which was end-threaded through the first nanopore.

In the above simulations, we chose to wait only 1.5 μs after the first capture before increasing the voltage to −100 mV in order to investigate the situation where entropic pullback of the DNA could result in a failed capture. Although only tens of nucleotides translocated into the flow chamber within those 1.5 μs, the DNA did not pull out, ensuring that pullback will not occur for longer reaction times either. A practical reason for changing the potential after the first capture would be to decrease the slack in the DNA prior to second capture. However, even if we do not change the potential, the second capture still occurs successfully, Fig. 4a, We note that turning off the pressure in the first delivery channel after ~1.5 μs is not required for successful experimental implementation. This is apparent from Fig. 3b–d, where we see the fluid force on the DNA in the constriction to balance the force of the electric field leaking out from the nanopore. The field inside the nanopore is about two orders of magnitude larger than the field leaking out from the nanopore, so keeping the pressure difference on in the first delivery channel will not pull the DNA back from the first nanopore or noticeably affect the process of second nanopore capture.

In selecting the pressure differential for the flow chamber, our objective was to have a flow that kept the DNA straight and against the chamber wall to maximize the likelihood that it will come near the second pore and be captured. A pressure that is too small introduces slack into the DNA, Fig. 4a. On the other hand, a pressure that is too large is also undesirable, because it decreases the time between the two captures without offering a significantly straighter conformation. Using Δp_ch = 0.2 atm in our simulations was observed to sidestep all of the above complications, Fig. 4c.

Having determined the optimal condition for capturing ssDNA by the second nanopore, we characterized the statistics of the second nanopore capture. The entrance of a DNA strand into the second nanopore is experimentally registered as a drop of the ionic current flowing through the second nanopore. Detection of such a drop will trigger a further adjustment of potential V₁, which we set in our simulation to the same value as V₂, +600 mV, 4 μs after the second capture has occurred. Additionally, we set all pressure differentials to zero. SI Fig. S2 shows the distribution of the electrostatic potential in our double nanopore system immediately before and after the second nanopore capture.

We found that second nanopore captures are naturally categorized as either end-first or folded capture. We determined the type of capture by monitoring the number of nucleotides in each of the three channels. For end-first capture, the number of nucleotides in the flow chamber rises steadily after first capture until the maximum value of roughly 330 nucleotides are inside, Fig 5a. At this point, the end of the DNA molecule is captured by the second nanopore, and the number of nucleotides in the second delivery channel rises for 4 μs, after which the electrostatic potentials are set to V₁ = V₂ = +600 mV, and the DNA is held in place with no subsequent change to the number of nucleotides in any of the chambers.

Figure 5:

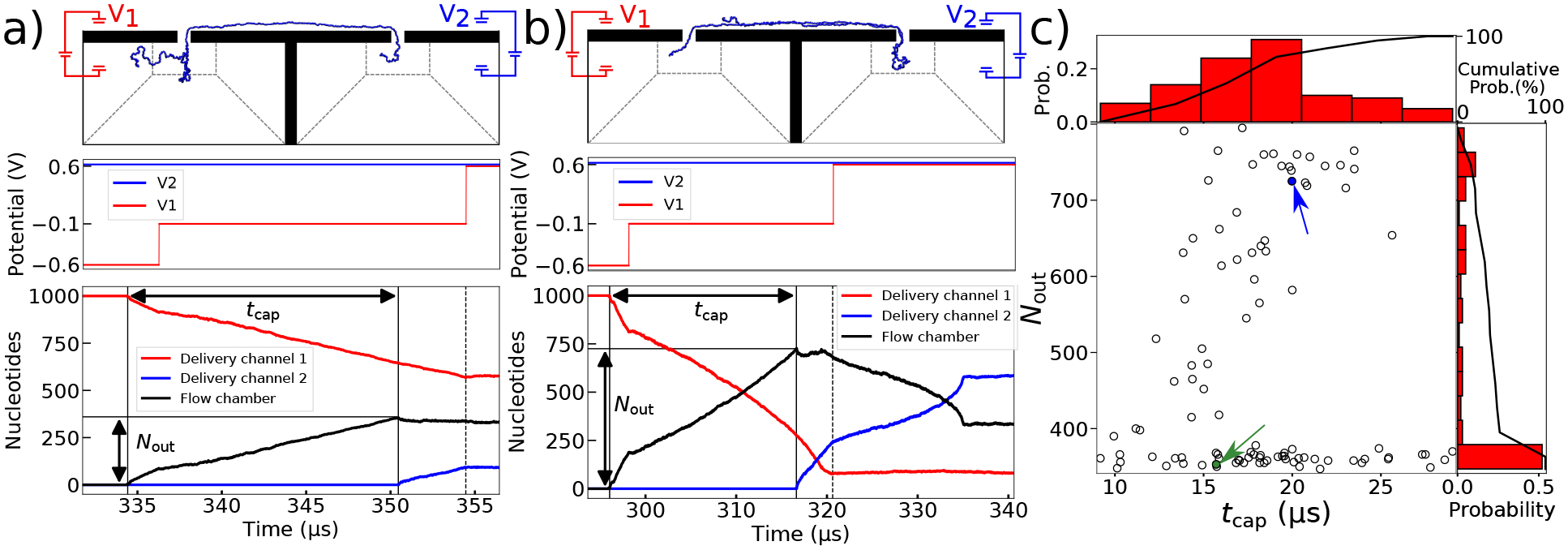
Statistics of second pore capture. (a,b) The voltage bias (top) and the number of DNA nucleotides in the delivery channels and flow chamber (bottom) versus simulation time for end-threaded capture (panel a) and for folded capture (panel b). The time between captures is denoted by t_cap and the number of nucleotides in the flow chamber at the time of second capture, N_out. The images illustrate the DNA conformation 4 μs after second capture, when V₁ is changed to 0.6 V. These times are denoted with a dashed line. (c) Scatter plot of N_out versus t_cap for all 100 simulations. The simulations marked with green and blue arrows are the ones shown in panel a and b, respectively. The histograms show the distribution of the t_cap (top) and N_out (right) values. The cumulative probability of double nanopore capture reaches 100%, i.e., all 100 molecules were simultaneously captured in both nanopores.

For folded captures, we saw that nucleotides exit the first delivery channel and enter the flow chamber at about twice the rate seen in end-first capture, Fig 5b. This signifies that the DNA molecule has folded somewhere along its length to enter the first nanopore, and that there are two fragments of the same ssDNA molecules in the first nanopore after first capture. At the time of second capture, this DNA molecule enters the second nanopore, again in a folded conformation. After 4 μs the electrostatic potentials are set to hold the DNA molecule still, but because one end of the DNA still exists in the flow chamber, we see significant adjustment to the number of nucleotides in the second delivery channel and flow chamber as the free end of the DNA is pulled through the second nanopore. While the specific location of the DNA nucleotides cannot be easily monitored so closely in experiments, the blockade currents through the nanopores can be measured to deduce the number of DNA strands translocating through each nanopore.^21,29

To understand the frequency of these different capture modes, we determined for each simulation the time between first and second capture, t_cap, and the number of nucleotides in the flow chamber at the time of second capture, N_out. The resulting scatter plot in Fig. 5c consists of a flat and linear part. The points at the lower right correspond to those DNA molecules captured by the first nanopore at the end. As the point of first capture begins to shift away from the end, the fluid pressure in the flow chamber quickly straightens out the DNA’s fold before it arrives at the second nanopore, resulting in a constant value of N_out and a reduced value of t_cap. However, as the point of first capture shifts further away from the end, the fold in the DNA cannot be fully removed in the flow chamber, resulting in the linear rise of N_out beginning in the lower left of the plot. By collapsing the scatter plot into a histogram for the value of N_out, we see that half of the simulations resulted in end-first capture and half in folded capture at the second pore. It is also worth mentioning that, although the time to first capture isn’t so well defined because it varies on the order of hundreds of μs, the histogram corresponding to t_cap shows that after the first capture, the time to second capture varies only on the order of tens of μs, and is thus far more predictable.

In the above simulations, we switched the simulation conditions 4 μs after the second capture to ensure that approximately 100 nucleotides translocated into the second delivery channel, preventing entropic pullback that could be caused by the difference in the number of nucleotides in the two delivery channels. If such a rapid change is not achieved experimentally, more DNA will translocate into the second delivery channel and make the DNA pull out even less likely. The solvent flow in the flow chamber, however, was found to produce a deterministic slip (~12.5 nt/μs) of the DNA from the first nanopore to the second even when both voltages were set to +0.6V. To prevent such slippage, switching off the flow in the flow chamber should be performed in sync with reducing the voltage differential (V₁ − V₂), the precise specifications of which will depend on the reaction time of the nanofluidic system.

For fragments of DNA significantly longer than 1kbp, it is increasingly likely that both of the ends will still be in the first delivery channel at the end of our double-nanopore capture method. Although this did not occur in any of our 100 simulations, we created a scheme to remove one end out of the first pore and into the second, SI Fig. S3. By periodically pulsing the electric potential across the first pore down from 0.6V to 0.1V to create an imbalance in the tug-of-war, the DNA slips little by little into the second pore until one end of the DNA exits the first pore, resulting in successful capture.

In order to demonstrate the changes experimentalists would have to make to employ such a double nanopore capture process, we consider the specific changes that would be needed if the nanopore spacing was increased by a factor of ten, to 1700 nm. As far as the second capture is concerned, the most obvious consequence of this change would be that the minimum length of DNA the device could sequence would also increase by a factor of ten. Furthermore, lengthening the flow chamber would make it more resistive to fluid flow. An increased applied pressure could counter this to achieve the desired fluid velocity, but if the device could not be safely put under such a pressure, the cross section of the flow chamber could be increased to reduce its resistance. With regards to the first capture, using longer DNA requires no change to the geometry of the delivery channels. This is apparent by observing the stretched conformation of the DNA in Fig. 2c. The constriction in the delivery channel serves to accelerate the flow and expand the electric field’s reach such that DNA is caught not when the center of mass of the DNA approaches the nanopore, but when a segment of the DNA begins to approach the constriction and is then stretched out and caught. This would be how DNA of any length is captured in such a device, and we therefore emphasize the importance of replicating such a constriction in experiment. Such funnel-like channels can be manufactured using the focused ion beam milling technology.³⁹

Finally, we demonstrate potential utility of our double nanopore system for DNA sequencing by considering a situation where a single DNA molecule is already threaded through two nanopores in a multilayer hexagonal boron nitride (hBN) membrane, Fig. 6. Although solid-state nanopores have long been recognized as potentially superior replacements for biological nanopores,^43–45 solid-state nanopore sequencing has remained elusive.^46,47 The most important problems are speed control and entropic conformational randomness.^48,49 We believe that both problems can be resolved using a system of two nanopores in a 2D membrane which provides both speed control by controlling the difference of the voltage drop across the two nanopores and which also drastically decreases the heterogeneity of nucleotide conformations because of the nucleotides’ adhesion to the membrane.⁵⁰

Figure 6:

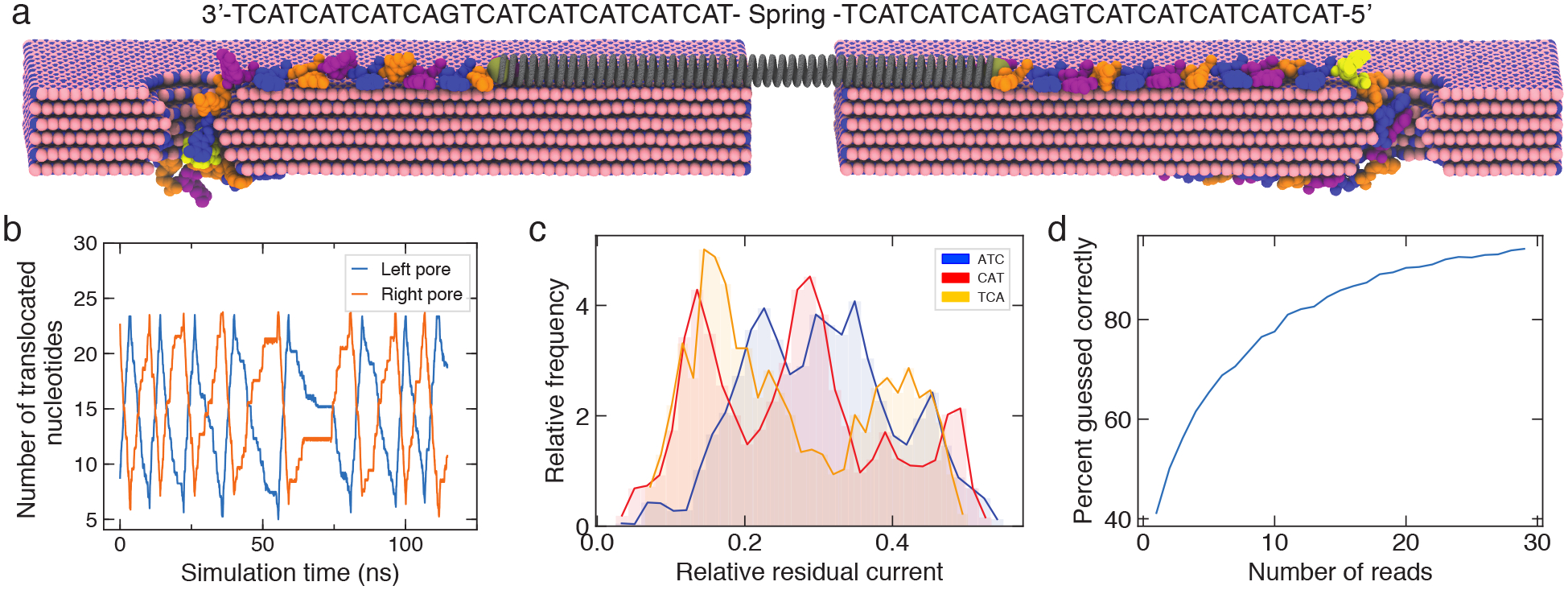
Infinite-depth sequencing of the same DNA molecule by double nanopore flossing. (a) Illustration of the simulation system, where a fragment of ssDNA is threaded through two solid-state nanopores in a 6-layer boron-nitride membrane. A virtual spring (grey) connects the DNA from two simulation systems, coupling DNA motion through both nanopores. The DNA has the repeat-triple sequence. Water and ions are not shown for clarity. DNA flossing is produced by alternatively applying a 10 V bias to either left or right pore. (b) Number of DNA nucleotides translocated through each nanopore. (c) Distribution of residual ionic current for the three nucleotide triplet present in the nanopore. Currents were computed using the steric exclusion model.⁵¹ (d) Effect of repeat reads of a triplet (due to multiple passes through the pore) on the probability of guessing the correct triplet solely from the relative residual current.

For our proof-of-principle simulations, we chose a system of two identical 1.5 nm diameter hBN nanopores which were shaped to reproduce the constriction of the MspA nanopore, the first nanopore used to experimentally demonstrate nanopore DNA sequencing.⁹ Each of the two all-atom simulation systems contained a fragment of ssDNA of triplet-repeat sequence, similar to that used by Gundlach and co-workers.⁹ The two simulations were coupled via a harmonic potential applied to the ends of the DNA, mimicking the experimental situation where the same DNA fragment is captured by two nanopores that are separated by a distance that considerably exceeds the length scale amenable to the all-atom MD method. The DNA translocation back and forth through the double nanopore system was realized by applying a voltage bias alternatively to each simulation system, reversing the translocation direction when the strand’s end reached the edge of the simulation system. Because of ssDNA adhesion to hBN surface,⁵² the DNA strand translocates through the nanopore in discrete steps,⁵⁰ with the translocation probability being an exponential function of the transmembrane bias.^50,53 Constrained by the time scale of the all-atom MD methods, we chose a transmembrane bias of 10 V for these exploratory simulations which enabled us to observe multiple back-and-forth motion of the DNA strand through the nanopores while preserving the stepwise character of the translocation process, Fig. 6b. SI Movie 2 illustrates the simulation trajectory. Repeating the simulations at a higher (20 V) and a lower (5 V) magnitude of the transmembrane potential, SI Fig. S4, confirmed the expected dependence of the translocation velocity on the bias, SI Fig. S5. Thus, lowering the magnitude of the bias differential should enable flossing ssDNA at arbitrary low speeds, which would be highly advantageous for accurate recognition of the DNA nucleotides.

Flossing of the DNA molecule through two BN nanopores repeatedly placed DNA nucleotides in statistically similar conformations. To demonstrate utility of such repeat placement, we extracted a set of DNA conformations that featured the same nucleotide triplet (ATC, CAT or TCA) in the nanopore constriction. We next used the steric exclusion model⁵¹ to compute the relative residual current for each DNA conformation and obtain the histogram of blockade currents for each nucleotide triplet, Fig. 6c. The resulting distributions exhibit considerable overlap, which we partially attribute to the extreme simulation timescale that may have precluded ssDNA nucleotides from finding an equilibrium low-energy conformation between consecutive translocation steps. Taking this worst case scenario distributions as input, we can assess the probability of correctly identifying the nucleotide triplets from the ionic current alone when they are subject to repeat nanopore ionic current measurment, Fig. 6d. With the single read identification probability being slightly better than random, the identification fidelity increases to over 90% after moving DNA back and forth tens of times.

Close examination of the 10 V simulation trajectory, Fig. 6b, suggests that the stepwise displacement of ssDNA through the two nanopores is correlated. We examined such correlated motion quantitatively by plotting the time at which each of the translocation steps occurred in each nanopore in the 5 V trajectory, SI Fig. S6. The individual translocation events through individual nanopores are found to occur within ~1 ns from one another, with only 3 uncorrelated events from 33 total stepwise displacements. Such highly correlated motion enables, in principle, accurate characterization of DNA homopolymer sequences, which is a long-standing problem for nanopore sequencing. In such a correlated motion scenario, the number of nucleotides in the homopolymer fragment passing through one nanopore could be discerned by counting the number of nucleotides from a heterogeneous-sequence fragment of the same molecule passing through the other nanopore.

CONCLUSIONS

In summary, we have described a nanofluidic double nanopore system that has the potential to considerably increase the fidelity of DNA and RNA sequencing. Upon high-fidelity loading of a single DNA or RNA molecule into two pores, the sequence of the molecule can be read off as often as desired by flossing, yielding infinite-depth sequencing at the level of an individual molecule. This approach may lead to successful characterization of native, unamplified DNA molecules with rare epigenetic modifications or native, low in abundance RNA molecules that frequently carry biologically significant modifications that are normally lost in ensemble averaging. Finally, we strongly believe that our double nanopore approach may, at last, realistically provide a way to use solid-state nanopores as a superior and scalable technique for high-throughput, direct and long-read nanopore sequencing of individual DNA and RNA molecules.

There are, of course, several technical difficulties that must be overcome for practical implementation of such infinite depth sequencing. One is device fabrication, which, in addition to sculpturing the delivery channels and the reader nanopores, will need to incorporate surface coating to prevent DNA sticking to the device surfaces.⁵⁴ Another is developing approaches to handle biomedically relevant fragments of ssDNA and ssRNA molecules, which could involve hybridization to dsDNA handles. We also note that while a dual-reader double nanopore system can provide bumper-to-bumper DNA or RNA sequencing, it should also be possible to use our nanofluidic double nanopore setup with a single reading nanopore, where the latter could either be a nanopore in a 2D material or a biological nanopore incorporated in a lipid bilayer membrane.⁵⁵

METHODS

COMSOL software (COMSOL Multiphysics 5.3a) was used to obtain the distribution of the electrostatic potential and the fluid flow profiles. All simulations of ssDNA capture by the double nanopore system were performed using the Atomic Resolution Brownian Dynamics (ARBD) package.⁵⁶ The all-atom MD method⁵⁷ was combined with a steric exclusion model (SEM)⁵¹ to simulate infinite-depth sequencing of an ssDNA molecule.

Continuum modeling of electrostatics and solvent flow in a double nanopore system.

The COMSOL software package was used to generate continuum solutions to the electrostatics and hydrostatics problems on the computational domain subject to boundary conditions. The computational domain was a 330 × 190 × 400 nm³ rectangle, Fig. 1. It contained two identical delivery channels each connected through a nanopore to a common flow chamber. Each delivery channel had a rectangular cross section of 80 × 160 nm² at each end that linearly funneled down over a distance of 80 nm to a constriction, also 80 nm long, where the cross section was 25 × 50 nm². In the center of the constriction was an entrance to a cylindrical nanopore (10 nm in diameter and 10 nm in height), which extended from the delivery channel to the flow chamber. The two nanopores were separated by 170 nm. The walls between the two delivery channels were 10 nm thick, however this choice was made solely to keep the simulation volume small and is not critical for any of our results. The material properties of the interior of the system were set to those of water, i.e., 100 kg/m³ density, 0.00089 Pa·s dynamic viscosity, and relative permittivity of 80.

The flow velocity was obtained using the Laminar Flow module, which solves the equations

$$\rho (\overrightarrow{u}\cdot \overrightarrow{\nabla })\overrightarrow{u}=\overrightarrow{\nabla }\cdot \left(-\rho I+\mu \left(\overrightarrow{\nabla }\overrightarrow{u}+{(\overrightarrow{\nabla }\overrightarrow{u})}^T\right)\right)+\overrightarrow{F}$$

$$\rho \overrightarrow{\nabla }\cdot \overrightarrow{u}=0.$$

All fluid–solid interfaces were given a no-slip boundary condition whereas applied pressure was specified at the open boundaries at the inlets and outlets of the channels and the flow chamber. The distribution of the electrostatic potential was obtained using the Electrostatics module, which solves the equations

$$\overrightarrow{\nabla }\cdot \overrightarrow{D}={\rho }_v$$

$$\overrightarrow{E}=-\overrightarrow{\nabla }V.$$

The external potential was introduced into the calculation as a boundary condition for each fluid inlet and outlet. In this way, the boundary of each of the three electrolyte-filled channels could be set to a potential value of our choosing, generating a strong electric field in the nanopores that connected them.

We used a two step process to obtain the mesh upon which COMSOL solved the differential equations. First, a custom free tetrahedral mesh was created using a predefined ‘Extremely coarse’ element size everywhere in the computational domain except for the volumes occupied by the nanopores and the rectangular constrictions of the delivery channels, where the size parameter was set to ‘Extremely fine’. Additionally, the maximum element size was set to 0.8 nm in the nanopore volume. We used the resulting mesh to find the initial solution to the electrostatics and the fluid flow problems under the boundary conditions of the first nanopore capture. The solution was further refined using an adaptive mesh procedure with a maximum coarsening factor of 1 and an element growth rate of 2.5. The resulting mesh was then saved and used to solve all of the electrostatics and fluid flow problems for the coarse-grained simulations in this work.

Coarse-grained MD simulations of ssDNA capture and threading.

All simulations were performed using a GPU-accelerated simulation engine ARBD,⁵⁶ a 1 ps simulation time step, and a two-bead-per-nucleotide model of ssDNA that was developed to reproduce the equilibrium conformation and the force–extension properties of an unstructured DNA strand.⁵⁸ A Langevin integration scheme was used to maintain a constant temperature with damping coefficients of 42.25 and 41.37 Ų/ns for P and B beads, respectively. The coarse-grained MD simulation of ssDNA was coupled to the electrostatic potentials extracted from a continuum COMSOL model in the form of an external grid-based potential that applied to the backbone beads of the DNA. Each backbone bead was assigned an effective charge of 0.25e, where e is the charge of an electron, to account for charge screening in the nanopore systems.^59–61 Additionally, a repulsive steric potential was applied, in the form of a 3D grid potential, to prevent the DNA from penetrating the solid boundaries of the system, as well as the fluid inlets and outlets. The steric potential was generated using the find boundaries routine of the image processing Python module, scikit-image,⁶² to identify a set of boundary layers (in steps matching the 1 nm resolution of the grid) from the binary geometry data exported from COMSOL. The values of the steric potential were zero in the fluid channels and increased with each boundary layer n as kn², where k = 100 kcal/mol. Finally, ARBD was modified to include a description of hydrostatic forces exerted by the flow of solvent extracted from the COMSOL model, as $\lambda (\overrightarrow{u}-\overrightarrow{v})$, where $\overrightarrow{v}$ is the velocity of the particle, $\overrightarrow{u}$ is the velocity of the fluid, and λ is the Langevin damping coefficient of the beads. Note that this approach neglects the impact of the DNA on the fluid velocity.

Prior to capture simulations, a 1000-nt DNA strand was equilibrated in a 160 × 80 × 80 nm³ volume using a multi-resolution simulation protocol.⁶³ The dimensions of this volume were identical to those of the entry rectangular compartment of the first cross delivery channel, Fig. 1a. The initial conformation of the molecule was a 34 nm long straight line extending from the center of the volume along the x axis. The system was first simulated for 66 μs using a 10 ps time step with a resolution of 100 nt/bead. Following that the system was simulated for 500 ns using a 500 fs time step at 5 nt/bead resolution and then for another 500 ns simulations at 1 nt/bead resolution. One hundred DNA conformations were created in this manner and used to initiate 100 independent capture simulations.

All-atom MD simulations of ssDNA flossing.

The all-atom MD simulations were performed using NAMD2,⁶⁴ a 2 fs time step, periodic boundary conditions and particle mesh Ewald (PME) method to calculate the long range electrostatics.⁶⁵ Nosé-Hoover Langevin piston^66,67 and Langevin thermostat⁶⁸ were used to maintain constant pressure and constant temperature in the system. The CHARMM36 force field parameters⁶⁹ described the bonded and non-bonded interactions among, DNA, water and ions. The parameters for hexagonal boron nitride (hBN) were taken from Hilder et al.⁷⁰ A 8-10-12 Å cutoff scheme was used to calculate van der Waals and short range electrostatics forces. The vdW interactions between atoms of DNA, boron nitride, water, and ions were determined using the Lorentz–Berthelot mixing rules. SETTLE⁷¹ and RATTLE⁷² algorithms were applied to constrain bonds to hydrogen atoms in water and other covalent bonds, respectively. The system’s coordinates were saved every 4.8 ps. The analysis and post processing of the simulation trajectories were performed using VMD.⁷³

A six-layer, 16×7.8 nm² patch of hBN was created using the Nanotube Builder plugin of VMD. The distance between consecutive layers of the hBN membrane was set to 3.35 Å whereas the distance between the boron and nitrogen atoms within each layer was 1.45 Å. Atoms were removed from the hBN membrane to create a nanopore of a 1.5 nm diameter and the shape of the M1-NNN MspA constriction.⁹ Bonds within the hBN membrane were generated across the periodic boundaries using the Inorganic Builder plugin of VMD. A 28-nucleotide ssDNA strand of 5′-(TAC)₉T-3′ sequence was created using the NAB module of AMBERTOOLs.⁷⁴ Two nanopore systems were created by threading the same ssDNA molecule through the nanopore in two different global orientations: 3′-end or 5′-end first. Each system was then solvated in a box of TIP3P⁷⁵ water. Potassium and chloride ions were added to 2 M concentration using the Autoionize plugin of VMD. Each final assembled system measured 16 × 7.8 × 8 nm³ and contained approximately 92,000 atoms.

Following the assembly, the systems underwent 1200 steps of energy minimization using the conjugate gradient method to remove steric clashes. The systems were then equilibrated for 50 ns at a constant number of atoms, pressure (1 bar) and temperature (300 K), with harmonic restraints applied to the boron and nitride atoms. The restraints were applied relative to the initial coordinates of the atoms, the spring constants were 1 kcal/(mol Ų). During the equilibration, the water attained the expected density of 1g/cc while the DNA bases adhered to the hBN surface.

The production simulation of the double nanopore system was performed under the constant volume and temperature conditions using the multicopy algorithm of NAMD⁷⁶ and a custom tclForces script to exchange the forces on the DNA strands between the two simulations. The phosphorus atom at the 3′-end of the DNA in one system was connected to the oxygen atom of the 5′-end of the DNA in the other system using a harmonic spring potential, mimicking a configuration in which one continuous DNA extends through the flow chamber. The spring constant was chosen to be 1.43 kcal/(mol Ų) to match the experimental stretch modulus of ssDNA.⁷⁷ A voltage bias of 10 V was applied alternatively across the membrane of one or the other system to floss the DNA. The voltage bias was switched when the position of the reference atoms connected via the harmonic springs potential approached the boundary of the simulation system.