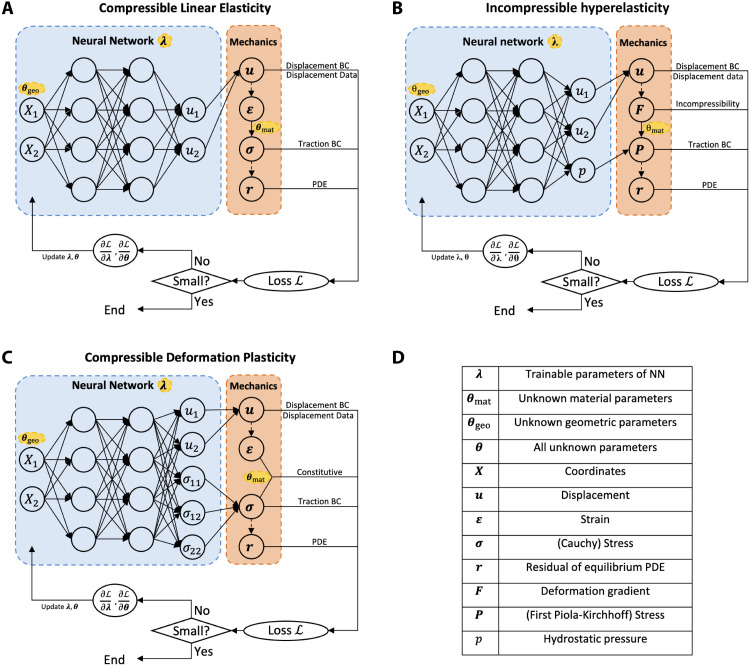
Fig. 3. Architectures of PINNs for continuum solid mechanics.

We established the PINNs for plane-strain problems involving geometry and material identification. Three material models are considered, including (A) compressible linear elasticity, (B) incompressible hyperelasticity, and (C) deformation plasticity. (A to C) We apply NNs with trainable parameters λ to approximate primary solution fields with respect to the in-plane coordinates (X₁, X₂). Mechanical laws are integrated to derive relevant mechanical quantities of interest from the NN outputs, such as strain, stress, and the residual of equilibrium PDEs, during which unknown material parameters θ_mat are involved. The loss function ℒ is formulated to represent the prediction error of each condition in the problem, such as PDEs, BCs, and data in (A), during which unknown geometric parameters θ_geo are involved because of the variable computational domain. Last, parameter estimation is conducted through the minimization of loss function. In this process, λ and θ = (θ_mat, θ_geo) are iteratively updated. The final solution of the identification problem is the updated value of θ after iterations. (D) Definitions of the notations in (A) to (C).