FIG. 6. Fractional testing.

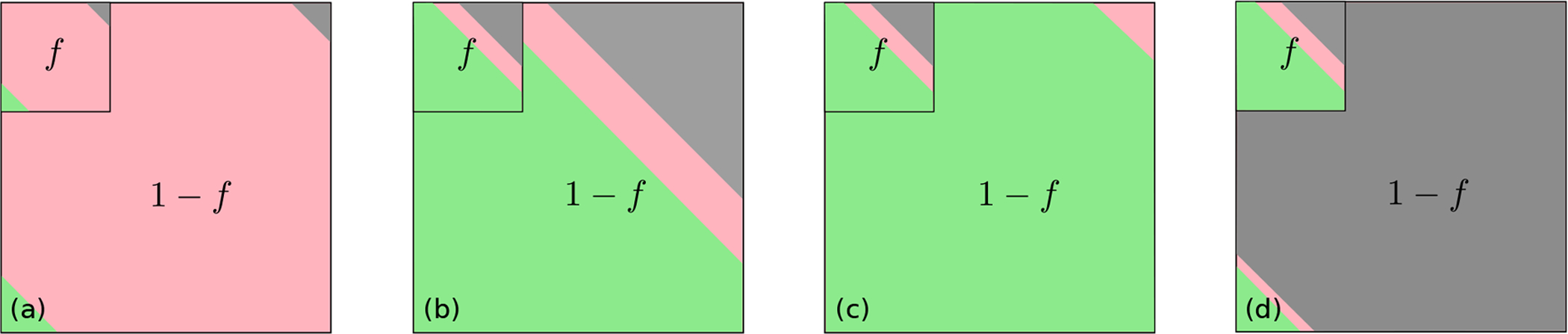
An example of fractional testing in which a fixed fraction f of the real total infected population is assumed to be tested. The remaining 1 − f proportion of infected individuals are untested. Equivalently, if the total tested fraction has unit population, then the fraction of the population that remains untested is 1/f − 1. (a) At short times after an outbreak, most of the infected patients, tested and untested, have not yet resolved (red). Only a small number have died (gray) or have recovered (green). (b) At later times, if the untested population dies at the same rate as the tested population, M_p(t) and CFR remain accurate estimates for the entire infected population. (c) If the untested population is, say, asymptomatic and rarely dies, the true mortality ${\mathcal{M}}_{\text{p}}^{0,1}(\infty )\approx f{M}_{\text{p}}^{0,1}(\infty )$ can be significantly overestimated by the tested mortality $M_{\text{p}}^{0,1}(t)$. (d) Finally, in a scenario in which untested infected individuals die at a higher rate than tested ones, $M_{\text{p}}^{0,1}(t)$ and CFR based on the tested fraction underestimate the true mortality ${\mathcal{M}}_{\text{p}}^{0,1}$.