Figure 2.

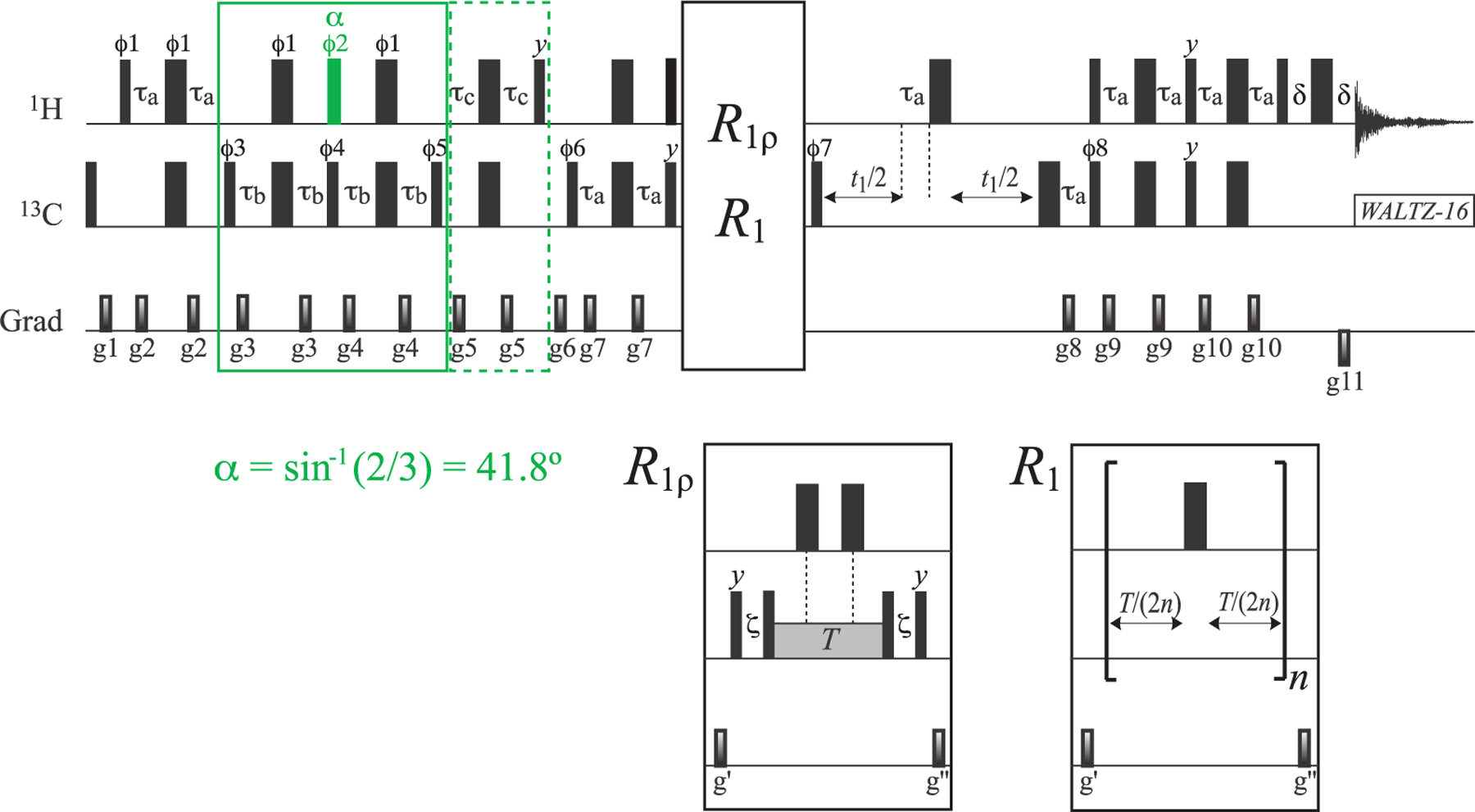
Pulse scheme for the measurement of R_1ρ and R₁ relaxation rates of the ¹³C magnetization mode (L₅ + L₆) (I = 1/2 manifold) in ¹³CH₃ methyl groups. All narrow and wide rectangular pulses are applied with flip angles of 90° and 180°, respectively, along the x-axis unless indicated otherwise. For ILV-{¹³CH₃}-labeled samples, the ¹H and ¹³C carrier frequencies are positioned at 0.5 and 20 ppm, respectively, in the center of the Ileδ1-Leu-Val methyl region; for Iδ1-{¹³CH₃}-labeled samples, the ¹H and ¹³C carrier frequencies are set to 0.7 and 12 ppm, respectively. All ¹H and ¹³C pulses are applied with the highest possible power, while ¹³C WALTZ-16 decoupling²³ is achieved using a 2 kHz field. The ¹H pulse colored in green is applied with flip angle α equal to sin⁻¹(2/3) = 41.8°. Delays are τ_a = 1/(4J_HC) = 2.0 ms; τ_b = 1/(8J_HC) = 1.0 ms; τ_c = 1/(12J_HC) = 0.67 ms; δ = 300 μs; and ζ = 1/(2π × B_SL) – (4/π) × pwc,^24,25 where B_SL is the strength of ¹³C spin-lock field (Hz) applied along the x-axis, “pwc” is the length of the ¹³C 90° (high power) pulse. T is a variable relaxation delay. The durations and strengths of the pulsed-field gradients (ms; G/cm) are as follows: g1 = (1; 25), g2 = (0.4; 15), g3 = (0.3; 12), g4 = (0.35; 15), g5 = (0.2; 20), g6 = (1.2; −15), g7 = (0.4; 12), g8 = (0.2; 35), g9 = (0.5; 12), g10 = (0.4; 12), g11= (0.053; −35), g′= (1.2; 12), and g″= (0.8; 10). The phase cycle is as follows: ϕ1 = x; ϕ2 = 2(y), 2(−y); ϕ3 = 2(x), 2(−x); ϕ4 = y, −y; ϕ5 = 4(x), 4(−x); ϕ6 = 2(x), 2(−x); ϕ7 = x, −x; ϕ8 = x; receiver phase = 2(x, −x), 2(−x, x). Quadrature detection in t₁ is achieved in a Rance-Kay mode^26,27 by recording a pair of data sets for each value of t₁ corresponding to (ϕ8, g8) and (−ϕ8, −g8). The phase ϕ7 is incremented by 180° along with the phase of the receiver for each complex t₁ point.²⁸