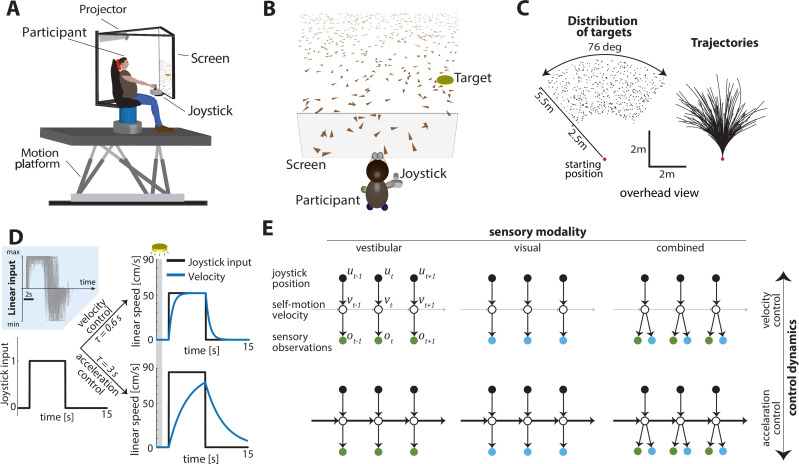
Figure 1. Experimental design.

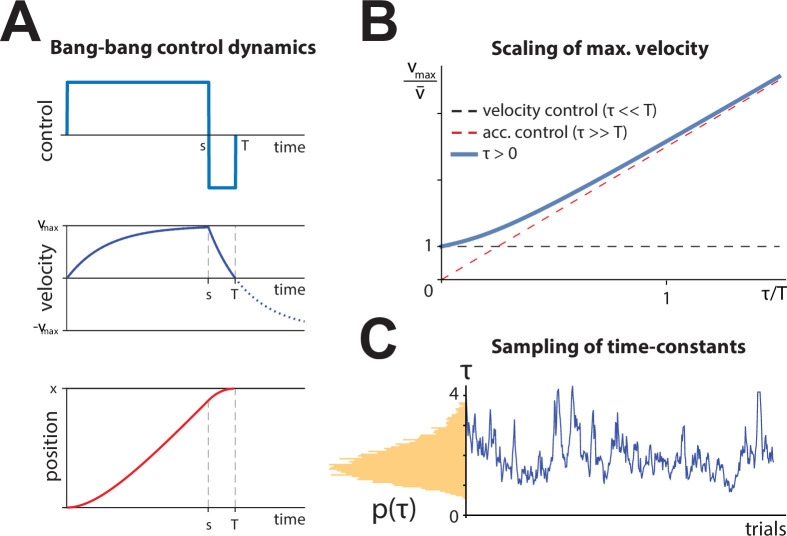
(A) Experimental setup. Participants sit on a six-degrees-of-freedom motion platform with a coupled rotator that allowed unlimited yaw displacements. Visual stimuli were back-projected on a screen (see Materials and methods). The joystick participants used to navigate in the virtual world is mounted in front of the participants’ midline. (B) Schematic view of the experimental virtual environment. Participants use a joystick to navigate to a cued target (yellow disc) using optic-flow cues generated by ground plane elements (brown triangles; visual and combined conditions only). The ground plane elements appeared transiently at random orientations to ensure they cannot serve as spatial or angular landmarks. (C) Left: Overhead view of the spatial distribution of target positions across trials. Red dot shows the starting position of the participant. Positions were uniformly distributed within the participant’s field of view. Right: Movement trajectories of one participant during a representative subset of trials. Starting location is denoted by the red dot. (D) Control dynamics. Inset: Linear joystick input from a subset of trials in the visual condition of an example participant. Left: Simulated maximum pulse joystick input (max joystick input = 1) (see also Figure 1—figure supplement 3). This input is lowpass filtered to mimic the existence of inertia. The time constant of the filter varies across trials (time constant τ). In our framework, maximum velocity also varies according to the time constant τ of each trial to ensure comparable travel times across trials (see Materials and methods – Control Dynamics). Right: The same joystick input (scaled by the corresponding maximum velocity for each τ) produces different velocity profiles for different time constants (τ = 0.6 s corresponds to velocity control; τ = 3 s corresponds to acceleration control; τ values varied randomly along a continuum across trials, see Materials and methods). Also depicted is the brief cueing period of the target at the beginning of the trial (gray zone, 1 s long). (E) Markov decision process governing self-motion sensation (Materials and methods – Equation 1a). $u$, $v$, and $o$ denote joystick input, movement velocity, and sensory observations, respectively, and subscripts denote time indices. Note that due to the 2D nature of the task, these variables are all vector-valued, but we depict them as scalars for the purpose of illustration. By varying the time constant, we manipulated the control dynamics (i.e., the degree to which the current velocity carried over to the future, indicated by the thickness of the horizontal lines) along a continuum such that the joystick position primarily determined either the participant’s velocity (top; thin lines) or acceleration (bottom; thick lines) (compare with (D) top and bottom, respectively). Sensory observations were available in the form of vestibular (left), optic flow (middle), or both (right).

Figure 1—figure supplement 1. Motion Cueing framework.

(A) Flow diagram of motion-cueing (MC) algorithm.

The participant pilots themselves in a simulated environment using a joystick. The MC algorithm aims at controlling a platform such that the sum of inertial and gravitational acceleration experienced when sitting on the platform (desired platform gravito-inertial acceleration [GIA], blue; the curve illustrates an example profile consisting of a single rectangular waveform) matches the linear acceleration experienced in the simulated virtual environment. ‘Desired’ refers to the fact that the motion platform may not be able to match this acceleration exactly. The desired GIA is fed through a step impulse function to compute the desired linear acceleration of the platform. The difference between the desired linear acceleration and GIA is used to compute the desired platform tilt. The desired platform motion (linear and tilt motion) are passed through a controller that restricts its motion to the actuator’s limits (in terms of linear and angular acceleration, velocity, and position). The two actuator output commands are sent to the platform and are also used to compute the actuator GIA which is actually rendered by the platform. To ensure that the inertial motion produced by the platform matches the motion in the simulated environment, the actuator GIA is compared to the desired linear acceleration to compute an actuator GIA error feedback signal, which updates the simulated motion. (B) Acceleration profile of an actual trial. The first panel shows the desired GIA of the participant for that trial. The second and third panels show the desired linear acceleration (red) and desired tilt acceleration (green), respectively. The fourth panel shows the final GIA achieved (blue) and the GIA error (magenta). (C) Correspondence between visual acceleration and platform GIA (blue), measured independently from the MC algorithm using an inertial measurement unit mounted next to the participant’s head. There is an almost perfect match between the two. The gray histogram indicates the range of acceleration experienced by the participant.

Figure 1—figure supplement 2. Verification of Motion Cueing output.

(A) Net gravito-inertial acceleration (GIA; thick lines) and net GIA error (thin lines) aligned to start and end of trial, for the vestibular and combined conditions across participants (average across trials over all time constants).

The dashed line represents a conservative choice of the vestibular motion detection threshold according to the relevant literature (8 cm/s²; Kingma, 2005; MacNeilage et al., 2010; Zupan and Merfeld, 2008). Gray region represents the target presentation period. Shaded regions denote ±1 SEM. (B) Net tilt velocity aligned to start and end of trial, for the vestibular and combined conditions across participants. Dashed line represents the estimated tilt/translation discrimination threshold of 1 deg/s: although tilt/translation discrimination thresholds have not been explicitly studied, we can use the rotation sensation thresholds of the semicircular canals to estimate what that threshold would be. Since it is the rotation velocity that tells a participant that they are tilting and not translating, we propose that the tilt/translation discrimination threshold is at least the same as the rotation sensation threshold (if not larger; Lim et al., 2017; MacNeilage et al., 2010). Shaded regions represent ±1 SEM across participants. Inset shows the probability distribution of displacements during the suprathreshold tilt period after trial onset (~0.6 s). Although the tilt can be perceived by the participants during trial onset, the displacement during that period does not exceed 10 cm and could potentially not contribute significantly to steering errors, for three reasons: (a) the displacement during that period is negligible, (b) tilt velocity is kept below the perceptual threshold for the remainder of the trajectory, (c) GIA is always above the motion detection threshold of the vestibular system. However, since the initial tilt could be perceived (as it briefly exceeded the canal detection threshold), this might alter the perceived orientation of the participants. In turn, this could influence the extent to which vestibular cues would be used as input to the path integration system (see Discussion ‘Limitations and future directions’ for further discussion). Thus, perceived tilt might be used as an indicator of trial onset, but it cannot contribute to path integration for three reasons: (a) the displacement during that period is negligible, (b) tilt velocity is kept below the perceptual threshold for the remainder of the trajectory, (c) GIA is always above the motion detection threshold of the vestibular system.

Figure 1—figure supplement 3. Control dynamics framework.

(A) Example dynamics for bang-bang control.

Position, velocity, and controls are shown. Control switches at time s and ends at time T. (B) Maximal velocity (blue) needed for bang-bang control to produce a desired average velocity ${\displaystyle \overline{u}=x/T}$ , as a function of the fraction of trial duration given by the time constant, $\tau /T$ . When the time constant is a small fraction of the trial (velocity control), the max velocity equals the average velocity (orange line). When the time constant is much longer than a trial (acceleration control), the maximum velocity grows as $4\tau /T$ (green), although this speed is never approached since braking begins before the velocity approaches equilibrium. (C) Example dynamics for control behavior. Left: Log-normal distribution of control time constants $\tau$ (see also Figure 3—figure supplement 1A). Right: Example random walk in $\log \tau$ space.