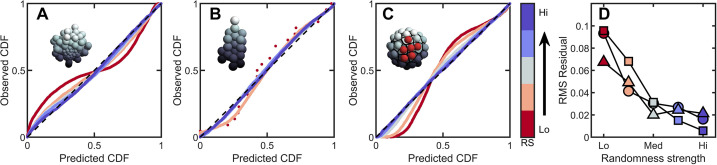
Figure 4. Introducing correlations and structure can break the maximum entropy distribution.

In A-C are PP plots of the observed vs. predicted cumulative distribution function for three different simulations. The colors correspond to increasing levels of noisiness in the simulations, from red (strongest correlations/determinism) to blue (strongest noise). The dashed black line in each represents $y=x$, or exact predictive efficacy. (A) Aggregative groups with bimodal size polydispersity; noise is introduced by varying the probability that small cells reproduce into small or large cells, and vice versa. (B) Tree-like groups with persistent intercellular bonds that grow according to a growth plan modified by noise in cell placement. (C) Surface-bound groups with programmed cell death events that may be localized or randomly dispersed. (D) The root mean square deviation from predicted values for each simulation case. Circles are aggregative simulations from A, triangles are tree-like simulations from B, and squares are surface-bound simulations from C. Note: the discrete points in (B) arise because absent randomness in the cell locations the exact same cellular structure is achieved by every simulation. Therefore, the observed distribution of Voronoi volumes is noticeably discrete for this case. Upon adding randomness, the cellular structure is altered between successive simulations, and the distribution of Voronoi volumes becomes less discrete.