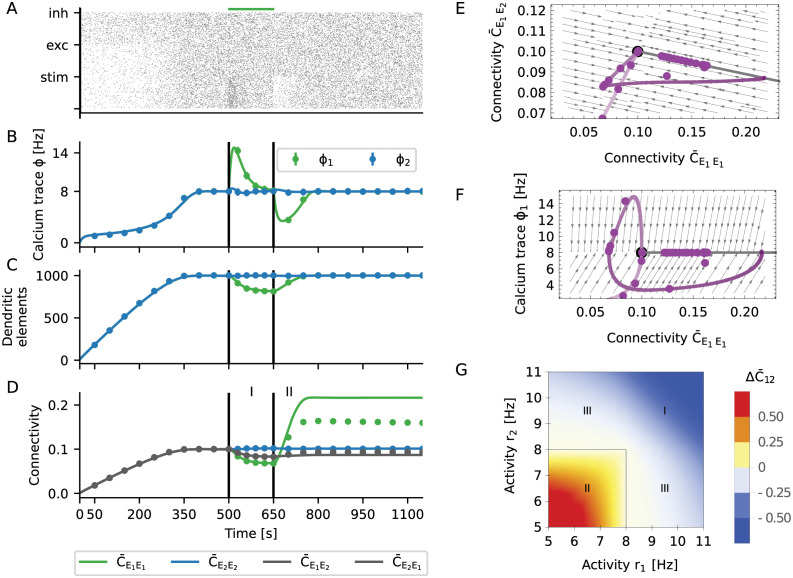
Fig 4. Hebbian properties emerge through the interaction of selective input and homeostatic control.

(A) The activity of the neuronal network was subject to homeostatic control. For increased external input, it transiently responded with a higher firing rate. With a certain delay, the rate was down-regulated to the imposed set-point. When the stimulus was turned off, the network transiently responded with a lower firing rate, which was eventually up-regulated to the set-point again. The activity was generally characterized by irregular and asynchronous spike trains. (B) It was assumed that the intracellular calcium concentration followed the spiking dynamics, according to a first-order low-pass characteristic. Dots correspond to numerical simulations of the system, and solid lines reflect theoretical predictions from a mean-field model of dynamic network remodeling. (C) Dendritic elements (building blocks of synapses) were generated until an in-degree of K_in = 1000 was reached. This number slightly decreased during specific stimulation, but then recovered after the stimulus was removed. (D) Synaptic connectivity closely followed the dynamics of dendritic elements until the recovery phase, when the recurrent connectivity within the stimulated group E₁ overshooted. (A–D) Black vertical lines indicate beginning and end of the stimulation. (E, F) Phase space representation of the activity. The purple lines are projections of the full, high-dimensional dynamics to different two-dimensional subspaces: (E) within-engram connectivity vs. across-ensemble connectivity and (F) within-engram connectivity vs. engram calcium trace. The dynamic flow was represented by the gray arrows. The steady state of the plastic network was characterized by a line attractor (thick gray line), defined by a fixed total in-degree and out-degree. The ensemble of stimulated neurons formed a stable engram, and the strength of the engram was encoded by its position on the line attractor. (G) The effective “instantaneous” learning rule for the expected connectivity between a pair of neurons is homeostatic in nature. It could also be viewed as an “inverse covariance rule” with baseline at the set-point of the homeostatic controller. The emerging Hebbian properties results from the more long-term combinatorial properties of rewiring across the whole network.