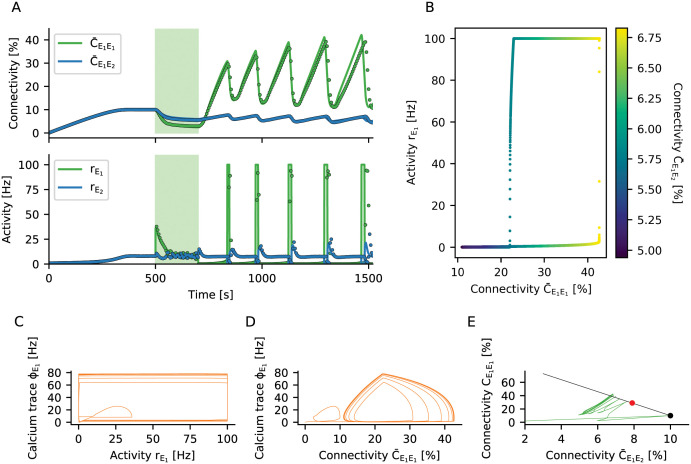
Fig 7. Non-linear stability of a network with homeostatic structural plasticity.
(A) The engram E1 is stimulated with a very strong external input. As the homeostatic response triggers excessive pruning of recurrent connections, the population E1 is completely silenced after the stimulus is turned off. This, in turn, initiates a strong compensatory overshoot of connectivity and consecutive runaway population activity. The dots with corresponding color show the results of a plastic network simulation, and the solid lines indicate the corresponding predictions from our theory. The theoretical instantaneous firing rate is clipped at 100 Hz. (B) The network settles in a limit cycle of connectivity dynamics. The hysteresis-like behavior is caused by the faster growth of within-engram connectivity as compared to connectivity from the non-engram ensemble . During the initial phase of the cycle, the increase of has no effect on the activity of population E1 yet, as its neurons are not active. Only when the input from population E2 through gets large enough, the rate becomes non-zero and rises to very high values quickly due to already large recurrent connectivity. (C) The calcium signal ϕ adds an additional delay to the cycle. (D) This leads to smoother trajectories when scattering calcium concentration against connectivity. (E) Connectivity within the stimulated group plotted against input connectivity from the non-engram population . The black line shows configurations with constant in-degree, of which the black dot represents the most entropic one. The red dot corresponds to critical connectivity, beyond which the limit cycle behavior is triggered. The limit cycle transients in connectivity space are orthogonal to the line attractor, indicating that the total in-degree is oscillating and no homeostatic equilibrium can be established.