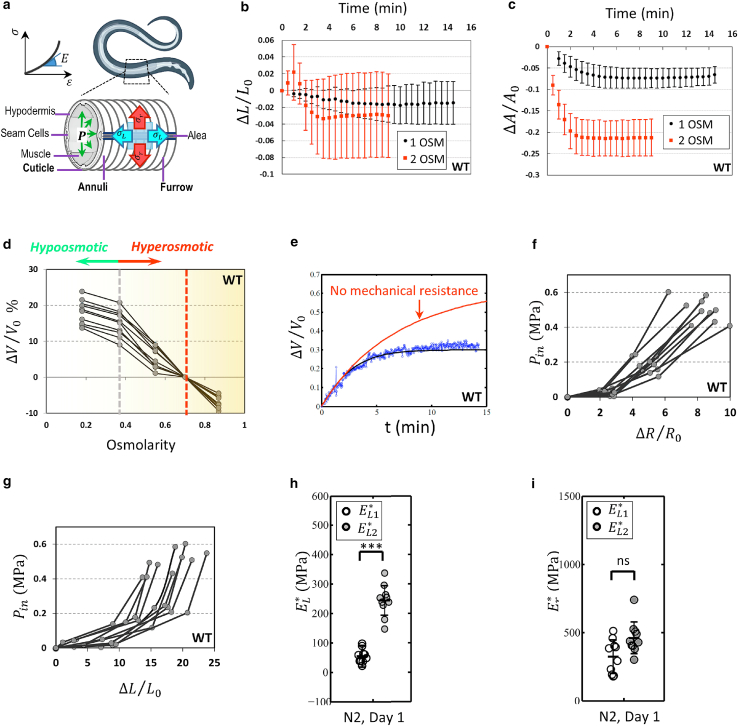
Figure 1.

Anisotropic and nonlinear elasticity of C. elegans. (a) Internal pressure stretches C. elegans' cuticular structures (annuli, furrow, and alae). (b and c) Time course measurement of worms' length and projected area after transfer to high osmolarity solutions. Higher osmolarity solutions generate more overall shrinkage and it may take up to 20 min for water exchange to reach the steady state. n = 10 per condition. (d) Wild-type animals were transferred from hyperosmotic medium to hypoosmotic medium quasi-statically. $V_0$ is the volume of the flaccid worms. n = 10 per condition. (e) Time course measurement of volume upon transferring worms to lower osmolarity solution (0.55 to 0.25 OSM). Applying a mathematical model to these data points, we can estimate the mechanical force resisting swelling. $V_0$ is the initial volume of the animal before the osmotic shock. (f and g) Using our mathematical model and body shape change data, the internal pressure can be calculated. n = 10 per condition. Elastic moduli in radial (h) and longitudinal (i) directions for wild-type worms under small and large stretching loads. Wild-type animals have no osmotic resistance phenotype. n = 10 per condition; two biological replicates. Two-tailed t-tests. ^∗∗∗p < 0.001. Plots show 25th percentile, median, and 75th percentile. To see this figure in color, go online.