FIG. 18.

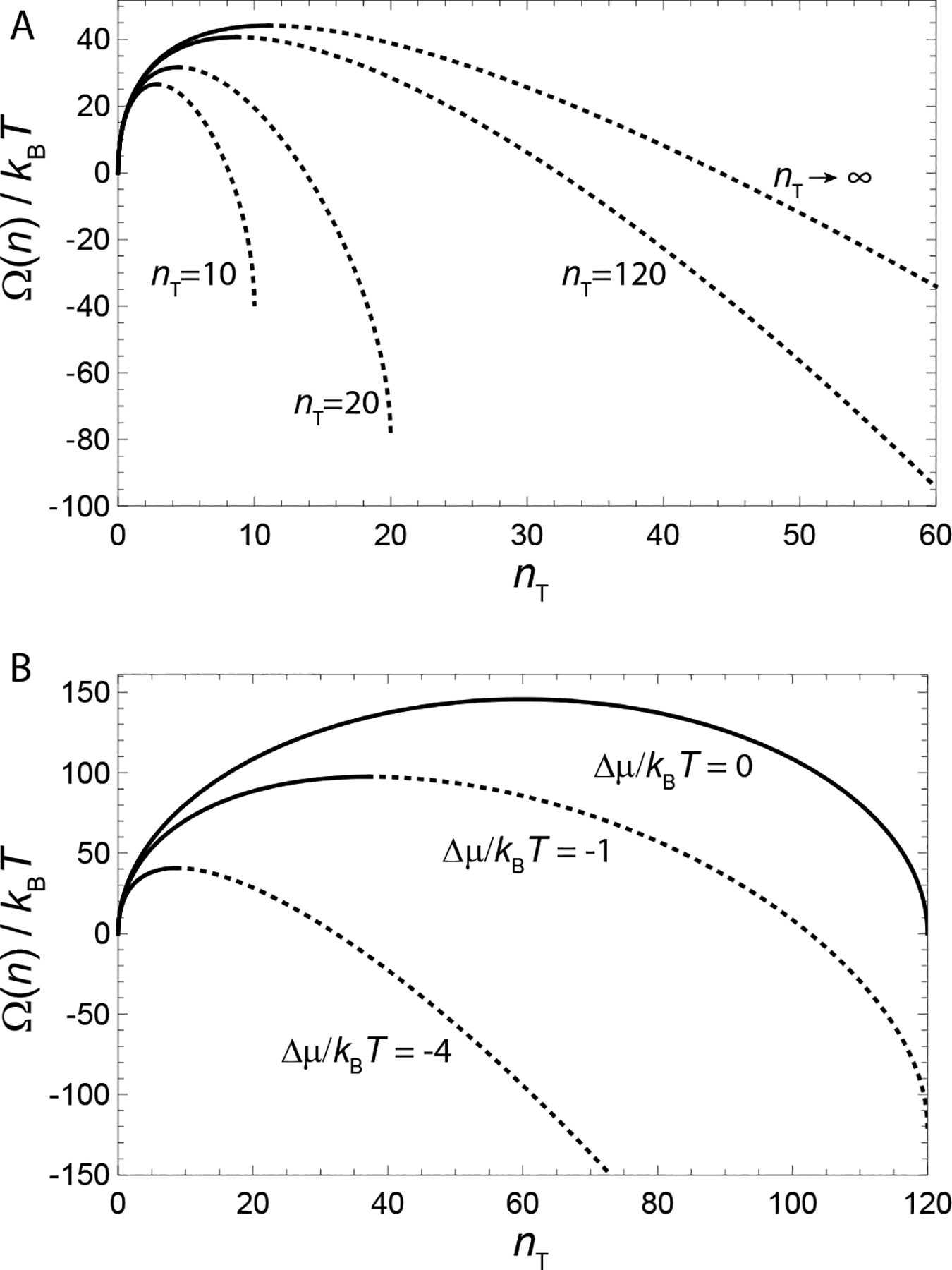
The grand free energy Ω for the capsid model with fixed curvature R_T (Eq. (70)), as a function of partial capsid size n. (A) shows Ω(n) for indicated complete capsid sizes n_T, with the limit n_T → ∞ corresponding to unlimited assembly (a flat disk). The calculation is performed for a chemical potential difference Δμ = −ϵ_T − μ = −4k_BT, and a per-subunit binding free energy ϵ_T = −15k_BT, corresponding to a subunit-subunit contact energy of 7.5k_BT and tetravalent subunits (e.g. (Ceres and Zlotnick, 2002b; Zlotnick et al., 2000)). We set the line energy to $\lambda ={ϵ}_{\text{T}}/2a_0^{1/2}$, corresponding to one unsatisfied contact per subunit on the partial shell rim. (B) shows Ω(n) as a function of the chemical potential difference Δμ for ϵ_T = −15k_BT and complete capsid size n_T = 120. In (A) and (B), the solid lines correspond to sizes for which the quasi-equilibrium approximation described in the text applies (i.e., n ≤ n_nuc) and thus the concentration of intermediates is approximately given by ϕ(n) ∝ e^−βΩ(n). The dashed lines correspond to sizes n > n_nuc for which this assumption is not valid and the intermediate concentrations cannot be described by a quasi-equilibrium (except approximately for the case Δμ = 0).