FIG. 7.

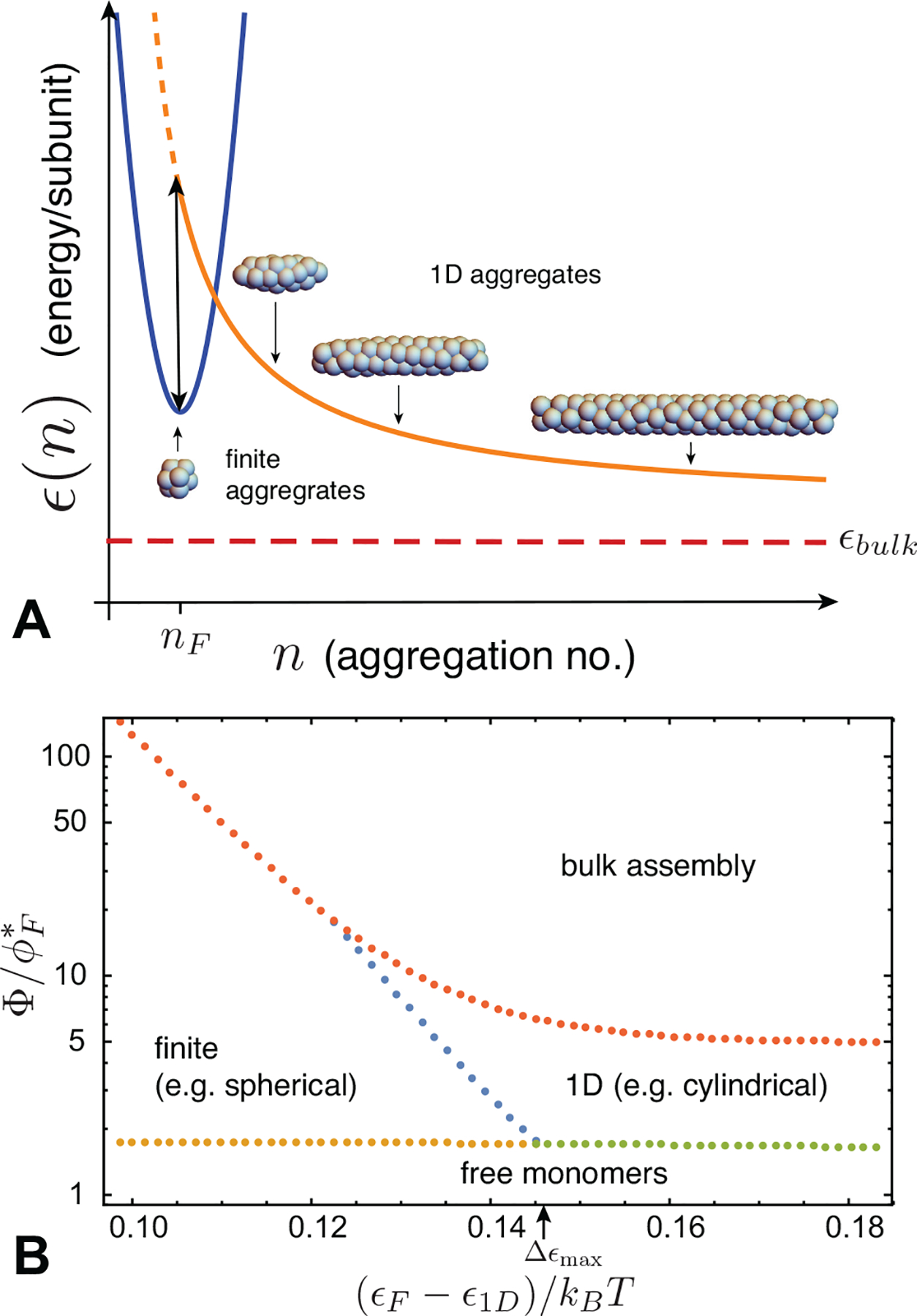
(A) A schematic plot of polymorphic aggregation energetics with three competing branches of assembly: finite aggregates (blue) with a local minimum at n_F, 1D aggregates (orange), and bulk aggregates (n → ∞ energy shown as red dashed line). In this case, the infinite 1D aggregate has a lower per subunit energy than finite aggregates, and there is a barrier (in total energy) δ that separates these states at n = n_F, i.e. the double arrow in (A) corresponds to δ/n_F. (B) Phase diagram for concentration-dependent size selection. The dominant aggregation state is shown for a system with coexistence among finite aggregates with n_F = 100 subunits, separated by an energy gap ϵ_F − ϵ_1D and a barrier of δ, eq. (34), to 1D aggregates. There is an additional per subunit energy gap of ϵ_1D − ϵ_bulk = 0.0005k_BT between 1D and bulk aggregates. The horizontal axis gives the energy gap between spheres and cylinders, and the vertical axis gives the total concentration relative to the CAC for finite aggregates ${\varphi }_{\text{F}}^{*}\simeq e^{\beta {ϵ}_{\text{F}}/n_{\text{F}}}$. The boundaries between monomers, finite and 1D aggregates are determined by crossovers in the most populous aggregate type from eq. (30), while the point of bulk saturation is determined by the point when μ = ϵ_bulk. In this example, the energy per subunit in finite aggregates is fixed at ϵ_F = −10 k_BT and the endcap energy of spherocylinders is Δ₀ = 20 k_BT. The maximum energy gap for which 2nd CAC behavior occurs (Δϵ_max ≈ 0.14 k_BT, eq. 35) is indicated on the x-axis.