Do aggregate, multimodal structural neuroimaging measures replicate regional developmental differences observed in highly cited cellular histological studies?

Abstract

Influential investigations of postmortem human brain tissue showed regional differences in tissue properties at early phases of development, such as between prefrontal and primary sensory cortical regions. Large-scale neuroimaging studies enable characterization of age-related trajectories with much denser sampling of cortical regions, assessment ages, and demographic variables than postmortem tissue analyses, but no single imaging measure perfectly captures what is measured with histology. Using publicly available data from the Pediatric Imaging, Neurocognition, and Genetics (PING) study, including 951 participants with ages ranging from 3 to 21 years, we characterized cortical regional variability in developmental trajectories of multimodal brain imaging measures. Multivariate analyses integrated morphometric and microstructural cortical surface measures. To replicate foundational histological work showing delayed synapse elimination in middle frontal gyrus relative to primary sensory areas, we tested whether developmental trajectories differ between prefrontal and visual or auditory cortex. We extended this to a whole-cortex analysis of interregional differences, producing cortical parcellations with maximally different developmental trajectories. Consistent with the general conclusions of postmortem analyses, our imaging results suggest that prefrontal regions show a protracted period of greater developmental change; however, they also illustrate the challenges of drawing conclusions about the relative maturational phases of different brain regions.

Highlights

• •Multimodal, multivariate, nonlinear modeling, integrating morphometric and microstructural measures.
• •Tested regional developmental differences previously found in highly influential cellular histological studies.
• •Produced cortical parcellations with maximally different, multimodal, developmental trajectories.
• •Findings converge with evidence from histological studies showing delayed prefrontal cortical development.
• •Interregional differences vary by measure and illustrate complexities of defining which regions mature first.

1. Introduction

Over the course of human development, from the embryo, into childhood, and through adolescence, the brain is constantly changing, engaged in maturational processes driven and shaped by factors related to genetics, environment, and experience. Foundational knowledge about these processes in humans has been gained through morphometric and histochemical studies of postmortem brain tissue (Huttenlocher, 1990, Huttenlocher and Dabholkar, 1997). Not simply a unitary phenomenon, brain maturation involves multiple processes, including dendritic and axonal growth, myelination, synaptogenesis, and synapse elimination, each with distinct developmental trajectories. Available evidence also indicates that the onset and time course of these processes vary substantially across the cortex (Barkovich, 1990, Becker et al., 1984, Schade and van Groenigen, 1961, Yakovlev and Lecours, 1967). Axonal growth and elongation begins in the fetus and continues through infancy (Haynes et al., 2005). The onset of myelination ranges from 20 to 24 post-conception (PC) weeks in the spinal cord and brainstem (Tanaka et al., 1995) to 25–37 PC weeks in the cerebrum (Hasegawa et al., 1992). The age at which myelin basic protein expression reaches “mature” levels also varies regionally, with estimates ranging from 34 PC weeks (Tanaka et al., 1995) to as late as 1 postnatal (PN) year (Haynes et al., 2005). Despite stabilization of protein expression patterns, myelination of subcortical white matter continues throughout childhood (Yakovlev and Lecours, 1967). Dendritic elongation occurs primarily during the first few years of postnatal life, with dendritic lengths reaching adult values earlier in visual and auditory cortex than in middle frontal gyrus (Becker et al., 1984, Huttenlocher and Dabholkar, 1997, Schade and van Groenigen, 1961). Synaptogenesis throughout the cerebral cortex begins in the fetus and exhibits a sharp increase within the first few years of postnatal life. Synapse elimination later leads to a gradual reduction in synaptic density, which reaches adult levels in late childhood or adolescence. In primary sensory areas such as visual and auditory cortex, peak synaptic density is achieved by age three months, with the reduction to adult levels complete around age 12 years. In contrast, a prefrontal cortical region, middle frontal gyrus, reaches peak synaptic density at about age 3.5, with adult levels not realized until age 16, according to limited postmortem human data (Huttenlocher, 1990, Huttenlocher and Dabholkar, 1997).

These types of morphometric and histochemical analyses in postmortem tissue are extremely valuable because they provide direct measures of tangible quantities such as dendritic length, synaptic density, and myelination, none of which can be obtained from noninvasive human brain imaging. Data of this type is relatively sparse, however, both in terms of the number of samples per study as well as the number of cortical regions that have been directly compared. For example, in his highly cited study of dendritic growth and synaptic density across age, Huttenlocher made measurements in just 13 individuals spanning the ages of 28 weeks gestational age to 71 years, comparing only striate cortex to frontal cortex (Huttenlocher, 1990). Medical conditions and causes of death are not detailed for these individuals, but the author states that samples may be affected by “agonal illness on the tissue and postmortem changes.” These limitations are due to the rarity of the postmortem samples in the immature brain, and perhaps also the painstaking nature of this type of work. These studies are also likely to include tissue from brains that may not be the most representative of typical development, since some involve clinical samples.

One reason for the lasting influence of these limited older studies continues to be the notable lack of more recent such empirical observations being made in human postmortem tissue across different ages during child development. For example, studies of synaptic density using several methods have been conducted in typically developing young and older adults, adults with neuropsychiatric illness, and adults with HIV and epilepsy (Alonso-Nanclares et al., 2008, Everall et al., 2006, Finnema et al., 2016, Hahn et al., 2009). One more recent study examined synaptic density in 42 subjects from 18 weeks gestation to 25 years and found early childhood increases in density through early childhood and decreases beginning in early adolescence, similar to Huttenlocher (Glantz et al., 2007). However, this study only made measurements in prefrontal cortex, so no inter-regional differences in developmental trajectories could be examined. Courchesne et al. examined postmortem neuron numbers and sizes in seven individuals with autism, compared with six typically developing children, all between two and 16 years old, but similarly made no comparisons with measures that were outside prefrontal cortex (Courchesne et al., 2011). Weir and colleagues characterized neural soma size, number of dendrites, and dendritic length in postmortem amygdala tissue from 16 typically developing individuals and 16 with autism aged seven to 44 years and modeled linear developmental increases for these morphological features (Weir et al., 2018).

Imaging-based morphometric and diffusion analyses have been increasingly used to probe the time course of maturational processes, albeit in a much more indirect way. It is assumed that maturational processes such as synapse elimination or myelination have effects on brain morphology and microstructure that are measurable using structural and diffusion magnetic resonance imaging (sMRI and dMRI, respectively), although our understanding of the linkage between specific imaging-derived measures and neurobiological variables like synaptic density or myelination is not direct, precise, or complete. For example, though fractional anisotropy (FA) is affected by myelination and is often used as an imaging marker of myelination, other factors, such as axon diameter, neurite density, or the presence of crossing fibers, also contribute to variation in FA. Each imaging-derived measure likely reflects a unique mixture of maturing neurobiological processes.

Changes observed in human imaging, such as the apparent progressive thinning of cortical gray matter or increases in FA of white matter are unlikely to reflect a single, unitary neurobiological mechanism of maturation, so the use of individual measures (e.g., cortical thickness, FA, T2-weighted signal intensity) likely provides an incomplete picture of the maturational processes in a given brain region. Indeed, when examined in isolation, the measures that can be derived from sMRI and dMRI for various subcortical and cortical regions of interest (ROIs) display variable rates of change over the course of development, with different measures and regions explaining the greatest variability in developmental phase at different periods of development (Brown et al., 2012, Fjell et al., 2012, Giedd and Rapoport, 2010, Mills et al., 2016, Tamnes et al., 2010, Walhovd et al., 2012, Westlye et al., 2010, Wierenga et al., 2018). For example, total cortical surface area increases during early childhood and then gradually declines throughout adolescence. In contrast, average cortical thickness monotonically decreases throughout both periods (Brown et al., 2012, Wierenga et al., 2014). In fact, even imaging measures that seem relatively straightforward to interpret and relate to the underlying neurobiology, such as cortical thickness, have been shown to be highly inconsistent and unreliable in their purported developmental trajectories, underscoring the need to continue to validate findings from imaging with other non-imaging neuroscientific measures and methods (Walhovd et al., 2016). Diffusion-derived measures in long-range white matter tracts also undergo great changes during this time, with FA generally increasing and mean diffusivity (MD) generally decreasing with age (Barkovich, 1990, Dubois et al., 2014, Lebel and Deoni, 2018, Lebel et al., 2019, Salamon, 1990, Wolpar and Barnes, 1992). In contrast to the long-range white matter tracts, less is known about the developmental changes in the short-range U-fibers that underlie cortical gray matter, often referred to as pericortical white matter. Differences among imaging-derived measures in the shapes of developmental trajectories within these areas presumably reflect the contributions of multiple maturational processes, such as myelination, dendritic arborization, and synaptic pruning. Studies that quantitatively aggregate across multiple imaging measures, thereby capturing these different types of signals in the changing neurobiology, should provide a more complete metric of developmental differences and trajectories across different regions, allowing a fairer comparison with these classic, highly cited histological studies. Given how influential even these older studies still are in the field, it is important that their specific findings and interpretations be evaluated by modern means. For example, Huttenlocher and Dabholkar’s study from 1997 has been cited 3413 times since its original publication and was cited 197 times in 2021 (Google Scholar metrics),

Based on the relatively prolonged maturation of behavioral measures of executive functions through adolescence, and multiple lines and types of evidence showing the central role of prefrontal cortex in executive cognitive processes, prefrontal cortex is commonly thought to complete its development later than posterior cortical regions (Akshoomoff et al., 2018, Klenberg et al., 2001, Korkman et al., 2001, Korkman et al., 2013, Welsh et al., 1991, Willoughby et al., 2012). Direct, non-imaging evidence of delayed neuronal maturation in human prefrontal regions comes from the work of Huttenlocher and colleagues, who showed that onsets of both synaptogenesis and synapse elimination are delayed in specific areas of the middle frontal gyrus (MFG) relative to primary sensory areas visual and auditory cortex (Huttenlocher, 1990, Huttenlocher and Dabholkar, 1997). In light of this and other work, one would expect to find differences in the developmental trajectories of MRI-derived measures for these specific regions within prefrontal cortex relative to either primary visual or primary auditory cortex. Guided anatomically by these most direct available measures of human neuronal developmental differences, we wanted to use an aggregate collection of imaging measures derived from currently available modalities and types to examine the same areas within prefrontal and primary sensory cortex and test whether, with these measures, they exhibit different rates of maturation across early childhood. Specifically, we wanted to test whether prefrontal regions show delayed development relative to sensory areas, as was the primary interpretation of the histological studies, using the histological results and locations as the starting point for imaging comparisons. A major goal was to use these multiple sources of information about features and tissue properties to get past the limitations of plotting trajectories using only individual imaging measures, as the vast majority of previous studies have done. Such a comparison would serve as an informative, targeted validation of some of the most highly influential papers in developmental cognitive neuroscience, despite being based on such limited data sets. Comparisons in developmental trajectories guided by localized cellular results also might have greater neurobiological interpretive leverage than if locations were based on imaging studies alone. For example, developmentally accelerated apparent cortical gray matter thinning during adolescence in these regions may be driven at least in part by synapse elimination. In general, inter-regional differences in the shapes of the developmental trajectories of MRI-derived measures are likely to be manifestations of variation in the time course of maturational processes.

Certainly, some of the advantages of imaging studies over postmortem histological studies are the potential for much larger sample sizes, data from across the entire brain for comprehensive inter-regional comparisons, and the availability of spatially aligned cortical surface-based mapping approaches. Using publicly available data from the Pediatric Imaging, Neurocognition, and Genetics (PING) study, we implemented this approach and examined cortical, inter-regional variation in developmental trajectories of measures derived from multimodal brain imaging (Jernigan et al., 2016). These data were acquired from healthy children between the ages of 3 and 21, and developmental trajectories are inferred from cross-sectional analyses of the entire sample, controlling for key demographic variables. Measures derived from sMRI included cortical thickness, cortical surface area, sulcal depth, and T1-weighted signal intensity (T1w). Measures derived from dMRI included FA, MD, longitudinal diffusivity (LD), transverse diffusivity (TD), and T2-weighted signal (T2w), each sampled onto the cortical gray matter and pericortical white matter. Using this multimodal, multidimensional imaging approach, we established a test for aggregate variability across cortical regions in developmental trajectories. We tested main hypotheses derived from the well-known postmortem studies about maturational differences between specific regions (e.g., primary sensory cortex and middle frontal gyrus), and we produced new empirically derived whole-cortex maps of interregional similarity and difference based on the trajectories of development.

Maturational processes occurring at the cellular level in cerebral cortex, such as changes in synaptic or axonal density, are presumably reflected to varying degrees in the developmental trajectories of imaging-derived measures related to cortical morphology and microstructure. An examination of regional variability of these putative maturational biomarkers, using several available imaging measures altogether instead of just one, could reveal whether some cortical regions reach a relatively mature aggregate state at an earlier age, such as in early adolescence, while others such as prefrontal cortex continue to mature into adulthood, as is commonly believed. The ability to examine developmental trajectories as multimodal statistical aggregates may help to get around the limitations of using only individual imaging measures in seeking to verify cell-level developmental differences, as most previous imaging studies have done. If prefrontal cortex matures relatively late, as the prolonged maturation of executive functions in adolescence strongly suggests and as a handful of human histochemical studies suggest, measures of prefrontal tissue properties from multimodal neuroimaging should support this contention, as compared to other brain regions.

2. Materials and methods

2.1. PING data repository

Data used for this study were obtained from the PING repository (https://www.nitrc.org/projects/ping), a publicly shared data resource comprising standardized assessments of behavioral, neuroimaging and genetic variables in typically developing children, adolescents and young adults (Jernigan et al., 2016). A code repository containing R and matlab code used in analyses described below has been made publicly available (https://github.com/djhagler/multivar-devel).

Data were collected at nine sites across the United States, with a total of 1493 participants with ages ranging from 3 to 21 years. Adult participants gave informed consent, and parental informed consent and subject assent, when appropriate, were obtained for participants under age 18. The human research protections programs and institutional review boards at participating institutions approved all experimental and consenting procedures. Participants were excluded based on medical conditions affecting development, including neurological disorders, head trauma, preterm birth (less than 36 weeks gestational age), severe psychiatric diagnosis (autism spectrum, schizophrenia, or bipolar disorders), mental retardation, or daily illicit drug use of the mother during pregnancy. Participants were also excluded if MRI was not indicated; for example, metallic or electronic implants, claustrophobia, or pregnancy. Complete sample characteristics and screening methods are described in Jernigan et al. (2016). Of the 1493 participants available in the PING repository, data from 951 were included in the currently described analyses (461 females, mean age = 12.0 years, SD = 4.9; ages 3–6: n = 112, ages 6–9: n = 179, ages 9–12: n = 206, ages 12–15: n = 156, ages 15–17: n = 148, ages 18–21: n = 150), after excluding participants lacking either sMRI or dMRI data (207 participants), that were unable to be fully processed1 (98 participants), that did not pass post-processing quality control for either modality (122 participants), or were lacking values used as covariates (115 participants without age, sex, socio-economic status, or genetic ancestry factors).

2.2. Imaging data acquisition

A standardized multimodal MRI data acquisition protocol was used on 12 different 3 T scanners (GE, Siemens, and Philips) across the 9 sites, details of which have been described previously (Jernigan et al., 2016). Briefly, imaging sessions included 3D T₁-weighted (T1w) and a high angular resolution diffusion imaging (HARDI) dMRI scan. Important features of the PING MRI protocol included prospective motion correction (PROMO) for structural scans (Brown et al., 2010, Kuperman et al., 2011, White et al., 2010), and calibration scans to map B0 distortion fields for dMRI scans (Holland et al., 2010). The sagittal T1w scans had voxel sizes of 1 × 1×1.2 mm. The axial 2D EPI dMRI scans had voxel sizes of 2.5 × 2.5 × 2.5 mm, a single b= 0 vol, and 30 (for GE and Siemens scanners) or 32 (for Philips scanners) diffusion gradient directions with b= 1000 s/mm². T1w and dMRI scans were collected for 1286 participants. Additional scans collected for most PING participants, but not used in the current study, were resting-state fMRI and 3D T2-weighted scans (n = 823 participants with fMRI and n = 970 with 3D T2-weighted).

2.3. Data processing

Image processing for the PING MRI dataset has been described previously (Jernigan et al., 2016). Standard processing and analysis steps relevant to the current study will be briefly summarized. Structural MRI preprocessing included gradient nonlinearity distortion correction (Jovicich et al., 2006), non-uniform intensity normalization (Sled et al., 1998), and resampling into alignment with an atlas brain with 1 mm isotropic voxels. Cortical surface reconstructions were created using FreeSurfer version 5.3.0 (Fischl, 2012), a process involving skull stripping (Segonne et al., 2004), non-uniformity correction (Sled et al., 1998), white matter segmentation, initial mesh creation (Dale et al., 1999), correction of topological defects (Segonne et al., 2007), and generation of optimal white and pial surfaces (Dale et al., 1999, Dale and Sereno, 1993, Fischl et al., 1999).

Measures extracted from the cortical surface reconstructions included cortical thickness (Dale et al., 2000), cortical area (Chen et al., 2012), and sulcal depth (Fischl et al., 1999). Cortical area was calculated from the white matter surface; i.e., the surface mesh reconstructing the boundary between cortical white and gray matter. Normalized T1w intensity values were derived from the “nu.mgz” volume produced by FreeSurfer, which is the result of non-uniformity correction and global normalization so that white matter intensity values are ~110, on a scale from 0 to 255. For convenience, intensity values were again normalized to range from 0 to 1 by dividing values by 255. The normalized T1w intensity values were resampled into the same voxel-space as the dMRI data and then sampled to the cortical surface as described below for dMRI-derived measures.

Diffusion MRI preprocessing included B0 distortion correction using the reversing gradient method (Holland et al., 2010), gradient nonlinearity distortion correction (Jovicich et al., 2006), eddy current distortion correction (Hagler et al., 2009, Zhuang et al., 2006), motion correction (Hagler et al., 2009), and resampling into rigid-body alignment with an atlas brain with 2 mm isotropic voxels (Hagler et al., 2009). Diffusion tensor imaging (DTI) methods were used to calculate measures related to microstructural tissue properties (Basser et al., 1994, Basser and Pierpaoli, 1996), including fractional anisotropy (FA), and mean, longitudinal, and transverse diffusivity (MD, LD, and TD). Rather than use the 3D T2-weighted images, which were collected in about 75% of the participants with T1w and dMRI scans, T2-weighted intensity (T2w) was calculated from the average of the dMRI b= 0 images. To account for intensity variation due to scanner gain settings, T2w images were normalized for each subject. The slope between MD and b= 0 intensity values, estimated using all brain voxels, was used to scale the T2w images (Jernigan et al., 2016), with an additional multiplication factor of 1000, resulting in brain voxel values around 1, with units of 10⁻³ mm²/s. DTI-derived measures were sampled onto the FreeSurfer-derived cortical surface mesh in order to make maps of diffusion properties for cortical gray matter and white matter adjacent to the cortex (Govindan et al., 2013, Kang et al., 2012). Values were sampled perpendicular to the gray/white boundary surface in 0.2 mm increments, ranging from 0.8 mm to 2 mm in both directions. White and gray matter values were calculated by combining samples within type using a weighted average based on the proportion of white or gray matter in each voxel (Elman et al., 2017). The same approach was used to sample T1w and T2w intensity values to the cortical surface, with T1w intensity volumes being first resampled into the same voxel-space as the DTI measures.

2.4. Quality control

Quality control (QC) procedures for the PING MRI dataset have been described in detail previously (Jernigan et al., 2016). Images were automatically checked for completeness and protocol compliance after upload to the PING Neuroimaging Core from the imaging sites. Within 24 h, unprocessed images were visually inspected and given quality ratings to indicate usability. T1-weighted images were examined for signs of excessive motion, such as severe ghosting, blurring, or ringing that would make accurate brain segmentation impossible. Diffusion-weighted images were examined for poor image quality or other artifacts (e.g., severe magnetic susceptibility artifact). dMRI acquisitions with five or more slices exhibiting significant motion-related artifacts (e.g., loss of signal) were rated as unacceptable. If imaging data were rated as unacceptable, subjects were rescanned if possible and excluded from further analysis if rescanning was not possible (n = 1294 participants with imaging data acquired, n = 1291 participants with acceptable T1w data, n = 1288 participants with acceptable dMRI data, n = 3 participants with no acceptable imaging data). Processed imaging data were also reviewed for each participant, including subcortical volumetric segmentations, cortical areal parcellations, and white and pial surface reconstructions. Each segmentation type was inspected and rated as acceptable or not. DTI-derived FA images were reviewed for accuracy of registration to the T1w volume and image quality issues (e.g., high noise, motion artifacts, warping, etc.). No manual interventions, such as editing of white matter segmentation or manual registration of DTI to T1w, were performed. Only participants with acceptable cortical surface reconstructions (n = 1252 of 1290, or 97%) and DTI results (n = 1093 of 1187 fully processed, or 92%) were included in the current analyses (see Supp. Fig. 1 for a flow-chart depiction of QC-related exclusions).

2.5. Regions of interest analysis

We selected cortical regions that, based on the cellular histochemical work of Huttenlocher and colleagues, are predicted to exhibit large differences in the developmental trajectories of cortical maturation. Cortical regions of interest (ROIs) were specified using FreeSurfer’s atlas-based, cortical parcellation (Desikan et al., 2006; Fig. 1A). ROIs included primary visual cortex (pericalcarine) and primary auditory cortex (Heshl's gyrus), two sensory areas sampled in cellular studies and thought to mature early, as compared with middle frontal gyrus areas in the same studies. Because the standard FreeSurfer cortical parcellation includes caudal and rostral subdivisions of the middle frontal gyrus, and the cellular reported results without a coordinate system, we included both ROIs in separate analyses. For each ROI, we calculated averages of several cortical surface-based, neuroimaging measures derived from morphometric and microstructural analyses.

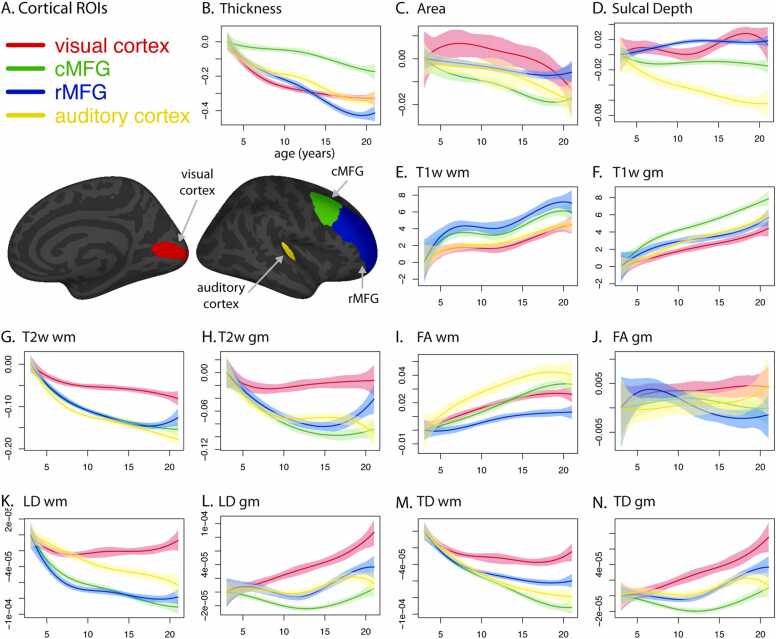
Fig. 1.

Developmental trajectories of imaging-derived measures in anatomically defined cortical regions. A. Selected cortical regions of interest are labeled on inflated surfaces of right hemisphere; medial view on left, lateral view on right. B - G. Spline fits and 95% confidence intervals for each ROI, plotted relative to values at age 3. B. cortical thickness (mm). C. area (mm² / vertex). D. sulcal depth (unitless). E. T1w in pericortical white matter (wm) (arbitrary units: AU). F. T1w in cortical gray matter (gm; AU). G. T2w wm (10⁻³ mm²/s). H. T2w gm (10⁻³ mm²/s). I. FA wm (unitless). J. FA gm (unitless). K. LD wm (mm²/s). L. LD gm (mm²/s). M. TD wm (mm²/s). N. TD gm (mm²/s). Sulcal depth and FA are unitless ratios that range from 0 to 1 by definition. T1w intensity values were normalized for each participant to remove scan-specific, whole brain intensity variation, resulting in arbitrary intensity units ranging from 0 to 1. T2w intensity values were normalized using a global fit between b= 0 intensities and MD values in the brain and multiplied by 1000, resulting in wm values around 1.

2.6. Univariate regressions

We used linear regression analyses to investigate differences in developmental trajectories between each pair of ROIs and between all pairs of points on the cortical surface. We calculated within-subject differences between locations for each of several sMRI- and dMRI-derived, cortical surface-based measures. Specific sMRI measures included cortical surface area, thickness, sulcal depth, and T1w sampled in both cortical gray and pericortical white matter. dMRI measures, sampled in gray and white matter, included FA, MD, LD, TD, and T2w.

Separately for each measure, we modeled quadratic functions of age for the pairwise differences between locations using the lm function (linear model) in R version 2.1.5 (Team, 2012). A likelihood ratio test was performed using the anova function (analysis of variance) in R to compare baseline vs. full models (Neyman and Pearson, 1933). The baseline model included scanner, sex, household income, parental education, and genetic ancestry factors (GAF) --genetically derived measures of ethnic ancestry (Jernigan et al., 2016). The full model included those baseline regressors plus age and age-squared, with age defined as age in years relative (by subtraction) to the minimum age of the sample (three years). F-statistics were reported as measures of the dissimilarity between the two cortical locations, for a given cortical measure, in the relationship with age expressed as a quadratic function.

The p-values reported in Supp. Tables 1, 2, 5, and 6 were corrected for multiple comparisons using the Bonferroni method (Bonferroni, 1936) in which the p-value is multiplied by the number of tests (set to 1 if greater than 1). Since we report p-values for both intercept and “trend” (age + age²), we corrected for the total number of tests in each set of inter-regional comparisons (i.e., 2 x number of ROI-ROI pairs x number of measures). With N = 951, the degrees of freedom for the F statistic of the full linear mixed effects models were 23 and 928.

2.7. Multivariate regression

Multivariate regression was used to test for differences in multimodal developmental trajectories between all pairs of ROIs and all pairs of points on the cortical surface. Multivariate regression allows for simultaneous estimation of the effects of independent variables on multiple outcome variables. Here, the multiple outcomes were the pairwise differences between each location's multimodal assessments (see Univariate Regressions). MD was excluded from the multivariate analysis because it is a linear combination of LD and TD. We tested nested multivariate regression models using the manova function (multivariate analysis of variance) in R. A likelihood ratio test was performed using the anova function in R to compare the two models. As with the univariate analyses described above, the baseline model included scanner, sex, household income, parental education, and GAF. The full model included these baseline regressors as well as age and age-squared (relative to age 3). The F-statistic associated with the Pillai's trace (Pillai, 1955) was reported as a measure of the dissimilarity between the two cortical locations in their multivariate relationship with age expressed as a quadratic function. The p-values reported in Table 3 and Supp. Table 7 were corrected for multiple comparisons using the Bonferroni method, with the number of tests equal to the number of ROI-ROI comparisons.

Table 3.

Multivariate statistics for the trend of inter-regional differences in imaging measures with respect to age and age squared for selected anatomically defined cortical regions. F-statistic associated with Pillai's trace from likelihood ratio test of MANOVAs (with 951 participants and 13 imaging measures). p-values corrected for multiple comparisons with Bonferroni method, with the number of tests equal to the number of ROI-ROI comparisons (i.e., 6).

ROI A	ROI B	F-statistic	p-value
VC	cMFG	23.9	2.7E-108
VC	rMFG	19.9	3.4E-90
VC	AC	19.0	1.3E-85
cMFG	rMFG	34.3	8.7E-153
cMFG	AC	12.9	3.1E-56
rMFG	AC	16.0	1.1E-71

2.8. Cortical parcellation with fuzzy clusters

Surface-based maps for each measure were sampled to the FreeSurfer atlas (Fischl et al., 1999) and smoothed along the cortical surface with a smoothing kernel equivalent to 40 mm full width half max (FWHM) (Hagler et al., 2006). The univariate and multivariate regression methods described above were then performed for each pair-wise combination of cortical surface vertices. To reduce the computational burden, surface maps were down-sampled (after smoothing) to a mesh with 2562 vertices per hemisphere (rather than 163842), resulting in ~7 mm spacing between vertices. For either a single measure or multiple measures, we computed F-statistics for the combined effect of age and age squared of the within-subject differences between each pair of points. The F-statistics were arranged into a square matrix with the number of rows equal to the number of vertices across both hemispheres, excluding vertices not labeled as cortex (4661). This forms a cortico-cortical “distance” matrix, representing either the univariate or multivariate dissimilarity in developmental trajectories. This distance matrix was used as input to a fuzzy clustering algorithm (Kaufman and Rousseeuw, 1990) – implemented in the fanny function in the R cluster package (Maechler et al., 2012) – that produced cluster membership scores for each vertex. Cluster membership scores were resampled back to the high-resolution mesh for display purposes, with 10 steps of sparse smoothing followed by 10 steps of conventional iterative smoothing. To determine the appropriate number of clusters, silhouette values were calculated after forming different numbers of fuzzy clusters, ranging from 2 to 10 clusters. Higher silhouette values are associated with greater differences between clusters than within clusters (Rousseeuw, 1987). An additional parameter of the fuzzy clustering algorithm, called the membership exponent (ME), determines the degree of overlap between clusters. ME values are required to be a number between 1 and 2. Sub-optimal values may prevent convergence of the algorithm for some numbers of clusters, so an array of values between 1 and 2 at 0.05 increments were tested; the ME value was chosen from those that provided solutions for each number of clusters between 2 and 10. For univariate clustering, ME was 1.25, and for multivariate clustering, ME was 1.2.

2.9. Smooth curve fitting

Imaging-derived measures, averaged within predefined ROIs or within the data-driven fuzzy cluster ROIs, were plotted as a smooth function of age. B-splines basis functions were used within the fda package of R (version 3.3.1) to smooth the ROI-averaged, imaging-derived measures across age (Ramsay et al., 2014). B-splines basis functions are piecewise-polynomial functions of bounded range, often used for smoothing non-periodic data. Each fit was comprised of four fifth-order B-splines. 95% confidence intervals were calculated through bootstrapping (1000 samples with replacement). Spline fits were calculated as a function of age, after regressing out covariates scanner, sex, household income, parental education, and GAF (Jernigan et al., 2016).

3. Results

3.1. Multimodal developmental trajectories in regions from histology studies

We visualized the cross-sectionally derived developmental trajectories (i.e., inferred trajectories) for each ROI and measure as a smooth function of age, using B-spline fits and bootstrap resampling to calculate 95% confidence intervals for the estimated age-dependent mean (Fig. 1B–N). To highlight differences in the sampled age range, the value of the spline fit at age 3 was subtracted from the values plotted; however, there were large differences between regions for several measures at that age (Supp. Fig. 2). In general, we observed marked differences among ROIs in the age-dependent spline fits. For example, whereas in primary visual cortex, cortical thickness decreased rapidly between ages 3 and 7 and then decreased more slowly between ages 10 and 21, caudal middle frontal gyrus (cMFG) exhibited slow cortical thinning in early childhood and then accelerated thinning during adolescence (Fig. 1B). For both primary auditory cortex and rostral middle frontal gyrus (rMFG), thickness decreased at an intermediate rate in early childhood and an accelerated rate in adolescence. Visual cortex also differed strongly from cMFG and rMFG in the developmental trends of LD, TD, and T2w in both gray matter and underlying white matter (Fig. 1G-H, K-N).

As a statistical test of the difference between two ROIs for a given measure, we calculated within-subject, pairwise differences for each combination of ROIs, and then used univariate linear regression to fit a quadratic function of age to those pairwise differences. We derived estimates of the differences at age 3 (intercept) and the combined effect of age and age-squared (between ages 3 and 21; Table 1, Table 2, Supp. Tables 1 and 2, Supp. Fig. 3; see Univariate Regressions). To test for aggregate differences between each pair of ROIs, we used multivariate regression on the pairwise differences between ROIs, producing F-statistics that reflect how different two regions of cortex are from each other with respect to age-related, developmental trajectories across multiple measures (Table 3; see Multivariate Regression). Using this approach, we found statistically significant differences between each pair combination of the four ROIs.

Table 1.

Effect sizes (Cohen's d) of the intercepts of inter-regional differences in imaging measures (at age 3) for selected anatomically defined cortical regions. * indicates inter-regional differences with p < 0.05, with Bonferroni correction for multiple comparisons.

ROI A	VC	VC	VC	cMFG	cMFG	rMFG
ROI B	cMFG	rMFG	AC	rMFG	AC	AC
FA gm	-0.1	-0.1	-0.2 *	-0.1	-0.1 *	-0.1
FA wm	-0.4 *	-0.4 *	-0.2 *	0.1	0.1	0.0
MD gm	0.0	0.0	-0.1	0.0	-0.1	-0.1
MD wm	0.0	0.0	0.0	0.0	0.0	0.0
LD gm	0.0	0.0	-0.1	0.0	-0.1 *	-0.1
LD wm	-0.2 *	-0.2 *	-0.1	0.0	0.1	0.1
TD gm	0.0	0.0	0.0	0.1	-0.1	-0.1
TD wm	0.1	0.1	0.1	0.0	0.0	0.0
T1w gm	0.5 *	0.3 *	-0.4 *	-0.2 *	-1.0 *	-0.6 *
T1w wm	0.0	0.1	-0.3 *	0.1	-0.4 *	-0.4 *
T2w gm	-0.2 *	-0.2 *	-0.3 *	-0.1	-0.1	0.0
T2w wm	-0.1	-0.1	-0.2 *	-0.1 *	-0.2 *	-0.1
area	0.1	0.0	0.2 *	-0.1 *	0.2 *	0.3 *
thickness	-0.4 *	-0.5 *	-0.6 *	-0.2 *	-0.3 *	-0.2 *
sulcal depth	0.0	0.4 *	-0.5 *	0.5 *	-0.7 *	-1.1 *

Table 2.

F-statistics for the trend of inter-regional differences in imaging measures with respect to age and age squared for selected anatomically defined cortical regions. * indicates inter-regional differences with p < 0.05, with Bonferroni correction for multiple comparisons.

ROI A	VC	VC	VC	cMFG	cMFG	rMFG
ROI B	cMFG	rMFG	AC	rMFG	AC	AC
FA gm	2.6	15.2 *	0.6	14.3 *	4.6	13.9 *
FA wm	14.6 *	10.8 *	5.1	80.5 *	3.4	18.3 *
MD gm	90.2 *	22.9 *	36.7 *	94.7 *	18.5 *	12.4 *
MD wm	131.3 *	39.2 *	86.5 *	111.7 *	10.4 *	24.5 *
LD gm	114.3 *	31.3 *	46.4 *	44.8 *	20.9 *	7.1
LD wm	108.3 *	63.7 *	56.3 *	29.3 *	5.2	6.7
TD gm	73.9 *	16.7 *	30.2 *	115.7 *	15.4 *	14.4 *
TD wm	117.7 *	21.7 *	61.9 *	143.7 *	7.4	25.6 *
T1w gm	75.2 *	0.6	18.9 *	60.1 *	9.1 *	10.2 *
T1w wm	6.3	12.4 *	2.0	3.1	1.9	4.6
T2w gm	71.7 *	28.6 *	34.0 *	34.9 *	15.0 *	7.5
T2w wm	78.7 *	56.3 *	109.8 *	10.8 *	0.6	5.8
area	1.6	2.8	0.1	18.7 *	1.3	3.9
thickness	37.7 *	62.1 *	12.9 *	239.0 *	25.1 *	16.9 *
sulcal depth	7.9	6.0	38.5 *	11.2 *	30.0 *	61.6 *

3.2. Cortical parcellation based on vertex-wise multimodal developmental trajectories

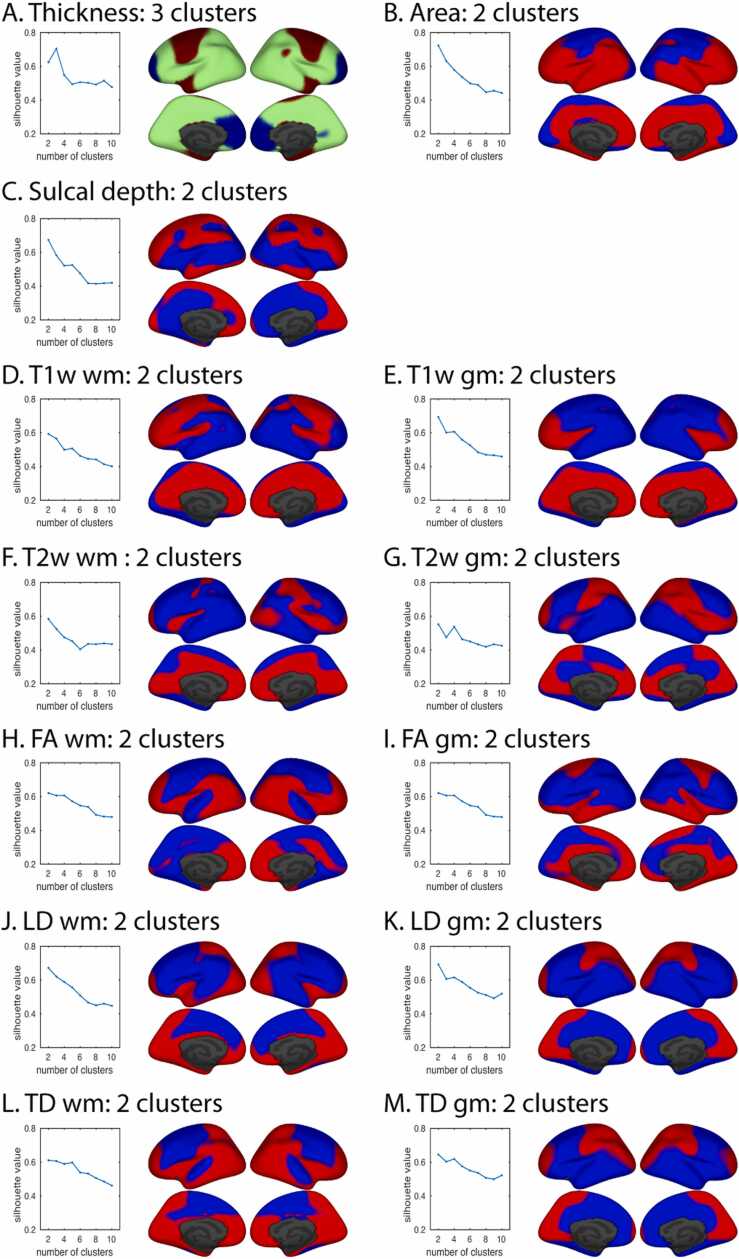
We then extended the analyses of developmental trajectories within specific prefrontal regions, as compared to primary visual and auditory cortex, that were driven by studies of direct neuronal measures to an empirical analysis of inter-regional variability in trajectories across the entire cortical surface, using parcellations from a data-driven, fuzzy clustering approach (see Cortical Parcellation with Fuzzy Clusters). Cluster membership was determined so as to minimize differences within clusters while maximizing differences in developmental trajectories between clusters. For single measures and the combination of multiple measures, we generated fuzzy cluster solutions for varying numbers of clusters, ranging from 2 to 10, and we used the corresponding silhouette values to determine the number of clusters supported by the data. The shape of the silhouette plots varied between the individual measures (Fig. 2). For thickness, the silhouette value was highest for three clusters (Fig. 2A). For all other measures, peak silhouette value was highest for two clusters. In general, cluster membership was remarkably symmetric across hemispheres. Despite similarity of the two-cluster solutions for some of the measures, there was not a strong consensus overall in the cortical subdivisions across measures (Fig. 2B–M).

Fig. 2.

Fuzzy cluster parcellations derived from univariate inter-regional differences in developmental trajectories. Silhouette values for a given imaging-derived measure, plotted as a function of the number of clusters, are shown next to inflated surfaces of left and right hemispheres, with lateral views above and medial views below. A. cortical thickness. B. cortical area. C. sulcal depth. D. T1w in pericortical white matter (wm). E. T1w in cortical gray matter (gm). F. T2w wm. G. T2w gm. H. FA wm. I. FA gm. J. LD wm. K. LD gm. L. TD wm. M. TD gm.

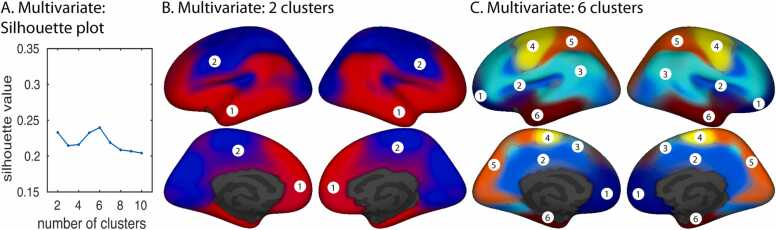
For clusters derived from multivariate analysis, silhouette values were maximal for six clusters, with another local maximum for two clusters (Fig. 3A). The distributed nature of the six-cluster solution makes it difficult to assign them names that are both succinct and anatomically accurate, so we have instead given them arbitrary cluster numbers. These clusters can be described anatomically as follows: 1) medial prefrontal cortex and frontal pole; 2) cingulate cortex and anterior medial occipital cortex; 3) prefrontal, superior temporal, inferior parietal, and medial parietal cortex; 4) central sulcus, precentral sulcus, and medial superior frontal cortex; 5) occipital and parietal cortex; and 6) temporal cortex. For the two-cluster solution, the first cluster had substantial overlap with clusters 1, 3, and 6 from the six-cluster solution, and the second cluster overlapped with clusters 2, 4, and 5 (Fig. 3B, C). To validate the generalizability of the six-cluster solution, we randomly split the sample into two halves and repeated the distance matrix calculations and determination of cluster membership. The two independent solutions were nearly identical (Supp. Fig. 2A, B). The split-half analysis was carried out for ten iterations, and the similarity of the six-cluster solutions for the randomly split two halves was assessed by calculating the adjusted Rand index (ARI), a corrected-for-chance measure of similarity between parcellations (Hubert and Arabie, 1985, Rand, 1971). ARI values greater than 0 imply better-than-chance similarity. Values close to 1 (the maximum possible ARI), imply highly consistent parcellations. Across the ten iterations, ARI ranged from 0.56 to 0.82, with a mean value of 0.73 and a standard deviation of 0.09. We conducted a similar analysis with the subsets of male and female participants, and again the cluster solutions were very similar (Supp. Fig. 2C, D), with an ARI of 0.73.

Fig. 3.

Fuzzy cluster parcellations derived from multivariate inter-regional differences in developmental trajectories. A. Silhouette values plotted as a function of the number of clusters for multivariate analysis. B. Two-cluster multivariate parcellation. C. Six-cluster multivariate parcellation.

3.3. Multimodal developmental trajectories of data-driven fuzzy clusters

We characterized how the developmental trajectories of the various imaging-derived measures differed between these distributed, fuzzy clusters. Within each subject, and for each cluster, we calculated weighted averages (weighted by the fuzzy cluster membership values, which range from 0 to 1) of each imaging-derived measure. We used univariate regression to estimate the intercept of the differences and the combined effect of age and age squared (between ages 3 and 21). In general, there were several significant differences between clusters in a number of imaging-derived measures for both intercept and age-related trajectories (Supp. Tables 3–7). Differences in age-dependent means were expected, given that the parcellation method was driven by a multivariate regression of age-related differences. To visualize these differences, we plotted the cluster-wise average values as a function of age for the two-cluster (Fig. 4 with age 3 adjusted values, Supp. Fig. 5 with unadjusted values) and six-cluster solutions (Fig. 5 with age 3 adjusted values, Supp. Fig. 6 with unadjusted values). We used smooth spline fits to describe the cross-sectional, developmental trajectories and bootstrap resampling to calculate 95% confidence intervals for the estimated mean as a function of age. To provide a simplified view of these results, we also plotted a summary of the cross-sectional changes for each cluster of the two- and six-cluster solutions (Supp. Fig. 7).

Fig. 4.

Developmental trajectories of imaging-derived measures for two-cluster multivariate parcellation. A. Two cortical regions are shown on inflated surface of right hemisphere; medial view on left, lateral view on right. B - G. Spline fits and 95% confidence intervals for each ROI, plotted relative to values at age 3 (i.e., the fitted value at age 3 was subtracted from each point along the displayed trajectory). B. cortical thickness (mm). C. area (mm² / vertex). D. sulcal depth (unitless). E. T1w in pericortical white matter (wm) (arbitrary units: AU). F. T1w in cortical gray matter (gm) (AU). G. T2w wm (10⁻³ mm²/s). H. T2w gm (10⁻³ mm²/s). I. FA wm (unitless). J. FA gm (unitless). K. LD wm (mm²/s). L. LD gm (mm²/s). M. TD wm (mm²/s). N. TD gm (mm²/s).

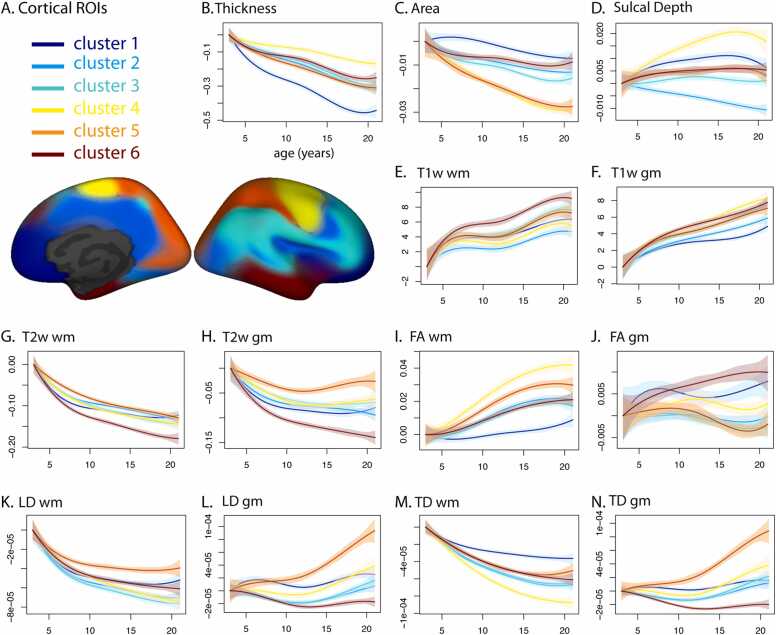
Fig. 5.

Developmental trajectories of imaging-derived measures for six-cluster multivariate parcellation. A. Six cortical regions are shown on inflated surface of right hemisphere; medial view on left, lateral view on right. B - G. Spline fits and 95% confidence intervals for each ROI, plotted relative to values at age 3. B. cortical thickness (mm). C. area (mm² / vertex). D. sulcal depth (unitless). E. T1w in pericortical white matter (wm) (arbitrary units: AU). F. T1w in cortical gray matter (gm) (AU). G. T2w wm (10⁻³ mm²/s). H. T2w gm (10⁻³ mm²/s). I. FA wm (unitless). J. FA gm (unitless). K. LD wm (mm²/s). L. LD gm (mm²/s). M. TD wm (mm²/s). N. TD gm (mm²/s).

We found striking differences between the six clusters in the cross-sectional, developmental trajectories of measures derived from morphometric analysis of sMRI data as well as dMRI-derived and sMRI intensity measures for both pericortical white matter and cortical gray matter (Fig. 5). Cluster 1 differed noticeably from the others based on the trajectories of multiple measures. Cortical thickness appeared to decrease sharply in early childhood and adolescence, contrasting with more gradual decreases in the other clusters. Cluster 1 exhibited a slight increase in cortical surface area in early childhood that reversed direction later, whereas clusters 4 and 5 both had a steeper surface area decrease across the age range. Trajectories for cluster 1 also differed for FA and TD in white matter, with very gradual increases or decreases, respectively, across the age range. In contrast, clusters 4 and 5 had steeper, more nonlinear increases in FA and decreases in TD. In general, trajectories of white matter diffusivity varied between clusters, but in ways that were not consistent between LD and TD. For example, whereas cluster 1 had the shallowest decrease in TD and cluster 4 had the steepest, their trajectories for LD were relatively similar. In gray matter, LD and TD trajectories were very similar to each other. The developmental trajectories of cluster 5 were most distinct, being relatively flat until about age 12, after which there was a steep increase in both LD and TD. The other clusters, in contrast, exhibited slight decreases in gray matter diffusivity before age 12 with modest increases thereafter. Gray matter T2w also differed between clusters, with the steepest decrease for cluster 6 and shallowest decrease for cluster 5. To illustrate the variation of trajectories within clusters, we also plotted trajectories for individual vertices within each cluster (Supp. Fig. 8).

The cortico-cortical “distance” metric used to inform the fuzzy clustering algorithm was based solely on the multivariate relationship with age, and not the static, age-independent differences between cortical locations. Nonetheless, there were substantial differences between regions at the youngest ages sampled for several measures, including thickness, sulcal depth, white matter and gray matter FA, and white matter LD (Supp. Fig. 6, Supp. Table 3). For example, initial cortical thickness was greatest for clusters 1 and 6 and least for cluster 5. There did not appear to be a consistent relationship between sulcal depth and cortical thickness. For example, clusters 5 and 6 had similar sulcal depth values but maximally-different thickness values at age 3. Initial values of white matter LD and TD varied between clusters, but in ways that were not consistent between LD and TD. For example, cluster 2 had one of the top three LD values at age 3, but the lowest TD. There were also differences between clusters in the age 3 FA values in gray and white matter, but the ordering was not consistent. For example, for white matter FA, cluster 6 was ranked in the bottom three, whereas for gray matter FA, cluster 6 was in the top two.

4. Discussion

The current results demonstrate that the nonlinear developmental trajectories of cortical surface-based measures derived from a combination of structural imaging modalities do indeed vary regionally, and they show which individual brain measures seem to contribute most strongly to changes at different developmental phases. These observations are consistent with the differences in synaptic density observed in early post-mortem histological studies between early sensory areas and prefrontal cortex, such as in studies by Huttenlocher and colleagues (e.g., Huttenlocher and Dabholkar, 1997). Our broader analysis provides a more complicated picture of inter-regional variation, however. For example, differences in developmental trends observed between two early sensory regions and between two adjacent prefrontal cortical regions demonstrated a surprising degree of heterogeneity within the cortex, even in regions close to one another or related in overall function. Furthermore, the developmental trajectories of the cortical measures differed from one another and demonstrated distinct spatiotemporal patterns of differences across age. Whereas cortical thickness in visual cortex reached near-mature levels by early adolescence, other measures, such as cortical surface area or diffusivity in cortical gray matter continue changing in late adolescence.

The developmental trajectories of estimated cortical thickness are presumably influenced by changes in synaptic density, but other cellular changes, such as iron deposition, could potentially alter T1-weighted intensities so as to slightly bias the placement of the gray-white boundary (Drayer et al., 1986, Hallgren and Sourander, 1958). The other measures tested in this study, including morphometric measures cortical area and sulcal depth, microstructural measures diffusivity and anisotropy, and image intensity measures, may also be influenced by these or other cellular changes that occur during childhood and adolescence. Based on the differences between imaging measures in trajectories and clustering results, it appears that there are multiple neurobiological features that unequally influence the developmental trajectories of the individual imaging measures. If attempting to assess the maturity of a given cortical region relative to other cortical regions, reliance on a single imaging-derived measure provides an incomplete picture of the developmental changes taking place. Our findings build upon much previous work examining developmental regional differences in cortical neuroanatomy that have used both univariate (Fjell et al., 2018, Fjell et al., 2012, Giedd et al., 1999, Gogtay et al., 2002, Lebel and Beaulieu, 2011, Sowell et al., 2003) and multivariate (Brown et al., 2012) approaches for delineating age trajectories in typically developing preschoolers, school-age children, adolescents, and young adults. The advantage of the current multivariate approach is that it uses the aggregate of all available measures, producing probabilistic estimates of similarities and differences to inform interregional comparisons of developmental trajectories across all of these age groups.

Consistent with the general conclusions of classic and highly influential histological studies, our results suggest that primary sensory cortical areas can be distinguished from transmodal association areas by the trajectory characteristics of both their morphology and tissue properties and that prefrontal regions show a protracted period of greater developmental change relative to sensory regions for at least some imaging measures. Given the unexpected heterogeneity we found of some close-lying prefrontal cortex regions and across the cortex in general, questions about the spatial patterns of inter-regional differences and similarities may require a data-driven, cortex-wide approach like we have used here. Using vertex-wise analyses to examine developmental differences across the entire cortical surface, cluster maps revealed empirically derived divisions of the cortex that show significantly different developmental trajectories, using either single measures of morphology or diffusion properties, or a multivariate combination of all measures. Maps derived from univariate measures varied in the number of clusters produced based on their silhouette values. A three-cluster solution was optimal for cortical thickness, and a two-cluster solution was optimal for all other measures. The two-cluster maps varied considerably from one another, dividing roughly along either dorsal/ventral, caudal/rostral, or pre-/post-central dimensions, depending on the measure.

Analyses of vertex-wise developmental trajectory differences using the multivariate combination of all measures generated two maps with the highest silhouette values, one with two regional divisions and another with six divisions. Both maps showed strong similarities between left and right cerebral hemispheres. The two-cluster map yielded a strong difference between dorsal and ventral cortical regions, which divided primary sensory, tertiary, and primary motor areas (visual, extrastriate, auditory, somatosensory, motor and premotor cortex) from transmodal association areas of the lateral parietal, temporal, and prefrontal lobes, including anterior portions of the medial temporal and prefrontal cortex. The dorsal cluster showed relatively greater change from preschool through adolescence in cortical surface area and similar change in cortical thickness as compared to the ventral cluster. The ventral cluster showed greater developmental change than the dorsal cluster in sulcal depth over this age range. For measures of diffusivity within pericortical white matter, the dorsal cortical cluster showed greater changes with age in FA. All diffusion measures within cortical gray matter showed relatively greater age changes within the dorsal cluster as compared to the ventral cluster. Across all measures except sulcal depth and thickness, the dorsal developmental division showed relatively greater age-related changes than the ventral division between 3 and 21 years of age. These results provide an interesting multimodal, multidimensional characterization of the cerebral “what” and “where” pathways, suggesting at least broadly that the former systems show less maturational change anatomically than the latter, at least across the ages we studied here and according to this specific collection of measures (de Haan and Cowey, 2011, Freud et al., 2016, Goodale and Milner, 1992, Mishkin and Ungerleider, 1982, Schneider, 1969). The six-cluster developmental parcellation made further subdivisions of the two-cluster dorsal and ventral regions, separating each into smaller sub-regions with maximally divergent developmental trajectories.

While reproducing some findings on regional variability in the cortex, and producing some novel results based on a developmental trajectory clustering method, our study also helps to demonstrate some of the challenges inherent in attempting to characterize and make conclusions about the relative maturational rates and phases of different brain regions. By delineating and quantifying developmental slopes, we can estimate whether trajectories differ. But conclusions about whether a particular brain region “has matured” (i.e., has reached a biological state of maturity or has crossed some likely arbitrary threshold of maturity) or that one brain region matures faster and earlier or slower and later than another is still not entirely straightforward precisely because of the arbitrariness in operationally defining maturity as an end state. For example, our approach shows that although primary sensory cortex has a shallower slope than prefrontal cortex it is, nevertheless, still changing across the ages examined here and likely continues to change throughout adulthood, albeit in subtler fashion. So, at what age is visual cortex “mature”? As evidence from lifespan studies strongly suggests, questions about brain development framed in this way are likely simplistic and misleading, given the inconstant nature of the brain (Lebel et al., 2012, Sowell et al., 2003, Tamnes et al., 2013, Walhovd et al., 2016, Ziegler et al., 2012). We suggest caution in the use and potential oversimplification of these terms and concepts in the literature.

Individual variability in rates and trajectories of brain development also need to be considered and examined when looking at characterizations based on group averages. The individual differences variability for most brain measures at a given age is relatively large compared to the developmental phase variability across age for the same measure (e.g., Brown et al., 2012). This reality makes the characterization of trends, rates, phases, timing, maturational endpoints, and trajectories difficult to fully convey with metrics based solely on central tendency. Longitudinal studies will be particularly useful for characterizing how inter-individual variability relates to change in specific brain measures over time (Mills et al., 2021).

One approach that has been used previously in developmental imaging research to determine the age of maturity or the relative maturation order between different brain regions has been to compare the age peaks of quadratic trend fits for a given measure (Giedd et al., 1999, Giedd et al., 2010, Shaw et al., 2006, Sowell et al., 2003). This practice may lead to misleading conclusions for several reasons: it artificially forces a peak to be placed at a particular age where one might not exist (Fjell et al., 2010), many measures likely have no single or obvious peak (i.e., are monotonic), and as we have shown here when using data-driven spline fits, many measures simply do not stop changing with age and development.

One of the primary limitations of our study is that we computed developmental trajectories based on cross-sectional data, inferring age change from what are really age differences. Cross-sectional analyses can produce misleading results if, for example, there are significant differences across age in subject characteristics that may relate to the dependent measures. For this reason, we controlled all trajectory analyses for variables known or suspected to have such effects (e.g., socioeconomic status, sex, genetically determined ethnic ancestry; Fan et al., 2015, Lenroot and Giedd, 2010, Noble et al., 2015). Similarly, small but significant variation between scanners is unavoidable, and between scanner manufacturers even more so. Because of that, we also included regressors to account for the variation of the means across scanner instances (Brown et al., 2012). It is also worth noting that we were guided by developmental differences observed in histochemical, postmortem studies that were also performed cross-sectionally. Nevertheless, the use of longitudinal imaging measures would provide a more direct assessment of differences in developmental changes across different cortical regions, and the recent availability of longitudinal data sets are making this more possible (e.g., Fjell et al., 2018). For example, the large Adolescent Brain Cognitive Development (ABCD) Study is ongoing and will eventually span ages 9–20 (Casey et al., 2018, Hagler et al., 2019). Note that in order to test the questions across the age range we’ve addressed here using cross-sectional data, a longitudinal data set following preschoolers for 17 years would be required.

Cortical parcellation methods and mapping are becoming more commonplace, but the use of multivariate statistical analyses of developmental trajectories is relatively rare, especially using measures integrated from different modalities (e.g., diffusion, morphometry). Multivariate nonlinear developmental modeling has been shown to provide significant advantages over univariate approaches for assessing developmental phase changes in features known to have complex, multifactorial neurobiological contributors and high individual differences variability in any single measure at any given age (Brown et al., 2012, Dosenbach et al., 2010). By examining developmental trajectories cross-sectionally in a relatively large sample spanning the preschool to adolescent ages, using an integrated multimodal, multivariate, nonlinear trajectory approach, our study provides new evidence that corroborates some limited but highly influential early histological work and suggests new directions for continuing to develop methods for characterizing human brain development.

Funding

This work was supported by a grant from the National Institute on Drug Abuse awarded to Natacha Akshoomoff and Timothy T. Brown (R01DA038958). Data collection and sharing for this project were funded by the National Institute on Drug Abuse and the Eunice Kennedy Shriver National Institute of Child Health and Human Development (Grants RC2DA029475 and R01HD061414). Chi-Hua Chen was supported by a grant from the National Institute of Mental Health (R01MH118281). Donald Hagler was also supported by a grant from the National Institute on Drug Abuse (U24DA041123).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material

.

Supplemental Figure 1

Flow-chart depicting step-wise, QC-related exclusions.

.

Supplemental Figure 2

Unadjusted developmental trajectories of imaging-derived measures in anatomically defined cortical regions. A. Selected cortical regions of interest are labeled on inflated surfaces of right hemisphere; medial view on left, lateral view on right. B - G. Spline fits and 95% confidence intervals for each ROI, plotted without removing differences at age 3. B. cortical thickness (mm). C. area (mm² / vertex). D. sulcal depth (unitless). E. T1w in pericortical white matter (wm) (arbitrary units: AU). F. T1w in cortical gray matter (gm) (AU). G. T2w wm (10⁻³ mm²/s). H. T2w gm (10⁻³ mm²/s). I. FA wm (unitless). J. FA gm (unitless). K. LD wm (mm²/s). L. LD gm (mm²/s). M. TD wm (mm²/s). N. TD gm (mm²/s).

.

Supplemental Figure 3

Comparison of inter-regional differences in intercept and trend for selected anatomically defined cortical region pairs. Scatter plots show -log10 p-values (corrected for multiple comparisons with Bonferroni method) for intercept and trend across phenotypes for each pair of ROIs. These plots are a visualization of the results in Supp. Tables 1 and 2.

.

Supplemental Figure 4

Fuzzy clusters derived from multivariate, inter-regional differences in developmental trajectories for subsets of participants. A. Clusters from randomly chosen first half of participants. B. Clusters from a second, complementary set of participants. C. Clusters derived from female participants. D. Clusters from male participants. Inflated surfaces of left and right hemispheres on left and right, with lateral views above and medial views below.

.

Supplemental Figure 5

Unadjusted developmental trajectories of imaging-derived measures for two-cluster multivariate parcellation. A. Two cortical regions are shown on inflated surface of right hemisphere; medial view on left, lateral view on right. B - G. Spline fits and 95% confidence intervals for each ROI, plotted without removing differences at age 3. B. cortical thickness (mm). C. area (mm² / vertex). D. sulcal depth (unitless). E. T1w in pericortical white matter (wm) (arbitrary units: AU). F. T1w in cortical gray matter (gm) (AU). G. T2w wm (10⁻³ mm²/s). H. T2w gm (10⁻³ mm²/s). I. FA wm (unitless). J. FA gm (unitless). K. LD wm (mm²/s). L. LD gm (mm²/s). M. TD wm (mm²/s). N. TD gm (mm²/s).

.

Supplemental Figure 6

Unadjusted developmental trajectories of imaging-derived measures for six-cluster multivariate parcellation. A. Six cortical regions are shown on inflated surface of right hemisphere; medial view on left, lateral view on right. B - G. Spline fits and 95% confidence intervals for each ROI, plotted without removing differences at age 3. B. cortical thickness (mm). C. area (mm² / vertex). D. sulcal depth (unitless). E. T1w in pericortical white matter (wm) (arbitrary units: AU). F. T1w in cortical gray matter (gm) (AU). G. T2w wm (10⁻³ mm²/s). H. T2w gm (10⁻³ mm²/s). I. FA wm (unitless). J. FA gm (unitless). K. LD wm (mm²/s). L. LD gm (mm²/s). M. TD wm (mm²/s). N. TD gm (mm²/s).

.

Supplemental Figure 7

Summary of cross-sectional change in two- and six-cluster parcellations. Cross-sectional change was calculated from spline fit trajectories shown in Fig. 4, Fig. 5. Change was calculated relative to the spline fit values at age 3 by subtracting the value at age 3 from all other values, then dividing by the original value at age 3, then selecting the relative difference value with the maximum absolute value across the age range 3–21. Relative differences for each ROI are plotted as percent change as a function of imaging-derived measure. A. Two-cluster parcellation. B. Six-cluster parcellation.

.

Supplemental Figure 8

Vertex-wise trajectories for cortical thickness and FA in white matter. Trajectories are shown for individual vertices within each cluster (5% of all vertices in each cluster, with icosahedral order = 4) as well as the mean and standard deviation of trajectories across vertices.

.

Data Availability

I have shared links to data and code in the Attach File step.