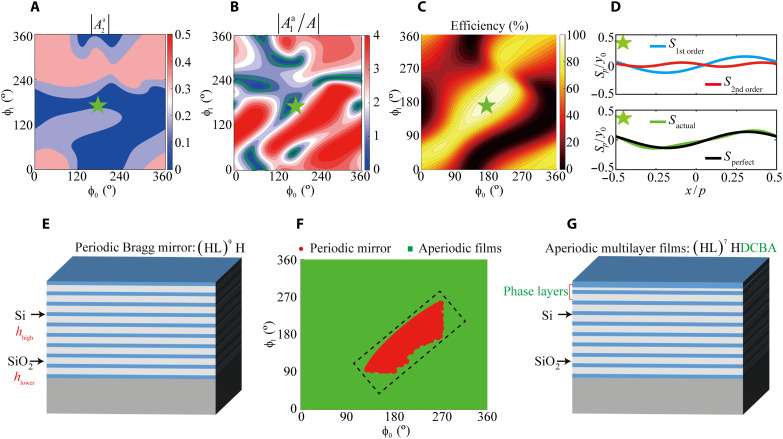
Fig. 2. Nonlocal design for 40° perfect anomalous reflection.

The nonlocal response of perfect anomalous reflection is realized by changing only the phase responses ϕ₀ and ϕ₁ of multilayer films with a given spacer and gradient gratings. The geometric parameters of the six elements are listed. The height of the six elements is 500 nm, and the widths are 71, 161, 201, 217, 236, and 356 nm. (A) The relation of phase responses ϕ₀ and ϕ₁ with respect to the second-order amplitude of actual lateral energy transfer S^a. (B) The relation of phase responses ϕ₀ and ϕ₁ with respect to the first-order amplitude of actual lateral energy transfer S^a. The actual first-order amplitude is normalized by the desired amplitude. (C) The anomalous-reflection efficiency versus phase responses ϕ₀ and ϕ₁. The perfect anomalous reflection is marked by the green pentagram. (D) Distributions of the second- and first-order oscillations when ϕ₀ and ϕ₁ are (173°, 170°), respectively. (E) Schematic diagram of the periodic Bragg mirror. (F) Phase combination realized by the periodic Bragg mirror and aperiodic multilayer films. The phase responses ϕ₀ and ϕ₁ of the Bragg mirror are changed with the thickness. For aperiodic multilayer films, an arbitrary phase combination (ϕ₀, ϕ₁) and near 100% reflectance can be obtained simultaneously by changing the thickness of the four outermost phase layers. (G) Schematic diagram of the aperiodic multilayer films. The periodic Bragg mirror and four phase layers control the amplitude and phase, respectively.