Abstract
Mendelian randomization (MR) is a common tool for identifying causal risk factors underlying diseases. Here, we present a method, MR with automated instrument determination (MRAID), for effective MR analysis. MRAID borrows ideas from fine-mapping analysis to model an initial set of candidate single-nucleotide polymorphisms that are in potentially high linkage disequilibrium with each other and automatically selects among them the suitable instruments for causal inference. MRAID also explicitly models both uncorrelated and correlated horizontal pleiotropic effects that are widespread for complex trait analysis. MRAID achieves both tasks through a joint likelihood framework and relies on a scalable sampling–based algorithm to compute calibrated P values. Comprehensive and realistic simulations show that MRAID can provide calibrated type I error control and reduce false positives while being more powerful than existing approaches. We illustrate the benefits of MRAID for an MR screening analysis across 645 trait pairs in U.K. Biobank, identifying multiple lifestyle causal risk factors of cardiovascular disease–related traits.
MRAID is a statistical method for effective and calibrated MR analysis, enabling large-scale screening of causal risk factors.
INTRODUCTION
Investigating causal relationship among complex traits and identifying causal risk factors are an important first step toward understanding the biology of diseases. A common statistical tool for performing this causal inference in observational studies is Mendelian randomization (MR). MR is a form of instrumental variable analysis that uses single-nucleotide polymorphisms (SNPs) to serve as instruments for inferring the causal effect of an exposure on an outcome (1). MR requires only summary statistics from genome-wide association studies (GWASs) and is often performed in a two-sample study setting where the exposure and the outcome are measured in two separate studies (2). With the abundant availability of GWAS summary statistics, numerous MR analyses are being carried out, identifying important causal risk factors for various diseases. These MR studies are facilitated by many recently developed MR methods, which include the inverse variance weighted (IVW) method, MR-Egger (3), median-based regression (4), Bayesian weighted MR (BWMR) (5), robust adjusted profile score (RAPS) (6), MRMix (7), and Causal Analysis Using Summary Effect estimates (CAUSE) (8), to name a few. However, most of the current MR methods encounter two important modeling and algorithmic challenges that have so far limited the effectiveness of MR analysis.
First, almost all existing MR methods rely on a preselected set of independent SNPs to serve as instruments for MR analysis. The instruments are selected to be independent from each other to ensure the validity of the statistical inference framework used in many common MR methods such as IVW. The independent SNPs are often selected through linkage disequilibrium (LD) clumping, a procedure that first ranks SNPs on the basis of their marginal association evidence with the exposure and then retains SNPs that are not in high LD with the SNPs on top of the ranking list. Using LD clumping to select SNPs may be suboptimal, however, as the selected SNPs only represent tagging SNPs that often explain a smaller phenotypic variance than the causal ones and only contain independent SNPs that may be unable to capture additional variance explained from the other regional variants (9–12). The parallel field of GWAS fine mapping highlights the benefits of performing SNP selection through formal modeling–based approaches (9, 10, 13–16). Consequently, using a formal SNP selection procedure for identifying instruments instead of directly using the tagging SNPs may help increase the power of MR analysis. In addition, complex traits can be influenced by multiple causal SNPs residing in the same local region that are in potential LD with each other. Consequently, selecting independent SNPs may only capture a small proportion of the phenotypic variance in the exposure variable (17, 18), again leading to a loss of power in the subsequent MR analysis (1, 2, 19, 20). In the parallel field of transcriptome-wide association studies (TWASs), it has been well documented that incorporating correlated SNPs can substantially improve gene expression prediction accuracy (21) and, consequently, the power of TWASs (17, 22–24). Therefore, incorporating correlated SNPs and developing effective approaches to select instruments among them are important to fully captivate the potential of MR.
Second, only a limited number of MR methods model horizontal pleiotropy, and even fewer can effectively control for it (17, 25). Horizontal pleiotropy occurs when the SNP instruments exhibit effects on the outcome through pathways other than the exposure. Horizontal pleiotropy often comes in two distinct types: The first type arises through paths independent of the exposure with horizontal pleiotropic effects independent of the SNP effects on the exposure; the second type arises through unobserved exposure-outcome confounders and induces correlation between the horizontal pleotropic effects and the SNP effects on the exposure. For example, insulin resistance (IR) occurs when excess glucose in the blood reduces the ability of the cells to absorb and use blood sugar for energy. IR is an important cause of type II diabetes (T2D) (26) and also has profound effects on lipoproteins, such as low-density lipoprotein (LDL) (27). When investigating the causal effect of LDL on T2D, the selected candidate instrumental SNPs may include IR-associated SNPs. These IR-associated SNPs are likely to be associated with both LDL and T2D, leading to correlated pleiotropy in the MR analysis. The presence of either type of horizontal pleiotropy violates standard MR modeling assumptions and can lead to biased causal effect estimates and increased false discoveries. Early MR analyses control for horizontal pleiotropy by simply removing instrumental SNPs that are potentially associated with the outcome variable (25, 28–30). Removing SNPs associated with the outcome would result in a conservative set of selected instruments and lead to a loss of MR power. Recent MR methods explicitly model horizontal pleiotropic effects. For example, the Egger assumption assumes the same horizontal pleiotropic effect across SNP instruments (3, 17), while Probabilistic Mendelian randomization with Variance Component (PMR-VC) (17) and BWMR (5) assume the horizontal pleiotropic effects to follow a normal distribution; all these methods model the first type of horizontal pleiotropy. MRMix (7) and CAUSE (8), by contrast, use a normal-mixture model to control for both types of horizontal pleiotropy. Unfortunately, modeling both types of horizontal pleiotropy has been technically challenging, as the resulting likelihood function of the MR model often consists of an integration that cannot be solved analytically. Consequently, both MRMix and CAUSE rely on non-likelihood–based approaches to perform inference. Specifically, MRMix searches on a grid of causal effect candidates to identify the one that maximizes the proportion of GWAS summary statistics residing in the expected submodel without horizontal pleiotropy. CAUSE contrasts the out-of-sample prediction accuracy between two different models, one with the causal effect and the other without, by computing the expected log pointwise posterior density between the two, for causal inference. Non-likelihood–based causal inference, however, can lead to a loss of power and/or uncalibrated test statistics that are essential for large-scale screening of causal risk factors underlying diseases. As we will show here, MRMix is not robust to modeling misspecifications on the instrumental effect sizes and is prone to estimation bias, while CAUSE yields overly conservative P values.
Here, we present a likelihood-based two-sample MR method for causal inference that overcomes the above two challenges. Specifically, our method models an initial set of candidate SNP instruments that are in high LD with each other and automatically selects among them the suitable instruments for MR analysis. In addition, our method accounts for both types of horizontal pleiotropy in a likelihood framework and relies on a scalable sampling–based algorithm for calibrated P values computation. We refer to our method as the two-sample MR with automated instrument determination (MRAID). We demonstrate the effectiveness of MRAID through comprehensive and realistic simulations. We also apply MRAID for an MR screening analysis across 645 trait pairs in the U.K. Biobank (31), identifying lifestyle risk factors that may causally influence cardiovascular disease–related traits.
RESULTS
Method overview and simple illustrative simulations
MRAID is described in Materials and Methods, with its technical details provided in Supplementary Text and a method schematic shown in Fig. 1. Briefly, MRAID is a two-sample MR method that aims to infer the causal effect of an exposure variable on an outcome variable using GWAS summary statistics. MRAID models jointly all genome-wide significant SNPs that are in potential LD with each other and performs automated instrument selection among them to identify suitable instruments for MR analysis. In addition, MRAID explicitly accounts for two types of horizontal pleiotropic effects through a maximum likelihood–based inference framework and is scalable to biobank datasets (Table 1). We carried out both simple and comprehensive simulations with a total of 46 null and 80 alternative scenarios (table S1).
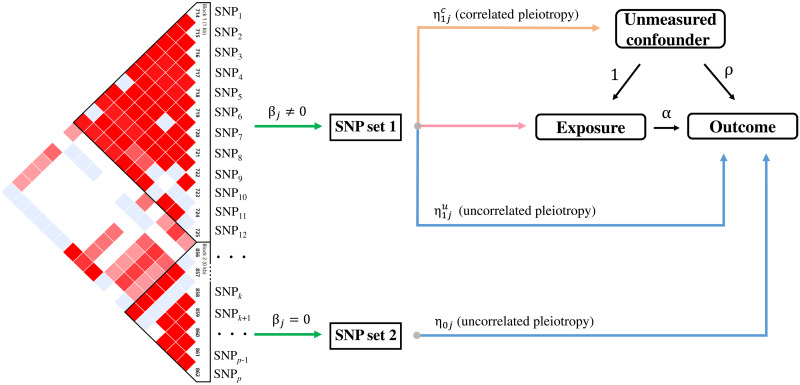
Fig. 1. Schematic of MRAID.
MRAID is an MR method that infers the causal effect of an exposure on an outcome in the presence of unmeasured confounder by using SNPs as instrumental variables. MRAID first obtains an initial set of candidate SNP instruments that are marginally associated with the exposure (SNP1, …, SNPp) and that are in potential LD with each other (LD plot on left). MRAID imposes a sparsity assumption on the instrumental effects of the candidate SNPs to divide instruments with nonzero effects (SNP set 1) and zero effects (SNP set 2) on the exposure. Among the selected instruments (SNP set 1), MRAID assumes that a proportion of them display horizontal pleiotropic effects that are uncorrelated with instrumental effects (blue path) and that another proportion of them display horizontal pleiotropic effects that are correlated with instrumental effects (orange path). Among the nonselected instrument candidates (SNP set 2), MRAID also assumes that a proportion of them display horizontal pleiotropic effects that are uncorrelated with instrumental effects (blue path). Overall, MRAID models jointly all genome-wide significant SNPs that are in potential LD with each other and performs automated instrument selection among them to identify suitable instruments. MRAID explicitly accounts for both correlated and uncorrelated horizontal pleiotropy and relies on a likelihood framework for effective and scalable inference.
Table 1. Mean computational time (in min) of various two-sample MR methods.
Computation is carried out on a single thread of a Xeon Gold 6138 CPU. The computation time is averaged across 20 replicates, with values inside parentheses denoting the SD. #SNPs denotes the number of instrumental variables included in the model. The computational time for MRAID is based on 1000 Gibbs sampling iterations with the first 200 as burn-in.
| #SNPs | MRAID | CAUSE | MRMix | IVW-R |
Weighted
mode |
Weighted
median |
RAPS | Robust |
| 1000 | 0.31(0.07) | 2.63(1.90) | 0.12(0.03) | 0.0001(0.00001) | 0.17(0.04) | 0.011(0.003) | 0.0004(0.0003) | 0.0004(0.0001) |
| 2000 | 1.57(0.26) | 2.99(2.24) | 0.13(0.03) | 0.0001(0.00001) | 0.18(0.03) | 0.012(0.002) | 0.0004(0.0006) | 0.0004(0.0001) |
| 3000 | 3.91(0.75) | 3.66(2.36) | 0.14(0.02) | 0.0001(0.00002) | 0.18(0.03) | 0.012(0.003) | 0.0004(0.0003) | 0.0004(0.0001) |
| 4000 | 6.82(1.35) | 4.24(1.62) | 0.15(0.04) | 0.0001(0.00003) | 0.18(0.04) | 0.013(0.003) | 0.0004(0.0001) | 0.0004(0.0002) |
| 5000 | 10.80(2.69) | 4.92(2.29) | 0.18(0.05) | 0.0001(0.00004) | 0.18(0.04) | 0.013(0.002) | 0.0004(0.0001) | 0.0005(0.0003) |
We first performed simple simulations to help build intuition and illustrate the benefits of modeling multiple correlated SNPs (details in Materials and Methods). Here, we only compared MRAID with the Wald ratio estimator, which is the MR method that uses only the top exposure-associated SNP as instrument (details in Materials and Methods). Consistent with the fine-mapping literature (9, 10, 13, 32), we found that the top variant is the casual SNP in only 53.6% of the simulation replicates. Because the top variant is not necessary the causal one, the Wald ratio estimator produces slightly deflated P values as documented in previous studies (fig. S1) (33). In contrast, MRAID produces calibrated type I error control due to its ability to perform automated instrumental selection (fig. S1). Because the same P value from different methods may correspond to different type I errors, we computed power on the basis of a false discovery rate (FDR) of 0.05 instead of a nominal P value threshold to allow for fair comparison among methods. In the power comparison, we found that MRAID is more powerful than the Wald ratio estimator regardless of the number of causal SNPs, the LD structure among different SNPs, and the presence or absence of the causal SNPs (fig. S2). Similar results are observed when comparing MRAID that uses the top two SNPs obtained from a stepwise regression with MRAID that uses only the lead SNP (fig. S3). These results highlight the benefits of modeling correlated SNPs and performing SNP selection for MR analysis.
Simulations: Type I error control
We performed comprehensive and realistic simulations to evaluate the performance of MRAID and compare it with seven existing MR methods (details in Materials and Methods). Different from the above simple illustrative simulations, we incorporated multiple complications that would occur in real data analysis into the comprehensive simulations. These complications include the presence of multiple variants and the presence of horizontal pleiotropy along with two distinct types of horizontal pleiotropy. In the comprehensive simulations, we also examined the benefits of instrumental selection in MRAID by comparing it to an oracle version where we assumed that the true instruments are known. These multiple complications introduced in the comprehensive simulations are important for consideration for real data MR analysis.
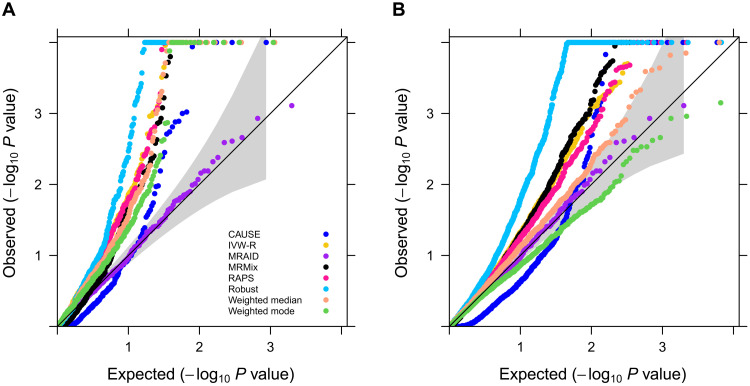
We first examined type I error control of different methods in different scenarios. In the absence of both correlated and uncorrelated horizontal pleiotropic effects, most methods—including MRAID, random effect version of the inverse variance-weighted method (IVW-R), Robust, RAPS, Weighted median, and MRMix—all yield reasonably calibrated type I error control (Fig. 2A). Weighted mode and CAUSE, on the other hand, display overly conservative type I error control, which is consistent with the original studies (7, 8, 34). The null P value distributions from different methods remain largely similar regardless of the number of SNPs that affect the exposure (fig. S4A) and their total effects on the exposure (fig. S4B). We further examined the robustness of different methods in settings where the SNP effects on the exposure do not follow a simple normal distribution but with some SNPs displaying larger effects than the others. In these settings, MRAID, IVW-R, and RAPS remain calibrated, while both MRMix and Robust methods show inflated type I errors, presumably due to their restricted normality assumptions on the SNP effect sizes (Fig. 2B). Note that we directly used correlated SNPs for MRAID but performed clumping to select independent SNPs for the other methods. Without clumping, all other MR methods produce overly inflated type I errors (fig. S5).
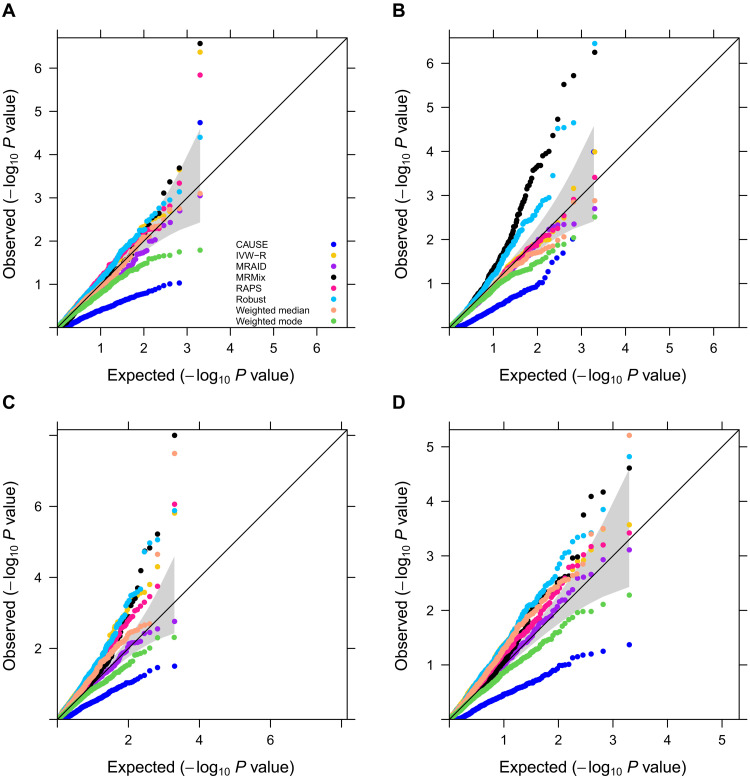
Fig. 2. Type I error control of different MR methods in simulations.
Type I error is evaluated by quantile-quantile plots of −log10 P values from different MR methods on testing the causal effect under the null simulations. Compared methods include CAUSE (blue), IVW-R (gold), MRAID (purple), MRMix (black), RAPS (deep pink), Robust (deep sky blue), Weighted median (light salmon), and Weighted mode (green). Four null simulation scenarios are examined. (A) Null simulations in the absence of both correlated and uncorrelated horizontal pleiotropic effects. We simulated 100 instrumental SNPs with their effect sizes drawing from a normal distribution. (B) Null simulations in the absence of both correlated and uncorrelated horizontal pleiotropic effects. We simulated 1000 instrumental SNPs with their effect sizes drawing from a Bayesian sparse linear mixed model (BSLMM) distribution with 1% SNPs having large effects and 99% SNPs having small effects. (C) Null simulations in the absence of correlated horizontal pleiotropic effect but in the presence of uncorrelated horizontal pleiotropic effect (PVEu = 5%). We simulated 100 instrumental SNPs and set the proportion of instrumental SNPs having uncorrelated horizontal pleiotropy to be 20%. (D) Null simulations in the presence of both correlated (πc = 5%, ) and uncorrelated horizontal pleiotropic effects (PVEu = 5%). We simulated 100 instrumental SNPs and set the proportion of instrumental SNPs having the uncorrelated horizontal pleiotropy effect to be 20%.
We examined the effects of horizontal pleiotropy on type I error control for different methods. When horizontal pleiotropic effects are present but are uncorrelated with the instrumental effects, MRAID maintains type I error control (Fig. 2C). In contrast, both Weighted mode and CAUSE remain overly conservative, while MRMix, Robust, IVW-R, Weighted median, and RAPS yield inflated P values (Fig. 2C). Similar conclusion holds regardless of the effect size for the uncorrelated horizontal pleiotropy or the proportion of SNPs that display uncorrelated pleiotropic effects (fig. S6). The P value inflation problem of MRMix and Weighted median relieves when the proportion of SNPs that display uncorrelated horizontal pleiotropic effects decreases. When correlated horizontal pleiotropic effects are also present in addition to the uncorrelated horizontal pleiotropic effects, MRAID maintains effective type I error control (Fig. 2D). In contrast, both Weighted mode and CAUSE remain overly conservative, while MRMix, Robust, IVW-R, Weighted median, and RAPS produce inflated P values. Similar conclusion holds regardless of the effect size of the correlated horizontal pleiotropy (fig. S7, A versus C), the proportion of SNPs that display uncorrelated horizontal pleiotropic effects (fig. S7, A versus B), the proportion of SNPs that display correlated horizontal pleiotropic effects (fig. S7, A versus D), or how the correlated horizontal pleiotropic effects are created (fig. S8).
Simulations: Power comparison
We examined the power of different MR methods to detect nonzero causal effect. Because the same P value from different methods may correspond to different type I errors, we again computed power on the basis of an FDR of 0.05 instead of a nominal P value threshold to allow for fair comparison among methods. In the absence of both uncorrelated and correlated horizontal pleiotropic effects, MRAID, IVW-R, and RAPS all have high power across different scenarios. Among these three methods, MRAID is slightly more powerful than the other two when the instrumental effects are small or when the causal effect is small (Fig. 3, A and B), presumably due to the automated instrument selection procedure used in MRAID. MRAID is slightly less powerful than the other two when the instrumental effects are large and the causal effect is large (fig. S9), as the simple instrumental selection approaches used in the other methods can be effective in these lesser challenging settings. The performance of these three methods is generally followed by Robust, while Weighted mode, MRMix, and, to a lesser extent, CAUSE have low power.
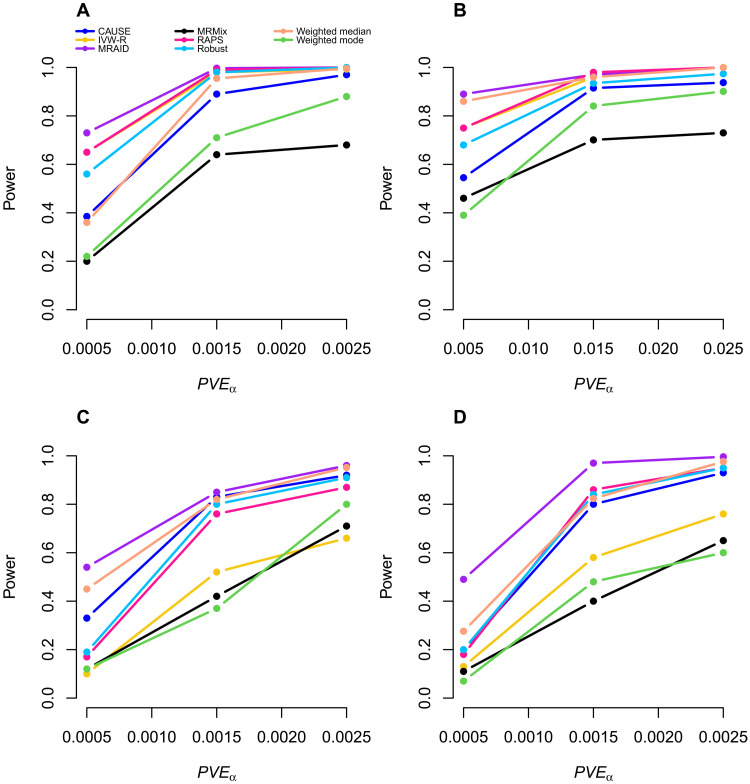
Fig. 3. Power of different MR methods in simulations.
Power (y axis) at an FDR of 0.05 to detect the causal effect is plotted against different causal effect size characterized by PVEα (x axis). Compared methods include CAUSE (blue), IVW-R (gold), MRAID (purple), MRMix (black), RAPS (deep pink), Robust (deep sky blue), Weighted median (light salmon), and Weighted mode (green). Four alternative simulation scenarios are examined. (A) Simulations in the absence of both correlated and uncorrelated horizontal pleiotropic effects. We simulated 100 instrumental SNPs with their effects size drawing from a normal distribution. (B) Simulations in the absence of both correlated and uncorrelated horizontal pleiotropic effects. We simulated 1000 instrumental SNPs with their effects size drawing from a BSLMM distribution with 1% SNPs having large effects and 99% SNPs having small effects. (C) Simulations in the absence of correlated horizontal pleiotropic effect but in the presence of uncorrelated horizontal pleiotropic effect (PVEu = 5%). We simulated 100 instrumental SNPs and set the proportion of instrumental SNPs having the uncorrelated horizontal pleiotropy effect to be 30%. (D) Simulations in the presence of both correlated (πc = 5%, ) and uncorrelated horizontal pleiotropic effects (PVEu = 5%). We simulated 100 causal instrumental SNPs and set the proportion of instrumental SNPs having the uncorrelated horizontal pleiotropy effect to be 20%.
We examined the influence of horizontal pleiotropy on the power of different methods. When horizontal pleiotropic effects are present but are uncorrelated with the instrumental effects, MRAID is more powerful than the other MR methods (Fig. 3C). The power gain brought by MRAID becomes more apparent with increasing horizontal pleiotropy, which is characterized by increased horizontal pleiotropic effect sizes and/or increased proportion of SNPs that display horizontal pleiotropic effects (fig. S10). The performance of MRAID is often followed by RAPS, Robust, CAUSE, IVW-R, and Weighted median, while MRMix and Weighted mode generally have low power (fig. S10). Among these methods, the performance of IVW-R is particularly sensitive to the horizontal pleiotropic effect sizes or the proportion of SNPs that display horizontal pleiotropic effects. When correlated horizontal pleiotropic effects are also present in addition to the uncorrelated horizontal pleiotropic effects, the power of MRAID remains higher than the other methods. The higher power of MRAID maintains regardless of the correlated horizontal pleiotropic effect sizes, the proportion of instrumental SNPs that display correlated horizontal pleiotropic effects (Fig. 3D and fig. S10D-F), or how the correlated horizontal pleiotropic effects are created (fig. S11). The power gain brought by MRAID is particularly apparent with increased proportion of instrumental SNPs that display uncorrelated horizontal pleiotropic effects (Fig. 3D versus fig. S10F and fig. S10, E versus D). The power of MRAID is close to an oracle MR approach that uses the actual set of instrumental SNPs for MR inference, especially when the casual effect size is large, supporting the effectiveness of the automatic instrument selection procedure in MRAID (fig. S12).
Next, we examined the ability of different MR methods in distinguishing the causal effect direction through reverse causality analysis. In particular, we tested the causal effect of the outcome on the exposure in the alternative simulations where the exposure had casual effect on the outcome but not vice versa. In the presence of horizontal pleiotropy, the SNP instruments obtained for the outcome in the reverse MR analysis would contain two sets of SNPs: a set of exposure SNP instruments that are indirectly associated with the outcome through the exposure and a set of SNPs that are directly associated with the outcome thought their horizontal pleiotropic effects on the outcome. Because the two sets of SNPs displayed heterogeneous effects on the exposure, we would fail to detect a nonzero causal effect of the outcome on the exposure. Therefore, the reverse causality analysis in the presence of horizontal pleiotropy effectively served as analysis on null simulations. We found that MRAID provides effective type I error control and calibrated P values in the reverse causality analysis across a range of simulation scenarios (figs. S13 and S14). In contrast, the type I error control of the other methods is highly dependent on the extent of the horizontal pleiotropy. Specifically, when a small proportion of exposure instrumental SNPs display horizontal pleiotropy on the outcome, most of the candidate instrumental SNPs for the outcome in the reverse causality analysis would not display horizontal pleiotropic effects on the exposure. In this case, both CAUSE and Weighted mode remain overly conservative, while IVW-R, MRMix, RAPS, and Robust yield slightly inflated P values (figs. S13, A and C, and S14, A and C). By contrast, when a large proportion of instrumental SNPs for the exposure display horizontal pleiotropic effects on the outcome, most of the candidate instrumental SNPs for the outcome in the reverse causality analysis would display horizontal pleiotropic effects on the exposure. In this case, MRMix, Robust, IVW-R, Weighted median, and RAPS all start to produce inflated P values (figs. S13B and S14B) as we have shown in the corresponding null scenarios. The P value inflation of these methods becomes more prominent with smaller horizontal pleiotropic effect sizes, where it becomes increasingly hard to select the second set of SNPs to serve as outcome instruments (figs. S13D and S14D). The comparison results hold when we force multiple causal SNPs to be in the same LD block (fig. S15).
MRAID also produces reasonably unbiased causal effect estimates under the null (fig. S16A) and under various alternatives (fig. S16, B to D) and produces reasonably well-estimated proportional estimates (fig. S17). In addition, MRAID is reasonably robust when the uncorrelated horizontal pleiotropic effects from the instrumental SNPs are either larger or smaller than that from the noninstrumental SNPs (fig. S18).
Real data applications
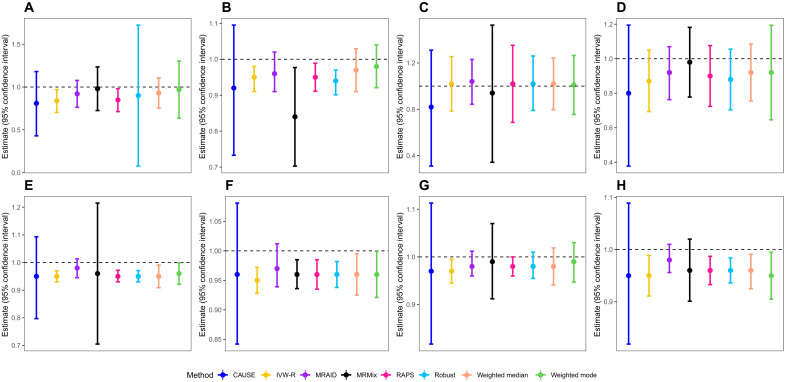
We applied MRAID and the other MR methods to analyze 38 lifestyle risk factors and 11 cardiovascular disease (CVD)-related traits in the U.K. Biobank (details in Materials and Methods). Specifically, we divided the U.K. Biobank data into two separate, equal-sized subsets, representing an exposure GWAS and an outcome GWAS. We performed two sets of analysis. First, we focused on the eight CVD-related traits and examined the causal effect of each trait in the exposure GWAS on the same trait in the outcome GWAS, effectively examining the causal effect of the trait on itself. The true causal effect in this analysis is nonzero and equals exactly to one, with the scatterplots displayed in fig. S19. We found that all methods were able to detect a nonzero causal effect for the trait on itself across all eight CVD-related traits (Fig. 4). However, only MRAID and CAUSE were able to produce 95% confidence intervals (CIs) that cover the true causal effects for all eight trait pairs, with CAUSE producing CIs that are 2.39 to 5.69 times larger than MRAID (Fig. 4). For example, in the high-density lipoprotein (HDL)–HDL analysis, MRAID (estimate = 0.98; 95% CI, 0.96 to 1.01), CAUSE (estimate = 0.95; 95% CI, 0.82 to 1.09), and MRMix (estimate = 0.96; 95% CI, 0.90 to 1.02) correctly inferred the causal effect, with MRAID providing the smallest CI (Fig. 4H). In contrast, the CIs from the other five methods did not cover the true causal effect of one. In the LDL-LDL analysis, MRAID (0.97; 0.94 to 1.01) and CAUSE (0.96; 0.84 to 1.08) correctly inferred the causal effect, with MRAID providing a smaller CI (Fig. 4F), while the CIs from the other six methods also did not cover the true causal effect of one. The results suggest that both MRAID and CAUSE can produce accurate causal effect estimates and calibrated CIs for the trait on itself analysis, with MRAID being more powerful than CAUSE. We applied similar analysis for investigating the causal effect of each of the four blood lipid traits in the global lipid genomic consortium (35) on the same trait in U.K. Biobank and found similar results (fig. S20). Certainly, while the above experiment is simple and straightforward and has been used for MR method comparison in the previous literature (6), we caution that some forms of bias such as weak instrument biases and/or winner’s curse may occur in this experiment just like in any other real data analysis experiments.
Fig. 4. Point estimates and 95% CIs from different MR methods in the trait on itself analysis in the real data.
Compared methods include CAUSE (blue), IVW-R (gold), MRAID (purple), MRMix (black), RAPS (deep pink), Robust (deep sky blue), Weighted median (light salmon), and Weighted mode (green). Analyzed trait pairs include SBP-SBP (A), BMI-BMI (B), DBP-DBP (C), pulse rate-pulse rate (D), TC-TC (E), LDL-LDL (F), TG-TG (G), and HDL-HDL (H). The horizontal black dashed line in each panel represents the true causal effect size of α = 1. Both MRAID and CAUSE can produce 95% CIs that cover the true causal effects of all trait pairs, with CAUSE producing much larger CIs than MRAID.
Next, we investigated the causal relationship between 38 lifestyle risk factors and 11 CVD-related traits. The association of lifestyle risk factors on CVD-related traits has been extensively documented (36, 37). However, it remains controversial on whether the detected associations are causal as some of the association effects were estimated to have different signs in different studies (38, 39). We performed both forward causality analysis examining the causal effects of lifestyle factors on CVD-related traits and reverse causality analysis examining the causal effects of CVD-related traits on lifestyle factors. The distribution of P values for the analyzed trait pairs from different methods are shown in Fig. 5A. Consistent with the simulations, we found that the P values from MRAID [genomic inflation factor (GIF) = 0.90)] and, to a lesser extent, MRMix (GIF = 0.78) are generally well behaved and slightly conservative across analyzed trait pairs, more so than the other methods (Fig. 5A). In addition, consistent with the simulations, we found that the P values from CAUSE are overly conservative (GIF = 0.12), while the P values from RAPS (GIF = 1.96), Weighted mode (GIF = 1.70), IVW-R (GIF = 2.12), Weighted median (GIF = 1.80), and Robust (GIF = 2.00) all show appreciable inflation (Fig. 5A). Only MRAID produces calibrated P values in the permutation analysis where we permuted the outcome trait (Fig. 5B).
Fig. 5. Quantile-quantile plot of −log10 P values from different MR methods on testing the causal relationship between lifestyle risk factors and CVD-related traits in U.K. Biobank.
Compared methods include CAUSE (blue), IVW-R (gold), MRAID (purple), MRMix (black), RAPS (deep pink), Robust (deep sky blue), Weighted median (light salmon), and Weighted mode (green). The results are shown for all 645 analyzed trait pairs (A) and the empirical null where we permuted the outcome 10 times in the MR analysis of lifestyle traits on CVD-related traits (B).
On the basis of a Bonferroni-corrected P value threshold (7.75 × 10−5), MRAID detected eight causal associations (table S2), all of which have strong biological support. For example, MRAID detected a negative causal effect of smoking on body mass index (BMI). The negative association between smoking and obesity has been well documented in observational studies (40, 41) and MR studies (42). Specifically, nicotine intake during smoking decreases resting metabolic rate (43, 44) and inhibits lipoprotein lipase activity and other kinase pathways to reduce lipolysis (41), all of which lead to a reduction in the net energy storage in adipose tissues and subsequent weight loss (45). Nicotine also activates acetylcholine receptors in the hypothalamus and subsequently anorexigenic neurons (46, 47), which leads to suppressed appetite and food intake. As another example, MRAID detected an effect of age started smoking in the former smokers on HDL, suggesting a negative effect of smoking behavior on HDL. Smoking behavior, in general, is well known to be causally associated with HDL (48). In particular, smoking can modify the activity of critical enzymes for lipid transport, lower lecithin-cholesterol acyltransferase activity, and alter cholesterol ester transfer protein and hepatic lipase activity, all of which can reduce HDL metabolism. In addition, smoking induces oxidative modifications that render HDL dysfunctional and deprive its atheroprotective properties (49, 50).
MRAID did not mistakenly detect many false causal associations that were detected by the other methods. A well-known example of a potential false causal association is the effect of smoking on blood pressure. A negative association between smoking and blood pressure has been observed in observational studies (37). However, multiple subsequent MR studies on large datasets did not support a causal relationship between the two traits (48, 51). The association between smoking and blood pressure in observational studies is likely confounded by factors that include, but not limited to, age, BMI, social class, salt intake, drinking habits, and unmeasured confounders (52). Consistent with these previous MR studies, MRAID did not detect a significant causal effect from any of the eight smoking related traits on either systolic blood pressure (SBP) or diastolic blood pressure (DBP). In contrast, almost all other methods falsely detected causal effects of some of the smoking-related traits on blood pressure. For example, the causal effect of the number of unsuccessful stop-smoking attempts on SBP is not detected by MRAID (P = 0.44), CAUSE (P = 0.01), nor Weighted mode (P = 1.3 × 10−4) but falsely identified by IVW-R (P = 1.4 × 10−6), Robust (P = 4.1 × 10−34), RAPS (P = 5.5 × 10−6), MRMix (P = 2.8 × 10−6), and Weighted median (P = 2.4 × 10−5). Similarly, the causal effect of age started smoking in former smokers on SBP is not detected by MRAID (P = 0.06) nor CAUSE (P = 1.3 × 10−3) but falsely detected by IVW-R (P = 7.8 × 10−5), Robust (P = 1.5 × 10−30), RAPS (P = 8.9 × 10−7), Weighted median (P = 1.0 × 10−6), Weighted mode (P = 1.7 × 10−6), and MRMix (P = 4.1 × 10−7). As another false example, BMI is unlikely to causally influence the time spent driving, at least not positively. MRAID (P = 0.01), along with MRMix (P = 0.12), CAUSE (P = 0.02), Weighted median (P = 0.04), and Weighted mode (P = 0.04), did not detect any causal effect of BMI on time spent driving. However, both IVW-R (P = 2.5 × 10−6) and RAPS (P = 3.1 × 10−5) detected a false-positive effect of BMI on time spent driving.
Last, we note that an important feature of MRAID is its ability to effectively decompose the SNP effects on the outcome into three distinct paths: One directly acts from SNPs to the outcome, one mediated through the exposure, and the other acts through a hidden confounding factor that influences both exposure and outcome. Consequently, MRAID can be used to estimate the proportion of SNPs in different categories, including the proportion of SNPs that are associated with the exposure among the genome-wide significant ones (πβ), the proportion of SNPs that exhibit correlated horizontal pleiotropy (πc), the proportion of SNPs that exhibit uncorrelated horizontal pleiotropy among the selected instruments (π1), and the proportion of SNPs that exhibit uncorrelated horizontal pleiotropy among the remaining candidate instruments (π0). In the real data applications, we estimated the mean of πβ, πc, π1, and π0 across the 645 analyzed trait pairs to be 14.6, 6.4, 16.4, and 5%, respectively (fig. S21). Note that these percentages were calculated on the basis of the number of candidate instruments; thus, a value of 14.6% corresponds to an average of 107 variants per trait. Additional analysis illustrated that the P values of MRAID remains consistent with each other regardless of the prior distribution of πβ (fig. S22). In addition, we estimated their means in the eight significant trait pairs to be 6.2, 5.7, 11.4, and 0.1%, respectively. The proportion of SNPs displaying correlated pleiotropy is also highly correlated with the proportion of SNPs displaying uncorrelated pleiotropy, with the latter generally being larger than the former (fig. S23). These proportion estimates support the widespread horizontal pleiotropy previously identified in complex trait analysis (25) and provide detailed quantifications on the extent to which the two types of horizontal pleiotropy influence MR analysis.
DISCUSSION
We have presented MRAID, a two-sample MR method that can automatically select suitable instruments from a candidate set of correlated SNPs and that can control for both correlated and uncorrelated horizontal pleiotropy in a likelihood-based inference framework. Overall, by automatically selecting instrumental SNPs and performing inference under a likelihood-based framework, MRAID yields calibrated P values across a wide range of scenarios and improves power of MR analysis over existing approaches. We have illustrated the benefits of MRAID through simulations and applications to complex trait analysis.
We have primarily focused on modeling quantitative traits with MRAID in the present study. For binary exposures and outcomes, one could treat them as continuous variables and directly applied MRAID for MR analysis. Treating binary exposures and outcomes as continuous variables can be justified by recognizing the linear model as a first-order Taylor approximation to a generalized linear model such as the logistic regression (53). However, this approximation is accurate only when the SNP effects on the exposure and outcome are relatively small. While similar approaches have been applied in many previous MR studies (54–56), we caution that the interpretation of the causal effect estimate can be challenging when the linear models are used to fit binary exposures and outcomes, especially when a two-stage inference procedure is used for MR analysis (57, 58). For example, when a binary exposure is a dichotomization of a continuous risk factor, the causal effect estimation through modeling the binary exposure without the underlying continuous risk factor may require additional modeling assumptions, even when the main MR assumptions are satisfied. In addition, modeling binary exposure without the underlying continuous risk factor can lead to violation of the exclusion restriction assumption, as the instruments can influence the outcome via the continuous risk factor even if the binary exposure does not change.
Therefore, extending MRAID to explicitly model data types beyond quantitative traits is important to ensure its wide applicability. Because MRAID builds upon a data generative model and performs inference on the SNP-exposure model and the SNP-outcome model jointly through a maximum likelihood–based framework, it can be naturally extended toward modeling binary outcome through a liability threshold model (59) and binary and other types of exposure or outcome data through a generalized linear model framework. To the best of our knowledge, the only likelihood-based MR method that accommodates both binary risk factors and outcome is IV-MVB (60). IV-MVB, however, requires individual-level data, applies to the one-sample analysis setting, and cannot easily handle multiple instruments in a computationally efficient fashion, especially for those that are correlated. Therefore, exploring the benefits of MRAID extensions toward modeling generalized data types while keeping computation in check will be an important direction for future research.
Another important future direction is to extend MRAID to incorporate SNP functional annotations. Specifically, we could model the probability of a SNP exhibiting instrumental effects as a function of a given set of SNP annotations through a logistic function, similar to what was used in many SNP fine-mapping methods (61–63). In addition, we could also model the probability of a SNP exhibiting horizontal pleiotropic effects as a function of its functional annotations through a logistic function. Because the biological function and importance of a SNP can be predicted in certain degree by its functional annotations, incorporating SNP functional annotations can potentially improve the performance of MRAID. Certainly, incorporating functional annotations would inevitably increase the number of parameters, making it challenging to carry out powerful MR inference given the small instrumental effects. Therefore, it would be important to incorporate informative functional annotations while mitigating the impact by the increased number of parameters to ensure optimal MR inference power.
MRAID is not without limitations. First, while MRAID performs automated selection on SNP instruments, this selection builds upon a sparsity inducing modeling assumption specified on the SNP effect sizes. The sparse modeling assumption contains multiple hyperparameters that rely on a sampling-based algorithm for inference. Accurate and robust inference of the hyperparameters will likely require at least a moderate number of candidate instruments. While the significance of the trait pairs evaluated by MRAID in our real data application does not appear to be dependent on the number of candidate instruments selected for the trait pair (fig. S24), we caution that MRAID may incur low power when the instrumental effect size is small and the number of candidate instruments is low, which can happen in GWAS with small sample sizes and for exposure traits with a nonpolygenic architecture. Second, MRAID primarily follows the approach of CAUSE to model correlated horizontal pleiotropy by introducing a single latent variable to serve as the confounder for both the exposure and the outcome. Because of its limitation in modeling only a single unobserved confounding factor, MRAID may not be fully effective in settings where multiple or other types of shared genetic components are present between the exposure and the outcome. Last, the summary statistics version of MRAID requires as input two LD matrices, one from the exposure GWAS and another from the outcome GWAS. In the present study, we have estimated both LD matrices using individual level data. In the absence of individual level data, both LD matrices may be estimated from a reference panel with the same genetic ancestry (e.g., from the 1000 Genomes Project). However, care needs to be taken when the exposure and outcome GWASs are carried out on two populations with distinct genetic ancestries or when the genetic ancestry of the reference panel does not match that of the GWAS (fig. S25).
MATERIALS AND METHODS
MRAID for individual level data
We provide an overview of our method here, with its inference and technical details provided in Supplementary Text and an illustrative diagram displayed in Fig. 1. Our goal is to estimate and test the causal effect of an exposure variable on an outcome variable in the two-sample MR setting where the exposure and outcome variables are measured in two separate GWASs with no sample overlap. We refer to the two separate GWASs as the exposure GWAS and the outcome GWAS, respectively. To set up the notations, we denote x as an n1-vector of the exposure variable measured on n1 individuals in the exposure GWAS. We denote y as an n2-vector of the outcome variable measured on n2 individuals in the outcome GWAS. We scale both x and y to have zero mean and unit SD. In the exposure GWAS, we perform an initial screening to select SNPs that are associated with the exposure variable with a marginal P value below the genome-wide significance threshold of 5 × 10−8. These SNPs are likely in LD with each other and are selected to serve as the initial set of candidate instruments. We denote Zx as the resulting n1 by p genotype matrix for the p-selected candidate instrumental SNPs in the exposure GWAS. We also denote Zy as an n2 by p genotype matrix for the same p candidate instrumental SNPs in the outcome GWAS. We scale each column of the two genotype matrices to have mean zero and an SD of one. We model the relationship among the exposure, outcome, and genotypes through the following three linear regressions
| (1) |
| (2) |
| (3) |
Above, Eq. 1 describes the relationship between the genotypes Zx and the exposure variable x in the exposure GWAS; Eq. 2 describes the relationship between the genotypes Zy and the unobserved exposure in the outcome GWAS; Eq. 3 describes the relationship among the genotypes Zy, the outcome y, and the unobserved exposure in the outcome GWAS; β is a p-vector of SNP effects on the exposure; both η0 and η1 are p-vectors of horizontal pleiotropy effects on the outcome; α is a scalar that represents the causal effect of the exposure on the outcome; εx is an n1-vector of residual error with each element independently and identically distributed from a normal distribution ; is an n2-vector of residual error with each element distributed from the same normal distribution ; and εy is an n2-vector of residual error with each element distributed from a normal distribution . We note that, while the above three equations are specified on the basis of two separate GWASs, they are connected to each other by the common parameter β. We carefully consider the modeling assumptions on the SNP effects on the exposure variable β and the horizontal pleiotropic effects η0 and η1 as follows.
The p SNPs included in the above model represent an initial set of candidate instruments. While all the candidate instruments are marginally associated with the exposure, most of them are unlikely the causal SNPs for the exposure variable. Instead, most candidate instruments likely represent tagging SNPs that are associated with the exposure variable due to LD with the truly causal ones underlying the exposure. Therefore, it would be beneficial to perform additional selections on the candidate instruments to identify SNPs that are causal for the exposure and treat them as the instruments to maximize the power of MR analysis. To do so, we borrow ideas from fine-mapping approaches developed in the research field of GWAS and specify a sparsity inducing modeling assumption on the SNP effects on the exposure (β) to perform automated instrument selection. In particular, we assume that , where δ0 is the Dirac function that represents a point mass at zero. That is, with probability 1 − πβ, the j-th SNP has zero effect on the exposure; while with probability πβ, the j-th SNP has a nonzero effect on the exposure, and its effect size follows a normal distribution with mean zero and variance , where the variance parameter determines the magnitude of the effect sizes. The sparse assumption on β allows us to select SNPs with nonzero effects on the exposure to serve as the instruments in the MR model.
In addition, the p SNPs included in the above model can also exhibit horizontal pleiotropic effects and influence the outcome variable through pathways other than the exposure. To control for the potential horizontal pleiotropic effects and improve causal effect inference, we introduce two sets of parameters, η0 and η1, to model horizontal pleiotropic effects. The two sets of parameters are placed separately for the two SNP groups—the group of selected instrumental SNPs and the group of unselected noninstrumental SNPs—which are categorized by the sparse modeling assumption on β. In particular, η1 represents the horizontal pleiotropic effects exhibited by the selected SNPs instruments with nonzero β, while η0 represents the horizontal pleiotropic effects exhibited by the unselected noninstrumental SNPs with zero β. Controlling for η1 can help mitigate the bias in causal effect estimation induced by horizontal pleiotropic effects from the instrumental SNPs, while controlling for η0 can reduce residual error variance in Eq. 3 and thus help improve the statistical efficiency of causal effect estimation.
To effectively control for the horizontal pleiotropic effects exhibited from both SNP groups, we specify separate modeling assumptions on η0 and η1. Specifically, for the selected SNP instruments, we assume that they can exhibit horizontal pleiotropic effects in two different ways: They can affect the outcome through a common confounder that is associated with both the exposure and outcome, and they can affect the outcome through paths independent of the exposure. For the first type of horizontal pleiotropy, we assume that each selected SNP instrument has a probability of πc to induce pleiotropy through the confounder. Following (8), we assume that the confounder effect on the outcome is ρ times its effect on the exposure. Consequently, the effect of the selected SNP instrument acted through the confounder on the outcome becomes ρβj if the SNP effect on the exposure is βj. Thus, our assumption on , which represents the first type of horizontal pleiotropy as a part of η1 for the j-th SNP, is , where I(·) is an indicator function that sets the horizontal pleiotropic effect to be ρβj. For the second type of horizontal pleiotropy, we assume that each selected SNP instrument has a probability of π1 to exhibit a horizontal pleiotropic effect on the outcome directly, bypassing the exposure. We use to represent the second type of horizontal pleiotropy as a part of η1 for the j-th SNP. Our assumption on is thus , where the variance determines the strength of the horizontal pleiotropic effect. Note that the first type of horizontal pleiotropic effects are correlated with the instrumental effects on the exposure due to the confounder, while the second type of horizontal pleiotropic effects are uncorrelated with the instrumental effects on the exposure. The total horizontal pleiotropy is the summation of the two, with . Certainly, because η1 are the horizontal pleiotropic effects for the selected SNP instruments, we have η1j = 0 if βj = 0. For the unselected noninstrumental SNPs with a zero βj, we assume that . That is, with probability π0, the noninstrumental SNPs display horizontal pleiotropic effects characterized by the same variance parameter . We use the same variance parameter for modeling the uncorrelated horizontal pleiotropic effects from both instrumental and noninstrumental SNPs because we often do not have enough number of SNPs to estimate two separate parameters accurately. Since η0 are the horizontal pleiotropic effects for the noninstruments, we also have η0j = 0 if βj ≠ 0.
The above parameterization of the horizontal pleiotropic effects is based on the selection of SNP instruments. An equivalent and alternative parametrization of the horizontal pleiotropic effects is to partition them into a correlated horizontal pleiotropic component ηc and an uncorrelated horizontal pleiotropic component ηu. Specifically, the correlated horizontal pleiotropy occurs only for the selected SNP instruments with ηcj∣βj ≠ 0~πcI(η1j = ρβj) + (1 − πc)δ0 and ηcj = 0 if βj = 0. The uncorrelated horizontal pleiotropy, on the other hand, occurs for both instrumental and noninstrumental SNPs with and . In other words, and .
Overall, the SNP effects on the outcome in our model are exhibited through three different paths: via the exposure on outcome causal effect α, via the correlated horizontal pleiotropic effects mediated by an unobserved confounder, and via the uncorrelated horizontal pleiotropic effects. SNPs in the model can exhibit none, one, or multiple types of these effects. Note that the SNP effects on the outcome through the causal effect and through the correlated horizontal pleiotropy are not distinguishable from each other unless we make further modeling assumptions. Here, following (8), we assume πc to be small. Thus, among the selected SNP instruments with nonzero effects on the exposure, only a fraction of them exhibit correlated horizontal pleiotropic effects on the outcome.
Our key parameter of interest is the causal effect α. The causal interpretation of α in a standard MR model requires the selected SNP instruments to satisfy three conditions: (i) Instruments are associated with the exposure (relevance condition); (ii) instruments are not associated with any other confounder that may be associated with both exposure and outcome (independence condition); and (iii) instruments only influence the outcome through the path of exposure (exclusion restriction condition). Our modeling assumption on β allows us to select SNPs to satisfy the relevance condition. Our modeling assumptions on η0 and η1 allow us to explicitly model the violation of the independence and exclusion restriction conditions. Therefore, our model effectively replaces the general conditions (ii) and (iii) with specific modeling assumptions on β, η0, and η1. In addition, through explicit modeling of the correlation between the instrument-exposure effects and instrument-outcome effects through ρ, our model no longer requires the Instrument Strength Independent of Direct Effect (InSIDE) assumption, which is sometimes referred to as the weak exclusion restriction condition (3). Consequently, the causal effect interpretation of α in our model only depends on the explicit assumptions made in the model.
We are interested in estimating the causal effect α and testing the null hypothesis H0: α = 0. Performing inference on α, however, is computationally challenging, as the likelihood defined on the basis of the above modeling assumptions is in a complicated form and involves integrations that cannot be obtained analytically. Here, we develop an approximate inference algorithm under the maximum likelihood framework to perform numerical integration of the likelihood and obtain an approximate P value for testing α. Our algorithm is based on the observation that the likelihood function of α can be expressed as a ratio between the posterior and the prior. Because the posterior of α is asymptotically normally distributed (64, 65), we can use Gibbs sampling to obtain posterior samples of α and use the sample mean and sample SD to summarize this posterior distribution. In addition, we can also specify a normal prior on α and obtain the prior mean and SD. Because the likelihood of α is expressed as the posterior divided by the prior and is itself asymptotically normally distributed (64, 65), we can rely on the method of moments to obtain the approximate maximum likelihood estimate and its based on the mean and SD from both the posterior and the prior. Afterward, we can construct an approximate Wald test statistic and obtain a P value for hypothesis testing. Details of the algorithm is provided in Supplementary Text. As a unique feature of our algorithm, we introduce a set of binary indicator variables to effectively explore the joint parameter space to alleviate the issue from the interdependence among the parameters η1, η0, and β (details in Supplementary Text). Note that, while our algorithm relies on Gibbs sampling, we do not perform a Bayesian analysis; rather, we treat the Gibbs sampling as a convenient and accurate numerical approximation tool to obtain the marginal likelihood of α, which is otherwise infeasible or inaccurate to obtain under various frequentist approaches.
We refer to our model and algorithm together as the two-sample MRAID. The MRAID part highlights the desirable feature of our model in automatically selecting instrumental variables from a set of candidate—ones that are in potentially high LD with each other. Compared with existing two-sample MR approaches, MRAID relies on a likelihood inference framework, is capable of modeling correlated instruments, performs automated instrument selection, controls for both correlated and uncorrelated horizontal pleiotropy, and is computationally scalable. MRAID is implemented in an R package freely available at www.xzlab.org/software.html.
MRAID for summary statistics
While we have described MRAID using individual-level data, MRAID can be extended to make use of only summary statistics. Details for the summary statistics version of MRAID are provided in Supplementary Text. Briefly, the summary statistics version of MRAID requires two types of input: the SNP marginal effect size estimates on the exposure and outcome and the SNP correlation matrices in the exposure and outcome GWASs. Both input types are obtained on the basis of standardized genotype data where the genotypes for each SNP have been standardized to have zero mean and unit SD. Here, we denote the p-vector of the SNP marginal effect size estimates on the exposure as and the corresponding vector of marginal effect size estimates on the outcome as . We denote the p by p SNP correlation matrix in the exposure GWAS as Σ1 and the corresponding matrix in the outcome GWAS as Σ2. Both Σ1 and Σ2 are positive semidefinite and can be estimated from the same LD reference panel (e.g., individuals with the same ancestry in the 1000 Genomes Project). The MRAID model for summary statistics can be constructed on the basis of the following two equations
| (4) |
| (5) |
where ex is a p-vector of residual error that follows a multivariate normal distribution and ey is a p-vector of residual error that follows another a multivariate normal distribution . A similar approximate inference algorithm under the maximum likelihood framework is developed for the summary version of MRAID.
Simulations
We performed realistic simulations to evaluate the performance of MRAID and compared it with seven existing MR methods. For simulations, we randomly selected 60,000 individuals from the U.K. Biobank (31). We split these individuals randomly into two equal-sized sets: one set with 30,000 individuals to serve as the exposure GWAS and another set with the remaining 30,000 individuals to serve as the outcome GWAS. For these individuals, we obtained their genotypes from 649,695 SNPs on chromosome 1 that are overlapped with the Kaiser Permanente/UCSF Genetic Epidemiology Research Study on Adult Health and Aging (GERA) study we used before (17), standardized each SNP to have mean zero and unit SD, and used the standardized genotypes to simulate the exposure and outcome. Specifically, in the exposure GWAS, we randomly selected K SNPs (K = 100 or 1000) to have nonzero effects on the exposure. We denoted the genotype matrix of the K SNPs as . We simulated the K SNP effect sizes on the exposure (β) from a normal distribution , where the scalarrepresents the proportion of variance in the exposure variable explained by these genetic effects. We summed the genetic effects across all K SNPs as . In addition, we simulated the residual errors εx from a normal distribution . We then summed the genetic effects and the residual errors to yield the simulated exposure variable x. In the outcome GWAS, we obtained the genotypes for the same K SNPs as and used the same β from the exposure GWAS to compute the genetic component underlying the outcome as . We set the causal effect α to be so that the proportion of variance in the outcome variable explained by the causal effect term () is PVEα. We randomly obtained πcK SNPs (rounded to an integer) from the K SNPs to exhibit correlated pleiotropy. We simulated the correlated pleiotropic effect sizes to be ρβ and set ρ so that the proportion of variance in the outcome variable explained by correlated pleiotropy is PVEc. In addition, we randomly obtained π1K SNPs (again rounded to an integer) from the K SNPs and randomly obtained 100 − π1K SNPs from the remaining noncausal SNPs to exhibit uncorrelated pleiotropy so that a total of 100 SNPs displayed uncorrelated pleiotropy. We simulated the uncorrelated horizontal pleiotropic effects for these 100 SNPs from a normal distribution and scaled them so that the proportion of phenotypic variance in the outcome explained by uncorrelated pleiotropy is PVEu. We simulated the residual errors εy from a normal distribution N(0,1 − PVEα − PVEc − PVEu). We summed the causal effect term, correlated and uncorrelated horizontal pleiotropic effects, and the residual errors to yield the simulated outcome y. We treated the causal SNPs as unknown and followed standard MR procedure to select SNPs to serve as the instrumental variables. To do so, we used the linear regression model implemented in genome-wide efficient mixed-model analysis (GEMMA) (66) to perform association analysis in the exposure GWAS and selected SNPs with a P value below 5 × 10−8 as the candidate instrumental variables for analysis. For the selected SNPs, we obtained their effect size estimates, SEs, and z scores to serve as the summary statistics input. We also denoted the standardized genotype matrices for the selected SNPs in the exposure and outcome GWASs as Zx and Zy, respectively. On the basis of the genotype matrices, we obtained the SNP correlation matrices as and to serve as input for MR model fitting.
In the simulations, we first examined a baseline simulation setting where we set , PVEα = 0, K = 100, πc = 0, PVEu = 0, and PVEc = 0. On top of the baseline setting, we varied one parameter at a time to examine the influence of various parameters on method performance. For , we set it to be either 5 or 10%. For β, in addition to simulating it from a normal distribution, we also simulated them from the Bayesian sparse linear mixed model (BSLMM) distribution (53). Specifically, we randomly selected either 1 or 10% of the K SNPs to have large effects, and these large-effect SNPs explain 20% of . We set the remaining SNPs to have small effects to explain the remaining . For K, we set it to be either 100 or 1000. For PVEα, we set it to be zero in the null simulations and examined different values in the alternative simulations. In the alternative simulations, we set PVEα to be 0.05, 0.15, or 0.25% when K = 100 and set it to be 0.5, 1.5, and 2.5% when K = 1000 to ensure sufficient power. For the uncorrelated horizontal pleiotropic effects, we set PVEu to be either 0, 2.5, or 5%. Under the null (PVEα = 0) in the absence of uncorrelated horizontal pleiotropy (PVEu = 0), we set K to be 100 or 1000. In the presence of uncorrelated horizontal pleiotropy, we set K to be 100 and set π1 to be either 0, 10, 20, or 30%. We also simulated the correlated pleiotropy effects and set πc to be either 5 or 10%, with ρ being or following the previous literature (8).
Note that MRAID used the same variance parameter for modeling the uncorrelated horizontal pleiotropic effects of both instrumental and noninstrumental SNPs, as the number of SNPs included in the model may not be sufficiently large for accurate inference of the two separate parameters. We conducted additional simulations to evaluate the robustness of MRAID against the violation of this assumption in the presence of horizontal pleiotropic effects (PVEu = 5%), with the proportion of instrumental SNPs having uncorrelated horizontal pleiotropy to be 20 and 30%, respectively. We set the variance parameter for generating the uncorrelated horizontal pleiotropic effects from the noninstrumental SNPs to be either three times or 1/3 of that from the instrumental SNPs.
For the above simulations, we examined the number of causal SNPs in each LD block. Specifically, we used LDetect (67) and followed its default settings to divide chromosome 1 into 133 independent LD blocks. We then examined the location of the randomly selected 100 causal SNPs in each simulation. We found that the mean proportion of LD blocks that contain at least one causal SNP across the 1000 simulation replicates is 51%. In the LD blocks that contain at least one causal SNPs, we found the number of causal SNPs ranges from one to seven. In particular, an average of 64% of LD blocks with at least one causal SNP contain exactly one causal SNP, and an average of 36% of LD blocks with at least one causal SNP contain more than one causal SNP. Therefore, it appears that multiple causal SNPs are presented in the same LD block in our simulations. For the SNPs that are in the same LD block, the mean of the absolute value of pairwise r2 is 0.76.
For null simulations, we performed 1000 simulation replicates in each scenario to examine type I error control. For power evaluation, we performed 100 alternative simulations along with 900 null simulations, with which we computed power on the basis of an FDR of 0.05. We then repeated this analysis five times and report the average power across these replicates. Note that we computed power on the basis of FDR instead of a nominal P value threshold to allow for fair comparison across methods, as the same P value from different methods may correspond to different type I errors.
Besides the above comprehensive simulations, we also conducted a set of simple simulations to help build the intuition of the benefits of MRAID brought by modeling multiple correlated SNPs. Specifically, we first used LDetect with the default settings to divide chromosome 1 into 133 approximately independent LD blocks (67). We randomly selected one LD block and randomly selected 10 SNPs in the LD block for simulations. Among the 10 SNPs, we randomly selected one SNP to be causal and applied different methods to perform MR analysis either with the causal SNP (i.e., 10 SNPs total) or without the causal SNPs (i.e., nine SNPs total). We also randomly selected two SNPs to be causal and performed MR analysis either with the causal SNPs (i.e., 10 SNPs total) or without the two causal SNPs (i.e., eight SNPs total). In addition, we randomly selected two neighborhood LD blocks on chromosome 1 and randomly selected 10 SNPs from each block for another set of simulations. We then carried out similar simulations, with one SNP in each LD block randomly selected to be causal and with the MR analysis performed either with or without the two causal SNPs. We examined both the type I error control and power in the absence of both correlated and uncorrelated horizontal pleiotropic effects. We set n1 = 30,000, n2 = 30,000, = 0.25%, PVEα = 0 (null simulation), or PVEα = 1% (power simulation) to examine the performance of MRAID and the MR method that uses only the lead variant.
Real data applications
We applied MRAID and other MR methods to detect causal associations between 38 lifestyle risk factors and 11 CVD-related traits in the U.K. Biobank. The U.K. Biobank data consist of 487,298 individuals and 92,693,895 imputed SNPs (31). We followed the same sample quality control procedure in Neale laboratory (https://github.com/Nealelab/UK_Biobank_GWAS/tree/master/imputed-v2-gwas) to retain a total of 337,129 individuals of European ancestry for analysis. We also filtered out SNPs with a Hardy Weinberg equilibrium (HWE) P < 10−7, a genotype call rate < 95%, or a minor allele frequency (MAF) < 0.001 to obtain a total of 13,876,958 SNPs for analysis. For the retained individuals, we obtained all lifestyle-related quantitative traits and CVD-related traits, removed those traits with a sample size less than 10,000, and focused on the remaining set of 38 lifestyle traits and 11 CVD-related traits for analysis. The 38 lifestyle traits include 8 physical activity traits, 12 alcohol intake traits, 10 diet traits (e.g., coffee and fruits), and 8 smoking-related traits. The 11 CVD-related traits include four pulse wave traits, two blood pressure traits (SBP and DBP), four lipid traits [LDL, HDL, total cholesterol (TC), and triglycerides (TG)], and BMI. Details of these traits are listed in table S3. Many of these lifestyle risk factors have been found to be associated with CVD-related traits in observational studies (68–70), although it remains unclear whether these associations represent causal relationship. For each trait in turn, we removed the effects of sex and top 10 genotype principal components to obtain the trait residuals, standardized the residuals to have a mean of zero and an SD of one, and used these scaled residuals for MR analysis.
To mimic the two-sample MR design, we randomly split the 337,129 individuals into two nonoverlap sets: an exposure GWAS set with 168,564 individuals and an outcome GWAS set with 168,565 individuals. The random data split strategy ensures sample homogeneity within each study and independence between studies and was extensively used in the previous MR literature (6, 71–73). We examined the 38 lifestyle traits in the exposure GWAS and examined the 11 CVD-related traits in the outcome GWAS. In both GWASs, we obtained summary statistics for each trait through linear regression implemented in GEMMA. When lifestyle traits in the exposure GWAS were treated as the exposure, we selected SNPs with a P value below 5 × 10−8 to serve as the candidate instruments for each exposure trait. Because almost all MR methods require at least two instrumental SNPs, and some methods can become unstable when the number of instrumental SNPs is too large, we removed exposure traits for which the number of candidate instruments is either below two or above 10,000. This way, we removed three traits with less than two candidate instruments and four traits with more than 10,000 candidate instruments. We paired the remaining 31 exposure lifestyle traits with 11 outcome CVD-related traits into 341 trait pairs. The mean number of significantly associated SNPs among the 31 traits is 286. When CVD-related traits in the outcome GWAS were treated as the exposure, we removed three traits with less than two candidate instruments, including pulse wave reflection index with no candidate SNP, pulse wave peak to peak time with one candidate SNP, and pulse wave arterial stiffness index with one candidate SNP. We still found that the remaining eight traits have a total of more than 10,000 candidate instruments. Therefore, for these remaining traits, we used a more stringent P value threshold of 1 × 10−15 to select SNP instruments and analyzed the resulting 304 trait pairs. The mean number of associated SNPs among the eight CVD-related traits is 2318. In total, we analyzed 645 trait pairs.
Compared methods
We compared the performance of MRAID with seven existing methods that include the following: (i) IVW-R, which is the random effects version of IVW. It obtains the causal effect estimate through weighting and combining the effect estimates from individual instruments. It relies on random effects to account for pleiotropy and effect estimate heterogeneity across instruments (74). (ii) Weighted mode, which is a mode version of IVW. It obtains the causal effect estimate as the mode, instead of the mean, of the effect estimates obtained from individual instruments (75). (iii) Robust, which is a robust version of IVW. It uses the MM-estimation procedure consisting of an initial S-estimate followed by an M-estimate (76) that is further combined with Tukey’s biweight loss function (77). (iv) Weighted median, which can provide the consistent estimator even when up to 50% of the information comes from invalid instrumental variables. We fitted methods (i) to (iv) using R package “MendelianRandomization” with default settings. (vi) RAPS, which is the MR-adjusted profile score method. It incorporates random effects and robust loss functions into the profile score to account for systematic and idiosyncratic pleiotropy (6). We fitted RAPS using R package “mr.raps.” (vi) MRMix, which relies on a mixture model to account for horizontal pleiotropic effects and their correlation with instrumental effect sizes (7). We fitted MRMix using R package “MRMix.” (vii) CAUSE, which identifies instrumental effect size patterns that are consistent with causal effects while accounting for correlated pleiotropy (8). We fitted CAUSE using R package “cause.” We compared MRAID with the above seven methods because CAUSE is one of the most recently developed methods; IVW-R, Robust, and RAPS all have been shown to have superior performance when the InSIDE assumption is satisfied, while MRMix and Weighted mode perform well even the InSIDE assumption is violated (8, 34). In both simulations and real data applications, we first obtained SNPs that achieve genome-wide significance level (P < 5 × 10−8) to serve as a candidate set of instrumental SNPs. We directly use this candidate set of instrumental SNPs for MRAID. Because all other MR methods require independent instrumental SNPs, we performed LD clumping on the candidate set of instrumental SNPs to select independent ones for analysis. LD clumping is performed using PLINK, where we set the LD r2 parameter to be 0.001. CAUSE also requires estimating some nuisance parameters in the model by using a random set of SNPs across the genome, and we did so by randomly selecting 100,000 SNPs following (8). Last, we explored an oracle approach in the power simulations where we knew the actual set of instrumental SNPs that affect the exposure variable. In the oracle approach, we obtained the actual set of instrumental SNPs, selected among them the independent ones via pruning, and used the selected set of SNPs to serve as instruments using the IVW-R method. The compared methods and their corresponding software are listed in table S4.
Last, in the simple illustrative simulations, we compared MRAID with the well-known Wald ratio estimator for MR analysis (33), which uses only a single instrument. The Wald ratio estimator for the causal effect is in the form of , where is the estimated single SNP effect on outcome and is the estimated single SNP effect on exposure. The corresponding test statistics is , where zx and zy are the z statistics from the exposure GWAS and outcome GWAS, respectively. The null distribution of T is approximated by a chi-square distribution with one degree of freedom.
Acknowledgments
Funding: Z.Y. was supported by the National Natural Science Foundation of China (82173624, 81872712), the Natural Science Foundation of Shandong Province (ZR2019ZD02), and the Young Scholars Program of Shandong University (2016WLJH23). X.Z. was supported by the University of Michigan. This study has been conducted using U.K. Biobank resource under application number 51470. U.K. Biobank was established by the Wellcome Trust medical charity, Medical Research Council, Department of Health, Scottish Government and the Northwest Regional Development Agency. It also has funding from the Welsh Assembly Government, British Heart Foundation, and Diabetes UK.
Author contributions: X.Z. conceived the idea. X.Z. and Z.Y. developed the methods. Z.Y. developed the software tool with assistance from L.L. Z.Y. performed simulations and real data analysis with assistance from L.L., P.G., R.Y., and F.X. X.Z. and Z.Y. wrote the manuscript with input from all other authors. All authors reviewed and approved the final manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: No data are generated in the present study. The U.K. Biobank data are from U.K. Biobank resource under application number 51470. The MRAID is implemented in the R package MRAID, freely available on GitHub (https://github.com/yuanzhongshang/MRAID) and Zenodo (10.5281/zenodo.5797172). All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Supplementary Text
Figs. S1 to S25
Tables S1 to S4
REFERENCES AND NOTES
- 1.Burgess S., Small D. S., Thompson S. G., A review of instrumental variable estimators for Mendelian randomization. Stat. Methods Med. Res. 26, 2333–2355 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Burgess S., Butterworth A., Thompson S. G., Mendelian randomization analysis with multiple genetic variants using summarized data. Genet. Epidemiol. 37, 658–665 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bowden J., Smith G. D., Burgess S., Mendelian randomization with invalid instruments: Effect estimation and bias detection through Egger regression. Int. J. Epidemiol. 44, 512–525 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bowden J., Davey Smith G., Haycock P. C., Burgess S., Consistent estimation in Mendelian randomization with some invalid instruments using a weighted median estimator. Genet. Epidemiol. 40, 304–314 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhao J., Ming J., Hu X., Chen G., Liu J., Yang C., Bayesian weighted Mendelian randomization for causal inference based on summary statistics. Bioinformatics 36, 1501–1508 (2020). [DOI] [PubMed] [Google Scholar]
- 6.Zhao Q., Wang J., Hemani G., Bowden J., Small D. S., Statistical inference in two-sample summary-data Mendelian randomization using robust adjusted profile score. Ann. Stat. 48, 1742–1769 (2020). [Google Scholar]
- 7.Qi G., Chatterjee N., Mendelian randomization analysis using mixture models for robust and efficient estimation of causal effects. Nat. Commun. 10, 1941 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Morrison J., Knoblauch N., Marcus J. H., Stephens M., He X., Mendelian randomization accounting for correlated and uncorrelated pleiotropic effects using genome-wide summary statistics. Nat. Genet. 52, 740–747 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hormozdiari F., Kostem E., Kang E. Y., Pasaniuc B., Eskin E., Identifying causal variants at loci with multiple signals of association. Genetics 198, 497–508 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wang G., Sarkar A., Carbonetto P., Stephens M., A simple new approach to variable selection in regression, with application to genetic fine mapping. J. R. Stat. Soc. B 82, 1273–1300 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen W., Larrabee B. R., Ovsyannikova I. G., Kennedy R. B., Haralambieva I. H., Poland G. A., Schaid D. J., Fine mapping causal variants with an approximate bayesian method using marginal test statistics. Genetics 200, 719–736 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Benner C., Spencer C. C. A., Havulinna A. S., Salomaa V., Ripatti S., Pirinen M., FINEMAP: Efficient variable selection using summary data from genome-wide association studies. Bioinformatics 32, 1493–1501 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yang J., Fritsche L. G., Zhou X., Abecasis G.; International Age-Related Macular Degeneration Genomics Consortium , A scalable bayesian method for integrating functional information in genome-wide association studies. Am. J. Hum. Genet. 101, 404–416 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Guan Y., Stephens M., Bayesian variable selection regression for genome-wide association studies and other large-scale problems. Ann. Appl. Stat. 5, 1780–1815 (2011). [Google Scholar]
- 15.Carbonetto P., Stephens M., Scalable variational inference for bayesian variable selection in regression, and its accuracy in genetic association studies. Bayesian Anal. 7, 73–108 (2012). [Google Scholar]
- 16.P. Carbonetto, X. Zhou, M. Stephens, varbvs: Fast variable selection for large-scale regression. arXiv: 1709.06597 (2017).
- 17.Yuan Z., Zhu H., Zeng P., Yang S., Sun S., Yang C., Liu J., Zhou X., Testing and controlling for horizontal pleiotropy with probabilistic Mendelian randomization in transcriptome-wide association studies. Nat. Commun. 11, 3861 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhu H., Zhou X., Statistical methods for SNP heritability estimation and partition: A review. Comput. Struct. Biotechnol. J. 18, 1557–1568 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Burgess S., Dudbridge F., Thompson S. G., Combining information on multiple instrumental variables in Mendelian randomization: Comparison of allele score and summarized data methods. Stat. Med. 35, 1880–1906 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Burgess S., Thompson S. G., Bias in causal estimates from Mendelian randomization studies with weak instruments. Stat. Med. 30, 1312–1323 (2011). [DOI] [PubMed] [Google Scholar]
- 21.Zeng P., Zhou X., Huang S., Prediction of gene expression with cis-SNPs using mixed models and regularization methods. BMC Genomics 18, 368 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gusev A., Ko A., Shi H., Bhatia G., Chung W., Penninx B. W., Jansen R., de Geus E. J., Boomsma D. I., Wright F. A., Sullivan P. F., Nikkola E., Alvarez M., Civelek M., Lusis A. J., Lehtimäki T., Raitoharju E., Kähönen M., Seppälä I., Raitakari O. T., Kuusisto J., Laakso M., Price A. L., Pajukanta P., Pasaniuc B., Integrative approaches for large-scale transcriptome-wide association studies. Nat. Genet. 48, 245–252 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zeng P., Zhou X., Non-parametric genetic prediction of complex traits with latent Dirichlet process regression models. Nat. Commun. 8, 456 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liu L., Zeng P., Xue F., Yuan Z., Zhou X., Multi-trait transcriptome-wide association studies with probabilistic Mendelian randomization. Am. J. Hum. Genet. 108, 240–256 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Verbanck M., Chen C. Y., Neale B., Do R., Detection of widespread horizontal pleiotropy in causal relationships inferred from Mendelian randomization between complex traits and diseases. Nat. Genet. 50, 693–698 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Johnson A. M., Olefsky J. M., The origins and drivers of insulin resistance. Cell 152, 673–684 (2013). [DOI] [PubMed] [Google Scholar]
- 27.Garvey W. T., Kwon S., Zheng D., Shaughnessy S., Wallace P., Hutto A., Pugh K., Jenkins A. J., Klein R. L., Liao Y., Effects of insulin resistance and type 2 diabetes on lipoprotein subclass particle size and concentration determined by nuclear magnetic resonance. Diabetes 52, 453–462 (2003). [DOI] [PubMed] [Google Scholar]
- 28.Zhu Z., Zheng Z., Zhang F., Wu Y., Trzaskowski M., Maier R., Robinson M. R., McGrath J. J., Visscher P. M., Wray N. R., Yang J., Causal associations between risk factors and common diseases inferred from GWAS summary data. Nat. Commun. 9, 224 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zeng P., Wang T., Zheng J., Zhou X., Causal association of type 2 diabetes with amyotrophic lateral sclerosis: New evidence from Mendelian randomization using GWAS summary statistics. BMC Med. 17, 225 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zeng P., Zhou X., Causal effects of blood lipids on amyotrophic lateral sclerosis: A Mendelian randomization study. Hum. Mol. Genet. 28, 688–697 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bycroft C., Freeman C., Petkova D., Band G., Elliott L. T., Sharp K., Motyer A., Vukcevic D., Delaneau O., O’Connell J., Cortes A., Welsh S., Young A., Effingham M., Vean G. M., Leslie S., Allen N., Donnelly P., Marchini J., The UK Biobank resource with deep phenotyping and genomic data. Nature 562, 203–209 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schaid D. J., Chen W. N., Larson N. B., From genome-wide associations to candidate causal variants by statistical fine-mapping. Nat. Rev. Genet. 19, 491–504 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhu Z., Zhang F., Hu H., Bakshi A., Robinson M. R., Powell J. E., Montgomery G. W., Goddard M. E., Wray N. R., Visscher P. M., Yang J., Integration of summary data from GWAS and eQTL studies predicts complex trait gene targets. Nat. Genet. 48, 481–487 (2016). [DOI] [PubMed] [Google Scholar]
- 34.Qi G., Chatterjee N., A comprehensive evaluation of methods for Mendelian randomization using realistic simulations and an analysis of 38 biomarkers for risk of type 2 diabetes. Int. J. Epidemiol. 50, 1335–1349 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Willer C. J., Schmidt E. M., Sengupta S., Peloso G. M., Gustafsson S., Kanoni S., Ganna A., Chen J., Buchkovich M. L., Mora S., Beckmann J. S., Bragg-Gresham J. L., Chang H. Y., Demirkan A., Den Hertog H. M., Do R., Donnelly L. A., Ehret G. B., Esko T., Feitosa M. F., Ferreira T., Fischer K., Fontanillas P., Fraser R. M., Freitag D. F., Gurdasani D., Heikkila K., Hypponen E., Isaacs A., Jackson A. U., Johansson A., Johnson T., Kaakinen M., Kettunen J., Kleber M. E., Li X., Luan J., Lyytikainen L. P., Magnusson P. K. E., Mangino M., Mihailov E., Montasser M. E., Muller-Nurasyid M., Nolte I. M., O’Connell J. R., Palmer C. D., Perola M., Petersen A. K., Sanna S., Saxena R., Service S. K., Shah S., Shungin D., Sidore C., Song C., Strawbridge R. J., Surakka I., Tanaka T., Teslovich T. M., Thorleifsson G., Van den Herik E. G., Voight B. F., Volcik K. A., Waite L. L., Wong A., Wu Y., Zhang W., Absher D., Asiki G., Barroso I., Been L. F., Bolton J. L., Bonnycastle L. L., Brambilla P., Burnett M. S., Cesana G., Dimitriou M., Doney A. S. F., Doring A., Elliott P., Epstein S. E., Eyjolfsson G. I., Gigante B., Goodarzi M. O., Grallert H., Gravito M. L., Groves C. J., Hallmans G., Hartikainen A. L., Hayward C., Hernandez D., Hicks A. A., Holm H., Hung Y. J., Illig T., Jones M. R., Kaleebu P., Kastelein J. J. P., Khaw K. T., Kim E., Klopp N., Komulainen P., Kumari M., Langenberg C., Lehtimaki T., Lin S. Y., Lindstrom J., Loos R. J. F., Mach F., McArdle W. L., Meisinger C., Mitchell B. D., Muller G., Nagaraja R., Narisu N., Nieminen T. V. M., Nsubuga R. N., Olafsson I., Ong K. K., Palotie A., Papamarkou T., Pomilla C., Pouta A., Rader D. J., Reilly M. P., Ridker P. M., Rivadeneira F., Rudan I., Ruokonen A., Samani N., Scharnagl H., Seeley J., Silander K., Stancakova A., Stirrups K., Swift A. J., Tiret L., Uitterlinden A. G., van Pelt L. J., Vedantam S., Wainwright N., Wijmenga C., Wild S. H., Willemsen G., Wilsgaard T., Wilson J. F., Young E. H., Zhao J. H., Adair L. S., Arveiler D., Assimes T. L., Bandinelli S., Bennett F., Bochud M., Boehm B. O., Boomsma D. I., Borecki I. B., Bornstein S. R., Bovet P., Burnier M., Campbell H., Chakravarti A., Chambers J. C., Chen Y. I., Collins F. S., Cooper R. S., Danesh J., Dedoussis G., de Faire U., Feranil A. B., Ferrieres J., Ferrucci L., Freimer N. B., Gieger C., Groop L. C., Gudnason V., Gyllensten U., Hamsten A., Harris T. B., Hingorani A., Hirschhorn J. N., Hofman A., Hovingh G. K., Hsiung C. A., Humphries S. E., Hunt S. C., Hveem K., Iribarren C., Jarvelin M. R., Jula A., Kahonen M., Kaprio J., Kesaniemi A., Kivimaki M., Kooner J. S., Koudstaal P. J., Krauss R. M., Kuh D., Kuusisto J., Kyvik K. O., Laakso M., Lakka T. A., Lind L., Lindgren C. M., Martin N. G., Marz W., McCarthy M. I., McKenzie C. A., Meneton P., Metspalu A., Moilanen L., Morris A. D., Munroe P. B., Njolstad I., Pedersen N. L., Power C., Pramstaller P. P., Price J. F., Psaty B. M., Quertermous T., Rauramaa R., Saleheen D., Salomaa V., Sanghera D. K., Saramies J., Schwarz P. E. H., Sheu W. H., Shuldiner A. R., Siegbahn A., Spector T. D., Stefansson K., Strachan D. P., Tayo B. O., Tremoli E., Tuomilehto J., Uusitupa M., van Duijn C. M., Vollenweider P., Wallentin L., Wareham N. J., Whitfield J. B., Wolffenbuttel B. H. R., Ordovas J. M., Boerwinkle E., Palmer C. N. A., Thorsteinsdottir U., Chasman D. I., Rotter J. I., Franks P. W., Ripatti S., Cupples L. A., Sandhu M. S., Rich S. S., Boehnke M., Deloukas P., Kathiresan S., Mohlke K. L., Ingelsson E., Abecasis G. R.; Global Lipids Genetics Consortium , Discovery and refinement of loci associated with lipid levels. Nat. Genet. 45, 1274–1283 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mozaffarian D., Wilson P. W., Kannel W. B., Beyond established and novel risk factors: Lifestyle risk factors for cardiovascular disease. Circulation 117, 3031–3038 (2008). [DOI] [PubMed] [Google Scholar]
- 37.Brummett B. H., Babyak M. A., Siegler I. C., Shanahan M., Harris K. M., Elder G. H., Williams R. B., Systolic blood pressure, socioeconomic status, and biobehavioral risk factors in a nationally representative US young adult sample. Hypertension 58, 161–166 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Barker A. R., Gracia-Marco L., Ruiz J. R., Castillo M. J., Aparicio-Ugarriza R., Gonzalez-Gross M., Kafatos A., Androutsos O., Polito A., Molnar D., Widhalm K., Moreno L. A., Physical activity, sedentary time, TV viewing, physical fitness and cardiovascular disease risk in adolescents: The HELENA study. Int. J. Cardiol. 254, 303–309 (2018). [DOI] [PubMed] [Google Scholar]
- 39.Hadgraft N. T., Winkler E., Climie R. E., Grace M. S., Romero L., Owen N., Dunstan D., Healy G., Dempsey P. C., Effects of sedentary behaviour interventions on biomarkers of cardiometabolic risk in adults: Systematic review with meta-analyses. Br. J. Sports Med. 55, 144–154 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dare S., Mackay D. F., Pell J. P., Relationship between smoking and obesity: A cross-sectional study of 499,504 middle-aged adults in the UK general population. PLOS ONE 10, e0123579 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yuan Z., Ji J., Zhang T., Liu Y., Zhang X., Chen W., Xue F., A novel chi-square statistic for detecting group differences between pathways in systems epidemiology. Stat. Med. 35, 5512–5524 (2016). [DOI] [PubMed] [Google Scholar]
- 42.Winslow U. C., Rode L., Nordestgaard B. G., High tobacco consumption lowers body weight: A Mendelian randomization study of the Copenhagen General Population Study. Int. J. Epidemiol. 44, 540–550 (2015). [DOI] [PubMed] [Google Scholar]
- 43.Hofstetter A., Schutz Y., Jequier E., Wahren J., Increased 24-hour energy expenditure in cigarette smokers. N. Engl. J. Med. 314, 79–82 (1986). [DOI] [PubMed] [Google Scholar]
- 44.Moffatt R. J., Owens S. G., Cessation from cigarette smoking: Changes in body weight, body composition, resting metabolism, and energy consumption. Metabolism 40, 465–470 (1991). [DOI] [PubMed] [Google Scholar]
- 45.Ferrara C. M., Kumar M., Nicklas B., McCrone S., Goldberg A. P., Weight gain and adipose tissue metabolism after smoking cessation in women. Int. J. Obes. 25, 1322–1326 (2001). [DOI] [PubMed] [Google Scholar]
- 46.Jo Y. H., Talmage D. A., Role L. W., Nicotinic receptor-mediated effects on appetite and food intake. J. Neurosci. 53, 618–632 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mineur Y. S., Abizaid A., Rao Y., Salas R., DiLeone R. J., Gundisch D., Diano S., De Biasi M., Horvath T. L., Gao X. B., Picciotto M. R., Nicotine decreases food intake through activation of POMC neurons. Science 332, 1330–1332 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rosoff D. B., Davey Smith G., Mehta N., Clarke T. K., Lohoff F. W., Evaluating the relationship between alcohol consumption, tobacco use, and cardiovascular disease: A multivariable Mendelian randomization study. PLoS Med. 17, e1003410 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.He B. M., Zhao S. P., Peng Z. Y., Effects of cigarette smoking on HDL quantity and function: Implications for atherosclerosis. J. Cell. Biochem. 114, 2431–2436 (2013). [DOI] [PubMed] [Google Scholar]
- 50.Gepner A. D., Piper M. E., Johnson H. M., Fiore M. C., Baker T. B., Stein J. H., Effects of smoking and smoking cessation on lipids and lipoproteins: Outcomes from a randomized clinical trial. Am. Heart J. 161, 145–151 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Linneberg A., Jacobsen R. K., Skaaby T., Taylor A. E., Fluharty M. E., Jeppesen J. L., Bjorngaard J. H., Asvold B. O., Gabrielsen M. E., Campbell A., Marioni R. E., Kumari M., Marques-Vidal P., Kaakinen M., Cavadino A., Postmus I., Ahluwalia T. S., Wannamethee S. G., Lahti J., Raikkonen K., Palotie A., Wong A., Dalgard C., Ford I., Ben-Shlomo Y., Christiansen L., Kyvik K. O., Kuh D., Eriksson J. G., Whincup P. H., Mbarek H., de Geus E. J., Vink J. M., Boomsma D. I., Smith G. D., Lawlor D. A., Kisialiou A., McConnachie A., Padmanabhan S., Jukema J. W., Power C., Hypponen E., Preisig M., Waeber G., Vollenweider P., Korhonen T., Laatikainen T., Salomaa V., Kaprio J., Kivimaki M., Smith B. H., Hayward C., Sorensen T. I., Thuesen B. H., Sattar N., Morris R. W., Romundstad P. R., Munafo M. R., Jarvelin M. R., Husemoen L. L. N., Effect of smoking on blood pressure and resting heart rate: A Mendelian randomization meta-analysis in the CARTA Consortium. Circ. Cardiovasc. Genet. 8, 832–841 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Luehrs R. E., Zhang D., Pierce G. L., Jacobs D. R. Jr., Kalhan R., Whitaker K. M., Cigarette smoking and longitudinal associations with blood pressure: The CARDIA Study. J. Am. Heart Assoc. 10, e019566 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zhou X., Carbonetto P., Stephens M., Polygenic modeling with bayesian sparse linear mixed models. PLOS Genet. 9, e1003264 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Richardson T. G., Sanderson E., Elsworth B., Tilling K., Davey Smith G., Use of genetic variation to separate the effects of early and later life adiposity on disease risk: Mendelian randomisation study. BMJ 369, m1203 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Vaucher J., Keating B. J., Lasserre A. M., Gan W., Lyall D. M., Ward J., Smith D. J., Pell J. P., Sattar N., Pare G., Holmes M. V., Cannabis use and risk of schizophrenia: A Mendelian randomization study. Mol. Psychiatry 23, 1287–1292 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gormley M., Dudding T., Sanderson E., Martin R. M., Thomas S., Tyrrell J., Ness A. R., Brennan P., Munafo M., Pring M., Boccia S., Olshan A. F., Diergaarde B., Hung R. J., Liu G., Davey Smith G., Richmond R. C., A multivariable Mendelian randomization analysis investigating smoking and alcohol consumption in oral and oropharyngeal cancer. Nat. Commun. 11, 6071 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Burgess S., Labrecque J. A., Mendelian randomization with a binary exposure variable: Interpretation and presentation of causal estimates. Eur. J. Epidemiol. 33, 947–952 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Baiocchi M., Cheng J., Small D. S., Instrumental variable methods for causal inference. Stat. Med. 33, 2297–2340 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.M. Lynch, B. Walsh, Genetics and Analysis of Quantitative Traits (Sinauer Associates, 1998). [Google Scholar]
- 60.Allman P. H., Aban I., Long D. M., Bridges S. L. Jr., Srinivasasainagendra V., MacKenzie T., Cutter G., Tiwari H. K., A novel Mendelian randomization method with binary risk factor and outcome. Genet. Epidemiol. 45, 549–560 (2021). [DOI] [PubMed] [Google Scholar]
- 61.Kichaev G., Yang W. Y., Lindstrom S., Hormozdiari F., Eskin E., Price A. L., Kraft P., Pasaniuc B., Integrating functional data to prioritize causal variants in statistical fine-mapping studies. PLOS Genet. 10, e1004722 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Kichaev G., Pasaniuc B., Leveraging functional-annotation data in trans-ethnic fine-mapping studies. Am. J. Hum. Genet. 97, 260–271 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kichaev G., Roytman M., Johnson R., Eskin E., Lindstrom S., Kraft P., Pasaniuc B., Improved methods for multi-trait fine mapping of pleiotropic risk loci. Bioinformatics 33, 248–255 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Lea A. J., Tung J., Zhou X., A flexible, efficient binomial mixed model for identifying differential DNA methylation in bisulfite sequencing data. PLoS Genet. 11, e1005650 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Sun S., Hood M., Scott L., Peng Q., Mukherjee S., Tung J., Zhou X., Differential expression analysis for RNAseq using Poisson mixed models. Nucleic Acids Res. 45, e106 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Zhou X., Stephens M., Genome-wide efficient mixed-model analysis for association studies. Nat. Genet. 44, 821–824 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Berisa T., Pickrell J. K., Approximately independent linkage disequilibrium blocks in human populations. Bioinformatics 32, 283–285 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Stampfer M. J., Hu F. B., Manson J. E., Rimm E. B., Willett W. C., Primary prevention of coronary heart disease in women through diet and lifestyle. N. Engl. J. Med. 343, 16–22 (2000). [DOI] [PubMed] [Google Scholar]
- 69.Odegaard A. O., Koh W. P., Gross M. D., Yuan J. M., Pereira M. A., Combined lifestyle factors and cardiovascular disease mortality in Chinese men and women: The Singapore Chinese health study. Circulation 124, 2847–2854 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Huxley R. R., Woodward M., Cigarette smoking as a risk factor for coronary heart disease in women compared with men: A systematic review and meta-analysis of prospective cohort studies. Lancet 378, 1297–1305 (2011). [DOI] [PubMed] [Google Scholar]
- 71.Mountjoy E., Davies N. M., Plotnikov D., Smith G. D., Rodriguez S., Williams C. E., Guggenheim J. A., Atan D., Education and myopia: Assessing the direction of causality by mendelian randomisation. BMJ 361, k2022 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Henry A., Katsoulis M., Masi S., Fatemifar G., Denaxas S., Acosta D., Garfield V., Dale C. E., The relationship between sleep duration, cognition and dementia: A Mendelian randomization study. Int. J. Epidemiol. 48, 849–860 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Zhao Q., Wang J., Spiller W., Bowden J., Small D. S., Two-sample instrumental variable analyses using heterogeneous samples. Stat. Sci. 34, 317–333 (2019). [Google Scholar]
- 74.Bowden J., Del Greco M. F., Minelli C., Davey Smith G., Sheehan N., Thompson J., A framework for the investigation of pleiotropy in two-sample summary data Mendelian randomization. Stat. Med. 36, 1783–1802 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Hartwig F. P., Davey Smith G., Bowden J., Robust inference in summary data Mendelian randomization via the zero modal pleiotropy assumption. Int. J. Epidemiol. 46, 1985–1998 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Koller M., Stahel W. A. J. C. S., Analysis D., Sharpening wald-type inference in robust regression for small samples. Comput. Stat. Data Anal. 55, 2504–2515 (2011). [Google Scholar]
- 77.S. Burgess, J. Bowden, F. Dudbridge, S. G. Thompson, Robust instrumental variable methods using multiple candidate instruments with application to Mendelian randomization. arXiv:1606.03729 (2016).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S25
Tables S1 to S4