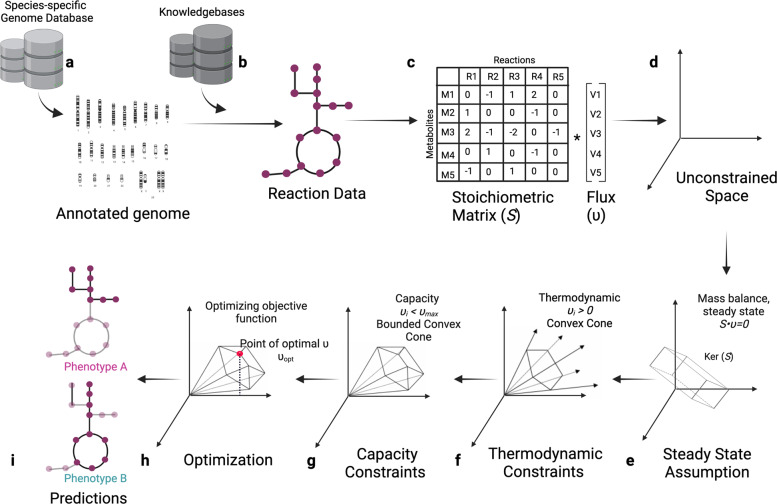
Fig. 2.

Schematic overview of a constraint-based modeling approach to study metabolism. a Annotated genes from a species of interest are combined with metabolic knowledge bases to generate a draft for the metabolic reactions available to a cell. b This draft is refined based on existing knowledge bases, and computational gap filling [104–106] is applied to ensure desired properties, such as the ability to generate ATP from a given substrate. c The product of this phase is a stoichiometric matrix (S) wherein entries are the stoichiometric coefficient of a particular metabolite (row) in a particular reaction (column). Reactions that have only negative or positive entries are exchange reactions that allow metabolite intake into and secretion out of the system (e.g., R5 in the illustrated matrix). d, e Imposing the assumptions of mass balance and of biochemical steady-state (i.e., constant metabolite concentrations) leads to a feasible space of metabolic flux distributions v (mathematically, this is the kernel of the stoichiometric matrix, namely, the solution space of S · ν = 0). The addition of (f) thermodynamic and (g) capacity constraints further restrict the feasible flux distribution space into a convex cone and bounded convex cone, respectively [71, 123, 124]. h The optimization of objective functions is used to detect mechanistically relevant flux distributions (i.e., the assignment of predicted flux for each reaction). The optimization of the pertinent objective (e.g., synthesis of biomass molecules) allows finding the vertices of the convex cone (namely, specific flux distributions) of interest, although the system is often underconstrained, and as a result, the solution to the optimization problem is nonunique. i The final outcome is predicted flux distributions, namely, the assignment of flux values to each reaction, that achieve the optimum of the stated objective, subject to the stated constraints. Often, the optimization function and/or constraints are informed by empirical high-throughput data, such as gene expression of different phenotypes/cells as denoted in the figure.