Validity and Reliability Analysis of the PlotDigitizer Software Program for Data Extraction from Single-Case Graphs

Abstract

Access to raw data of graphs presented in original articles to calculate the effect size of single-case research is a challenge for researchers conducting studies such as meta-analysis. Researchers typically use data extraction software programs to extract raw data from the graphs in articles. In this study, we aimed to analyze the validity and reliability of the PlotDigitizer software program, which is widely used in literature and an alternative to other data extraction programs, on computers with different operating systems. We performed the digitization of 6.846 data points on three different computers using 15 hypothetical graphs with 20 data series and 186 graphs with 242 data series from 29 published articles to accomplish the goal. Besides, using the values we digitized, we recalculated the 23 effect sizes presented in the original articles for validity analysis. Based on our sampling, we calculated intercoder and intracoder Pearson correlation coefficients. The results showed that PlotDigitizer could be an alternative to other programs as it is free and can run on many current and outdated systems, and it is valid and reliable as it is nearly perfect. Based on the obtained results and considering the data extraction process, we presented various recommendations for the researchers that will use the PlotDigitizer program for the quantitative analysis of single-case graphs.

Introduction

Single-case experimental designs (SCEDs), which are increasingly used in the fields of education and psychology, are unique methods that allow questioning the causal and functional relation between dependent and independent variables among the participants or between conditions (Kratochwill et al., 2010; Maggin et al., 2017; Maggin & Odom, 2014; Tekin-Iftar, 2018). The research on SCEDs can be conducted with a single participant or through the individual evaluation of multiple participants’ performances, and these performances are shown with graphical data.

In the studies conducted on SCEDs, repeated measurements are performed under standard conditions, and the changes between the baseline and intervention phases are visually analyzed using graphical data (Kennedy, 2005; Riley-Tillman & Burns, 2020; Tekin-Iftar, 2018). However, it is argued that visual analysis is invalid and unreliable owing to its subjectivity, and therefore, it is recommended to calculate effect sizes for SCEDs studies (Kratochwill et al., 2014; Manolov & Vannest, 2019; Shadish et al., 2015). On the other hand, it is not yet a common practice to report the effect sizes of interventions in single-case research (Busse et al., 2015; Olive & Franco, 2008). Furthermore, there are numerous methods for calculating the effect size on SCEDs. This leads to the absence of a common method used in the studies of SCEDs to report the effect size. Besides, researchers conducting meta-analysis studies may use other than the effect-size methods presented in articles to combine and interpret effect sizes of interventions. Therefore, regardless of whether the effect size is reported in the single-case studies, the need arises to reanalyze the studies’ data for the researchers performing studies such as meta-analysis (Shadish et al., 2009).

It is rare to present raw data along with graphical data in the research articles of SCEDs due to the page restrictions of journals or disrupting the reader-friendly flow. Instead, some researchers that conduct interventions prefer to report the mean values of baseline and intervention phases. The original mean values presented in articles could be useful for the researchers who will perform the effect-size calculations using the methods based on mean values (e.g., performance criteria-based effect size, standardized mean difference, and mean baseline reduction). However, when specific studies focusing on one variable are reviewed, it is seen that the number of studies reporting the mean values is relatively low (e.g., Rakap et al., 2016; Shadish et al., 2009). Furthermore, raw data of single-case graphs are needed to enable analysis with different effect-size methods (e.g., Tau-U, IRD). Therefore, using valid and reliable data extraction software programs becomes necessary for researchers who calculate effect sizes on single-case studies.

Software Programs for Extracting Raw Data from Graphs

There are some paid or free programs that are compatible with operating systems such as macOS or Windows for extracting raw data. Different researchers examined the validity and reliability of these software programs for only single-case graphs such as UnGraph (Moeyaert et al., 2016; Rakap et al., 2016; Shadish et al., 2009), GraphClick (Boyle et al., 2013; Flower et al., 2016; Rakap et al., 2016), Digitizelt (Rakap et al., 2016), DataThief (Flower et al., 2016; Moeyaert et al., 2016), and XYit (Moeyaert et al., 2016) or the web-based program Webplotdigitzer (Drevon et al., 2017; Moeyaert et al., 2016). Table 1 presents descriptive information and the validity and reliability coefficients of these programs.

Table 1.

Data digitization programs and validity and reliability findings

Name of the Program	Manufacturer	Price	Supported Operating System	Validity and Reliability Study	Data Digitized for Reliability	Reliability Correlation/Percentage	Method Followed in Validity Analysis	Data Used in Validity	Validity Correlation
UnGraph	Biosoft (2004)	$300	Windows XP and higher	Shadish et al. (2009)	91 graphs	r = .999, p < .001	Mean scores from original studies	44 mean scores	r = .959
				Rakap et al. (2016)	1,421 data points from 60 graphs	r = .999, p < .001	Mean scores from original studies	30 mean scores	r = .988
				Moeyaert et al. (2016)	2,805 data points from 28 MBD graphs	Coder consistency over 96% with three other programs, ρc range = .708–1.00, p < .0001	Original raw data from authors	Four MBD graphs	ρc = .982
GraphClick	Arizona-Software (2008)	Free	Mac-OS X	Boyle et al. (2013)	2,223 data points from articles of JABA (between 2006-2010)	r = .999, p < .0001	Hypothetical data	570 data points from 15 hypothetic graphs	r = .999, p < .0001
				Rakap et al. (2016)	1,421 data points from 60 graphs	r = .999, p < .001	Mean scores from original studies	30 mean scores	r = .995
				Flower et al. (2016)	1,438 data points from 17 articles with 45 graphs,	r = .998, p < .0001	Hypothetical data	570 data points from 15 hypothetic graphs (Similar to Boyle et al.)	r = .998, p < .0001
Digitizelt	Bormann (2012)	$49	Windows XP-Windows 10, Mac-OS X, Linux, Unix	Rakap et al. (2016)	1,421 data points from 60 graphs	r = .999, p < .001	Mean scores from original studies	30 mean scores	r = .990
DataThief	Tummers (2006)	$25	Mac-OS X, Windows XP and higher	Flower et al. (2016)	1,438 data points from 17 articles with 45 graphs,	r = .994, p < .0001	Hypothetical data	570 data points from 15 hypothetic graphs (Similar to Boyle et al.)	r = .998, p < .0001
				Moeyaert et al. (2016)	2,805 data points from 28 MBD graphs	Coder consistency over 94% with three other programs, ρc range = .708–1.00, p < .0001	Original raw data from authors	Four MBD graphs	ρc = .982
WebPlotDigitizer	Rohatgi (2015)	Free	Web-based	Moeyaert et al. (2016)	2,805 data points from 28 MBD graphs	Coder consistency over 94% with three other programs, ρc range = .708–1.00, p < .0001	Original raw data from authors	Four MBD graphs	ρc = .982
				Drevon et al. (2017)	3,596 data points from 18 studies with 168 data series	r = .999, p < .001	Tau-U values from original studies	139 Tau-U values	r = .989, p < .001
XYit	Geomatix (2007)	$162	Windows 95-2003	Moeyaert et al. (2016)	2,805 data points from 28 MBD graphs	Coder consistency over 95% with three other programs, ρc range = .708–1.00, p < .0001	Original raw data from authors	Four MBD graphs	ρc = .982

Among these programs, GraphClick (Arizona-Software, 2008) and Webplotdigitizer (Rohatgi, 2015) are available for free access. However, GraphClick only runs on macOS, and its current versions (e.g., macOS Catalina, Big Sur) are not yet available. As Webplotdigitzer is web-based, anyone using Chrome, Safari, or any other browser may access it. The other four programs are paid programs. Also, a program is not always compatible with every operating system. For instance, the most expensive program UnGraph (Biosoft, 2004), is compatible only with Windows. Likewise, XYit (Geomatix, 2007), ranked second in terms of cost, is compatible only with Windows. Although Digitizelt (Bormann, 2012) and DataThief (Tummers, 2006) are compatible with macOS and Windows, their current versions for macOS Catalina or Big Sur are not available. The conducted studies show that the validity and reliability correlation coefficients of the abovementioned programs are rather high and similar (see Table 1).

Other than these programs, another raw data extraction program, which has been used in more than 60 studies in literature according to the Google Scholar citation list, is PlotDigitizer. The program was developed for the first time in 2001 and has undergone numerous revisions so far. The last update of the program was made in late 2020 (the latest version PlotDigitizer 2.6.9; Huwaldt & Steinhorst, 2020). In addition to the many articles in the Google Scholar citation index, many studies that analyze single-case graphs have used this program, and there is no reference to the producers in these studies (e.g., Manolov et al., 2019; Manolov & Rochat, 2015; Odom et al., 2018; Rochat et al., 2018; Zimmerman et al., 2018).

The PlotDigitizer is a Java-supported program that allows extracting raw data from X–Y type scatter or line plots. PlotDigitizer recognizes GIF, JPEG, or PNG images and works with both linear and logarithmic axis scales. It has similar features with other software programs except for some minor details. It has many useful features. For instance, it offers options such as unlimited undo, extracting multiple data series from a calibrated graphic, recalibrating the axis Y without recalibrating the axis X, adding new data to already digitized data, or deleting existing data (for detailed information, visit http://plotdigitizer.sourceforge.net/). PlotDigitizer software program is compatible with macOS, Windows, and Linux operating systems. It also runs on the current macOS Catalina and nowadays Big Sur (not yet available on other software programs).

Although the PlotDigitizer is used extensively in the literature for single-case data digitization, meets the current computer system requirements, is an alternative to other paid and outdated programs, there is no validity study yet, and there is one reliability study (Kadic et al., 2016) for graphs in only the medical field. Kadic et al. (2016) compared the PlotDigitizer with manual extraction on the data extraction of graph models such as column graphs, bar graphs, histograms, and box-and-whiskers graphs widely used in the medical literature. Researchers found that the PlotDigitizer software could digitize faster and enable higher interrater reliability than manual extraction. However, the researchers did not examine the validity study of the PlotDigitizer. Besides, the researchers did not analyze the reliability of the number of correct data-point digitization. Kadic et al. also built their study on comparing manual extraction and extracting with the PlotDigitizer. The researchers did not examine the reliable extraction ability of the PlotDigitizer in different operating systems.

Based on the literature, we have three motivations to conduct this study. First, the PlotDigitizer has some advantages (e.g., compatible with macOS Catalina, Big Sur) compared to other software programs. Second, although single-case researchers commonly use this program to extract data from single-case graphs, there is not yet a validity study, and there is one reliability study performed by Kadic et al. (2016). Third, Kadic et al.’s study has some limitations (e.g., no validity analysis and limited reliability examination, i.e., for only medical field graphs, not for operating systems and the number of correctly digitized data points). Therefore, we realized that the validity and reliability of the PlotDigitizer for single-case graphs need to be rigorously examined.

The Aim of the Study and Research Questions

We aimed to examine the validity and reliability of the PlotDigitizer software program installed on different computers for digitizing single-case graphs widely used in behavior science. Within this scope, we sought to answers the following questions:

• Research Question 1: Does the PlotDigitizer generate reliable results in terms of the number of data points and data values in the digitization of single-case graphs?

• Research Question 2: Does the PlotDigitizer validly digitize data of single-case graphs?

• Research Question 3: Is the use of the PlotDigitizer valid and reliable on different operating systems?

Method

Data Sample

Data for the reliability analysis

When determining the data sample for conducting the present study, we set specific criteria based on the review studies conducted by Shadish and Sullivan (2011) and Smith (2012) to identify the characteristics of the single-case designs used in the articles. First, we identified three journals that were scanned in both review studies and had the highest SCEDs study publication frequency: Journal of Applied Behavior Analysis (JABA), Journal of Autism and Developmental Disabilities (JADDs), and Focus on Autism and Other Developmental Disabilities (FAODDs). Then, we selected the single-case design, which was used the most as per the results of both reviews. This experimental design is multiple baseline (MB) design that covers 54.3% of all SCEDs, according to Shadish and Sullivan (2011) and 69% according to Smith (2012). As another criterion aimed to obtain all MB graphs from the studies published between January 2019 and December 2019. We excluded MB graphs that included other designs (e.g., multielement design, reversal) from the study’s scope to eliminate possible confusion.

According to the proposed sample identification criteria, we obtained 131 data series from 103 graphs from 12 articles in JABA. Furthermore, we achieved 62 data series from 41 graphs from nine articles in JADDs and 49 data series from 42 graphs from eight articles in FAODDs. In total, we obtained 242 data series from 186 graphs in 29 articles from three journals (see Table 2). The first author, who is also the primary coder, took a screenshot of each article’s graphs. Then, he placed the screenshot graphs and the article that included the graphs in question in a file and named the file with the first author’s name and the publication year (e.g., Xyz2019). The first author coded the screenshot graphs with numbers and added small warning notes (e.g., 1-only black, 8-incl post-train) to names of some screenshots to avoid possible confusion among the coders. The created sample file was electronically shared among the coders.

Table 2.

Data sample distribution according to the selected journals

	Number of Articles	Number of MB Graphs	Number of Data Series
JABA	n = 12	n = 103	n = 131
JADDs	n = 9	n = 41	n = 62
FAODDs	n = 8	n = 42	n = 49
Total	n = 29	n = 186	n = 242

Data for the validity analysis

Original raw data of graphs in articles are needed to examine the validity of any data extraction software program. As raw data were not presented in the published studies that we have included in our sample, 15 hypothetical graphs were generated to perform the validity study on the PlotDigitizer by adopting the method of Boyle et al. (2013) and Flower et al. (2016). In their studies, hypothetical graphs with 10 (five graphs), 20 (four), 40 (three), 80 (two), and 160 (one) data points were generated. These 15 hypothetical graphs provided 570 data points for extraction and comparison. Unlike these two studies, in the present study, two data series were presented in five of the hypothetical graphs as some of the actual studies may have cases wherein more than one data series can be presented in a graph. Therefore, 20 data series were generated in a total of 15 graphs.

Consistent with the method used by Boyle et al. and Flower et al., the following hypothetical data were generated: (1) three 10-data-point graphs with single data series, and two 10-data-point graphs with dual data series; (2) three 20-data-point graphs with single data series and one 20-data-point graph with dual data series; (3) two 40-data-point graphs with single data series and one 40-data-point graph with dual data series; (4) graphs with one 80-data-point single data series and one 80-data-point dual data series; and (5) graph with one 160-data-point single data series. Twenty data series obtained from 15 hypothetical graphs comprised a total of 730 data points. These hypothetical data points were created via Microsoft Excel by a researcher experienced in drawing single-case graphs, not one of this study’s authors. First, the researcher presented the graphs he created to the authors and then provided the raw data following the digitization of the graphical data upon the coders’ request.

Another method we followed in the validity study of PlotDigitizer is similar to the method adopted by Drevon et al. (2017) in their study conducted for the validity of the WebPlotdigitizer online software program. Drevon et al. compared the Tau-U values they obtained using the graphical data they digitized with the Tau-U effect sizes obtained from the articles to analyze the program’s validity. In this study, we used a broader effect-size scale and included all studies that analyzed the effect size using the methods Tau-U (Parker et al., 2011), NAP (nonoverlap of all pairs; Parker & Vannest, 2009), IRD (improvement rate difference; Parker et al., 2009), or PND (percentage nonoverlapping data; Scruggs et al., 1987) to our data sampling. We choose these effect-size methods as they are the calculations that both coders know in common. Only 8 out of 29 articles reported the effect size. In six of these studies, the effect-size calculation was performed according to at least one of the effect-size methods identified. We obtained a total of 23 effect-size values, 12 PND values, seven Tau-U values, and four NAP values from six studies.

Coders

Both authors of this study participated in the digitization of all graphs. The first author previously digitized for various studies more than approximately 1,800 single-case graphs using software programs like UnGraph, GraphClick, or PlotDigitizer (e.g., Aydin, under review; Aydin & Diken, 2020; Aydin & Tekin-Iftar, 2020). Due to these extensive experiences, the first author played the role of a primary coder. The secondary coder previously digitized many single-case graphs using the PlotDigitizer. Even so, a small instruction was presented by the primary coder to the second coder via presentation, modeling, rehearsal, and performance feedback on topics such as what data to digitize, how to name the digitized data files, zooming, precision in defining axes to the program to avoid possible confusion before coding. In addition, the primary coder created the PlotDigitizer warning list, provided in Table 3, based on the problems he previously encountered and presented this list to the secondary coder subsequent to the training.

Table 3.

PlotDigitizer use a warning list

Warnings

1. Carefully identify the axes, in particular the Y-axis.

2. Place the data sign right in the exact center of gravity of the shape with the mouse.

3. Mark the data points following the data path without deviating.

4. In complex data, mark subsequent to sufficient zooming in.

5. To ensure that marked all data in the graph, see the marked version of the graph as a whole by zooming out as needed.

6. If any meaningless values instead of zero values (e.g., -1.42109e-14) before saving the data digitization, perform the digitization again.

Apparatus and Data Extraction

Two authors of the study independently digitized all MB graphs (only baseline and intervention data) obtained from 29 studies and 20 data series from 15 hypothetically created graphs, based on Y-axis values, using PlotDigitizer version 2.6.8 (Huwaldt & Steinhorst,2015). The authors did not interact with each other in the data digitization process except for technical issues. The first author of the study digitized all graphs on a MacBook Pro laptop with a 13-in monitor, 3.1 GHz Intel Core i5 processor, and an 8 GB RAM, with macOS Catalina 10.15.2 as the operating system. The secondary author digitized all graphs on a Samsung desktop computer with a 27-in monitor, 3.5 GHz AMD FX-6300 processor, an 8 GB RAM with Windows 7 Ultimate as the operating system, and a MacBook Pro laptop with a 13.3-in monitor, 2.8 GHz Intel Core i7 processor, a 4 GB RAM with macOS X Lion 10.7.5 as the operating system.

PlotDigitizer saves the data it digitizes with csv extension. Both coders combined the csv files in the Microsoft Excel program to prepare them for the validity and reliability analysis. Both coders calculated the effect size based on the data they digitized to compare them with the original effect sizes presented in the articles for the validity analysis. For Tau-U and NAP, effect-size values were obtained using the website http://www.singlecaseresearch.org. PND was manually calculated considering the digitized values. Tau-U values were calculated as described in the articles (e.g., Tau-U with baseline correction, weighted Tau-U, or nonoverlap Tau-U).

Data Analysis

In this study, we performed validity and reliability analyses using Pearson correlation analysis except for the reliability of the number of digitized data points. We calculated the reliability of the number of data points using the following formula:

$$\frac{\text{Number of Common Correctly Digitized Data Points}}{\text{Number of Data Points Need To}\mathrm{Be}\text{Correctly Digitized}}\times 100.$$

We also determined the average agreement percentage obtained according to this formula as test proportion and conducted the binomial test to examine the reliability of the number of digitized data points. We performed other analyses following an agreement reached between the coders on the number of digitized data points.

The data points digitized by the primary coder on the computer with the macOS were compared with the data points digitized by the secondary coder on both macOS and Windows operating systems separately in the reliability analyses. Also, the reliability analysis of the secondary coder’s digitization of data on macOS and Windows operating systems was examined using correlation analysis.

In this study, we considered previously adopted approaches to perform the validity analysis. In the validity analysis of previous studies, a gold standard was created either by considering (1) the mean values (e.g., Rakap et al., 2016; Shadish et al., 2009); (2) effect sizes (e.g., Drevon et al., 2017) derived from published studies; (3) original raw data (e.g., Moeyaert et al., 2016) taken from authors, or (4) original raw data from hypothetical graphs (e.g., Boyle et al., 2013; Flower et al., 2016). In our opinion, as multiple data points are used to obtain a single value, such as mean or effect size, it may be inconvenient to accept those values as gold standards. On the other hand, the rates of getting original raw data from article authors are low (see Moeyaert et al., 2016). Therefore, in the present study, both the singular effect-size values obtained using multiple values from published studies (thereby reducing possible bias) and each hypothetical data point (thereby increasing the reliability) are defined as two gold standards. We performed reliability analysis by comparing the digitized values and effect-size values obtained by the primary coder with those of the secondary coder. The validity analysis of the primary coder’s values and the values considered as the gold standard was performed using correlation analysis.

Results

Reliability of the Number of Digitized Data Points

The primary coder digitized 6,083 data points from the graphs in 29 studies using the PlotDigitizer. The secondary coder digitized 6,106 data on the Windows operating system and 6,127 data on the macOS. The primary coder and secondary coder discussed the graphical images to make the appropriate decisions regarding the data points they could not agree on; in other words, they did not digitize or they overdigitized. Based on this discussion, the primary coder obtained 34 missing data points from eight graphs and digitized an extra data point in one graph. The second coder obtained 13 missing data points from eight graphs on the computer using Windows operating system and digitized three extra data points in three graphs. The second coder digitized 17 extra data points in nine graphs on the macOS operating system and six missing data from five graphs. The two coders then reached a consensus on the incompatibilities in the number of data points digitized in graphs and stated that there were 6,116 data points in all graphs. Both coders redigitized the missing data points and removed surplus points from the data.

We calculated the reliability of the number of data points digitized from published studies by the primary and secondary coders as 99.1% for Windows (range among the graphs: 85%–100%) and 99.05% for macOS (range among the graphs: 83.5%–100%). In the reliability of the number of hypothetical data points, the primary coder digitized all 730 data points, whereas the secondary coder digitized 729 on Windows and 728 on macOS, and we calculated the reliabilities as 99.8% and 99.7%, respectively. The intracoder reliability for the number of data points digitized by the secondary coder was 99.3% (range among the graphs: 95%–100%) and 99.5%, respectively, for published study graphs and hypothetical data.

After the percent agreement was calculated, we assigned the test proportion value to be .99. According to the binomial test results (see Table 4), the number of correct data-point digitization of the primary coder was significant for the .99 level (p < .0001). Likewise, the number of correct digitization of the secondary coder with both macOS and Windows operating systems was significant for the .99 level (p < .0001).

Table 4.

Binomial test for the number of correct digitization of the coders

Coders	Category	N	Percentage (Approximately)	Test Proportion	p
Primary Coder (MacOS)	Correctly Digitized Data Points	6,812	.99	.99	.000
	False/Missing Digitized Data Points	35	.01
Secondary Coder for Windows	Correctly Digitized Data Points	6,832	.99	.99	.000
	False/Missing Digitized Data Points	17	.01
Secondary Coder for MacOS	Correctly Digitized Data Points	6,838	.99	.99	.000
	False/Missing Digitized Data Points	25	.01

Reliability Coefficients

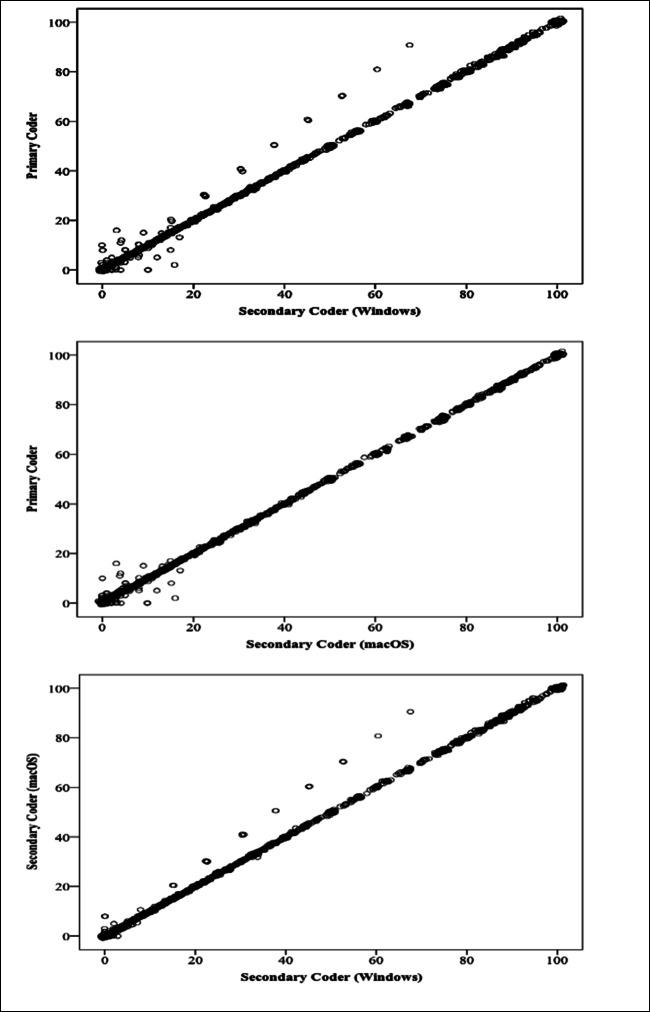
The correlation between the values digitized by the primary coder on macOS and the values digitized by the secondary coder both on Windows and macOS was analyzed using the PlotDigitizer through the calculation of inter- and intracoder reliability coefficients. In the digitization of the graphs obtained from published studies, we found the reliability coefficient of the values digitized by the primary and secondary coder on Windows and macOS to be r = .999, p < .0001 (see Fig. 1). The data deviation resulting from the secondary coder’s inaccurate axis definition in the digitization of one graph is seen in Fig. 1 among the values digitized on Windows. As the secondary coder did not make this error during the digitization process on macOS, the data distribution linearly proceeds with that of the primary coder. The intracoder correlation coefficient of the secondary coder’s digitized values on Windows and macOS was r = .999, p < .0001 (see Fig. 1).

Fig. 1.

Inter-coder and intra-coder scatterplot graphs according to the digitization of article graphs

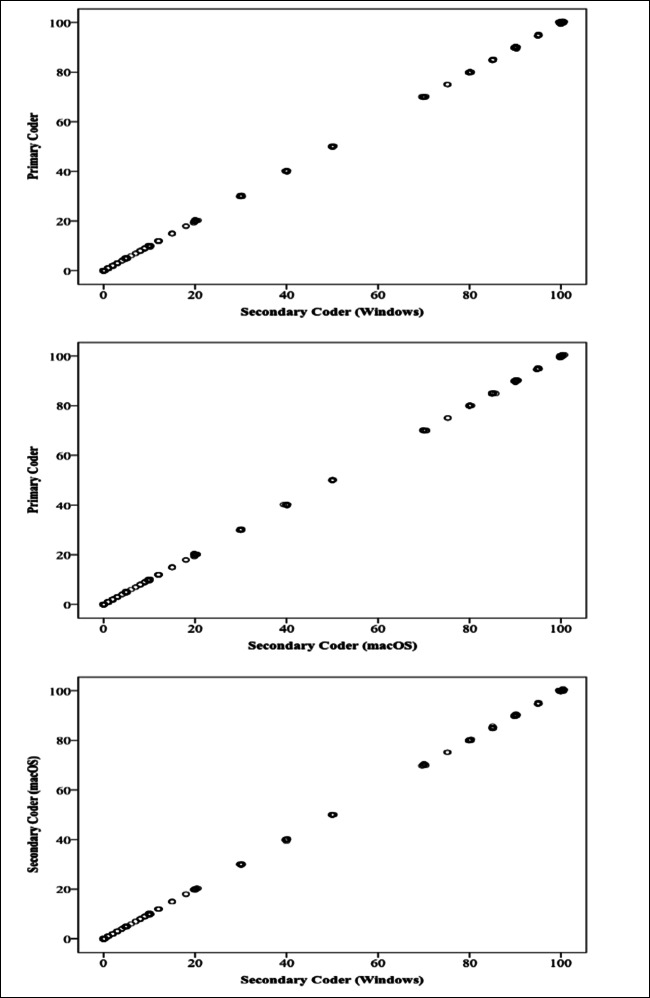
We also analyzed the reliability of the data sample we determined to perform the validity analysis. In the digitization of hypothetical graphs, the reliability coefficient for the values digitized by the primary and secondary coders was r = .999, p < .0001 for both Windows and macOS (see Fig. 2). The intracoder reliability coefficient of the hypothetical values digitized by the secondary coder on Windows and macOS was r = .999, p < .0001 (see Fig. 2).

Fig. 2.

Inter-coder and intra-coder scatterplot graphs according to the digitization of hypothetical data

We obtained two sets of 23 effect sizes from the graphs whose effect-size values were presented in the articles to perform validity analysis. One was calculated with the digitized values converted to the nearest integer, and the other with nonconverted the original digitized (decimal) values. The intercoder reliability coefficient of the primary and secondary coders in the effect-size values calculated with decimal digitized values was r = .81, p < .0001 for Windows and r = .949, p < .0001 for macOS. The intercoder reliability coefficient of the primary and secondary coders in the effect-size values calculated with the values converted to the nearest integer was r = .988, p < .0001 for Windows and r = .947, p < .0001 for macOS. The intracoder reliability coefficient between the effect sizes calculated with decimal values digitized by the secondary coder on Windows and macOS operating systems was r = .834, p < .0001, whereas the intracoder reliability coefficient between the effect-size values calculated with the values converted to the nearest integer was found to be r = .947, p < .0001.

Validity Coefficients

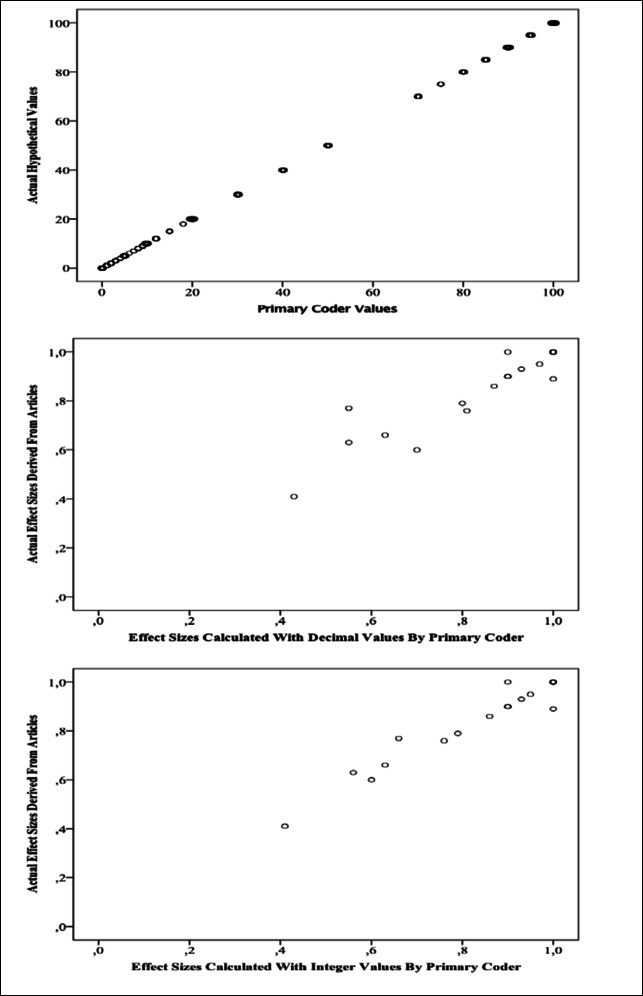
We adopted the effect sizes presented in the studies and the hypothetical data points generated by an independent researcher as two different gold standards and calculated the validity coefficients by comparing these values with the primary coder’s values. The validity coefficient between the effect sizes calculated with decimal values digitized by the primary coder and the 23 effect-size values presented in the studies was r = .929, p < .0001 (see Fig. 3). The validity coefficient between the actual effect sizes and the effect sizes calculated with the values converted to the nearest integer of the primary coder’s data digitized was r = .971, p < .0001 (see Fig. 3). Two of the effect sizes presented in the studies were incorrectly reported (according to authors’ calculations; one value in PND, other value in Tau-U), and when we corrected these values, the validity coefficient of the reported effect sizes and the effect sizes calculated with integer values increased to r = .989. We calculated the validity coefficient between the hypothetical 730 data points and those digitized by the primary coder to be r = .999, p < .0001 (see Fig. 3).

Fig. 3.

Scatterplot graphs showing the correlation between the primary coder’s values and the actual vsalues

Discussion

We analyzed the validity and reliability of digitizing single-case graphs using the PlotDigitizer on different operating systems in this study. The findings resulted in near-perfect valid and reliable data extraction using this software program. These results were similar to the validity and reliability results of other data extraction programs such as UnGraph (Rakap et al., 2016; Shadish et al., 2009), GraphClick (Boyle et al., 2013; Flower et al., 2016; Rakap et al., 2016), Webplotdigitizer (Drevon et al., 2017; Moeyaert et al., 2016), and Digitizelt (Rakap et al., 2016). These findings are in line with Kadic et al.’s (2016) study, which has findings that the PlotDigitizer program can be used reliably to digitize graph models other than single case.

The reliability of the number of data points digitized with PlotDigitizer was fairly high. These results are similar to the researchers’ results (Boyle et al., 2013; Drevon et al.,2017; Rakap et al., 2016; Shadish et al., 2009), who analyzed the reliability of the number of data points that were digitized with other programs. Based on the error analysis performed, we determined that the incompatibility cases in the number of data points were related to (1) the under- or overdigitization of adjacent data due to the use of a small screen (e.g., 13-in); (2) inadvertent repetitive digitization of a data; (3) digitization of maintenance data in graphs without a phase change line; (4) inability to follow the data path; and (5) missing digitization when two data overlaps in graphs with two different data paths. We obtained the lowest reliability values in terms of the number of digitized data points (i.e., 83.5% and 85%) from a few graphs where the data points overlap excessively (e.g., Radley et al., 2019; Wichnick-Gillis et al., 2019). The use of the small screens in digitization triggered this case even more.

The correlation coefficients of the values digitized using the PlotDigitizer on different operating systems were quite high for inter- and intracoder values. These findings suggest that the PlotDigitizer can be used validly and reliably on computers with different features and different operating systems. Although the reliability of data extraction was nearly perfect, we can still offer some recommendations for more precise measurements similar to what other researchers (e.g., Boyle et al., 2013; Rakap et al., 2016) reported. First, the Y-axis (dependent variable values) must be well-defined. However, we encountered thick axis lines in published studies, which reduced the accuracy of defining the Y-axis. Second, the exact center of gravity of the data points must be marked. However, we encountered graphs where extremely large data points were illustrated. We noticed that marking must be more precise in such cases. Third, in the case of many data points and multiple data series, following the data path requires utmost attention. In the studies, when different data series are presented in a graph, each data path is illustrated with different lines such as dashed, dotted, or straight lines. The digitizer should carefully follow the relevant data path throughout the graph.

In general, we obtained the digitized values as decimal values. Calculating the effect sizes considering decimal values may lead to incorrect results. Therefore, decimal values can be converted to the nearest integer in applications such as Excel. However, it would be useful to look at the graphs again when converting all digitized values to the nearest integer to ensure accurate measurements in effect-size calculations. Otherwise, in particular in the case of overlapping data in two phases, errors may occur even if the values obtained in decimals are automatically converted to integers. For instance, although the closest integer value of a value digitized as 9.48 in phase A is 9, if this value is digitized as 9.62 in phase B, the nearest integer value will be 10. In such a case, overlapping-based effect-size calculations, commonly used in single-case studies, may result in errors.

We encountered many graph samples in this study. We believe that for the researchers trying to extract raw data from such graphs, the quality of the graphs can be increased by the following: (1) drawing thin axis lines; (2) a clear data path; (3) presenting the data points in typical sizes (e.g., 6 pt); and (4) distinctively presenting the adjacent points in the graphs wherein a large number of data points are presented. Apart from these, expecting authors to present raw data in their articles would be unrealistic due to the disruption of a reader-friendly flow and the page/word limitations of journals. Instead, we recommend researchers present the original raw data they used in graphs in online platforms accessible to all (e.g., https://osf.io/) according to open science principles. Accessing the original data would be a unique source for the researchers to reanalyze the data in question. Moreover, this sharing would increase the scientific credibility and transparency of studies (Cook et al., 2018).

Strengths of Current Study

Our study expands the literature in terms of five strengths. First, the current study is superior in that it uses much more data (6,846) than the number of data used in other studies (approximately between 1,000 and 3,500) to analyze reliability and validity. Second, our study is the first study to examine the PlotDigitizer’s validity and analyze its reliability on single-case graphs. Third, the current study is one of the first studies to examine the validity and reliability of a data extraction software program in different operating systems. Fourth, our study is superior to other studies by performing the validity analysis with two gold standards. Finally, the current study is one of the rare studies examining the reliability of the number of correctly digitized data points.

Limitations and Recommendations

We realized four limitations in our study. First, we did not compare the digitization performed using the PlotDigitizer with the digitization performed using other programs whose validity and reliability have already been proved, and we did not test the software in terms of practicality. Future studies can analyze which extraction would be more practical with the programs whose validity and reliability have already been proved. Second, only two coders performed the extraction in this study. Involving more coders could have increased credibility for validity and reliability. Third, although it is an advantage that access to the PlotDigitizer is free and it is compatible with many current or outdated operating systems, in rare cases, it may generate meaninglessly (e.g., -1.34901e-13) results in the digitization of zero values. Elimination of this error by developers via an update (maybe possibly fixed in version 2.6.9) will make the software error-free. Last, in our study, we only considered single-case graphs. PlotDigitizer can be used for digitizing different graph models (e.g., histogram, bar, box-and-whiskers). Future research can examine the PlotDigitizer in terms of the usefulness, and validity and reliability in digitizing different graph types.

Conclusion

Technology is dramatically developing and offering numerous software for the benefit of humanity. For such software to be deemed suitable for presenting scientific data, it is crucial to conduct studies that evidence its validity and reliability. In this study, the validity and reliability of the digitization of X–Y type single-case graphs were analyzed with the PlotDigitizer software program. Results show that extracting digitized values from graphs with the PlotDigitizer on different operating systems offers valid and reliable results at high coefficients. Although the program’s use is easy, providing a brief training and presenting a list of warnings to avoid user errors may lead to useful results. Also, the direct use of digitized data is not recommended due to possible human-induced errors. Digitized data must be verified by looking at the graphs again, and decimal values must be converted to the nearest integer and used in further analysis. Researchers who will calculate the effect size by extracting raw data from the graphs in articles can reliably use the PlotDigitizer to digitize SCEDs graphs and confidently perform studies such as meta-analysis provided that they follow the warnings above.

Declarations

Ethical Approval

Only published data sets were used for the analyses.

Conflict of interest

There is no conflict of interest for the article.

Data availability

All original documents can be provided by the corresponding author.

Funding

There is no funding for this study.