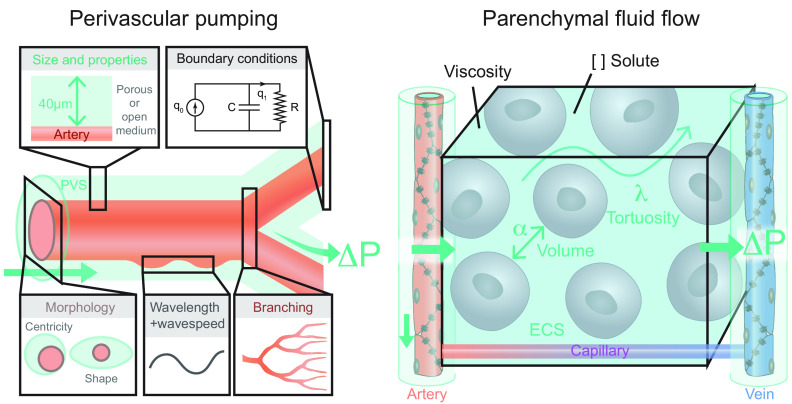
FIGURE 22.

Overview of existing models evaluating intra-axial fluid transport. The two main types of models are perivascular pumping (left) and parenchymal fluid flow (right). Perivascular pumping models consist of an artery with a surrounding perivascular space (PVS). Most such models implement a concentric anulus in which the artery lies central to the larger PVS, but modifying the centricity and the shape of the PVS cross-section to better represent in vivo measurements greatly reduces the calculated hydraulic resistance (409). The size and porosity (or lack thereof) of the PVS also affect the hydraulic conductivity (21, 409) The velocity of the arterial pulsation (wave speed) divided by the frequency of the pulsation (heart rate) indicates the wavelength. Models have used wide ranges of wavelengths due to the difference in resting heart rates between mice and humans, and due to inconsistent use of pulse wave velocity measurements collected from different blood vessels and species (278). Including outflowing boundary conditions such as intracranial compliance (C) and cranial cerebral spinal fluid outflow resistance (R) modifies the volume flow rate through the system (554). Few studies have evaluated how vascular branching and bifurcations affect wave speed transmission and arterial rigid motions (411, 555). The majority of perivascular pumping models have found that a static pressure gradient (ΔP) across the PVS is required for arterial pulsations to drive net flow at a rate comparable to those measured in vivo (21, 282, 555, 556). Parenchymal fluid flow models primarily consist of a segment of brain tissue interposed between an artery and a vein. The majority of such models to date have not included the interposed capillary network, which could but present an interesting extension. The extracellular space (ECS) geometry can be idealized or reconstructed from serial electron microscopic images. The volume and tortuosity of the ECS is approximated using the alpha (α) and lambda (λ) terms measured from real time iontophoresis experiments. The viscosity and concentration of solutes in the extracellular fluid can also be defined in these models. Static pressure gradients from the arterial side to the venous side have been tested as possible drivers of parenchymal fluid flow.