Fast computation of latent correlations

Abstract

Latent Gaussian copula models provide a powerful means to perform multi-view data integration since these models can seamlessly express dependencies between mixed variable types (binary, continuous, zero-inflated) via latent Gaussian correlations. The estimation of these latent correlations, however, comes at considerable computational cost, having prevented the routine use of these models on high-dimensional data. Here, we propose a new computational approach for estimating latent correlations via a hybrid multilinear interpolation and optimization scheme. Our approach speeds up the current state of the art computation by several orders of magnitude, thus allowing fast computation of latent Gaussian copula models even when the number of variables p is large. We provide theoretical guarantees for the approximation error of our numerical scheme and support its excellent performance on simulated and real-world data. We illustrate the practical advantages of our method on high-dimensional sparse quantitative and relative abundance microbiome data as well as multi-view data from The Cancer Genome Atlas Project. Our method is implemented in the R package mixedCCA, available at https://github.com/irinagain/mixedCCA.

1. Introduction

Multi-view data, i.e, data collected on the same subjects from different sources or views, are becoming increasingly common in the biomedical world thanks to advances in biological high-throughput technologies. Large-scale data collections, such as The Cancer Genome Atlas project (Cancer Genome Atlas Research Network et al., 2013), make concurrent gene expression, methylation, mutation, and other data views with a mixed type of measurements (e.g., continuous, binary) readily available for multi-view data analysis. Moreover, recent sequencing-based technologies provide an abundance of high-dimensional biological data with excess zeros, ranging from Chip-Seq to targeted amplicon and single-cell sequencing data. Many statistical analysis routines start with estimating covariances and correlations from the different variables. Standard maximum likelihood estimation of the Pearson sample covariance matrix is, however, not well suited for these data since it cannot handle the excess zeros in the data, and its underlying normality assumption is often violated by the highly skewed empirical data distributions.

Latent Gaussian copulas offer an elegant alternative for the analysis of multi-view data as they model associations between mixed variable types on the common latent Gaussian level rather than on the mixed observed data level. Liu et al. (2009) capture possible skewness in continuous measurements via Gaussian copula models. Fan et al. (2017) capture binary measurements via an extra dichotomization step of Gaussian copulas, thus enabling joint modeling of continuous and binary variables. Extensions to ordinal variables have also been considered (Quan et al., 2018; Feng and Ning, 2019). Yoon et al. (2020, 2019) capture variables with excess zeros via an extra truncation step in Gaussian copulas, thus enabling joint modeling of continuous, binary, and truncated (excess zeros) data types. These models are very flexible and capture all dependencies via the common latent correlation matrix, which is estimated based on a robust rank-based measure of association (Kendall’s Τ). By replacing Pearson sample correlation estimators with a rank-based correlation matrix estimator, latent Gaussian copula models have been shown to improve graphical model estimation (Liu et al., 2009; Fan et al., 2017; Feng and Ning, 2019; Yoon et al., 2019), canonical correlation analysis (Yoon et al., 2020), and discriminant analysis (Han et al., 2013).

Despite the clear advantages offered by the latent Gaussian copula models, their widespread use on high-dimensional biological data has been hindered by the considerable computational cost associated with the estimation of the latent correlation matrix Σ. Let σ_jk be the latent correlation between variables j and k, and ${\widehat{\tau }}_{jk}$ be the corresponding sample Kendall’s Τ. The two quantities are connected via a strictly increasing bridge function F such that $\mathbb{E}({\widehat{\tau }}_{jk})=F({\sigma }_{jk})$. This moment equation motivates the estimator ${\widehat{\sigma }}_{jk}=F^{-1}({\widehat{\tau }}_{jk})$. While the explicit form of F has been derived for multiple variable types (Fan et al., 2017; Quan et al., 2018; Feng and Ning, 2019; Yoon et al., 2020), its inverse F⁻¹ is not available in closed form. As a result, the estimation requires solving a uniroot non-linear equation $F(x)={\widehat{\tau }}_{jk}$ for every element of Σ. When the number of variables p is very large, this becomes computationally expensive. The computational cost also depends on the type of variables (as it influences the form of F), and is especially problematic for truncated variable types, i.e., for data with excess zeros such as single-cell and microbiome data. For instance, single-threaded computation of latent correlations on a subset of the American Gut amplicon data (McDonald et al., 2018) with p = 481 species can take almost an hour on a standard computer (Yoon et al., 2019). This makes repeated computations over sub-sampled or bootstrapped data or data with thousands of variables computationally demanding.

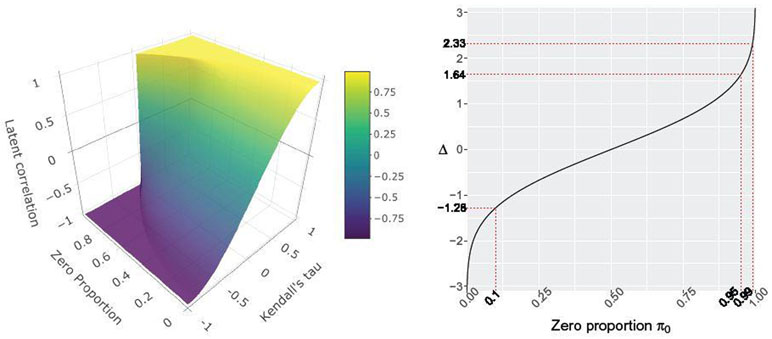
Here, we overcome this challenge via a novel fast computation approach. Our idea is based on the observation that, even though the exact analytic form of the inverse bridge function F⁻¹ is unknown, it is amenable to accurate multilinear interpolation of pre-computed function values over a well-chosen fixed grid of points. This pre-computation only needs to be done once for each pair of variable types (continuous/binary/truncated) and is then readily available for any new dataset. Our interpolation scheme leads to a dramatic reduction in computational cost (e.g., latent correlation on the American Gut microbiome data now only takes five minutes) while simultaneously controlling the approximation error required for statistical estimation. To provide a visual illustration of the interpolation challenge, Figure 1 shows the surface of the inverse bridge function for the continuous/truncated variables pair, F⁻¹(τ, π₀), which depends on the value of the sample Kendall’s Τ and the observed proportion of zeros π₀. While the function is strictly increasing for each fixed value of π₀, its smoothness decreases significantly when π₀ increases. We present a hybrid interpolation scheme that approximates the smooth part of the surface by multilinear interpolation of pre-computed function values over the fixed grid of points to obtain F⁻¹(τ_i, π_0k), and explicit univariate non-linear optimization for the non-smooth part.

Fig. 1.

(Left) Inverse bridge function 1 F⁻¹(τ, π₀) for the continuous/truncated variables pair. The arguments are Kendall’s Τ (x-axis) and the proportion of zeros π₀ in the truncated variable (y-axis). The function values correspond to latent correlations (z-axis). (Right) The estimated latent cutoff level Δ versus the proportion of zeros π₀ based on the moment equation $\widehat{\Delta }={\Phi }^{-1}({\pi }_0)$.

The rest of the paper is organized as follows. In Section 2, we review the latent Gaussian copula model for mixed data and the existing computational approach for latent correlation estimation. In Section 3, we propose a new fast computation based on interpolation and provide theoretical guidance on the approximation error. In Section 4, we assess the empirical performance both in terms of accuracy and speed on several high-throughput biological datasets. Section 5 concludes with a discussion and future challenges. Our method is available in the R package mixedCCA at https://github.com/irinagain/mixedCCA. A reproducible workflow of the presented numerical results is available at https://github.com/GraceYoon/Fast-latent-correlation.

2. Latent correlation of latent Gaussian copula model

2.1. Latent Gaussian copula model for mixed data

We begin by reviewing the Gaussian copula model, or non-paranormal (NPN) model, of Liu et al. (2009) for possibly skewed continuous data, e.g., gene expression data.

Definition 1 (Continuous model). A random $\mathbf{X}\in {\mathbb{R}}^p$ satisfies the Gaussian copula model if there exist monotonically increasing $f=(f_j{)}_{j=1}^p$ with Z_j = f_j(X_j) satisfying Z ~ N_p (0, Σ), σ_jj = 1; X ~ NPN(0, Σ, f).

For binary data (e.g., mutation data), Fan et al. (2017) propose a generalization of Gaussian copulas via an extra dichotomization step.

Definition 2 (Binary model). A random $\mathbf{X}\in {\mathbb{R}}^p$ satisfies the binary latent Gaussian copula model if there exists W ~ NPN(0, £, f) such that X_j = I(W_j > c_j), where I(·) is the indicator function and c_j are constants.

The binary model has been extended to ordinal variables with more than two levels (Quan et al., 2018; Feng and Ning, 2019). For data with excess zeros, such as microbiome and single-cell data, Yoon et al. (2020) propose an extra truncation step in Gaussian copulas.

Definition 3 (Truncated model). A random $\mathbf{X}\in {\mathbb{R}}^p$ satisfies the truncated latent Gaussian copula model if there exists W ~ NPN(0, Σ, f) such that X_j = I (W_j > c_j)W_j, where I (·) is the indicator function and c_j > 0 are constants.

The mixed latent Gaussian copula model jointly models W = (W₁, W₂, W₃) ~ NPN(0, Σ, f) such that X_1j = W_1j, X_2j = I(W_2j > c_2j) and W_3j = I(W_3j > c_3j)W_3j.

2.2. Bridge function

The latent correlation matrix Σ is the key parameter in Gaussian copula models. Estimation of latent correlations is achieved via the bridge function F such that $\mathbb{E}({\widehat{\tau }}_{jk})=F({\sigma }_{jk})$, where σ_jk is the latent correlation between variables jand k, and ${\widehat{\tau }}_{jk}$ is the corresponding sample Kendall’s Τ. Given observed

$$\begin{gathered} {\mathbf{x}}_j,{\mathbf{x}}_k\in {\mathbb{R}}^n, \\ {\widehat{\tau }}_{jk}=\widehat{\tau }({\mathbf{x}}_j,{\mathbf{x}}_k)=\frac{2}{n(n-1)}\sum _{1\le i<i^{\prime }\le n}\mathrm{sign}(x_{ij}-x_{i^{\prime }j})\mathrm{sign}(x_{ik}-x_{i^{\prime }k}), \end{gathered}$$ (1)

where n is the sample size. Using F, one can construct ${\widehat{\sigma }}_{jk}=F^{-1}({\widehat{\tau }}_{jk})$ with the corresponding estimator Σ being consistent for Σ (Fan et al., 2017; Quan et al., 2018; Yoon et al., 2020). The explicit form of F has been derived for all combinations of continuous(C)/binary(B)/truncated(T) variables (Fan et al., 2017; Yoon et al., 2020). We summarize these results below, and use CC, BC, TC, etc. to denote corresponding combinations.

Theorem 1. Let ${\mathbf{W}}_1\in {\mathbb{R}}^{p_1}$, ${\mathbf{W}}_2\in {\mathbb{R}}^{p_2}$, ${\mathbf{W}}_3\in {\mathbb{R}}^{p_3}$ be such that W = (W₁, W₂, W₃) ~ NPN(0, Σ, f) with p = p₁ + p₂ + p₃. Let $\mathbf{X}=({\mathbf{X}}_1,{\mathbf{X}}_2,{\mathbf{X}}_3)\in {\mathbb{R}}^p$ satisfy X_j = W_j for j = 1,…, p₁, X_j = I(W_j > c_j) for j = p₁ + 1,…, p₁ + p₂ and X_j = I(W_j > c_j)W_j for j = p₁ + p₂ + 1,…, p with Δ_j = f (c_j). The rank-based estimator of Σ based on the observed n realizations of X is the matrix $\widehat{\mathbf{R}}$ with ${\widehat{r}}_{jj}=1$, ${\widehat{r}}_{jk}={\widehat{r}}_{kj}=F^{-1}({\widehat{\tau }}_{jk})$ with block structure

$$\begin{gathered} \widehat{\mathbf{R}}=\left(\begin{array}{ccc}\hfill F_{\text{CC}}^{-1}(\widehat{\tau })\hfill & \hfill F_{\text{CB}}^{-1}(\widehat{\tau })\hfill & \hfill F_{\text{CT}}^{-1}(\widehat{\tau })\hfill \\ \hfill F_{\text{BC}}^{-1}(\widehat{\tau })\hfill & \hfill F_{\text{BB}}^{-1}(\widehat{\tau })\hfill & \hfill F_{\text{BT}}^{-1}(\widehat{\tau })\hfill \\ \hfill F_{\text{TC}}^{-1}(\widehat{\tau })\hfill & \hfill F_{\text{TB}}^{-1}(\widehat{\tau })\hfill & \hfill F_{\text{TT}}^{-1}(\widehat{\tau })\hfill \end{array}\right) \\ {F}_{\text{CC}}(r)=\frac{2}{\pi }{\sin }^{-1}(r) \\ {F}_{\text{BB}}(r;{\Delta }_j,{\Delta }_k)=2\left\{{\Phi }_2({\Delta }_j,{\Delta }_k;r)-\Phi ({\Delta }_j)\Phi ({\Delta }_k)\right\} \\ {F}_{\text{BC}}(r;{\Delta }_j)=4{\Phi }_2({\Delta }_j,0;r∕\sqrt{2})-2\Phi ({\Delta }_j) \\ {F}_{\text{TB}}(r;{\Delta }_j,{\Delta }_k)=2\{1-\Phi ({\Delta }_j)\}\Phi ({\Delta }_k)-2{\Phi }_3\left(-{\Delta }_j,{\Delta }_k,0;{\Sigma }_{3a}(r)\right)-2{\Phi }_3\left(-{\Delta }_j,{\Delta }_k,0;{\Sigma }_{3b}(r)\right) \\ {F}_{\text{TC}}(r;{\Delta }_j)=-2{\Phi }_2(-{\Delta }_j,0;1∕\sqrt{2})+4{\Phi }_3\left(-{\Delta }_j,0,0;{\Sigma }_3(r)\right) \\ {F}_{\text{TT}}(r;{\Delta }_j,{\Delta }_k)=-2{\Phi }_4(-{\Delta }_j,-{\Delta }_k,0,0;{\Sigma }_{4a}(r))+2{\Phi }_4(-{\Delta }_j,-{\Delta }_k,0,0;{\Sigma }_{4b}(r)), \end{gathered}$$

with

$$\begin{gathered} {\Sigma }_{3a}(r)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill -r\hfill & \hfill 1∕\sqrt{2}\hfill \\ \hfill -r\hfill & \hfill 1\hfill & \hfill -r∕\sqrt{2}\hfill \\ \hfill 1∕\sqrt{2}\hfill & \hfill -r∕\sqrt{2}\hfill & \hfill 1\hfill \end{array}\right),{\Sigma }_{3b}(r)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill -1∕\sqrt{2}\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -r∕\sqrt{2}\hfill \\ \hfill -1∕\sqrt{2}\hfill & \hfill -r∕\sqrt{2}\hfill & \hfill 1\hfill \end{array}\right), \\ {\Sigma }_3(r)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 1∕\sqrt{2}\hfill & \hfill r∕\sqrt{2}\hfill \\ \hfill 1∕\sqrt{2}\hfill & \hfill 1\hfill & \hfill r\hfill \\ \hfill r∕\sqrt{2}\hfill & \hfill r\hfill & \hfill 1\hfill \end{array}\right),{\Sigma }_{4a}(r)=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 1∕\sqrt{2}\hfill & \hfill -r∕\sqrt{2}\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -r∕\sqrt{2}\hfill & \hfill 1∕\sqrt{2}\hfill \\ \hfill 1∕\sqrt{2}\hfill & \hfill -r∕\sqrt{2}\hfill & \hfill 1\hfill & \hfill -r\hfill \\ \hfill -r∕\sqrt{2}\hfill & \hfill 1∕\sqrt{2}\hfill & \hfill -r\hfill & \hfill 1\hfill \end{array}\right) \\ {\Sigma }_{4b}(r)=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill r\hfill & \hfill 1∕\sqrt{2}\hfill & \hfill r∕\sqrt{2}\hfill \\ \hfill r\hfill & \hfill 1\hfill & \hfill r∕\sqrt{2}\hfill & \hfill 1∕\sqrt{2}\hfill \\ \hfill 1∕\sqrt{2}\hfill & \hfill r∕\sqrt{2}\hfill & \hfill 1\hfill & \hfill r\hfill \\ \hfill r∕\sqrt{2}\hfill & \hfill 1∕\sqrt{2}\hfill & \hfill r\hfill & \hfill 1\hfill \end{array}\right). \end{gathered}$$

Here, Φ(·) is the cdf of the standard normal distribution, and Φ_d (·,…,·; Σ) is the cdf of the d-dimensional standard normal distribution with d-dimensional correlation matrix Σ.

2.3. Existing computation

Theorem 1 presents explicit forms of bridge functions for each data type combination. Using the selected bridge function, the computation of the latent correlation between two variables j and k is performed via Algorithm 1. Problem (2) has to be solved for all pairs of variables, leading to O(p²) computations. We refer to this approach as the original (ORG) computation scheme.

Algorithm 1 Original (ORG) method for latent correlation computation

$$\begin{array}{cc}\hfill & \mathrm{Input}:F(r)=F(r,{\Delta }_j,{\Delta }_k)\text{-}\mathsf{bridge}\mathsf{function}\mathsf{based}\mathsf{on}\mathsf{the}\mathsf{type}\mathsf{of}\mathsf{variables}j,k\hfill \\ \hfill & 1.\text{Calculate}{\widehat{\tau }}_{jk}\text{using}(1).\hfill \\ \hfill & 2.\text{For truncated/binary variable}j,\text{set}{\widehat{\Delta }}_j={\Phi }^{-1}({\pi }_{0j})\text{with}\hfill \\ \hfill & {\pi }_{0j}=\sum _{i=1}^{n}I(x_{ij}=0)∕n.\hfill \\ \hfill & 3.\text{Compute}{F}^{-1}({\widehat{\tau }}_{jk})\mathsf{as}\hfill \\ \hfill & {\widehat{r}}_{jk}=\text{arg}\underset{r}{\text{min}}{\left\{F(r)-{\widehat{\tau }}_{jk}\right\}}^2,(2)\hfill \\ \hfill & \text{where}(2)\text{is solved via optimize function in R}.\hfill \end{array}$$

3. Inversion via multilinear interpolation

The inverse bridge function is an analytic function of at most three parameters: (i) Kendall’s Τ, (ii) proportion of zeros in the 1st variable and (possibly) (iii) proportion of zeros in the 2nd variable (see Theorem 1). We propose to pre-calculate the function on a fixed 2d (or 3d) grid and perform multilinear interpolation to estimate its values on a new set of arguments.

3.1. Multilinear interpolation

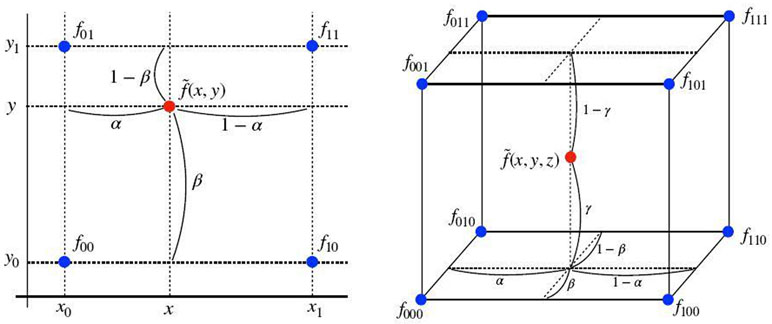
Definition 4 (Bilinear interpolation). Suppose we have 4 neighboring data points f_ij = f (x_i, y_j) at (x_i, y_i) for i, j ∈ {0, 1}. For {(x, y) ∣ x₀ ≤ x ≤ x₁, y₀ ≤ y ≤ y₁}, the biiinear interpolation at (x, y) is

$$\tilde{f}(x,y)=(1-\alpha )(1-\beta )f_{{}_{00}}+(1-\alpha )\beta f_{{}_{01}}+\alpha (1-\beta )f_{{}_{10}}+\alpha \beta f_{{}_{11}},$$ (3)

where α = (x – x₀) / (x₁ – x₀) and β = (y – y₀) / (y₁ – y₀).

Definition 5 (Trilinear interpolation). Suppose we have 8 neighboring data points f_ijk = f (x_i, y_j, z_k) at (x_i, y_j, z_k) for i, j, k ∈ {0, 1}. For {(x, y, z) ∣ x₀ ≤ x ≤ x₁, y₀ ≤ y ≤ y₁, z₀ ≤ z ≤ z₁}, the trilinear interpolation at (x, y, z) is

$$\begin{gathered} \tilde{f}(x,y,z)=(1-\alpha )(1-\beta )(1-\gamma )f_{{}_{000}}+(1-\alpha )(1-\beta )\gamma f_{{}_{001}}+(1-\alpha )\beta (1-\gamma )f_{{}_{010}} \\ +\alpha (1-\beta )(1-\gamma )f_{{}_{100}}+(1-\alpha )\beta \gamma f_{{}_{011}}+\alpha (1-\beta )\gamma f_{{}_{101}}+\alpha \beta (1-\gamma )f_{{}_{110}} \\ +\alpha \beta \gamma f_{{}_{111}}, \end{gathered}$$ (4)

where α = (x – x₀) / (x₁ – x₀), β = (y – y₀) / (y₁ – y₀) and γ = (z – z₀) / (z₁ – z₀).

In short, d-dimensional multilinear interpolation uses a weighted average of 2^d neighbors to approximate the function values at the points within the d-dimensional cube of the neighbors, see Figure 2.

Fig. 2.

Bilinear (Left) and trilinear (Right) interpolation.

3.2. Error bound for multilinear interpolation

Weiser and Zarantonello (1988) provide an error bound for multilinear interpolation.

Theorem 2. For a function $f:{\mathbb{R}}^d\to \mathbb{R}$, assume that the function values are given at 2^d points f(x_1i,…,x_di) for i = 0, 1. Let $\tilde{f}:{\mathbb{R}}^d\to \mathbb{R}$ denote the multilinear interpolation function of f on the d-dimensional cube Ω = {(x₁,…, x_d): x₁₀ < x₁ < x₁₁,…, x_d0 < x_d < x_d1} using the given 2^d neighboring points. Then, for every point x = (x₁,…,x_d)^Τ ∈ Ω

$$\mid f(\mathbf{x})-\tilde{f}(\mathbf{x})\mid \le \frac{d}{8}{h}^2\underset{i=1,\dots ,d}{\text{sup}}\mid \frac{{\partial }^{2}f(\mathbf{x})}{\partial x_i^2}\mid ,$$ (5)

where h = max_j=1,…,d ∣x_j1 – x_j0∣.

Theorem 2 shows that the error bound in our proposed approximation via multilinear interpolation depends on the second derivative of the inverse bridge function. The dimension d = 2 for the BC and TC cases, and d = 3 for the TT, TB, and BB cases. While the inverse bridge functions are differentiable, the explicit forms of the derivatives are difficult to calculate analytically. Nevertheless, we were able to derive explicit bounds for the BC and the TC case, respectively, thus providing theoretical guidance on the aspects of the models that affect interpolation accuracy. The proofs are in the Supplementary Materials.

Theorem 3. Let F⁻¹ (τ, Δ) be the inverse bridge function for the binary/continuous case. Let Δ satisfy ∣ Δ ∣≤ M for some constant M. Then

$$\mid F^{-1}(\tau ,\Delta )-{\tilde{F}}^{-1}(\tau ,\Delta )\mid \le 2h^2\mid F^{-1}(\tau ,\Delta )\mid (2M^2+1)\text{exp}(M^2),$$ (6)

where h is the maximal grid width.

Theorem 3 shows that the approximation error in the BC case strongly depends on the absolute size of Δ. Since we estimate Δ as Φ⁻¹(π₀) (Algorithm 1), and π₀ is the observed proportion of zeros, Theorem 3 implies that the approximation is more accurate when the numbers of zeros and ones are balanced (Δ ≈ 0), and less accurate when they are unbalanced (see left panel in Figure 1 for the correspondence between Δ and π₀). The dependence on the latent correlation r = F⁻¹(τ, Δ) is less strong. Nonetheless, the accuracy decreases as ∣ r ∣ increases.

Theorem 4. Let F⁻¹(τ, Δ) be the inverse bridge function for the truncated/continuous case. Let Δ be such that Δ ≤ M for some positive constant M. Then

$$\mid F^{-1}(\tau ,\Delta )-{\tilde{F}}^{-1}(\tau ,\Delta )\mid \le \frac{4h^2}{{\left\{\Phi (-\sqrt{2}M)\right\}}^2}\max \left(\frac{\mid F^{-1}(\tau ,\Delta )\mid }{\Phi (-\sqrt{2}M)},\sqrt{1-{\left\{F^{-1}(\tau ,\Delta )\right\}}^2}\right),$$ (7)

where h is the maximal grid width.

Theorem 4 shows that the approximation error in the TC case strongly depends on how large is Δ. This is similar to the BC case. However, in the TC case, Δ only needs to be bounded from above. This is because as Δ goes to negative infinity, the truncated data type gets closer to the continuous one as the proportion of zeros π₀ goes to zero (see left panel in Figure 1). On the other hand, as M increases, $\Phi (-\sqrt{2}M)$ goes to 0 making the upper bound in Theorem 4 very large. For example, if M = 1.64 (95% zeros, see Figure 1), then $1∕\Phi (-\sqrt{2}M{)}^3\approx 945099$. The size of the latent correlation has a milder effect on accuracy. Nonetheless, the accuracy decreases as ∣ r ∣=∣ F⁻¹(τ, Δ)∣ increases.

In summary, the approximation accuracy of our approach is affected by the observed proportion of zeros (through the size of M) and by the size of latent correlation (the actual function value at the interpolation point). The interpolation accuracy is poor for binary data when the numbers of zeros and ones are extremely unbalanced, and for truncated data when the proportion of zero values is close to 1.

Remark 1. The estimation consistency of the original method (Algorithm 1) is established under conditions that all correlation values are bounded away from one, and that the values of Δ are bounded (Fan et al., 2017; Yoon et al., 2020). Theorems 3–4 reveal that the same conditions are required for good interpolation approximation, thus emphasizing a close connection between statistical (estimation) and computational (approximation) accuracy.

3.3. Numerical implementation

Algorithm 2 summarizes the multilinear interpolation approach.

Algorithm 2 Multilinear interpolation (ML) method for latent correlation computation

$$\begin{array}{cc}\hfill & \mathrm{Input}:\mathsf{Pre}\text{-computed values}{F}^{-1}({\tau }_l,{\Delta }_m,{\Delta }_q)\mathsf{on}\mathsf{a}\mathsf{fixed}\mathsf{grid}({\tau }_l,{\Delta }_m,{\Delta }_q)\in \mathcal{G}\hfill \\ \hfill & \mathsf{based}\mathsf{on}\mathsf{the}\mathsf{type}\mathsf{of}\mathsf{variables}j\mathsf{and}k.\hfill \\ \hfill & \text{1:2}\mathsf{Same}\mathsf{as}\mathsf{Algorithm}1.\hfill \\ \hfill & 3.\mathsf{Set}{\widehat{r}}_{jk}={\tilde{F}}^{-1}({\widehat{\tau }}_{jk},{\widehat{\Delta }}_j,{\widehat{\Delta }}_k),\mathsf{where}{\tilde{F}}^{-1}\mathsf{is}\mathsf{the}\mathsf{trilinear}\mathsf{interpolation}\mathsf{of}{F}^{-1}\hfill \\ \hfill & \mathsf{using}\mathcal{G}.\hfill \end{array}$$

We next present a hybrid scheme to prevent interpolation in regions with high approximation errors. From Theorems 3 and 4, the approximation error increases when (i) the proportion of zeros π₀ increases and (ii) the absolute value of latent correlation r is large, i.e., large absolute values of Kendall’s Τ. However, the range of $\widehat{\tau }$ values is directly affected by π₀ since sign(x_ij – x_{i′ j})sign(x_ik – x_{i′ k},) = 0 in (1) for all pairs (i, i′) with zero values. That is, a higher π₀ leads to a smaller range of $\widehat{\tau }$. We derive upper bounds on the values of $\widehat{\tau }$ as a function of π₀ and use these bounds to define the boundary region for interpolation.

Let $\mathbf{x}\in {\mathbb{R}}^n$ and $\mathbf{y}\in {\mathbb{R}}^n$ be the observed n realizations of truncated continuous and continuous variable, respectively. The upper bound on the range of Kendall’s Τ can be obtained by enumerating the number of pairs between zero values. Let π₀ = n₀ / n where $n_0=\sum _{i=1}^{n}I(x_i=0)$ is the number of zero values out of n. Then from (1),

$$\mid \widehat{\tau }(\mathbf{x},\mathbf{y})\mid \le \left\{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)-\left(\begin{array}{c}\hfill n_0\hfill \\ \hfill 2\hfill \end{array}\right)\right\}∕\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)\le 1-\frac{n_0(n_0-1)}{n(n-1)}\approx 1-{\pi }_0^2.$$ (8)

Similarly, we can approximate the range of Kendall’s Τ for other data type combinations (see the Supplementary Materials). In summary, we obtain the following approximate bound (ABD) on the range of $\mid \widehat{\tau }\mid$ values

$$\text{ABD}=\{\begin{array}{cc}1-({\pi }_0{)}^2\hfill & \text{for TC case}\hfill \\ 1-{\left\{\max ({\pi }_{0x},{\pi }_{0y})\right\}}^2\hfill & \text{for TT case}\hfill \\ 2{\pi }_0(1-{\pi }_0)\hfill & \text{for BC case}\hfill \\ 2\text{min}({\pi }_{0x},{\pi }_{0y})\left\{1-\max ({\pi }_{0x},{\pi }_{0y})\right\}\hfill & \text{for BB case}\hfill \\ 2\max ({\pi }_{0y},1-{\pi }_{0y})\{1-\max ({\pi }_{0y},1-{\pi }_{0y},{\pi }_{0x})\}\hfill & \text{for TB case}\hfill \end{array}\phantom{\}}$$ (9)

If the value of $\mid \widehat{\tau }\mid$ is close to ABD, this indicates a high value of zero proportion and a high value of correlation. To prevent high approximation errors, we propose to apply linear interpolation if $\mid \widehat{\tau }\mid \le 0.9\text{ABD}$, and to use the original estimation approach otherwise. We call this the hybrid multilinear interpolation with boundary (MLBD) algorithm (Algorithm 3).

Algorithm 3 Multilinear interpolation with Boundary (MLBD) method

$$\begin{array}{cc}\hfill & \mathrm{Input}:\mathsf{Pre}\text{-computed values}{F}^{-1}({\tau }_l,{\Delta }_m,{\Delta }_q)\mathsf{on}\mathsf{a}\mathsf{fixed}\mathsf{grid}({\tau }_l,{\Delta }_m,{\Delta }_q)\in \mathcal{G}\hfill \\ \hfill & \mathsf{based}\mathsf{on}\mathsf{the}\mathsf{type}\mathsf{of}\mathsf{variables}j\mathsf{and}k.\hfill \\ \hfill & \text{1:2}.\text{Same}\text{as}\text{Algorithm}1.\hfill \\ \hfill & 3.\mathsf{if}\mid {\widehat{\tau }}_{jk}\mid \le 0.9\text{ABD}\text{in}(9),\text{apply ML Algorithm}2.\hfill \\ \hfill & \mathsf{if}\mid {\widehat{\tau }}_{jk}\mid >0.9\text{ABD},\text{apply ORG Algorithm}1.\hfill \end{array}$$

We use the same grid for both Algorithms 2 and 3, it is implemented in the R package mixedCCA. The detailed description of the grid is in the Supplementary Materials.

4. Performance Assessment

We assess the approximation quality and computational speed of three algorithm for latent correlation estimation: the ORG method summarized in Algorithm 1, the multilinear interpolation scheme (ML) in Algorithm 2, and the hybrid MLBD scheme in Algorithm 3.

4.1. Approximation accuracy of latent correlation estimation

We first focus on the approximation accuracy in computing latent correlations. We treat the correlations computed by the ORG approach as gold standard and evaluate the maximum value of the absolute difference with the latent correlation estimates using the two approximation schemes, ML and MLBD.

4.1.1. Comparison on simulated data

To assess the approximation accuracy in simulations, we generate two variables using five types combinations: TC, TT, BC, BB, and TB. Here we present results for the TC case, other cases are available in the Supplementary Material. First, we generate two Gaussian variables of sample size n = 100 with mean 0 and fixed value of latent correlation (we consider nine values from 0.05 to 0.91). Given the zero proportion value π₀ (we consider eleven values from 0.03 to 0.95), we shift both variables so that the truncation applied at zero leads to desired value of π₀. That is, we truncate one of the variables by zeroing all negative values that remain after the shift.

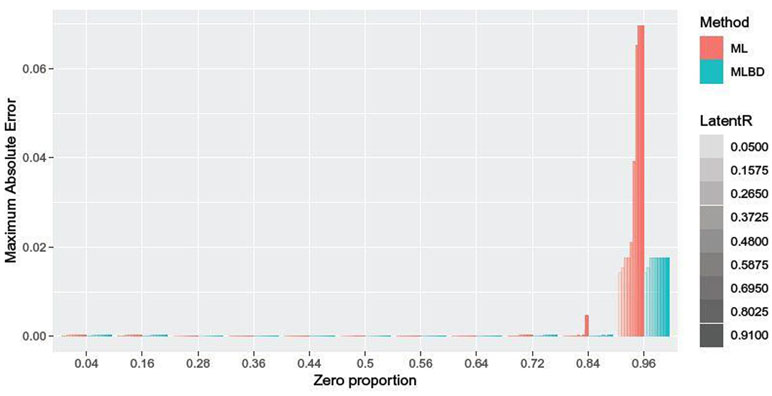
Figure 3 shows the maximum absolute error between the approximated values using interpolation and the gold standard values estimated by optimizing inverse bridge function across 100 replications. In Figure 3, the highest maximum absolute error for the ML method is 0.0406 at latent r = 0.91 and zero proportion rate π₀ = 0.95, respectively. The MLBD method reduced the error to 0.0101. When π₀ = 0.858, ML’s maximum error is only 0.0022. All other maximum absolute errors are less than or equal to 0.0004 and, on average, 0.0002, thus suitable for downstream statistical inference.

Fig. 3.

TC case. Maximum absolute error of multilinear interpolation approach (ML) and hybrid estimation approach (MLBD) for two simulated variables of sample size n = 100 across 100 replications. One variable is truncated continuous with zero proportion levels from 0.04 to 0.96 (T) and the other variable is continuous (C).

In summary, the approximation error for the TC case increases with the increase in zero proportion. However, the MLBD method accounts for the extreme cases, leading to significantly smaller approximation error compared to ML. The results for TT, BC, BB, and TB cases are similar (Supplementary Material). The approximation error increases with the increase in proportion of zeros for the truncated variable. The approximation error also increases as the binary variable gets more unbalanced in the number of zeros and ones. In all cases, the approximation error for the MLBD method is better compared to ML method.

4.1.2. Comparison on real data

We next consider three real-world data sets. The first data set is a subset of the quantitative microbiome profiling data (QMP), put forward in Vandeputte et al. (2017), which comprises n = 106 samples across p = 91 bacterial genera, resulting in a 91 by 91 latent correlation matrix estimation problem. The second data set is taken from the American gut project (AGP) (McDonald et al., 2018) and comprises filtered amplicon data for p = 481 operational taxonomic units (OTUs) across n = 6482 samples. Both microbiome data sets are treated as truncated continuous, and we use the inverse bridge function for the TT case. The final dataset is based on multi-view data from TCGA-BRCA (the cancer genome atlas breast invasive carcinoma) project, comprising gene expression data of 891 genes and micro RNA data of 431 micro-RNAs across 500 samples. The gene expression data are treated as continuous, and the micro-RNA data as truncated continuous. The latent correlation matrix for the gene expression data (of size 891 by 891) can be calculated using the explicit form of the inverse bridge function for the CC case. The correlation matrix estimates between micro-RNAs and genes (of size 431 by 891) and between micro-RNAs (of size 431 by 431) are calculated using the TC and the TT inverse bridge functions, respectively. The entire latent correlation estimate is of size 1322 by 1322 (891 + 431 = 1322).

We observed that, in the QMP and AGP data, there are no pairs of variables outside of our boundary specification (9), implying that ML and MLBD give identical estimates. In the micro-RNA data in TCGA-BRCA, six pairs of variables are outside of the specified bounds. We observed that maximum absolute error between ML (and MLBD) to the gold standard is 0.0006 on both the QMP data and the AGP data. The maximum error for MLBD on the TCGA-BRCA data is 0.0005. MLBD’s mean absolute error is 8.0e-05, 7.3e-05, and 1.1e-05 on QMP, AGP, and TCGA-BRCA data, respectively.

4.1.3. Comparison for graphical model estimation

We next assess the MLBD scheme in the context of sparse graphical model estimation with SPRING (Semi-Parametric Rank-based approach for INference in Graphical model) (Yoon et al., 2019). SPRING uses latent correlation estimation followed by neighborhood selection (Meinshausen and Bühlmann, 2006) to estimate sparse graphical models from quantitative and relative microbial abundance data. SPRING selects the optimal tuning parameter λ level via the Stability Approach to Regularization Selection (StARS) (Liu et al., 2010) which requires repeated subsampling of the data to estimate edge selection probabilities and thus repeated latent correlation matrix estimation.

To assess MLBD’s approximation accuracy, we measured the absolute difference of the entries in the estimated sparse partial correlation matrices between ORG and MLBD across two different regularization paths (λ-paths). We set the number of subsamples to 50. We first considered a fixed λ-path with 50 values log-linearly spaced in the interval [0.006,0.6] for both schemes. At the StARS-selected λ_StARS, we observed a maximum absolute difference of 0.0010 and mean difference of 7.4e-06, respectively, in the resulting partial correlation estimates. We also used a data-driven regularization path comprising 50 λ values, log-linearly spaced in [0.01σ_max, σ_max] where σ_max is the largest off-diagonal element in the respective latent correlation estimates (σ_max = 0.8183 for ORG, and σ_max = 0.8186 for MLBD, respectively). At the StARS-selected λ_StARS value, we observed a maximum difference of 0.0011 and a mean error of 7.8e-06 in the resulting partial correlation estimates.

4.2. Computational Speed-up

We report the numerical run times and highlight the speed-up of our approximation scheme on all described test scenarios. Run times are measured using the microbenchmark R package on a Linux system with Intel(R) Xeon(R) CPU E5-2680 v4 @ 2.40GHz. Table 1 presents run time results (in microseconds (μs)) for the synthetic data scenarios. Here, we consider pairs of simulated variables for all five data type combinations.

Table 1.

Run time (in microseconds [μs]) for latent correlation estimation across variable pairs (C - continuous, B - binary, T - truncated).

	TC	TT	BC	BB	TB
ORG	3767.28	24255.43	2516.40	2894.14	2177.13
ML	350.72	454.88	352.73	446.21	452.80
MLBD	362.72	479.92	368.92	483.67	493.77

The run time of the ORG method is highly data type dependent. For instance, the TT case, which is relevant for amplicon, Chip-Seq, or single-cell data, has the longest run time (~ 24255 μs ) due to the four-dimensional normal cdfs in its bridge function. Here, the ML and MLBD methods achieve a speed-up of about 50x. For the other cases, both approximation schemes achieve a 4x-10x speed-up compared to the direct optimization scheme. As expected, the run time of the hybrid MLBD scheme is longer than ML but allows tight control of approximation errors when estimated Kendall’s Τ values fall outside the boundary (see (9)).

Table 2 shows the run time results for latent correlation and graphical model estimation. For comparison, we also include run time results for computing Kendall’s Τ matrix using cor.fk function in R package pcaPP. We observe that MLBD achieves significant speed up of between 8x for the TCGA-BRCA data to more than 60x on the QMP data. In addition, MLBD’s computational cost is comparable to plain Kendall’s Τ calculation for the AGP and QMP data, and is only 1.2x slower on the TCGA-BRCA data.

Table 2.

Run time (in seconds [s]) for latent correlation estimation on biological data.

	latent correlation			SPRING on QMP
	QMP	AGP	TCGA-BRCA
ORG	59.63†	3459.05§	2039.52§	1810.39§
MLBD	0.97*	320.56†	245.13†	68.06§
Kendall	0.94*	318.09†	200.27†

^*: median value over 100 repetitions and

^†: median value over 10 repetitions, and

^§: one time result.

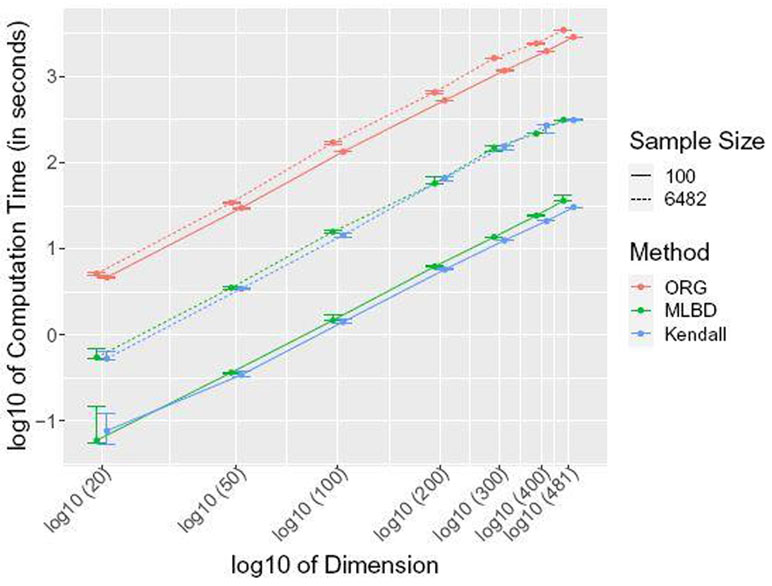
We next investigate the run time scaling behavior of the ORG, MLBD (using the TT case), and Kendall’s estimators with increasing dimensions p = [20, 50, 100, 200, 300, 400] at two different sample sizes n = 100, 6482 using the AGP data. Figure 4 summarizes the observed scaling in a log-log plot. For all methods we observe the expected O(p²) scaling behavior with dimension p, i.e., a linear scaling in the log-log plot. However, MLBD is at least one order of magnitude faster than ORG and comparable in run time to standard Kendall’s Τ independent of the dimension of the problem.

Fig. 4.

Computational scaling of the run time (median and standard deviation in log10 scale, in seconds) versus dimension p (in log10 scale) for the original optimization method (ORG, two repetitions), the proposed hybrid multi-linear interpolation method (MLBD, TT case, ten repetitions), and Kendall’s Τ (Kendall, ten repetitions). The Amplicon data from AGP is used for two different sample sizes, n = 100 (solid) and n = 6482 (dotted). All methods show the expected O( p² ) complexity as reflected in the linear run time increase with slope ≈ 2 in the log-log plot. MLBD is one order of magnitude faster than ORG and comparable in run time to standard Kendall’s Τ.

5. Discussion

We have introduced a fast method for computing latent correlations for variable pairs of continuous/binary/truncated types. The method is implemented in the R package mixedCCA and allows the estimation of latent correlations at a computational cost that is similar to standard Kendall’s Τ computation. Several improvements of the method can be pursued. First, the hybrid MLBD method uses a boundary condition $\mid \widehat{\tau }\mid >0.9\text{ABD}$. However, the constant 0.9 can be adapted for specific variable combinations (TT, TC, TB, BB or TT). Our simulation studies (Supplementary Material) suggest that a stricter boundary (lower constant) may be needed for the BC case to achieve similar approximation error as for the TC case. Another alternative is to use a boundary based on the zero proportion value only. However, this is a conservative approach as it ignores the dependence of approximation error on the size of the latent correlation. For example, if the latent correlation r = F⁻¹(τ, Δ) is very close to 0, the bound in Theorem 3 is not as large for the same value of zero proportion as when ∣ r ∣ is close to one. Secondly, motivated by the need for fast and accurate methods for processing modern high-dimensional sequencing data, we have focused here on processing sparse, highly skewed count or binary data. For ordinal variable types (Quan et al., 2018; Feng and Ning, 2019), which also have non-trivial bridge functions, our interpolation approach will likely also achieve faster latent correlation computation. Finally, in its current form, our hybrid multilinear interpolation scheme requires storing pre-computed function values on a large grid of points. An alternative potentially fruitful approach is to construct a closed-form analytical function that approximates the inverse bridge function directly, thus completely eliminating the grid. The shape of the inverse bridge function for the TC case (Figure 1) suggests that sigmoid log-logistic approximation functions (Kyurkchiev and Markov, 2015, Chapter 3) could be promising candidates, since they can adapt their smoothness to mimic the observed change from the sinusoidal function (zero proportion is equal to zero in Figure 1) to the step function (zero proportion is equal to one). We leave these investigations for future research.