Figure 7.

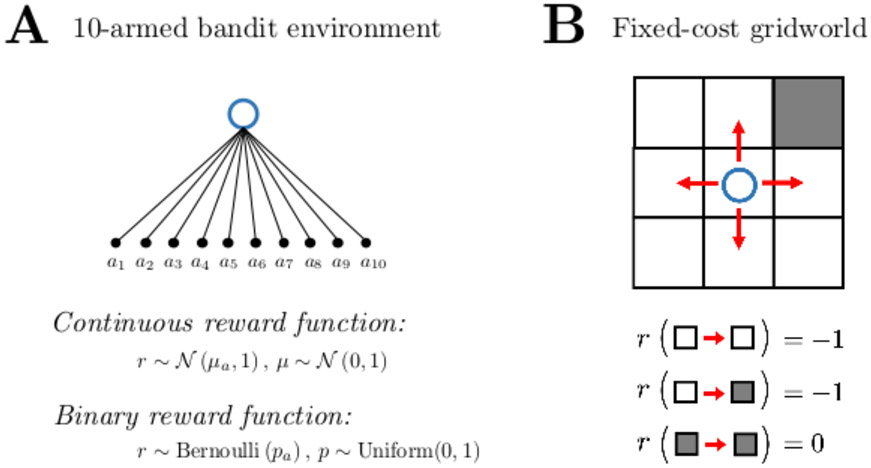
(A) The ten-armed bandit choice environment. At each timestep, the agent (blue circle) chooses one of ten options (‘arms’; black circles), and receives a reward that depends on which arm is chosen. The agent’s goal is to maximize its total reward. We simulated two reward functions: for continuous rewards, we used a Gaussian reward function such that a chosen arm a pays out a reward r according to a Gaussian distribution with a mean μ_a and a standard deviation of 1. The mean of each arm was initialized at the start of each simulation as a draw from a unit normal distribution. For probabilistic (binary) rewards, we used a Bernoulli function such that a chosen arm pays out either 0 or 1 according to an arm-specific probability p_a drawn from a unit uniform distribution. Each arm’s payout mean/probability was stationary over time within a simulation. (B) A fixed-cost 3x3 gridworld environment. At each step, the agent moves in one of the four cardinal directions (red arrows). The terminal state (grey square at top right) is absorbing. Once it reaches this state, the agent remains in place (self-transitions) for one timestep before the episode ends. Actions that would take the agent out of the gridworld (e.g., moving left from the leftmost states) are not permitted. The agent receives a reward of −1 for all state transitions except for self-transitions in the terminal state, which produce a reward of 0. To maximize reward, the agent must therefore learn to move in as few steps as possible from its initial state (randomized in each simulation) to the terminal state.