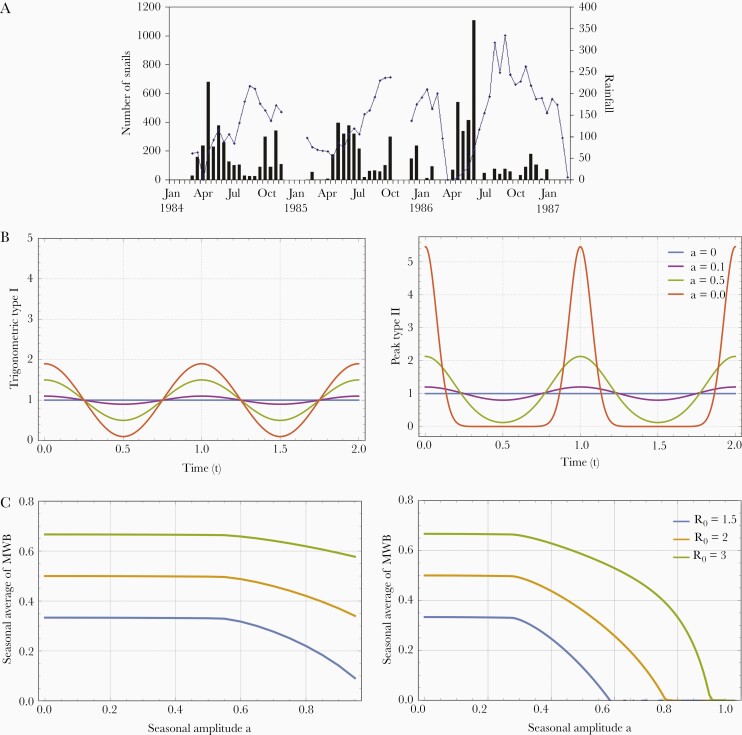
Figure 1.

A, Rainfall data (solid bar) and snail population numbers collected in the Msambweni region of eastern Kenya from March 1984 to January 1987 [3, 22]. B, Examples of type-I (left) and type-II peak (right) seasonality with amplitude parameter $a$. The type-I seasonality was modeled by trigonometric function, $1+a\cos \left(2\pi t\right)$, and type-II seasonality was modeled by an elliptic theta function of amplitude $0\le a<1$, $1+2\underset{n=1}{\sum ^{\mathrm{\infty }}}{a}^{n^2}\cos \left(2\pi nt\right)$. At small amplitude, $a$, both types are approximately equal, because higher-order Fourier modes become negligible. But as amplitude increases, they depart significantly in their variability (finite for type I and unlimited for type II). C, Seasonal average of mean worm burden (MWB), $\overline{w}\left(a\right)=\langle w^{\ast }(t,a)\rangle$ as a function of amplitude, $a$, for human-snail Macdonald systems Equation (4) for 3 values of basic reproduction number $R_0$ (transmission intensity), $R_0=1.5;2;3$. Left, results for a type-I trigonometric $N(t,a)$ model; right, results for a type-II peak $N(t,a)$ model. The curves indicate that for a lower $R_0$ and a higher seasonal amplitude, transmission becomes unsustainable in both type-I and type-II models. Not shown, these curves also depend on snail mortality, which in the case shown was $\nu =4$.