Modulus of elasticity of human periodontal ligament by optical measurement and numerical simulation

Abstract

Objective:

To determine the elastic modulus of the periodontal ligament (PDL).

Materials and Methods:

This study was carried out on eight human maxillary jaw segments containing central incisors. Displacements were measured under load using a laser sensing system, electronic speckle pattern interferometry (ESPI). Subsequently, finite element models presenting the same individual geometry as the respective autopsy material were developed by the software of Mimics and Ansys, based on scanning data from micro computed tomography (micro CT), to simulate tooth mobility numerically under the same force systems as were used in the experiment. Numerical force/deflection curves obtained from the models were fitted to the experimental curves by repeatedly calculating theoretical tooth deflections and varying the elasticity parameters of the human PDL.

Results:

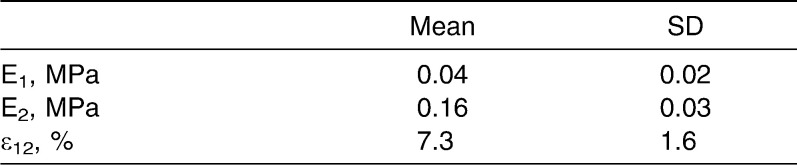
A bilinear material parameter set was assumed to simulate tooth deflections. Mean values of E₁  =  0.04 MPa, E₂  =  0.16 MPa, and ultimate strain of ɛ₁₂  =  7.3% were derived for the elastic behavior of the PDL.

Conclusion:

Force/deflection curves from the measurements showed a significant nonlinear behavior of elastic stiffness of the PDL. A bilinear material parameter set was suitably assumed to be a description of nonlinear properties of the PDL.

INTRODUCTION

As an important tissue of the periodontium, the periodontal ligament (PDL) is the most deformable component and is mainly responsible for tooth mobility. It transmits functional and orthodontic forces to the alveolar bone. It is believed that resulting stresses or strains within the PDL and bone control the bone-modeling process.1–4 Also with the development of modern stomatology, geometrical and biomechanical simulation models of the stomatognathic system are widely applied in oral clinical and research work, and higher simulation of the anatomy and biomechanical character of a stomatognathic system is required more greatly.

However, the elastic properties of the PDL, as published in former studies, show broad variation. Values for the elastic modulus, as stated in the literature, differ by a factor of 10⁵.5–7 This variation in results can be attributed to the complex structure of the PDL and the different modeling assumptions for the mechanical behavior resulting from this. Additional reasons for the variation in elastic properties include the differing study designs, especially with respect to experimentation.

Despite the fact that the PDL is known to be composed of a nonlinear viscoelastic material, most of the previous finite element (FE) models incorporate homogeneous, linear elastic, isotropic, and continuous PDL properties.8,9 And most FE studies in orthodontics have been performed with respect to data from models obtained by conventional computed tomography (CT). The PDL space is barely visible at most. Recently, it turned out that especially the boundary between the tooth and its socket, occupied by the PDL, has much better visibility on micro CT images. SkyScan-1172 Micro-CT (SkyScan, Brussels, Belgium), which was used in this study, allows us to reach a spatial resolution of 5 µm, corresponding to a nearly 1 × 10⁻⁷ cubic mm voxel size.

The aim of the present study was therefore to investigate the elastic modulus of the PDL with individual geometry and nonlinear properties by optical measurement and finite element analysis (FEA) simulation based on scanning data from micro CT.

MATERIALS AND METHODS

Experimental

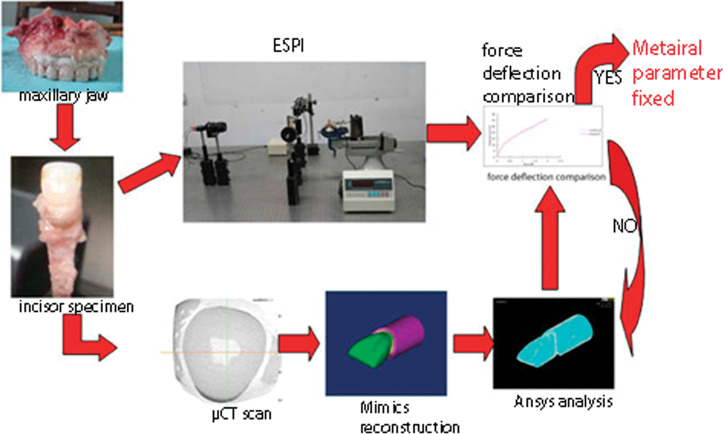
This study was reviewed and approved by the Research Ethics Committee of Shandong University Dental School. Eight human maxillary jaw segments containing one incisor were collected and were kept frozen at −20°C up to the start of the experiments. The combined experimental and computational method is illustrated in Figure 1. The procedure consisted of matching the force/deflection curve obtained from optical measurement and numerical simulation, after the set of micro CT scans was obtained. In this way, the numerical force/deflection curves were fitted to the experimental curves by repeatedly calculating theoretical tooth deflections and varying the parameters describing the nonlinearity. Detailed experimental and computational methods are described later.

Figure 1.

The combined experimental and computational method begins with a tooth specimen. A force/deflection curve is achieved from an optical measurement before micro CT scanning. A computational simulation of loading on the tooth is performed using the finite elements model generated from micro CT scans. The resulting computationally determined force/deflection curve is in accordance with an experimentally measured force/deflection curve in terms of various parameters of PDL FE models.

Optical Measurement of Initial Tooth Displacement

Specimens were first mounted in a block of YY0270-2003 resin (Shanghai Dental Instrument Factory Co, Ltd, Shanghai, China) to provide stable fixation within the experimental setup (electronic speckle pattern interferometry [ESPI]) (Figure 2).

Figure 2.

The ESPI apparatus was applied to evaluate initial tooth displacements under orthodontic forces. The ESPI apparatus and its schematic diagram.

The ESPI system has been developed and applied to qualitative and quantitative evaluations of initial tooth displacements under orthodontic forces.

Forces were delivered by applying lead weights perpendicularly to the titanium angle extended from the subject tooth. The angle was welded to the titanium crown embracing a maxillary central incisor, and the lingual screen was bonded to the lingual side. The labial surface of the angle and the lingual screen were positioned parallel to the long axis of the tooth and were checked for perpendicularity with the ground by using a leveling instrument to keep the direction of the force constant during measurements.

The ESPI apparatus measured translated displacement of the teeth during the process of loading in a manner described briefly as follows. A 632.8-nm helium-neon laser beam (10 mW) was passed through a collimating lens and split into two beams of equal intensity. One beam (reference beam) was directed toward a reference plane, and the other beam (sample beam) was directed toward the lingual screen of the specimen. A charge coupled device (CCD) video camera captured images from the specimen. The reference beam was directed in such a way that it intersected the path between the specimen and the video camera. A partial mirror deflected the reference beam into the video camera, causing it to interfere with the light reflected from the specimen. Because of the monochromatic properties of the laser light, the specimen and reference beams constructively or destructively combined to produce a speckle pattern of fringes over the lingual screen. The speckle images were recorded by the CCD video camera, were digitized, and were stored in a computer. Out-of-plane displacement was calculated using the following equation:

where λ was the wavelength of the laser (632.8 nm) and n was the number of fringes observed in the speckle pattern.

Preliminarily, the point of application of the force passing through the center of resistance at which translation could be produced without rotation was investigated by calculating tooth displacement from the speckle pattern of fringes in real time with translated retraction (Figure 3). Then the tooth was experimentally translated, and its displacements were measured when the magnitude of load was increased up to 2.0 N with 0.2-N steps. Each loading was performed for 3 seconds. Ten measurements were made and averaged. Force/deflection curves from these measurements were obtained.

Figure 3.

(a) The speckle pattern of fringes when the magnitude of load was 1.0 N. (b) The fringes when the load was increased with 0.2 N based on (a). Then the variation in the speckle pattern of fringes was calculated during tooth translation under orthodontic forces.

To assess the significance of the error involved in the optical measurement methods, the authors reassessed a series of 4 subjects 2 months after initial measurements were taken. The mean difference between the first and second measurements, the standard error of a single measure, and the percentage of total variance attributable to measurement error were calculated for each variable. Error variance was calculated using the following formula:

where x₁ and x₂ are the measurements repeated and n is the sample size. The mean differences were less than 0.1 µm.

Model Generation

A CT image stack from the same subject was registered with the micro CT data for tooth and bone segments (Figure 4). Standard imaging conditions include a tube voltage of 80 kV and a tube current of 100 µA, a spatial resolution of 13 cubic µm voxel sizes, and a slice thickness of 13 µm. Then the images were imported into the software Mimics (Materialise, Leuven, Belgium). A semiautomatic approach involving threshold and manual refinement in combination with several three-dimensional (3D) operations allows for segmentation of the PDL mask. Once the PDL mask had been segmented, it was applied to the CT images to separate tooth from bone.10 The segmentation was exported to analysis software Ansys (ANSYS Inc, Canonsburg, Pa) input file format by the exporting functionality in Mimics. The tooth, PDL, and alveolar were modeled with 10-noded tetrahedral solid 92 elements. Final preprocessing and postprocessing were performed in an Ansys solver that was used for the solution.

Figure 4.

The specimens underwent 13-µm very high-resolution CT scans using a SkyScan 1172 scanner. (A) System SkyScan 1172 Micro CT scanning for tooth samples. (B) The tooth sample inside the holder box of the micro CT.

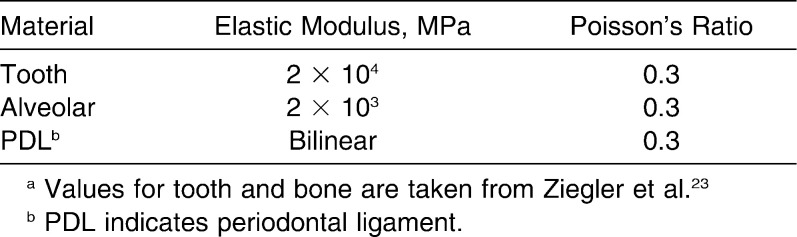
As a boundary condition, the nodes on the exterior side of the alveolar were fixed. “Bone” and “tooth” elements were assigned constant linear elasticity parameters for all calculations (Table 1), whereas PDL elements were assigned a standard set of parameters derived from experiments on pig teeth only in the first calculation, respectively.11 In contrast to the parameters for tooth and bone, these parameters described nonlinear material characteristics: Two different values for the elastic modulus were used, and a value for the ultimate strain ε₁₂ was specified to simulate bilinear material characteristics with a more elastic initial phase and a less elastic secondary phase, which was subject to the higher elastic modulus.

Table 1.

Material Parameters of Tooth, Bone, and Periodontal Ligament Used in This Study^a

Determination of Elastic Modulus of the PDL

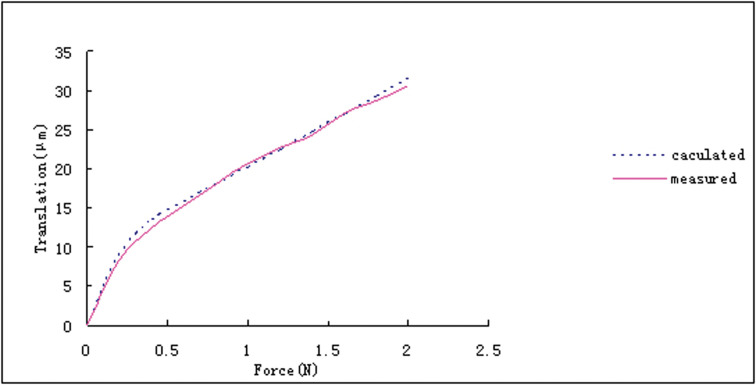
This FE model was now numerically loaded with the same force as the corresponding tooth during the experiment. Numerical force/deflection curves obtained from the models were fitted to the experimental curves by repeatedly calculating theoretical tooth deflections and varying the elasticity parameters of the human PDL (Figure 5). An individual set of parameters consisting of two elastic modules and one ultimate strain was derived for each of the eight finite element models.

Figure 5.

Fit of the calculated translation to the measured curves based on bilinear mechanical behavior of the periodontal ligament.

RESULTS

The eight 3D finite element models of the maxillary incisor with the PDL and the alveolus are successfully shown in Figure 6. After 3D meshing, the mean results of eight models show 115,280 nodes and 80,883 10-node-tetrahedral elements. The accuracy of the models was very high, and the models can be observed from any view. Because the bony structure of the models had only a negligible influence on initial tooth movement under consideration in the present study because of its relatively high Young's modulus, surrounding cortical bone was idealized and was given a cylindrical shape.12,13

Figure 6.

Tooth-PDL-alveolar FE models were reconstructed in the software of Ansys. (A) Tooth-PDL-alveolar FE models. (B) Alveolar FE models. (C) Tooth FE models. (D) PDL FE models.

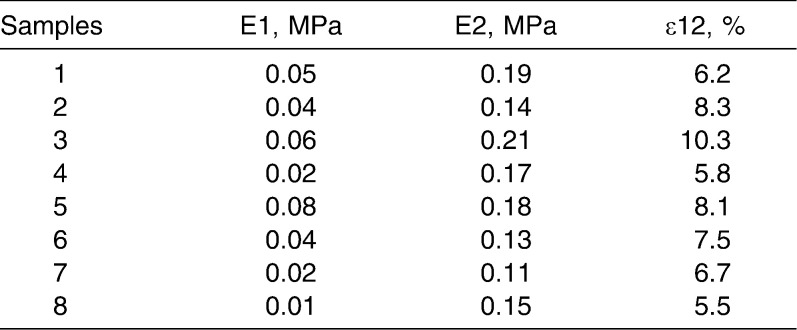
The elasticity parameters providing the most realistic simulation of tooth movement in each model are summarized in Table 2. Mean values and standard deviations are shown in Table 3. The elastic modulus E₁ of the initial expansion phase ranged from 0.01 to 0.08 MPa, with a mean value of 0.04 MPa (SD  =  0.02 MPa). Young's modulus E₂ of the second expansion phase ranged from 0.11 to 0.21 MPa, with a mean value of 0.16 MPa (SD  =  0.03 MPa). Borderline values between these two phases ranged from 5.5% to 10.3%, with a mean of 7.3% (SD  =  1.6). The set of parameters derived from the mean values is to be used in future studies as the basis for simulations of the natural mechanical characteristics of PDL.

Table 2.

Elasticity Parameters of the Periodontal Ligament of All Specimens Determined by Fitting Theoretical Curves to Experimental Curves

Table 3.

Mean Values and Standard Deviations of Elasticity Parameters Recorded for the Periodontal Ligament

DISCUSSION

In the present study, the elastic modulus of the PDL was determined by contrary calculation in human subjects. This was found to be an effective and reliable method. A bilinear result can thus be carried out by feeding values of the elastic modulus of the PDL to the finite element model corresponding to the magnitude of the optical measurement. The values obtained in this study could contribute much to the development of dental biomechanics analysis.

On the basis of current results, the ESPI technology was well suited to evaluate tooth translation induced by loading through the center of resistance of the tooth. The single biggest advantage of ESPI was its ability to assess tooth deformation without physically contacting the tooth, and changes as small as 0.3 µm in tooth translation could be detected. ESPI provided the added advantage of being able to assess tooth displacement repeatedly on the same sample because of the nondestructive nature of the test.14

According to the literature, the accuracy and reliability of results in a model obtained by FE analysis are highly dependent on the geometry of the structure and the properties of its material.15 Although many studies have been performed to investigate the properties of periodontal tissues using the finite element method, most used coarse models and linear analyses16–18 in which low simulations for the anatomy and biomechanical character of the PDL were performed. Therefore, these results may be led to qualitatively wrong interpretations, not to mention the quantitative evaluation. In the present study, the FE models are based on a micro CT dataset providing detailed descriptions of both external geometry and internal morphology of alveolar bone. In addition, the use of automatic meshing software saves time compared with semiautomatic algorithms.19 In particular, the application of volume- and topology-preserving algorithms ensures that anatomically faithful models of investigated structures are obtained. Furthermore, a bilinear stress-strain relationship based on experimental results was chosen for modeling the PDL.

To reduce the number of equations to be solved, the teeth were not differentiated into enamel, dentine, pulp, and cementum but were provided uniformly with the elasticity parameters of dentine. In view of the minor forces applied, the influence of this simplification is negligible because no substantial deformation of the dental hard tissue was to be expected. For the same reason, the bone was not differentiated into cortical alveolus, cancellous bone, and cortical bone.12,13

Initial tooth mobility has been investigated in many theoretical and experimental studies.20,21 The nonlinearity of this initial movement has been known at least since the 1950s through clinical measurements carried out by Mühlemann.22 In this study, the computational approximation of the mechanical behavior of the PDL was carried out with a set of parameters that consisted of two differing elastic moduli and an ultimate strain. This approach has been used previously23,24 and allows a good level of computational approximation with the nonlinear force/displacement behavior of the tooth investigated. The two different phases of initial movement were classically interpreted, in that the periodontal fibers, which are curled when in a resting state, “uncurl” in the first, more elastic phase, and only then does their stretching, which is associated with low elastic properties, begin.25 Additionally, under the influence of notably higher forces, the bony structures and the tooth itself show minor elastic deformation. This is due on the one hand to the fact that collagenous fibers of the periodontal ligament have only a small range of elasticity, and on the other hand to the fact that periodontal tissue is compressible only to a limited degree.

However, the structure of the PDL was greatly complicated. It consisted mainly of collagen fiber bundles, cellular elements, and tissue fluids.26 The combined effects of tension on the fibrous elements and of compression on the fluids and cellular elements have been considered within the PDL for the tooth support mechanism under external forces.27 Therefore, it is not only the collagenous fibers that determine the elasticity parameters of the periodontal ligament, but also hydrodynamic effects and the elasticity characteristics of all structures involved in this network.28 Thus, the two elastic moduli determined in this study do not describe the behavior of collagenous fibers in the periodontal ligament space, but rather a compound effect based on the behavior of several different structures.

CONCLUSIONS

• A bilinear material parameter set was suitably assumed to describe nonlinear properties of the periodontal ligament.

• The nonlinear characteristics of the periodontal ligament should be considered in future research based on an advanced computerized system, so more accurate mechanical simulation of material characters can be achieved.