Inclusion of Effect Size Measures and Clinical Relevance in Research Papers

Abstract

Background:

There are multiple issues that arise when researchers focus on and only report “statistical significance” of study findings. An important element that is often not included in reports is a discussion of clinical relevance.

Objectives:

The authors address issues related to significance, the use of effect sizes, confidence or credible intervals, and the inclusion of clinical relevance in reports of research findings.

Methods:

Measures of magnitude, precision, and relevance such as effect sizes, confidence intervals (CIs), and clinically relevant effects are described in detail. Additionally, recommendations for reporting and evaluating effect sizes and CIs are included. Example scenarios are presented to illustrate the interplay of statistical significance and clinical relevance.

Results:

there are several issues that may arise when significance is the focus of clinical research reporting. One issue is the lack of attention to nonsignificant findings in published works even though findings demonstrate clinical relevance. Another issue is that significance is interpreted as clinical relevance. As well, clinically relevant results from small sample studies are often not considered for publication, and, thus, findings might not be available for meta-analysis.

Discussion:

Findings in research reports should address effect sizes and clinical relevance and significance. Failure to publish clinically relevant effects and CIs may preclude the inclusion of clinically relevant studies in systematic reviews and meta-analyses thereby limiting the advancement of evidence-based practice. Several accessible resources for researchers to generate, report, and evaluate measures of magnitude, precision, and relevance are included in this article.

Traditional formats for reporting research findings that focus heavily on statistical significance have come under increased scrutiny (Hayat et al., 2019; Kraemer, 2019; Pickler, 2019; Staggs, 2019; Wasserstein et al., 2019). In addition to highlighting statistical significance, there is a growing trend to include effect sizes and the clinical or practical relevance of findings in research publications (Hayat et al., 2019; Page, 2014). These reports become increasingly important in health care-related research as clinically relevant findings are translated for evidenced-based care. Despite these concerns, many researchers continue to report only statistical significance (Rosnow et al., 2000; Wasserstein et al., 2019). The purpose of this article is to discuss the usefulness of reporting effect size measures and addressing clinical relevance in research publications. Discussions include background related to the issues of reporting statistical significance and clinical relevance; measures of magnitude, precision, and relevance; hypothesis generating versus hypothesis testing designs; and issues with reporting clinically relevant findings. Finally, several scenarios will be presented that highlight the interplay between significant and clinically relevant findings.

Researchers and the scientific community have traditionally relied on p-values to determine the significance of research findings, yet there have been numerous flaws noted when using this as the sole approach to interpret and apply findings from research (Amrhein et al., 2019; Hayat et al., 2019; Pickler, 2019; Staggs, 2019; Wasserstein et al., 2019). Misuse of p-values led the American Statistical Association to release a statement clarifying the purpose and appropriate use and interpretation of p-values in research (Wasserstein & Lazar, 2016; Wasserstein et al., 2019). The traditional understanding of statistical significance as p < .05 is arbitrary, and misinterpretations have been noted when analysis is limited to calculating and interpreting p-values (Schober et al., 2018; Staggs, 2019; Wasserstein et al., 2019). Moreover, p-values will and are expected to change based on sample size, as larger samples are more likely to have smaller p-values (Staggs, 2019). Issues with relying solely on p-values to determine significance of findings are not new (Pickler, 2019); however, the exclusive reliance on statistical significance to assign meaningfulness and importance to research findings continues to be a pervasive problem throughout research literature and across numerous disciplines, including nursing (Kraemer, 2019; Polit & Beck, 2020).

Recommendations have been made to reduce emphasis on p-values and encourage researchers to incorporate other statistical values in research reports to aid in interpretation of findings (Hayat et al., 2019; Pickler, 2019; Schober et al., 2018; Wasserstein et al., 2019). Reporting effect sizes and confidence intervals (CIs) in research findings may help researchers in interpreting clinical relevance of study findings (Aarts et al., 2014; Kraemer, 2019; Schober et al., 2018). Explanations of findings in the context of clinical relevance, or minimally important change, add transparency and offer the reader a broader view of data-based evidence for knowledge and practice (Page, 2014; Polit & Beck, 2020). This is especially true when considering evidence-based practice (EBP) in health care. EBP is a combination of research evidence, clinical expertise, and a patient’s values and preferences (Teodorowski et al., 2019). Research reports that are strengthened with more informative results can support improved patient practices and outcomes. Among these are measures of magnitude, precision, and relevance.

Measures of Magnitude, Precision, and Relevance

A common focus of quantitative research is the estimation of a population parameter, representing some quantity of interest, based on data from a sample. These sample estimations are used as the basis for making inferences about the magnitude of that quantity of interest in the population from which the sample was selected. These sample estimates, or effect sizes, may be a measure of association or differences between groups or other comparative measures (See Table 1, adapted from Cumming, 2012, for specific examples). Including information in research reports about effect sizes and their clinical relevance, as well as measures of precision for the effect sizes, is critical to the development of a body of knowledge and to consideration in EBP guidelines. The next sections include discussions of concepts related to these measures of magnitude, precision, and relevance, including effect sizes, confidence and credible intervals, and clinically relevant effects.

Table 1.

Hypothetical Examples of Measures of Effect Size

Effect Size	Description	Example
Mean, M	Original units	Mean length of stay in hospital, M = 10 days.
Difference between two means	Original units	The average patient satisfaction increased last year by 0.5, from 3.1 to 3.6 in a 1 to 5 scale.
Median, Mdn	Original units	Median length of stay in hospital, Mdn = 5 days.
Percentage	Units-free	35.5% of patients were African American.
Frequency	Units-free	39 practices implemented a palliative care intervention.
Correlation, r	Units-free	Anxiety scores correlated with depression scores among patients (r = 0.6).
Standardized difference between two means, Cohen's d	Standardized	The average effect of psychotherapy was d = 0.68.
Regression weight, b	Original units	The slope of the regression line for income against age was b = $1,350/year.
Standardized regression weight, β	Standardized	The standardized β-weight for age in the regression was 0.23.
Proportion of outcome variance explained by a model, R2	Units-free	Three variables of age, education, and family status in the multiple regression together explained 48% of the variance of the outcome variable (R2 = .48).
Proportion of outcome variance explained by components of a model, partial ω2 (Greek omega-squared)	Units-free	The independent variable age accounted for 21% (partial ω2 = 0.21) of variance of the outcome variable after controlling for the other predictors.
Risk	Units-free	The risk that a child has a bicycle accident in the next year is 1/45 or 2.2%.
Relative risk	Units-free	A boy is 1.4 times as likely as a girl to have a bicycle accident in the next year.
Odds	Units-free	The odds of infarction among smokers are 2.02; the odds of infarction among non-smokers are 1.25
Odds ratio	Units-free	The odds of infarction among smokers are 1.6 times the odds among non-smokers
Number needed to treat, NNT	Patients	NNT = 14 indicated that 14 people need to be treated with Apixaban to prevent one case of recurrent thromboembolism

Effect Sizes

The magnitude of the quantity of interest in a research study is the effect size. For example, if attitudes or behaviors in a group of people are measured before and after an intervention, it is natural to think of the average change in attitude or behavior as an effect of the intervention, and the amount of change as the size of that effect. However, researchers use the term effect size more broadly; it does not have to be a change and there may not be explicit cause and effect. An effect is that quantity of interest (Cumming, 2012), i.e., the difference in group means or the correlation, or whatever measure that conveys the magnitude of the phenomenon of interest (Cohen, 1988, 1992). Therefore, an effect size is simply the amount of that quantity—or the magnitude of the effect. There are many different measures of effect size that can be described and classified in multiple ways. The choice of and interpretation of effect size is dependent on the specific statistical techniques used to address the study aims (e.g., a comparison of group means vs. a comparison of percentages may use different measures of effect size), as well as on specific contextual knowledge.

As shown in Table 1, some effect sizes are in the original or unstandardized units of the phenomenon of interest, while others are either units-free or standardized. Standardized effects, such as Cohen’s d, are used to compare several numerical variables with disparate units of measurement. Some units of measurement have intrinsic meaning, such as measurement scales for height, weight, temperature, or blood pressure readings, while others, such as measures of anxiety or depression, do not. In that case, standardizing effects may be more meaningful. Standardized effect sizes expressed in standard deviation units like “z” scores (Cumming, 2012) can be compared across studies or across different outcomes within the same study. Effect sizes—both unstandardized and standardized from individual studies—should be reported so they are available for inclusion in systematic reviews and meta-analyses. Further, all effect sizes—whether small or large, expected or unexpected—should be reported in the results of a study (American Psychological Association [APA], 2020).

As noted above, estimating unknown effect sizes in a population of interest is often a purpose of empirical research (Cummings, 2012). These estimates are sample effect sizes that are computed from samples. There is uncertainty in using sample effect sizes as estimates of corresponding population effect sizes. The degree of uncertainty of a sample estimate of an effect size is indicated by a range of possible population values for this effect size that are compatible with the observed sample data. The most common paradigms used in inferential statistics are the frequentist (classical) approach and the Bayesian approach (Efron & Hastie, 2016). A CI from the classical approach or a credible interval from the Bayesian approach are the most common forms of uncertainty ranges (Efron & Hastie, 2016).

CIs and Credible Intervals

CIs belong to the classical inferential statistics paradigm (Cumming, 2012) and, therefore, are currently more widely used and reported in the research literature. A CI is calculated around the sample estimate and provides a range of plausible values for the (unknown) population parameter. Applying CIs to effect sizes provides a range of plausible effect sizes in the population (Schober et al., 2018). The statement associated with a CI is that the researcher has a certain level of confidence (typically 95%) that the reported interval does contain the true value of the population parameter. The 95% is not the probability that the interval contains the true value; the interval either does or does not. Rather, the 95% indicates that if the study was repeated many times using randomly selected samples of the same size and from the same population, and a CI was computed from each of these samples; 95% of these hypothetical intervals would contain the true population value (Casella & Berger, 2002).

The width of the interval also provides information about the precision of the estimate. Narrower CIs indicate more precision in the population parameter estimate. It may be more important for researchers to consider the width of the interval, that is, the precision of the estimate it represents, rather than to only consider whether or not the interval includes the null value (Wasserstein et al., 2019). Amrhein et al. (2019) argue that the term “compatibility” is a better concept for interpretation of the interval than “confidence.” The interval shows the plausible true effect sizes most compatible with the sample data, under the assumptions used to compute the interval.

A credible interval is the Bayesian statistical alternative of the CI. It is the interval in which an unobserved parameter has a given probability of inclusion. In contrast to a classical CI, it is correct to interpret the credible interval as one with a given probability (again, typically 95%) of containing the true value of the population parameter (Makowski et al., 2019). As the Bayesian statistical paradigm becomes more widely used, it will be important for researchers to understand the difference in interpretations for a CI versus a credible interval.

Clinically Relevant Effects

Researchers have attempted to define clinical relevance (i.e., clinical significance, clinical importance, practical importance) as an indication of whether findings from research are meaningful for clinicians and patients, and whether the effects or benefits justify costs and risks (Armijo-Olivo, 2018; Ferreria & Herbert, 2008). An important issue for researchers to consider is what magnitude of observed effect would be deemed “clinically relevant.” This is a far more complex question than it may appear. First, while there are published guidelines for interpreting several effect size measures as “small,” “medium,” and “large” (Cohen, 1992), the effect size that is clinically relevant depends on the specific outcome measure and a specific context. A researcher must ask the question, “What change in the given study outcome is meaningful or important?” For example, what magnitude in the difference in mean weight or HbA1C or systolic blood pressure (SBP) between an intervention and control/usual care groups would be large enough to recommend a change in clinical practice? In hypothesis-generating studies, a researcher must decide what magnitude of effect in the outcome would warrant further exploration.

A second important point is what constitutes a clinically relevant effect for a given outcome may differ by population or even individual. For example, a 1-lb (0.45 kg) weight loss in adults would rarely be of clinical importance but a 1-lb weight loss in infants weighing 10 lb (4.54 kg; i.e., a 10% loss in weight) would be clinically relevant. The concept of individualized (precision) medicine implies the examination of relevance in a single patient. This method of decision-making is sometimes utilized in fields of medicine in which risks are considered high such as oncology (Vitali et al., 2019).

While the clinical relevance of effect sizes for specific outcomes can differ by population, there are situations in which effect sizes and clinical relevance can be applicable among various populations and disease processes. For example, Farrar et al. (2001) reviewed 10 clinical trials examining the effect of pregabalin on chronic pain. Study designs and outcome measurements were similar across trials. The authors found a consistent relationship between the outcome measures within and across studies, where a 30% reduction in reported pain intensity was a clinically relevant difference. This finding held across studies regardless of underlying disease process or treatment group and supports the practice of identifying and evaluating effect sizes for outcome measures that can be used across studies (Farrar et al. 2001). When attempting to estimate an effect size based on multiple studies, researchers may perform a meta-analysis.

Meta-Analyses

Meta-analysis is a technique that allows evidence from studies (in both published and available unpublished literature) that address similar questions to be combined (Cumming, 2012). The strength of a meta-analysis is dependent upon the completeness and availability of study findings. Although studies with clinical relevance hold importance, they may not be included in meta-analyses if results are not significant, and thus lead to skewed results from the meta-analyses. This ultimately may limit the translation of research into practice. This may be especially true for studies with small or novel samples because of rare, fragile, or hard-to-reach populations that are difficult to enroll in research studies (Rice et al., 2020).

Using evidence from multiple studies enables synthesis—a way of weighted averaging— of the effect sizes. The combined effect size can provide strong evidence for EBP. Combining effect sizes from two or more studies can lend support to the credibility of the effect, provided the effect sizes broadly agree and are from studies that are largely independent and test the same hypothesis (Cumming, 2012). Further, combining CIs obtained from single studies can increase precision in synthesizing results. Effect sizes from multiple studies are included in collections such as the Cochrane Database of Systematic Reviews (www.cochranelibrary.com), which contains many meta-analyses specifically related to interventions in health care. If effect sizes from findings are not readily available or reported, researchers may opt to perform hypothesis-generating studies.

Hypothesis-Generating and Hypothesis-Testing Designs

Hypothesis-generating research provides exploratory information and justification for subsequent hypothesis-testing research (Kraemer, 2019). In hypothesis-generating studies, researchers look for patterns—not necessarily definitive answers (Biesecker, 2013) —and can discover clinically relevant findings that may potentially be translated to practice. Reports of hypothesis-generating research should always include effect sizes and CIs. In hypothesis-generating studies, it is not appropriate to report p-values if sample sizes and power to detect relationships or differences are not sufficient (Kraemer, 2019). Effect sizes from hypothesis-generating research provide preliminary information on the magnitude of an outcome and may be used to develop hypotheses (Biesecker, 2013).

In comparison, hypothesis-testing research provides empirical testing of a priori hypotheses and requires adequate sample sizes determined by power analyses (Hartwick & Barski, 1994; Kraemer, 2019; Polit & Beck, 2020), which in turn depend on the specific statistical techniques to be used, the respective measures of effect size, and tolerable margins of uncertainty about the observed estimates. Hypothesis-generating studies may be used to provide an a priori plausible range of effect size values to be used for sample size determination in hypothesis-testing research (Biesecker, 2013; Kraemer, 2019). Hypothesis-testing designs preceded by hypothesis-generating research work together to maximize resources and time (Biesecker, 2013). Translational research combines the paradigms of hypothesis-generating and hypothesis-testing research, and thus allows for the examination of the magnitude of the effect for clinical outcomes and clinical relevance—especially in small sample size studies (Aarts et al., 2014; Biesecker, 2013).

Issues with Reporting Clinically Relevant Findings

As trends towards reporting effect sizes continue, researchers should be aware of how clinical relevance affects the meaningful use of research studies. Standards for analysis and translation of exploratory and confirmatory research findings to clinical practice can guide the publication and use of clinically relevant findings (Melnyk & Fineout-Overholt, 2018). However, underlying issues related to study sample sizes, publishing recommendations, and individualized patient variability should be carefully considered when research and practice recommendations are made in research reports.

Small Samples and Individuality in Research

Examples of studies with small samples and/or limited access to participants include studies related to persons with rare diagnoses, hard-to-reach populations, orphan drugs, and genome studies (Biesecker, 2013; Hilgers et al., 2016; Rice et al., 2020). Regardless of small sample sizes, these studies may contribute to clinical knowledge despite low power and statistical nonsignificance. For example, recent advances in genetics and genomics have inspired research questions related to individual variability in the expression of disease and symptom management (Biesecker, 2013). Some researchers have made the case that calculations of effect sizes are necessary and meaningful in analysis of data on an individual level (Vitali et al., 2019) and can be used as a benchmark tool (along with accompanying standard deviation) in measuring individual treatment effects (Polit & Beck, 2020). These studies are more likely to employ hypothesis-generating designs rather than hypothesis-testing designs.

Failure to Publish Findings

Researchers, editors, and publishers often prioritize disseminating findings from hypothesis-testing studies rather than hypothesis-generating studies. Additionally, researchers and editors often fail to publish studies with nonsignificant findings (Amrhein et al., 2019), even when the findings have clinical importance. This becomes an issue in health care if clinicians only have access to published research and, thus, are not able to consider unpublished clinically relevant findings for practice, policy, and decision-making (Kraemer, 2019; McCartney & Rosenthal, 2000). Reports of clinically meaningful research can translate to clinically applicable evidence for practice (Teodorowski et al., 2019). Failure to publish nonsignificant findings, or failure to include measures of clinical relevance and precision, such as effect size and CIs, may have adverse consequences ultimately affecting patient care (Page, 2014).

Interplay of Statistical Significance and Clinical Relevance

There are several scenarios that may affect the reporting and interpretation of research findings. These scenarios include: (a) research findings are significant, but not clinically relevant; (b) research findings are clinically relevant, but not significant; (c) research findings are both clinically relevant and significant; and (d) research findings are neither clinically relevant nor significant. In this last scenario, researchers typically would not pursue publication. The following examples describe the first three scenarios in more detail.

Scenario 1: Statistical Significance Without Clinical Relevance

When research findings are significant but not clinically relevant, researchers should use caution when recommending changes to practice in research reports. For example, Ellison et al. (1989) found a decrease in SBP (−1.7 mmHg; 95% CI = −0.6, −2.9, p = .003) and diastolic blood pressure (−1.5 mmHg; 95% CI = −0.6, −2.5, p = .002) in high school students when changes were made to food purchasing and preparation practices. While the decrease was significant, a change of less than 2 mmHg may not be considered clinically meaningful, especially if the baseline BP is severely elevated. When study findings demonstrate statistical significance but little clinical relevance, care should be taken by researchers and clinicians to critically appraise the research study for generalizability and application to clinical practice.

Scenario 2: Clinical Relevance Without Statistical Significance

Conversely, researchers may consider recommendations in the context of personalized patient care when findings demonstrate clinical relevance but not statistical significance. These findings may be considered promising for replication in later studies and may hold importance for evaluation of future treatment and interventions, warranting further examination in health care research. Examples of studies reflecting hypothesis-generating findings of clinical relevance, and measures of effect sizes and CIs, are listed in Table 2. Each study listed contributed important new information to the literature surrounding populations that are both vulnerable and difficult to recruit into research studies. The works established effect sizes that would be considered clinically relevant for relationships among variables that had not been previously studied, thus providing direction for further research.

Table 2.

Small Sample Studies with Clinical Relevance

Authors	Population	Ages (years)	Study variables	N	Clinically meaningful effect sizes of relationships
Johnson et al., 2018	Brain tumor survivors	8-12	Child perceived stress, sleep-wake disorder (SWD), parent-reported fatigue; cancer-related fatigue (CRF)	21	CRF-child perceived stress; SWD-child perceived stress
Gray et al., 2020	Children with ADHD diagnosis	6-10	Child sleep and sleep hygiene, mother and father ADHD symptoms	27	child sleep hygiene, sleep onset latency, and night wakings-ADHD symptoms in one or both parents
Davis et al., 2019	Children with Type 1 DM	6-12	child perceived stress; child depressive symptom; maternal depressive symptoms; child’s perceived stress; HbA1c levels	30	child perceived stress-child depressive symptoms; child’s perceived stress and HbA1c
Soistmann, 2018	Children with sickle cell disease	8-14	Child fatigue; perceived stress; blood pressure; sleep; cortisol levels	30	Child fatigue-perceived stress; DBP-sleep; fatigue—sleep’ cortisol-sleep; cortisol-fatigue
Rice et al., 2018	Preschool children in day care and schools	3-5	Blood pressure, sex, geographical location, birth status, BMI, serum CRP; salivary cortisol	56	BP status — cortisol pm; BP status — birth status; BP-CRP; BP — cortisol

For example, intervention studies designed to improve sleep in children who have attention deficit/hyperactivity disorder (ADHD) may be influenced by the findings of Gray et al. (2020). Although not significant, researchers found a large effect (R² = .331), based on Cohen’s criteria (Cohen, 1992), between mother’s ADHD symptoms and child’s sleep onset latency, which suggests considering the effect of parent ADHD symptoms on child sleep. Additionally, while a single study with a small sample size should not direct health care recommendations, including such studies in meta-analyses can provide a more complex and nuanced interpretation of synthesized data from multiple studies.

Scenario 3: Clinical Relevance and Statistical Significance

In the last scenario in which findings show both clinical relevance and statistical significance, researchers may have more evidence on which to base future research and practice recommendations. This is especially true when meta-analysis demonstrates similar findings across multiple studies. An example of this is a study by Lynch et al. (2019) who examined the influence of psychological stress and depressive symptoms on body mass and central adiposity in 147 children 10–12 years old. In this study, depressive symptoms were reported by normoweight, overweight, and obese children. Significant and clinically relevant findings were noted between depressive symptoms and body mass and central adiposity, F (7, 139) = 7.925, p < .001, R² = .285). This finding suggests that in addition to further research examining depression as a factor in body mass and central adiposity, recommendations for clinical practice may include regular screening practices of BMI and waist circumference, as well as the need to consider psychological factors that might contribute to childhood obesity. With both clinical relevance and statistical significance, the findings from this study have the potential to contribute meaningfully to the development of clinical practice guidelines.

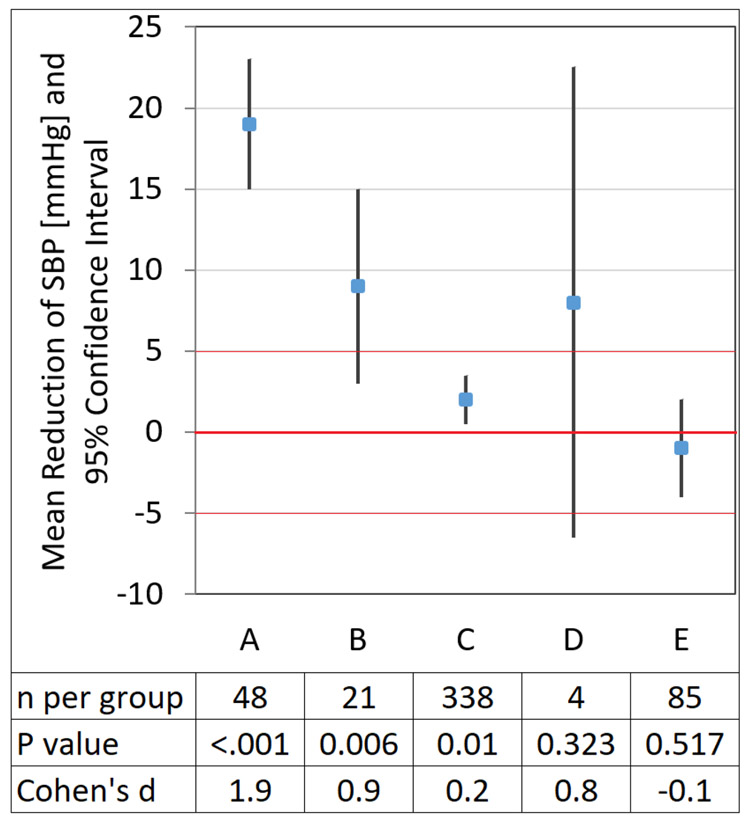
Graphical Comparison of Scenarios

In the discussion above, separate studies with different outcomes were used to illustrate the scenarios that can arise in the interplay between statistical significance and clinical relevance. Figure 1 includes a useful example for interpreting CIs in the context of a single predetermined clinically relevant outcome. This graphical example compares five hypothetical studies of interventions (vs. respective control groups) on SBP. A mean difference > 5 mm Hg (in either direction) is considered clinically relevant. In studies A–C, the 95% CI does not include 0, indicating a significant difference at a 0.05 significance level, whereas D and E correspond to a nonsignificant result. Studies A, B, and D indicate clinically relevant differences as the point estimate of intervention effect is > 5 mm Hg. However, due to the small sample size in D, the clinical benefit of intervention D beyond the sample is uncertain; the small sample data is compatible with a wide range of possible true intervention effects as indicated by the wide CI. Conversely, study C has a relatively large sample and is “statistically significant,” yet intervention C does not appear to provide a clinically relevant benefit, as both the point estimate of effect on SBP and the entire CI are within the predetermined region of no clinical relevance. The example shows how interpretation based on p-values and statistical significance is not necessarily congruent with interpretation based on clinical relevance, whereas interpretation based on observed effect and CI is informative (Schober et al., 2018).

Figure 1. Adapted with permission of P. Schober and Wolters Kluwer Health, Inc.

Results from five hypothetical trials (intervention vs. control) of different therapeutic approaches on elevated SBP. For the sake of the example, a mean change in SBP >5 mmHg was considered clinically relevant, and a standard deviation of 10 mmHg for SBP was assumed. Study A: the entire confidence interval (CI) is above the threshold of clinical relevance suggesting the observed reduction of SBP is not only statistically significant but also clinically relevant. Study B: the point estimate of mean SBP reduction is statistically significant and clinically relevant, however, the sample data are still compatible with clinically non relevant differences (the lower limit of the CI is < 5 mmHg), therefore clinical benefit beyond the sample is still uncertain. Study C: the point estimate of mean SBP reduction is statistically significant yet the intervention does not appear to provide a clinically relevant benefit as the entire CI is within the predetermined region of no clinical relevance. Study D: although the result is nonsignificant (the CI contains 0), the point estimate is above the clinical relevance threshold. Hence, the result is suggestive of benefit but inconclusive. It should not be interpreted as demonstrating no effect. Study E: the intervention does not appear beneficial as the point estimate indicates an increase in mean SBP (negative reduction in SBP) and the entire CI is within the predetermined region of no clinical relevance.

Conclusion

Researchers have a unique opportunity to shift the emphasis from simply evaluating statistical significance to reporting if research findings are clinically or practically relevant and whether results from a sample could apply to a larger population. This may be accomplished by examining effect sizes and CIs among variables of interest. Hypothesis-generating designs with smaller samples allows estimation of these effect sizes that can be used in subsequent research focused on hypothesis-testing. The definition of effect size is inclusive of difference in group means, correlation, proportion, and a variety of other measures. Reporting effect sizes and corresponding CIs will enhance the interpretation of research findings and improve synthesis of results across multiple studies. Editors are instrumental in publishing hypothesis-generating research and requiring the inclusion of effect sizes, CIs, and clinical relevance in all research reports.

With improvement in dissemination of clinical evidence, both the generator and consumer of clinical research become more engaged in integrating research evidence into practice. It is worth mentioning that there are freely accessible resources to calculate, interpret, and report effect sizes and CIs/credible intervals that are available. Table 3 includes several currently available resources that may be valuable to both novice and experienced researchers without the direct support of a statistician or medical librarian.

Table 3.

Resources to calculate, interpret, and report effect sizes and confidence/credible intervals

Resource	Location	Description
CI and other statistical calculation utilities with companion text	http://vassarstats.net/ http://vassarstats.net/textbook/	Calculates the CI of a correlation
Statistical calculator	https://www.danielsoper.com/statcalc/default.aspx	Calculates effect sizes and more for various analyses
Effect size magnitude guidelines resource	http://imaging.mrc-cbu.cam.ac.uk/statswiki/FAQ/effectSize	Guidelines for judging magnitude based on a variety of statistical tests
Statistical software for power analysis	https://www.psychologie.hhu.de/arbeitsgruppen/allgemeine-psychologie-und-arbeitspsychologie/gpower.html	Calculates power analysis and effect sizes and graphically displays results of power analyses
Bayesian framework and analysis	https://easystats.github.io/bayestestR/index.html	Includes an overview of Bayesian statistics with codes for analysis including credible intervals
PRISMA	http://www.prisma-statement.org	Recommendations for reporting systematic reviews and meta-analysis including CIs and measures of consistency
CONSORT	http://www.consort-statement.org/	Recommendations for reporting randomized trials including effect sizes and CIs
STROBE	https://www.strobe-statement.org/index.php?id=strobe-home	Recommendations surrounding the conduct and dissemination of observational studies in epidemiology; statement includes the aim of precision reporting with CIs