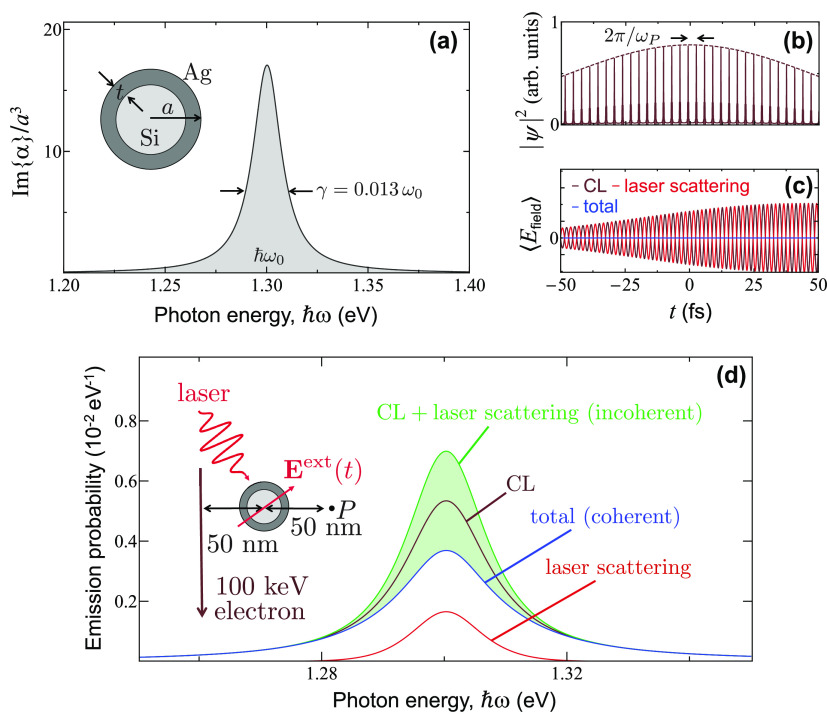
Figure 2.

Interference between cathodoluminescence and external light scattering. (a) We consider a sample consisting of a small isotropic scatterer described through a frequency-dependent polarizability α(ω) that is dominated by a single resonance of frequency ω₀ and width γ. For concreteness, we take a nanosphere (see inset) comprising a silicon core (60 nm diameter, ϵ = 12 permittivity) coated with a silver layer (5 nm thickness, permittivity taken from optical data⁷²), for which ℏω₀ = 1.3 eV and γ = 0.013ω₀. In the plot, the polarizability is normalized using the outer particle radius a = 35 nm. (b) Electron density profile of a 100 keV electron Gaussian wavepacket (50 fs standard deviation duration in probability density) after modulation through PINEM interaction (coupling coefficient |β| = 5, central laser frequency tuned to ω_P = ω₀) followed by free propagation over a distance d = 2.5 mm, which produces a train of temporally compressed density pulses. (c) Time dependence of the CL, laser scattering, and total field amplitudes for the electron in (b) and a laser Gaussian pulse of 50 fs duration in amplitude. The light amplitude is optimized to deplete the CL signal at frequency ω₀. (d) Spectral dependence of the resulting angle-integrated far-field CL (maroon curve), laser scattering (red curve), and total (blue curve) light intensity for the optimized amplitude of the Gaussian laser pulse. The incoherent sum of CL emission and laser scattering signals is shown for comparison (green curve). The shaded region corresponds to spectra obtained with partially optimized laser pulses. The inset in (d) shows details of the geometry under consideration, also indicating the position P at which the field in (c) is calculated.