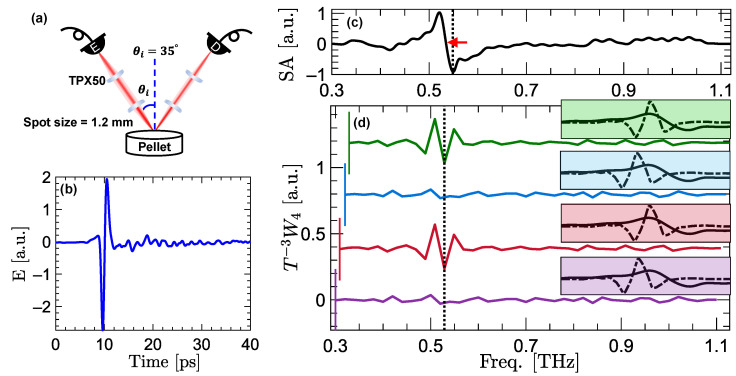
Figure 2.

(a) The schematic of the measurement setup. The specular reflections are measured at ${\theta }_i={\theta }_r={35}^{\circ }$. (b) An example THz pulse reflected from an $\alpha$-lactose pellet. (c) The spectral amplitude (SA) of $\alpha$-lactose over the frequency range of $f=0.3–1.13$ THz. A red arrow marks the zero-crossing at 0.53 THz, which is a characteristic resonance mode of $\alpha$-lactose. (d) The vertically-offset fourth-level DWT wavelet coefficients of SA, applied in the frequency domain. Each line in (d) is composed of the wavelet coefficients calculated from a different spectral range, i.e., $f=0.30–1.10$ THz in the purple trace, $f=0.31–1.11$ THz in the red trace, $f=0.32–1.12$ THz in the blue trace, and $f=0.33–1.13$ THz in the green trace. The lower bound of the frequency ranges are emphasized using vertical lines at the beginning of each trace. Each inset box shaded with the same color shows the overlap between the wavelet filter and the resonant signature at 0.53 THz in the corresponding reflection spectra. In each case, it can be noted that whether the resonance at 0.53 THz is resolved in $T^{-3}{W}_4$ depends on the overlap between the spectral feature and the DWT wavelet filter.