Abstract
Germination models are quite helpful in predicting emergence times, dormancy periods, and their applications in crop management. This study investigated the germination behaviors of Eruca sativa Mill. in response to fluctuations in temperatures (Ts) and water potentials (ψs). Germination percentage (GP) increased 95% with rising temperature within the range of 20–30 °C, and decreased 25% at 5 °C. Moreover, each ψ and T resulted in a decrease in GP as ψ decreased. Further, we noted that the θT1 value was substantially high at 30 °C and in (0 MPa), whereas the θT2 value was maximum at 10 °C (−0.02 MPa) and it decreased with decreasing Ψ. The maximum hydrothermal time constant (θHTT) and hydrotime (θH) values were obtained at 10 and 30 °C, respectively. In addition, a linear increase in the GR(g) pattern was observed at Tb and a decrease below the To. The calculated cardinal Ts was 5 °C for the base T, and 30 °C for both the optimum and ceiling T. The germination characteristics were higher at 30 °C having (0 MPa). Therefore, using cardinal temperatures, germination results, and the hydrothermal time model (HTT) could reveal the independent and interactive impacts of both T and the Ψ on the response of seed germination subjected to diverse environmental conditions.
Keywords: Eruca sativa, germination, cardinal temperature, hydrothermal constant, water stress
1. Introduction
The plant Eruca sativa Mill. (family: Brassicaceae) is a herbaceous industrial crop plant cultivated worldwide. It is primarily consumed fresh for its characteristic spicy flavor. Moreover, it is rich in health-promoting compounds with numerous medicinal properties [1]. The different extracts of this plant have been found to have anti-cancer, antioxidant, antithrombotic, and anti-inflammatory properties [2,3,4,5,6]. E. sativa contains a high level of erucic acid, making it a potential source of industrial oils [7]. The continuous change in climatic conditions has led to an increase in the frequency and intensity of abiotic stress factors that negatively impact plant growth, development, and yields [8,9,10,11].
The germination of seeds is a complex physiological phenomenon in the development of plants that is susceptible to abiotic factors including temperature, salinity, water potential, drought, and flooding [12,13,14,15]. Modeling seedling growth develops a quantitative description of how and why seeds germinate differently under various environmental conditions. For example, the effects of both temperature (T) and water potential (ψ), independently or interactively (T × ψ), impact germinating seeds studied with hydrotime, thermal time, and hydrothermal time models [16]. T and ψ are two key environmental stress factors that affect germination rate, germination percentage, and seedling emergence [17,18]. A hydrotime model estimates how seed germination is affected by water potential [19,20].
For instance, the germination process may be slowed or halted due to changes in the water potential of the permeation medium [21,22]. SG and sapling mortality are frequently caused by inadequate soil moisture, which initiates seed embryo metabolism and development [23]. The germination rate (GR) has a direct correlation with the variability between the surrounding ψ and the physiological threshold ψ for the emergence and growth of seedlings [16], and species distribution [24]. When there is no water limitation in the field, soil temperature also plays a significant role in seed germination and subsequent plant establishment [25]. When identifying the appropriate planting date for each crop, it is critical to know the three cardinal Ts of SG, namely Tb (low temperature; at which SG is equal to zero); To (optimum temperature; at which SG is maximum); and Tc (maximum or ceiling temperature; at which SG is equal to zero) [23,26,27]. Due to extreme temperature fluctuations and low atmospheric humidity and rainfall, water shortages are becoming a major concern for plant growth and productivity [28]. In order to optimally manage crop plants, including E. sativa, in changing climate conditions, it is important to gain a deeper understanding of several basic aspects, such as its geographical distribution, seed germination behavior, and seedlings’ metabolism and growth.
In terms of forecasting the behavior of seed germination and seedlings’ emergence to abiotic stress, the use of different models can be quite useful. For instance, the hydrotime (HT) and hydrothermal time models (HTT) are used to examine the response of seed germination to fluctuating ψ and T independently or interactively (ψ × T) [29]. The HTT model is a population-based threshold model that can characterize the concept of germination time to fluctuating ψ and T in the sub-optimal range (from Tb to To) and supra-optimal range (from To to Tc) [30]. Several plants, namely Sinapis arvensis L., Plantago ovata Forssk., Safflower, Papaver somniferum L., and Lathyrus spp., have adopted this approach so far [20,31,32].
This study aimed to investigate whether TT, HT, and HTT models can be used simultaneously to identify rocket seed germination responses to fluctuating ψ and T, independently or interactively (ψ × T). Evaluating seed behavior and seedling emergence will provide us with valuable insight into E. sativa productivity under continuously changing climatic conditions and/or its distribution around the world.
2. Materials and Methods
2.1. Seed Sowing and Stress Implementations
The rocket seeds (Eruca sativa Mill.) were generously contributed by the Pakistan Forest Institute (PFI), Khyber Pakhtunkhwa (KP) Pakistan. After being treated with 95% ethanol (3 min), the seeds were washed with double distilled water and dried at a normal temperature under shade conditions. A Petri dish experiment was performed following the randomized complete block design (RCBD), at the Department of Botany, University of Peshawar, KP, Pakistan, by subjecting seeds to fluctuating Ψs (0, −0.01, −0.02, and −0.05 MPa) [33] and T (5, 10, 15, 20 and 30 °C). There were 40 seeds per Petri dish on the Wathman No. 1 filter paper, dampened with double distilled water (5 mL) and PEG6000 solutions. Each treatment was repeated three times, and the Petri dishes’ data were taken daily for four consecutive days in a week. The experiment was repeated weekly, changing the incubation temperature. Radicles were measured daily. When seeds reached a length of one millimeter, they were considered to have germinated. At the end of the experiment, (96 h), the germinated seeds were pulled out and measured for several germination characteristics. The germination characteristics for the TT, HT, and HTT models were established following a repeated probit regression analysis [12,16,26,34]. The sub- and supra-optimal Ts were obtained from the following equation based on the HTT concept.
2.2. Data Analysis
The germination data were evaluated using the concept of TT, HT, and HTT models [35,36], through a repeated probit regression analysis. The germination rate (GR) for each percentile at each T or Ψ was calculated as the inverse of the germination time.
2.3. Thermal Time (TT)
We quantified the germination time data of constant Ts at each Ψ using the concept of TT.
| (1) |
| (2) |
Thus, the germination rate is inversely related to the time of seed emergence, and Equations (1) and (2) may be represented as Equation (3):
| (3) |
where θT1, θT2, T, and Tb(g) stand for the thermal time constants (°C h), expected temperature for seed germination, base temperature for germination fraction, and the time to germination fraction, respectively.
2.4. Hydrotime (HT)
The HT model was used to analyze the SG response to Ψs and accelerated aging [29]. Likewise, as in the TT model, θH calculates the relation between the germination rate and solute potential. The HT model may be exhibited as follows:
| (4) |
| (5) |
where θH, Ψ, Ψb(g), tg, and GR(g) stand for the hydrotime constant (MPa h), actual water potential, the base water potential of germination fraction g (%), the time of seed population for the emergence of radicle, and the actual time to germination fraction g, respectively.
2.5. Hydrothermal Time Model (HTT)
We can merge the TT and HT models into a hybrid HTT model for predicting and describing SG behaviors to different Ψ and T. According to the HTT model, the germination time course at all Ts and Ψ (from Tb to To) can be calculated as follows:
| (6) |
| (7) |
where θHTT, To, and kT stand for the HTT constant (MPa h), the optimum temperature for germination fraction, and the Boltzmann constant, respectively.
2.6. Germination Parameters
Based on the germination rate, root length, shoot lengths, leaf lengths, and the fresh and dry weights of plants, the following germination indices have been calculated.
2.6.1. Germination Energy (GE)
The GE of plants was calculated following standard procedure [37].
| (8) |
Here X1, X2 and Xn represent the frequency of germinated seeds on the first day, second day, and so on. Additionally, Y1, Y2 and Yn are the number of days from sowing to the first, second, and up to the last day’s count.
2.6.2. Mean Germination Time (MGT)
The MGT index, which measures the speed with which seeds are emerging within a population, was calculated according to the following equation [38]:
| (9) |
where f represents seeds that germinated on day X.
2.6.3. Mean Germination Rate (MGR)
The following formula was used to determine the MGR [39]:
| (10) |
2.6.4. Coefficient of Variation of Germination Time (CVt)
The value of CVt was calculated according to the following equation [40]:
| (11) |
where St and t stand for the standard deviation of the germination time and mean germination time, respectively.
2.6.5. Coefficient of Velocity of Germination (CVG)
The CVG represents the rate at which seeds germinate, and it will enhance with an increase in the frequency of germinating seeds. All sown seeds should germinate within the first 24 h to achieve the highest theoretical CVG. The following formula was used to calculate the CVG values [37]:
| (12) |
In this example, N stands for the number of seeds that germinate each day, and T stands for the time between sowing and germination of the N number of seeds.
2.6.6. Germination Index (GI)
The value of the GI indicates the rate and speed of seed germination and was calculated using the following equation [41]:
| (13) |
where n1, n2, …, n10 illustrate the frequency of seed germination on the first, second, and last days of the experimental trial.
2.6.7. Germination Rate Index (GRI)
The value of the GRI that describes the percentage of germination on certain days and at certain times was calculated according to the following equation [42]:
| (14) |
where G1 and G2 represent the PG on the first and second day after sowing, respectively, and Gx represents the final GP.
2.6.8. Seed Vigor Index-1 (SVI-1)
From each pot, the length of three seedlings was measured (cm) and calculated according to the following method [43]:
| (15) |
2.6.9. Seed Vigor Index-2 (SVI-2)
Dry weight was calculated for three seedlings from each pot using an electrical balance. The values were then put into an equation and multiplied by the GP, using the following equation [44]:
| (16) |
2.6.10. Time to 50% Germination (T50%)
The value of T50% that illustrates the time needed for 50% of a seed to germinate was quantified by the following equation [45]:
| (17) |
where N represents the number of emerged seeds, and nj and ni represent the number of seeds that emerged after adjacent counts between tj and ti, where ni* N/2 > Nj.
2.6.11. Root-Shoot Ratio (RSR)
We calculated the RSR using the following equation after the roots and shoots were dried in the oven for 24 h [43]:
| (18) |
2.6.12. Germination Percentage (GP)
The GP illustrates the number of seeds germinated per 100 seeds sown in each pot, calculated using the following equation [38]:
| (19) |
2.7. Statistical Analysis
We conducted a linear regression built with IBM® SPSS® Statistics Software Version 26.0 and SigmaPlot 11.0 to examine the effects of T (thermal model), ψ (hydrotime model), and their combined effects, i.e., T × ψ (hydrothermal time model). The basic statistical calculations were performed using Microsoft Excel. The values of σΨb; Ψb(50), R2, SE, F, t-test, and Sig were calculated following a linear probit regression analysis in SPSS. Moreover, OriginPro® 2021 Software (OriginLab Corporation, Northampton, MA, USA) was used to plot graphs of germination fractions against rapid aging duration, and germination characteristics against T.
3. Results
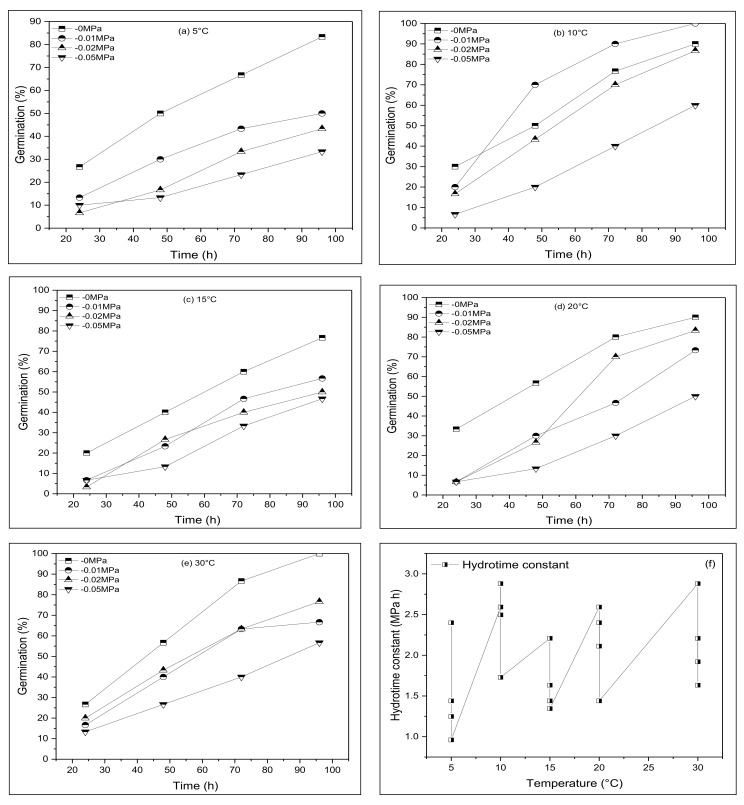
The final germination percentage (GP) of the rocket was greatly influenced by the fluctuating water potential (ψ) and temperature (T), as well their interactions (ψ × T) (p ≤ 0.05). The germination rate (GR) increased by 95% upon the rising temperature within the range of 20–30 °C. In contrast, the GR was recorded at 5 and 20 °C (~10 °C). In general, the GR appeared more responsive to changes in ψ than T. The highest GP was displayed at 30 °C in (0 MPa) and the minimum was at 5 and 20 °C. At each ψ and T, the germination percentage decreased as ψ decreased (Figure 1a–e). Throughout the experiment, the highest daily GP was reported on the last day under the distilling water (0 MPa). At ψ equal to (−0.02 MPa), zero growth was shown at the Ts of 5, 10, 15, and 30 °C and seed germination (SG) was <20% at 5, 15, and 20 °C. The results confirmed that the value of θT1 was substantially high at 30 °C in (0 MPa) and at a minimum at 5 °C in ψ (−0.05 MPa) (Table 1). The value of θT2 was at a maximum at 10 °C (−0.02 MPa). The maximum values of θH and θHTT were noticed at 10 and 30 °C, respectively. Moreover, the HTT model illustrated that the impact of ψ on seed germination was moderately high in comparison to T. Water potentials and seed population germination fractions were plotted against a constant T in the data set of θH (Figure 1f). When the GR was exhibited against contrasting T percentiles, a linear rise in the GR(g) pattern was observed at an optimum temperature (Tb) and a decrease below the base temperature (To). The GR(g) of the HT model exhibited an increase at 5 °C in (−0.05 MPa).
Figure 1.
A cumulative germination fraction for Eruca sativa Mill. at (a) 5 °C, (b) 10 °C, (c) 15 °C, (d) 20 °C, (e) 30 °C, having different water potentials, (f) changes in halotime constant (θH) as a function of temperature (T) for Eruca sativa Mill. symbols indicate water potential and lines indicate cumulative germination.
Table 1.
The estimated parameters of the hydro and thermal time models to describe Eruca sativa Mill. seed germination under fluctuating different temperatures (Ts) and water potentials (ψs).
| T (°C) |
ψ (MPa) |
TTsub (θT1) | TTsupra (θT2) |
θH (MPa h) |
θHTT (MPa h) |
Hydro Time GR(g) | Thermal Time GR(g) |
|---|---|---|---|---|---|---|---|
| 5 °C | 0 | 1600 | 2000 | 2.4 | 48 | 0.013 | 0.01 |
| −0.01 | 960 | 1200 | 1.44 | 28.8 | 0.021 | 0.02 | |
| −0.02 | 832 | 1040 | 1.248 | 24.96 | 0.024 | 0.02 | |
| −0.05 | 640 | 800 | 0.96 | 19.2 | 0.031 | 0.03 | |
| 10 °C | 0 | 1728 | 2160 | 2.592 | 51.84 | 0.012 | 0.01 |
| −0.01 | 1920 | 2400 | 2.88 | 57.6 | 0.010 | 0.01 | |
| −0.02 | 1664 | 2080 | 2.496 | 49.92 | 0.012 | 0.01 | |
| −0.05 | 1152 | 1440 | 1.728 | 34.56 | 0.017 | 0.02 | |
| 15 °C | 0 | 1472 | 1840 | 2.208 | 44.16 | 0.014 | 0.01 |
| −0.01 | 1088 | 1360 | 1.632 | 32.64 | 0.018 | 0.02 | |
| −0.02 | 960 | 1200 | 1.44 | 28.8 | 0.021 | 0.02 | |
| −0.05 | 896 | 1120 | 1.344 | 26.88 | 0.022 | 0.02 | |
| 20 °C | 0 | 1728 | 2160 | 2.592 | 51.84 | 0.012 | 0.01 |
| −0.01 | 1408 | 1760 | 2.112 | 42.24 | 0.014 | 0.01 | |
| −0.02 | 1600 | 2000 | 2.4 | 48 | 0.013 | 0.01 | |
| −0.05 | 960 | 1200 | 1.44 | 28.8 | 0.021 | 0.02 | |
| 30 °C | 0 | 1920 | 2400 | 2.88 | 57.6 | 0.010 | 0.01 |
| −0.01 | 1280 | 1600 | 1.92 | 38.4 | 0.016 | 0.02 | |
| −0.02 | 1472 | 1840 | 2.208 | 44.16 | 0.014 | 0.01 | |
| −0.05 | 1088 | 1360 | 1.632 | 32.64 | 0.018 | 0.02 |
T (Temperatures); ψ (Water potential); TTsub (Thermal time constant at sub-optimal temperature); TTsupra (Thermal time constant at supra-optimal temperature); θH (Hydrotime constant); θHTT (Hydrothermal time constant); GR (Germination rate).
The TT model well represented the kinetic of germination for the ψ range (0 to −0.05 MPa) and rising T at sub-optimal and supra-optimal. Moreover, the TT model was clinging to germination fraction data under distilled water with an increasing R2 value (0.829). Furthermore, GR(g) responses were applied to calculate the ceiling, optimum, and base temperatures (Table 2). The consistency in σψb showed that this change was maintained across all T and ψ level combinations, and similarly the least base water potential at 50% germination value (−0.18) was observed at 30 °C. The F value also showed an asymmetrical etiquette pattern, having no linear pattern, except that which was calculated to be high at 20 °C (Table 2). Our study showed that the minimum temperature observed (Tb) for E. sativa was 5°C; below this threshold, the germination rate dropped and the plant’s physiological processes became harder to sustain. Optimal temperatures (To) and ceiling temperatures (Tc) were determined to be 30 °C (Table 3).
Table 2.
Estimation of hydrotime model parameters for Eruca sativa using non-linear regression.
| Temperature | ψb(50) (MPa) | σψb (MPa) | R2 | R | SE | F | Sig. |
|---|---|---|---|---|---|---|---|
| 5 °C | −0.13 | 0.142 | 0.695 | 0.834 | 1.464 | 4.559 | 0.16 |
| 10 °C | −0.15 | 0.153 | 0.815 | 0.903 | 0.901 | 8.793 | 0.09 |
| 15 °C | −0.19 | 0.176 | 0.640 | 0.800 | 0.991 | 3.558 | 0.20 |
| 20 °C | −0.11 | 0.187 | 0.829 | 0.911 | 0.883 | 9.702 | 0.08 |
| 30 °C | −0.21 | 0.133 | 0.647 | 0.805 | 1.338 | 3.673 | 0.19 |
ψb(50) (Base water potential at 50 percentile); σψb (Standard deviation in Ψb); R2 (Coefficient of determination); SE (Standard error); F (Variability between different means); Sig (Level of significance).
Table 3.
Estimated germination and cardinal temperature values for Eruca sativa Mill. using the hydrothermal time model.
| Variables | Eruca sativa Mill. |
|---|---|
| Hydrothermal time model parameters | |
| Ѱb (50) (MPa) | −0.18 |
| σψb (MPa) | −0.13 |
| θHTT (MPa °C h−1) | 43.2 |
| kT (MPa °C h−1) | 0.104 |
| Cardinal temperatures | |
| Tb (°C) | 5 |
| To (°C) | 30 |
| Tc (°C) | 30 |
| R2 | 0.829 |
kT (Boltzmann constant); R2 (Coefficient of determination).
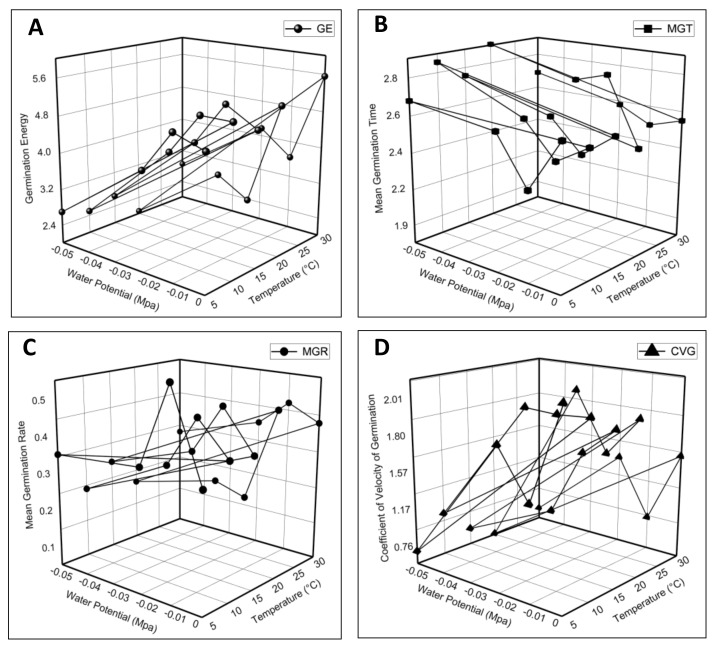
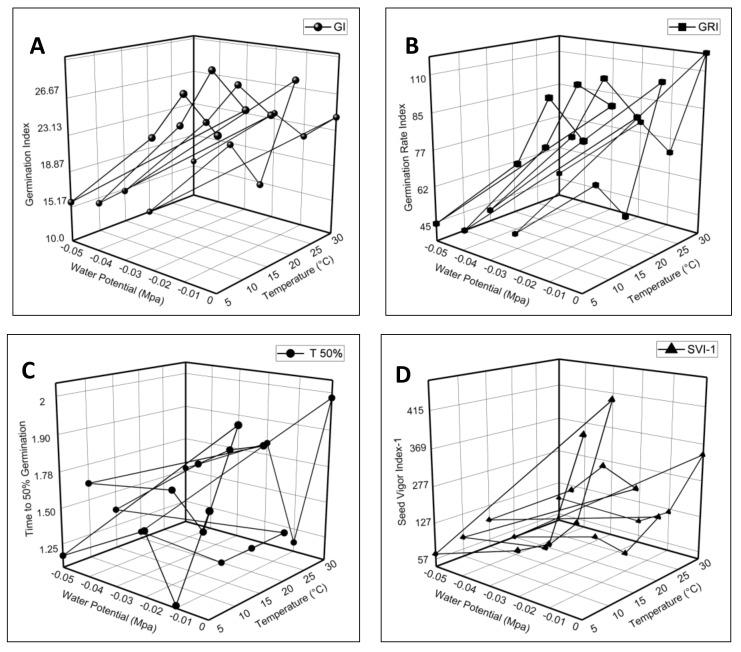
The current HTT model experiment demonstrated that fluctuating ψ and T had a significant impact on E. sativa germination characteristics. The data of the germination parameters plotted against ψ and T were presented in 3D graphs. The results of the Petri dish experiment showed that the highest GE and GP were observed in seeds subjected to 30 °C (0 MPa), and a minimum at 20 °C in (−0.05 MPa) (Figure 2A). A maximum MGT was observed at 20 °C in (−0.01 MPa), and the minimum value was observed at 5 °C in −0.01 MPa (Figure 2B). Furthermore, the highest MGR reported in seeds was subjected to 5 °C in (−0.01 MPa), and the lowest at 10 °C in (−0.05 MPa) as shown in Figure 2C. The value of the CVG was at a maximum at 5 °C in distilled water, and a minimum at 20 °C in (−0.05 MPa) (Figure 2D). Moreover, the results also revealed the maximum GI value reported at 10 °C in (−0.01 MPa), and the lowest at 20 °C in (−0.05 MPa) as shown in Figure 3A.
Figure 2.
The effect of the water potential and temperature on (A) germination energy; (B) mean germination time; (C) mean germination rate; and (D) coefficient of the velocity of germination of Eruca sativa Mill.
Figure 3.
The effect of water potential and temperature on (A) germination index; (B) germination rate index; (C) time to 50% germination; and (D) seed vigor index-I of germination of Eruca sativa Mill.
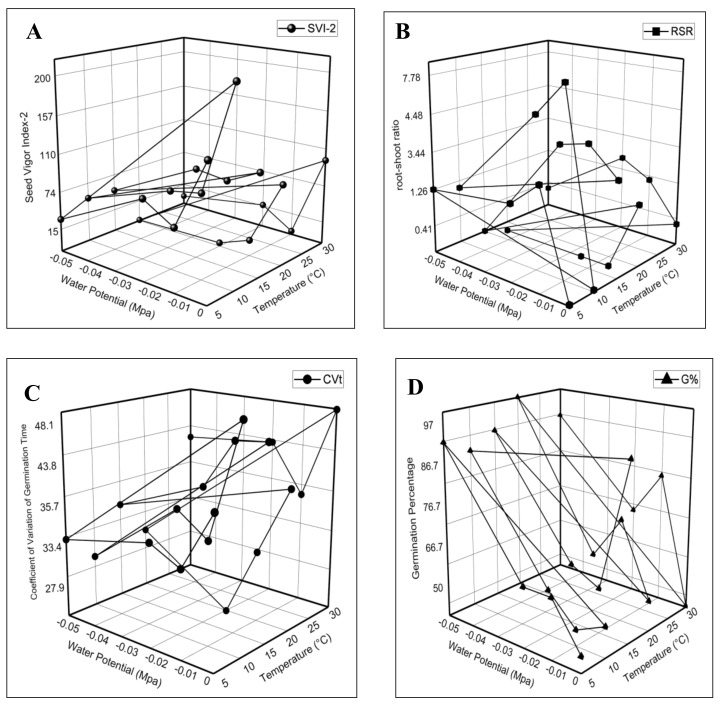
The maximum value of the germination rate index (GRI) was in seeds at 30 °C in (0 MPa) and the minimum value was at 10 °C in (−0.05 MPa) (Figure 3B). The results revealed the higher T50% and coefficient of variation of the germination time (CVt) value in seeds treated with 30 °C in (0 MPa), and a minimum recorded at 20 °C in (−0.02 MPa) (Figure 3C and Figure 4C). Seed vigor indexes 1 and 2 recorded the maximum value at 10 °C in (0 MPa) and the minimum at 20 °C in (−0.05 MPa) (Figure 3D and Figure 4A). In addition, the highest root-shoot ratio (RSR) recorded was in seeds subjected to 10 °C in (−0.01 MPa), and the lowest was at 15 °C in (−0.05 MPa) (Figure 4B). Our findings illustrate that the germination characteristics were decreased when the water potential declined at each temperature, and these were at a maximum at the optimum temperature.
Figure 4.
The effect of water potential and temperature on (A) seed vigor index-2; (B) root-shoot ratio; (C) coefficient of variation of germination time; and (D) germination percentage of germination of Eruca sativa Mill.
4. Discussion
Identifying the optimal geographical area, where a species can germinate and thrive, requires examining germination patterns under various environmental conditions. In this respect, mathematical models (TT, HT, and HTT models) are effective in quantifying the influence of these stress factors on seed germination [30]. Temperature (T) is one of the key environmental factors that impact seed germination in numerous plant species [46,47,48]. In addition, water stress is another abiotic stress factor that restricts early seedling and seed germination [49].
Several studies developed hydrotime (HT), thermal time (TT), and hydrothermal time (HTT) models as effective methods to describe and predict seed population germination responses under different environmental factors [20,34,50,51,52]. These models are common tools for both agronomical and basic research because they are simple and provide a direct biological interpretation of the parameters.
In the present study, we evaluated the response of E. sativa seeds to fluctuating Ψ and T using a hydrothermal model, by exploiting its flexibility for providing physiological cues that may be utilized in the future management of this crop species. The results of our study showed that increasing temperatures within the range of 20–30 °C resulted in an increase of 95% in germination, and the lowest value displayed a 25% decrease at 5 and 20 °C (~10 °C). The maximum growth rate was found at 30 °C, and the minimum was found at 5 °C. These findings are consistent with several previous studies [23,26,34,48,53,54]. According to them, agronomic parameters are affected significantly by T and Ψ, and when the Ψ becomes more negative, both the rate and percentage of germination decrease (if they do not become completely inhibited) due to the water deficit [55,56]. An explanation for the decrease in GP could be the thermal denaturation of essential amino acids that play a significant role in seed germination [57]. The declining pattern of GP coincides with a reduction in Ψ, which can lead to a decrease in water potential and a corresponding reduction in water resources [58,59].
In our study, the minimum temperature (Tb) observed for E. sativa was 5 °C. It is an essential cardinal temperature threshold below which the germination rate drops and the physiological processes of a plant are more difficult to sustain; thus, Tb must be considered in the development of a crop simulation model and determination of the optimum growing period [60]. In general, seeds are incubated at a constant T under laboratory conditions; however, they may face the problem of T fluctuations at the seedlings’ emergence stage in the field conditions. Seeds exposed to a changing temperature accumulated fewer thermal hours than those exposed to a constant temperature [61]. During the present study, the optimum (To) and ceiling (Tc) temperatures were both recorded at 30 °C. There are approximately three cardinal temperatures, including the ceiling (Tc) and base (Tb) temperatures, at which germination rates are minimal; and the optimal temperature (To) at which high germination occurs immediately [62].
Further, the To (30 °C) observed in the current study is comparable to the To ranges between 25 and 28 °C (30 °C) observed in previous studies for watermelons [63,64,65]. Further, the maximum hydrotime constant (θH) value was recorded at 10 °C. The GR(g) of the HT concept exhibited a considerable increase at 5 °C in (−0.05 MPa). Despite θH and GR(g) being in contradiction with observations reported for Sesamum indicum [34] and potatoes [66], the decrease in water potential was associated with an increase in GR(g) values, which are in agreement with the previous results for Melissa officinalis [67] and Citrullus lanatus [30]. Researchers and breeders used the θH values to grade cultivars based on their susceptibility to ψ. In addition, the consistency in σψb showed that this alteration was sustained at all combinations of T and ψ values, and likewise, the lowest base water potential at 50% germination value (−0.18) was recorded at 30 °C. The ψb(g) is an indicator that represents uniform changes in seed germination within a seed lot [24]. The results of several studies suggest that ψb(g) values are minimal at To and increase linearly (e.g., become more positive) at supra-optimal Ts, as reported for the tomato [68], potato [66], carrot and onion [51], zucchini [69], and watermelon [30].
TT and HT concepts have been effectively applied to explain SG attributes at T (sub-and supra-optimal) and ψ. However, the TT concept demonstrated an error at sub-optimal Ts by failing to predict the decrease in GR when Ts > To. Therefore, to overcome this problem, Bradford developed the HTT model [67]. Currently, the HTT concept can be used to examine how abiotic factors (T and ψ) interactively influence the SG in seed lots [69,70]. In the present study, the maximum θHTT value was recorded at 30 °C. The HTT model investigated for Polylepis besseri had predicted that the values of Tb, To, and Tc were 3.08, 21.78, and 27.9 °C, respectively [71]. Based on the HTT model, the comparison results indicated that seed germination is more affected by water potential than by temperature.
The results showed that germination parameters like GE, CVt, GP, GRI, and T50% were observed to be high in seeds grown at 30 °C and having zero water potential. The germination characteristics decreased when the water potential declined at each temperature, and these were at a maximum at the optimum temperature. Low Ψ can inhibit the chemical reactions and physiological mechanisms in the seed [69,72]. There is a particular significance of water stress in crop management because these factors represent the component of greatest trouble for both farmers and customers [73,74]. Therefore, using cardinal temperatures, germination results, and the hydrothermal time model (HTT) could reveal the response of seed germination to fluctuating ψ and T, independently or interactively (ψ × T).
5. Conclusions
The maximum GP was observed at 30 °C (0 MPa), and the minimum at 5 and 20 °C. The cardinal Ts followed the pattern of 30 °C for Tc, 30 °C for To, and 5 °C for Tb. Moreover, the θH and θHTT values were measured at 10 and 30 °C, respectively. Using the TT and HT models, the maximum θT1 and θT2 values were recorded in (0 and −0.02 MPa) at 30 and 10 °C; Ψb(50) in (−0.18 MPa); and the σΨb value in (−0.13 MPa) at kT (0.104 MPa) °C h−1. The germination parameters like GE, CVt, GP, GRI, and T50% were observed to be high in seeds grown at 30 °C having zero water potential. As a result of reducing the water potential at all temperatures, germination was either retarded or inhibited. Therefore, using cardinal temperatures, germination results, and the hydrothermal time model (HTT) could reveal the response of seed germination to fluctuating ψ and T, independently or interactively (ψ × T), in the face of future climatic changes. However, the parameters of the model should analyze the physiological response of rocket seed populations under the influence of different abiotic factors for predicting the future germination time courses.
Acknowledgments
The Researchers Supporting Project number (RSP-2021/219) King Saud University, Riyadh, Saudi Arabia, is gratefully acknowledged. We are also thankful to the Department of Botany, University of Peshawar, for providing all facilities of this work.
Author Contributions
Conceptualization, S.U. and S.A.; methodology, S.U., S.K. and A.U.; software, S.K., A.U. and S.U.; validation, S.K., A.U., S.U. and S.A.; formal analysis, S.K., A.U., S.U., Y.C. and M.H.S.; investigation, S.K., A.U., S.U. and M.H.S.; resources, S.U. and S.A.; data curation, S.K., A.U. and S.U.; writing—original draft preparation, S.K., A.U. and S.U.; writing—review and editing, S.U., M.K.O., A.A.-H., Y.C. and S.A.; visualization, S.U., S.A., A.U., M.H.S. and Y.C.; supervision, S.U. and S.A.; project administration, S.U. and S.A.; funding acquisition, M.K.O. and A.A.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This study received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Bhandari S.R., Jo J.S., Lee J.G. Comparison of Glucosinolate Profiles in Different Tissues of Nine Brassica Crops. Molecules. 2015;20:15827–15841. doi: 10.3390/molecules200915827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Alam M.S., Kaur G., Jabbar Z., Javed K., Athar M. Eruca sativa seeds possess antioxidant activity and exert a protective effect on mercuric chloride induced renal toxicity. Food Chem. Toxicol. 2007;45:910–920. doi: 10.1016/j.fct.2006.11.013. [DOI] [PubMed] [Google Scholar]
- 3.Khoobchandani M., Ganesh N., Gabbanini S., Valgimigli L., Srivastava M. Phytochemical potential of Eruca sativa for inhibition of melanoma tumor growth. Fitoterapia. 2011;82:647–653. doi: 10.1016/j.fitote.2011.02.004. [DOI] [PubMed] [Google Scholar]
- 4.Fuentes E., Alarcón M., Fuentes M., Carrasco G., Palomo I. A novel role of Eruca sativa Mill. (rocket) extract: Antiplatelet (NF-κB inhibition) and antithrombotic activities. Nutrients. 2014;6:5839–5852. doi: 10.3390/nu6125839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gugliandolo A., Giacoppo S., Ficicchia M., Aliquï A., Bramanti P., Mazzon E. Eruca sativa seed extract: A novel natural product able to counteract neuroinflammation. Mol. Med. Rep. 2018;17:6235–6244. doi: 10.3892/mmr.2018.8695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Walayat N., Wang X., Nawaz A., Zhang Z., Abdullah A., Khalifa I., Saleem M.H., Mushtaq B.S., Pateiro M., Lorenzo J.M., et al. Ovalbumin and Kappa-Carrageenan Mixture Suppresses the Oxidative and Structural Changes in the Myofibrillar Proteins of Grass Carp (Ctenopharyngodon idella) during Frozen Storage. Antioxidants. 2021;10:1186. doi: 10.3390/antiox10081186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pignone D., Gomez-Campo C. Eruca. In: Kole C., editor. Wild Crop Relatives: Genomic and Breeding Resources, Oilseeds. Springer; Berlin/Heidelberg, Germany: 2011. [Google Scholar]
- 8.Saleem M.H., Fahad S., Khan S.U., Din M., Ullah A., El Sabagh A., Hossain A., Llanes A., Liu L. Copper-induced oxidative stress, initiation of antioxidants and phytoremediation potential of flax (Linum usitatissimum L.) seedlings grown under the mixing of two different soils of China. Environ. Sci. Pollut. Res. 2019;27:5211–5221. doi: 10.1007/s11356-019-07264-7. [DOI] [PubMed] [Google Scholar]
- 9.Saleem M.H., Ali S., Rehman M., Rana M.S., Rizwan M., Kamran M., Imran M., Riaz M., Soliman M.H., Elkelish A., et al. Influence of phosphorus on copper phytoextraction via modulating cellular organelles in two jute (Corchorus capsularis L.) varieties grown in a copper mining soil of Hubei Province, China. Chemosphere. 2020;248:126032. doi: 10.1016/j.chemosphere.2020.126032. [DOI] [PubMed] [Google Scholar]
- 10.Ali B., Wang X., Saleem M.H., Hafeez A., Afridi M.S., Khan S., Ullah I., Amaral Júnior A.T.D., Alatawi A., Ali S. PGPR-Mediated Salt Tolerance in Maize by Modulating Plant Physiology, Antioxidant Defense, Compatible Solutes Accumulation and Bio-Surfactant Producing Genes. Plants. 2022;11:345. doi: 10.3390/plants11030345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zaheer I.E., Ali S., Saleem M.H., Yousaf H.S., Malik A., Abbas Z., Rizwan M., Abualreesh M.H., Alatawi A., Wang X. Combined application of zinc and iron-lysine and its effects on morpho-physiological traits, antioxidant capacity and chromium uptake in rapeseed (Brassica napus L.) PLoS ONE. 2022;17:e0262140. doi: 10.1371/journal.pone.0262140. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 12.Bakhshandeh E., Gholamhossieni M. Quantification of soybean seed germination response to seed deterioration under PEG-induced water stress using hydrotime concept. Acta Physiol. Plant. 2018;40:126. doi: 10.1007/s11738-018-2700-1. [DOI] [Google Scholar]
- 13.Shah S., Khan S., Sulaiman S., Muhammad M., Badsha L., Bussmann R.W., Hussain W. Quantitative study on medicinal plants traded in selected herbal markets of Khyber Pakhtunkhwa, Pakistan. Ethnobot. Res. Appl. 2020;20:1–36. doi: 10.32859/era.20.57.1-36. [DOI] [Google Scholar]
- 14.Luo X., Dai Y., Zheng C., Yang Y., Chen W., Wang Q., Chandrasekaran U., Du J., Liu W., Shu K. The ABI4-RbohD/VTC2 regulatory module promotes reactive oxygen species (ROS) accumulation to decrease seed germination under salinity stress. New Phytol. 2021;229:950–962. doi: 10.1111/nph.16921. [DOI] [PubMed] [Google Scholar]
- 15.Ullah A., Sadaf S., Ullah S., Alshaya H., Okla M.K., Alwasel Y.A., Tariq A. Using Halothermal Time Model to Describe Barley (Hordeumvulgare L.) Seed Germination Response to Water Potential and Temperature. Life. 2022;12:209. doi: 10.3390/life12020209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Saberali S., Shirmohamadi-Aliakbarkhani Z. Quantifying seed germination response of melon (Cucumis melo L.) to temperature and water potential: Thermal time, hydrotime and hydrothermal time models. S. Afr. J. Bot. 2020;130:240–249. doi: 10.1016/j.sajb.2019.12.024. [DOI] [Google Scholar]
- 17.Esmaeil B., Hemmatollah P., Fatemeh V., Mobina G. Quantification of the effect of environmental factors on seed germination and seedling growth of Eruca (Eruca sativa) using mathematical models. J. Plant Growth Regul. 2020;39:190–204. [Google Scholar]
- 18.Shah S., Ullah S., Ali S., Khan A., Ali M., Hassan S. Using mathematical models to evaluate germination rate and seedlings length of chickpea seed (Cicer arietinum L.) to osmotic stress at cardinal temperatures. PLoS ONE. 2021;16:e0260990. doi: 10.1371/journal.pone.0260990. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 19.Soltani E., Soltani A., Oveisi M. Modeling seed aging effect on wheat seedling emergence in drought stress: Optimizing germin program to predict emergence pattern. J. Crops Improv. 2013;15:147–160. [Google Scholar]
- 20.Bidgoly R.O., Balouchi H., Soltani E., Moradi A. Effect of temperature and water potential on Carthamus tinctorius L. seed germination: Quantification of the cardinal temperatures and modeling using hydrothermal time. Ind. Crop. Prod. 2018;113:121–127. doi: 10.1016/j.indcrop.2018.01.017. [DOI] [Google Scholar]
- 21.Mahmood A., Awan M.I., Sadaf S., Mukhtar A., Wang X., Fiaz S., Khan S.A., Ali H., Muhammad F., Hayat Z., et al. Bio-diesel production of sunflower through sulphur management in a semi-arid subtropical environment. Environ. Sci. Pollut. Res. 2021;29:13268–13278. doi: 10.1007/s11356-021-16688-z. [DOI] [PubMed] [Google Scholar]
- 22.Saleem M.H., Ali S., Seleiman M.F., Rizwan M., Rehman M., Akram N.A., Liu L., Alotaibi M., Al-Ashkar I., Mubushar M. Assessing the Correlations between Different Traits in Copper-Sensitive and Copper-Resistant Varieties of Jute (Corchorus capsularis L.) Plants. 2019;8:545. doi: 10.3390/plants8120545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bewley J.D., Black M. Seeds: Physiology of Development and Germination. Springer Science & Business Media; Berlin/Heidelberg, Germany: 2013. [Google Scholar]
- 24.Abdellaoui R., Boughalleb F., Zayoud D., Neffati M., Bakhshandeh E. Quantification of Retama raetam seed germination response to temperature and water potential using hydrothermal time concept. Environ. Exp. Bot. 2019;157:211–216. doi: 10.1016/j.envexpbot.2018.10.014. [DOI] [Google Scholar]
- 25.Patanè C., Saita A., Tubeileh A., Cosentino S.L., Cavallaro V. Modeling seed germination of unprimed and primed seeds of sweet sorghum under PEG-induced water stress through the hydrotime analysis. Acta Physiol. Plant. 2016;38:115. doi: 10.1007/s11738-016-2135-5. [DOI] [Google Scholar]
- 26.Bakhshandeh E., Atashi S., Hafez-Nia M., Pirdashti H. Quantification of the response of germination rate to temperature in sesame (Sesamum indicum) Seed Sci. Technol. 2013;41:469–473. doi: 10.15258/sst.2013.41.3.14. [DOI] [Google Scholar]
- 27.Parmoon G., Moosavi S.A., Siadat S.A. How salinity stress influences the thermal time requirements of seed germination in Silybum marianum and Calendula officinalis. Acta Physiol. Plant. 2018;40:175. doi: 10.1007/s11738-018-2750-4. [DOI] [Google Scholar]
- 28.Fakhfakh L.M., Anjum N.A., Chaieb M. Effects of temperature and water limitation on the germination of Stipagrostis ciliata seeds collected from Sidi Bouzid Governorate in Central Tunisia. J. Arid Land. 2018;10:304–315. doi: 10.1007/s40333-018-0050-x. [DOI] [Google Scholar]
- 29.Gummerson R.J. The Effect of Constant Temperatures and Osmotic Potentials on the Germination of Sugar Beet. J. Exp. Bot. 1986;37:729–741. doi: 10.1093/jxb/37.6.729. [DOI] [Google Scholar]
- 30.Bakhshandeh E., Atashi S., Hafeznia M., Pirdashti H., Da Silva J.A.T. Hydrothermal time analysis of watermelon (Citrullus vulgaris cv. ‘Crimson sweet’) seed germination. Acta Physiol. Plant. 2014;37:1738. doi: 10.1007/s11738-014-1738-y. [DOI] [Google Scholar]
- 31.Tabrizi L., Nasiri M.M., Kouchaki A.R. Investigations on the cardinal temperatures for germination of plantago ovata and plantago psyllium. Iran. J. Field Crops Res. 2005;2:143–150. [Google Scholar]
- 32.Alahmadi J.M., Tomaj A.N., Zangui M. Determination of cardinal temperatures of seed germination (Lathyrus sativus max L.) J. Seed Ecophysiol. 2015;1:43–56. [Google Scholar]
- 33.Michel B.E., Kaufmann M.R. The Osmotic Potential of Polyethylene Glycol. Plant Physiol. 1973;51:914–916. doi: 10.1104/pp.51.5.914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bakhshandeh E., Jamali M., Afshoon E., Gholamhossieni M. Using hydrothermal time concept to describe sesame (Sesamum indicum L.) seed germination response to temperature and water potential. Acta Physiol. Plant. 2017;39:250. doi: 10.1007/s11738-017-2549-8. [DOI] [Google Scholar]
- 35.Onofri A., Benincasa P., Mesgaran M.B., Ritz C. Hydrothermal-time-to-event models for seed germination. Eur. J. Agron. 2018;101:129–139. doi: 10.1016/j.eja.2018.08.011. [DOI] [Google Scholar]
- 36.Moltchanova E., Sharifiamina S., Moot D.J., Shayanfar A., Bloomberg M. Comparison of three different statistical approaches (non-linear least-squares regression, survival analysis and Bayesian inference) in their usefulness for estimating hydrothermal time models of seed germination. Seed Sci. Res. 2020;30:64–72. doi: 10.1017/S0960258520000082. [DOI] [Google Scholar]
- 37.Maguire J.D. Speed of Germination—Aid in Selection and Evaluation for Seedling Emergence and Vigor. Crop. Sci. 1962;2:176–177. doi: 10.2135/cropsci1962.0011183X000200020033x. [DOI] [Google Scholar]
- 38.Orchard T. Estimating the parameters of plant seedling emergence. Seed Sci. Technol. 1977;5:61–69. [Google Scholar]
- 39.Mubeen M., Bano A., Ali B., Islam Z.U., Ahmad A., Hussain S., Fahad S., Nasim W. Effect of plant growth promoting bacteria and drought on spring maize (Zea mays L.) Pak. J. Bot. 2021;53:2. doi: 10.30848/PJB2021-2(38). [DOI] [Google Scholar]
- 40.Ranal M.A., De Santana D.G., Ferreira W.R., Rodrigues C.M. Calculating germination measurements and organizing spreadsheets. Braz. J. Bot. 2009;32:849–855. doi: 10.1590/S0100-84042009000400022. [DOI] [Google Scholar]
- 41.Hafez M., Popov A.I., Rashad M. Integrated use of bio-organic fertilizers for enhancing soil fertility–plant nutrition, germination status and initial growth of corn (Zea mays L.) Environ. Technol. Innov. 2021;21:101329. doi: 10.1016/j.eti.2020.101329. [DOI] [Google Scholar]
- 42.Kader M. A comparison of seed germination calculation formulae and the associated interpretation of resulting data. J. Proceeding R. Soc. N. S. W. 2005;138:65–75. [Google Scholar]
- 43.Uddin S., Ullah S., Nafees M. Effect of seed priming on growth and performance of Vigna radiata L. under induced drought stress. J. Agric. Food Res. 2021;4:100140. doi: 10.1016/j.jafr.2021.100140. [DOI] [Google Scholar]
- 44.Kumar B., Verma S.K., Ram G., Singh H.P. Temperature Relations for Seed Germination Potential and Seedling Vigor in Palmarosa (Cymbopogon martinii) J. Crop Improv. 2012;26:791–801. doi: 10.1080/15427528.2012.689799. [DOI] [Google Scholar]
- 45.Salehzade H., Izadkhah Shishvan M., Chiyasi M. Effect of seed priming on germination and seedling Growth of Wheat (Triticum aestivum L.) J. Biol. Sci. 2009;4:629–631. [Google Scholar]
- 46.Hao J.-H., Lv S.-S., Bhattacharya S., Fu J.-G. Germination Response of Four Alien Congeneric Amaranthus Species to Environmental Factors. PLoS ONE. 2017;12:e0170297. doi: 10.1371/journal.pone.0170297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Xiao H., Yang H., Monaco T., Song Q., Rong Y. Modeling the influence of temperature and water potential on seed germination of Allium tenuissimum L. PeerJ. 2020;8:e8866. doi: 10.7717/peerj.8866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bakhshandeh E., Bradford K.J., Pirdashti H., Vahabinia F., Abdellaoui R. A new halothermal time model describes seed germination responses to salinity across both sub- and supra-optimal temperatures. Acta Physiol. Plant. 2020;42:137. doi: 10.1007/s11738-020-03126-9. [DOI] [Google Scholar]
- 49.Wang H., Zhao K., Li X., Chen X., Liu W., Wang J. Factors affecting seed germination and emergence of Aegilops tauschii. Weed Res. 2020;60:171–181. doi: 10.1111/wre.12410. [DOI] [Google Scholar]
- 50.Allen P.S., Meyer S.E., Khan M.A. Hydrothermal time as a tool in comparative germination studies. In: Black M., Bradford K.J., Vasquez-Ramos J., editors. Seed Biology: Advances and Applications. CABI Publishing; Wallingford, UK: 2000. pp. 401–410. [Google Scholar]
- 51.Rowse H., Finch-Savage W. Hydrothermal threshold models can describe the germination response of carrot (Daucus carota) and onion (Allium cepa) seed populations across both sub-and supra-optimal temperatures. New Phytol. 2003;158:101–108. doi: 10.1046/j.1469-8137.2003.00707.x. [DOI] [Google Scholar]
- 52.Derakhshan A., Bakhshandeh A., Siadat S.A.-A., Moradi-Telavat M.-R., Andarzian S.B. Quantifying the germination response of spring canola (Brassica napus L.) to temperature. Ind. Crop. Prod. 2018;122:195–201. doi: 10.1016/j.indcrop.2018.05.075. [DOI] [Google Scholar]
- 53.Windauer L.B., Martinez J., Rapoport D., Wassner D., Benech-Arnold R. Germination responses to temperature and water potential in Jatropha curcas seeds: A hydrotime model explains the difference between dormancy expression and dormancy induction at different incubation temperatures. Ann. Bot. 2011;109:265–273. doi: 10.1093/aob/mcr242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Shah W., Ullah S., Ali S., Idrees M., Khan M.N., Ali K., Khan A., Ali M., Younas F. Effect of exogenous alpha-tocopherol on physio-biochemical attributes and agronomic performance of lentil (Lens culinaris Medik.) under drought stress. PLoS ONE. 2021;16:e0248200. doi: 10.1371/journal.pone.0248200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bradford K.J. Applications of hydrothermal time to quantifying and modeling seed germination and dormancy. Weed Sci. 2002;50:248–260. doi: 10.1614/0043-1745(2002)050[0248:AOHTTQ]2.0.CO;2. [DOI] [Google Scholar]
- 56.Alam H., Khattak J.Z.K., Ksiksi T.S., Saleem M.H., Fahad S., Sohail H., Ali Q., Zamin M., El-Esawi M.A., Saud S., et al. Negative impact of long-term exposure of salinity and drought stress on native Tetraena mandavillei L. Physiol. Plant. 2020;172:1336–1351. doi: 10.1111/ppl.13273. [DOI] [PubMed] [Google Scholar]
- 57.Wijewardana C., Alsajri F.A., Reddy K.R. Soybean seed germination response to in vitro osmotic stress. Seed Technol. 2018;39:143–154. [Google Scholar]
- 58.Seepaul D.D.R., George S., Groot J., Wright D. Drought tolerance classification of common oilseed species using seed germination assay. J. Oilseed Brassica. 2019;10:97–105. [Google Scholar]
- 59.Nazar Z., Akram N., Saleem M., Ashraf M., Ahmed S., Ali S., Alsahli A.A., Alyemeni M. Glycinebetaine-Induced Alteration in Gaseous Exchange Capacity and Osmoprotective Phenomena in Safflower (Carthamus tinctorius L.) under Water Deficit Conditions. Sustainability. 2020;12:10649. doi: 10.3390/su122410649. [DOI] [Google Scholar]
- 60.Bradford K. Water relations in seed germination. In: Negbi M., Galili G., Kigel J., editors. Seed Development and Germination. Marcel Dekker; New York, NY, USA: 1995. pp. 351–396. [Google Scholar]
- 61.Mesgaran M., Onofri A., Mashhadi H.R., Cousens R.D. Water availability shifts the optimal temperatures for seed germination: A modelling approach. Ecol. Model. 2017;351:87–95. doi: 10.1016/j.ecolmodel.2017.02.020. [DOI] [Google Scholar]
- 62.Baath G.S., Kakani V.G., Gowda P.H., Rocateli A.C., Northup B.K., Singh H., Katta J.R. Guar responses to temperature: Estimation of cardinal temperatures and photosynthetic parameters. Ind. Crop. Prod. 2020;145:111940. doi: 10.1016/j.indcrop.2019.111940. [DOI] [Google Scholar]
- 63.Kurtar E.S. Modelling the effect of temperature on seed germination in some cucurbits. Afr. J. Biotechnol. 2010;9:1343–1353. doi: 10.5897/ajb2010.000-3016. [DOI] [Google Scholar]
- 64.Demir I., Mavi K. The effect of priming on seedling emergence of differentially matured watermelon (Citrullus lanatus (Thunb.) Matsum and Nakai) seeds. Sci. Hortic. 2004;102:467–473. doi: 10.1016/j.scienta.2004.04.012. [DOI] [Google Scholar]
- 65.Maynard D., Hochmuth G. Knott’s Handbook for Vegetable Growers. John Willy & Sons. Inc.; Hoboken, NJ, USA: 2007. [Google Scholar]
- 66.Alvarado V., Bradford K.J. A hydrothermal time model explains the cardinal temperatures for seed germination. Plant Cell Environ. 2002;25:1061–1069. doi: 10.1046/j.1365-3040.2002.00894.x. [DOI] [Google Scholar]
- 67.Atashi S., Bakhshandeh E., Zeinali Z., Yassari E., Da Silva J.A.T. Modeling seed germination in Melisa officinalis L. in response to temperature and water potential. Acta Physiol. Plant. 2013;36:605–611. doi: 10.1007/s11738-013-1436-1. [DOI] [Google Scholar]
- 68.Dahal P., Bradford K.J. Hydrothermal time analysis of tomato seed germination at suboptimal temperature and reduced water potential. Seed Sci. Res. 1994;4:71–80. doi: 10.1017/S096025850000204X. [DOI] [Google Scholar]
- 69.Atashi S., Bakhshandeh E., Mehdipour M., Jamali M., Da Silva J.A.T. Application of a Hydrothermal Time Seed Germination Model Using the Weibull Distribution to Describe Base Water Potential in Zucchini (Cucurbita pepo L.) J. Plant Growth Regul. 2014;34:150–157. doi: 10.1007/s00344-014-9452-y. [DOI] [Google Scholar]
- 70.Basit A., Khan S., Sulaiman S.S., Shah A.A. Morphological features of various selected tree species on the greater university campus Peshawar, Pakistan. Int. J. Bot. Stud. 2019;4:92–97. [Google Scholar]
- 71.Gareca E.E., Vandelook F., Fernández M., Hermy M., Honnay O. Seed germination, hydrothermal time models and the effects of global warming on a threatened high Andean tree species. Seed Sci. Res. 2012;22:287–298. doi: 10.1017/S0960258512000189. [DOI] [Google Scholar]
- 72.Bradford K.J., Still D.W. Applications of hydrotime analysis in seed testing. Seed Technol. 2004;26:75–85. [Google Scholar]
- 73.Nemeskéri E., Helyes L. Physiological Responses of Selected Vegetable Crop Species to Water Stress. Agronomy. 2019;9:447. doi: 10.3390/agronomy9080447. [DOI] [Google Scholar]
- 74.Ghafar M., Akram N., Saleem M., Wang J., Wijaya L., Alyemeni M. Ecotypic Morphological and Physio-Biochemical Responses of Two Differentially Adapted Forage Grasses, Cenchrus ciliaris L. and Cyperus arenarius Retz. to Drought Stress. Sustainability. 2021;13:8069. doi: 10.3390/su13148069. [DOI] [Google Scholar]