The effect of weak clonal interference on average fitness trajectories in the presence of macroscopic epistasis

Abstract

Adaptation dynamics on fitness landscapes is often studied theoretically in the strong-selection, weak-mutation regime. However, in a large population, multiple beneficial mutants can emerge before any of them fixes in the population. Competition between mutants is known as clonal interference, and while it is known to slow down the rate of adaptation (when compared to the strong-selection, weak-mutation model with the same parameters), how it affects the shape of long-term fitness trajectories in the presence of epistasis is an open question. Here, by considering how changes in fixation probabilities arising from weak clonal interference affect the dynamics of adaptation on fitness-parameterized landscapes, we find that the change in the shape of fitness trajectory arises only through changes in the supply of beneficial mutations (or equivalently, the beneficial mutation rate). Furthermore, a depletion of beneficial mutations as a population climbs up the fitness landscape can speed up the rescaled fitness trajectory (where adaptation speed is measured relative to its value at the start of the experiment), while an enhancement of the beneficial mutation rate does the opposite of slowing it down. Our findings suggest that by carrying out evolution experiments in both regimes (with and without clonal interference), one could potentially distinguish the different sources of macroscopic epistasis (fitness effect of mutations vs change in fraction of beneficial mutations).

Introduction

For unicellular organisms, as individuals in an asexual population gain mutations and increase in fitness, how their average fitness increases over evolutionary timescales [which we refer to as the average fitness trajectory F(t)] depends on the distribution $\rho (s)$ of fitness effects s of potential new mutations (i.e. mutations that can potentially occur). This distribution may change as a population evolves, an effect known as macroscopic epistasis (Fig. 1a) (Good and Desai 2015). This could come about, for example, when the fitness effects of mutations depend on the state of other genes or the presence of other mutations (Chou et al. 2011; Khan et al. 2011; Wang et al. 2013). The effect of such changes in $\rho (s)$ on fitness trajectories has been studied in the context of fitness-parameterized landscapes, where $\rho (s|x)$ is assumed to depend only on the fitness x of the cell (Kryazhimskiy et al. 2009; Good and Desai 2015).

Fig. 1.

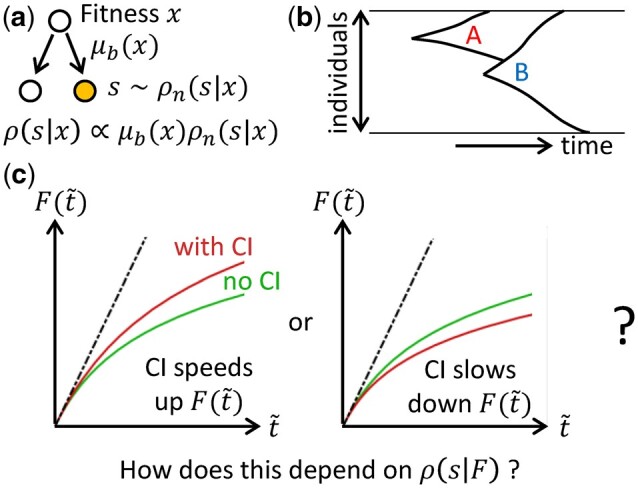
Schematic of the model and the question-of-interest. a) Whenever a cell divides, there is a probability ${\mu }_b(x)$ of it gaining a beneficial mutation which can depend on the fitness x of the cell. When a beneficial mutation occurs, we assume that the selection coefficient s of the mutation is drawn from some normalized distribution ${\rho }_n(s|x)$ which can also depend on x. The overall distribution $\rho (s|x)$ of beneficial selection coefficients when a mutation occurs specifies the fitness-parameterized landscape, or equivalently, the form of macroscopic epistasis. b) Clonal interference refers to the phenomenon where a mutant (“A,” already growing exponentially in size) is out-competed by a new mutant (“B”) with a higher selective advantage. c) The functional forms of the average fitness trajectories F(t) are compared after rescaling time such that the initial adaptation speeds are identical. We ask whether clonal interference speeds up (left) or slows down (right) the functional form of the average fitness trajectory, and how this depends on $\rho (s|F)$.

Within this framework, adaptation dynamics observed experimentally can be used to infer features of the underlying fitness landscape or equivalently, the type of epistasis present in the system (Wiser et al. 2013; Kryazhimskiy et al. 2014; Good and Desai 2015). The shape of fitness trajectories (which we characterize using its functional form) is typically studied theoretically in the strong-selection, weak-mutation (SSWM) regime, in which the time for beneficial mutations to fix is much shorter than the time for successful beneficial mutations to emerge (Desai and Fisher 2007). However, in large populations, multiple beneficial mutants can emerge before any of them fixes. Competition between beneficial mutants in different lineages is known as clonal interference (Fig. 1b) and has been shown to reduce fixation probabilities (Gerrish and Lenski 1998; Lin et al. 2020), and hence slow down adaptation rate when compared to the SSWM model with the same parameters. There have also been suggestions that clonal interference slows down the form (i.e. shape) of fitness trajectories (Wiser et al. 2013) (here, we are interested in the functional forms of the fitness trajectories, and therefore the trajectories are compared after scaling time such that they have identical initial slopes—we consider a trajectory to be slower than another if it has a slower fitness increase after this re-scaling, Fig. 1c). In particular, the slow fitness trajectory observed in Lenski’s long-term evolution experiment (where the fitness appears to continue increasing over a long period of time without reaching any plateau) was previously attributed to both diminishing returns epistasis and clonal interference (Wiser et al. 2013). However, the relative contributions from these two factors have not been explored, and it is not clear if it is generally the case that clonal interference slows down the form of fitness trajectories in the presence of epistasis.

Here, by considering how changes in fixation probabilities arising from weak clonal interference affect the dynamics of adaptation on fitness-parameterized landscapes, we find that the change in the form of fitness trajectory due to clonal interference arises only through changes in the supply of beneficial mutations (or equivalently, the beneficial mutation rate), independent of any changes in the average fitness effect of beneficial mutations. This implies that as long as the fraction of beneficial mutations stays the same, the functional form of the fitness trajectory will be the same with or without clonal interference, even if the mean fitness effect of beneficial mutations decreases over time (i.e. diminishing returns). Furthermore, a depletion of beneficial mutations as a population climbs up the fitness landscape can speed up the functional form of the fitness trajectory (while an enhancement of the beneficial mutation rate slows it down). These findings suggest that by carrying out evolution experiments in both regimes (with and without clonal interference), one could potentially distinguish the different sources of macroscopic epistasis (change in fitness effects of mutations vs change in the fraction of beneficial mutations).

Results

We consider the Moran process, where a population has a constant size N, and each cell divides at some rate which we call the fitness of the cell. Whenever a cell divides, a random cell is simultaneously removed from the population. Experimentally, this corresponds, approximately, to growing cells in a continuous culture (e.g. in a turbidostat) (Bryson and Szybalski 1952; Moran et al. 1964). During each division event, there is some probability that the daughter cell gains a new mutation (Fig. 1a). We assume that the fitness effects of deleterious mutations are typically much larger than those of beneficial ones, such that beneficial mutations rarely compensate deleterious mutations, and hence deleterious mutations cannot fix. The adaptation of the population is therefore driven by the probability μ_b of gaining a beneficial mutation during division, which is a dimensionless quantity that we will refer to as the beneficial mutation rate.

Inspired by previous theoretical studies (Gillespie 1984; Orr 2003), we assume an exponential distribution for the fitness effects of beneficial mutations. Such a distribution also seems to have some experimental support (Imhof and Schlötterer 2001; Rokyta et al. 2005; Kassen and Bataillon 2006). Nevertheless, there are other data that suggest otherwise (Rokyta et al. 2008; Levy et al. 2015), and we show in Appendix B and Appendix C that our main conclusions hold for a more general class of distributions. Generalizing the approach of Kryazhimskiy et al. (2009), given the current fitness of a cell x, the distribution of its beneficial mutant fitness values y > x is assumed to be given by:

$${\Phi }_x(y)=f(x)e^{-f(x)(y-x)}{e}^{-h(x)}$$ (1)

where $\frac{1}{f(x)}$ represents how the mean fitness effects $(y-x)$ of mutations vary with current fitness, and h(x) governs how the fraction of beneficial mutations changes with the current fitness of the cell. The beneficial mutation rate is then given by ${\mu }_b(x)={\mu }_{b0}{e}^{-h(x)}$, with ${\mu }_{b0}$ being the initial beneficial mutation rate.

For any ${\Phi }_x(y)$, the corresponding distribution of fitness selection coefficients $s=\frac{y-x}{x}$ is then given by

$$\rho (s|x)=\alpha (x)e^{-\alpha (x)s}{e}^{-h(x)},$$ (2)

where $\alpha (x)=xf(x)={\langle s\rangle }^{-1}$ is the inverse of the mean selection coefficient of beneficial mutations. Within this model, macroscopic epistasis can act through changing the mean of beneficial mutation effects as the population increases in fitness, through changing the availability of new beneficial mutations, or a combination of both.

This framework reduces back to other previously known models for specific forms of f(x) (or equivalently, $\alpha (x)$) and h(x). For example, the House of cards (HoC)/Uncorrelated fitness landscape is the case where ${\Phi }_x(y)$ is independent of x and corresponds to $f(x)\sim 1$ and $h(x)\sim x$ (Kryazhimskiy et al. 2009). This implies that while the absolute mean fitness increase conferred by mutations stay the same, the availability of beneficial mutations decreases exponentially as fitness increases. Similarly, the nonepistatic (NEPI) fitness landscape is the case where the distribution of fitness effects of mutations is independent of genotype, i.e. ${\Phi }_x(y)$ is only a function of $y––x$ (Kryazhimskiy et al. 2009), which corresponds to having $f(x)\sim 1$ and h(x) = 0. The Stairway to heaven (STH) fitness landscape (Kryazhimskiy et al. 2009) is the case where $\rho (s)$ is independent of fitness, and corresponds to having $\alpha (x)\sim 1$ while h(x) = 0. The diminishing returns epistasis model adopted by Wiser et al. (2013) can also be mapped to this fitness-parameterized framework with $\alpha (x)\sim x^g$ for $g\gg 1$ and h(x) = 0.

We assume that the beneficial mutation rate is not too large such that the population is typically in a monomorphic state. When a new beneficial mutation with fitness effect s emerges, it fixes with some probability $P_f(s)$. The average fitness trajectory F(t) on such fitness-parametrized landscapes is then approximately given by (Kryazhimskiy et al. 2009):

$$\frac{dF}{dt}=N{F}^2{\mu }_{b0}{\int }_0^{\infty }s{P}_f(s)\rho (s|F)ds,$$ (3)

where time t here refers to real time (i.e. the actual amount of time that has passed in a continuous culture), in contrast to being the number of generations often considered in other studies (Kryazhimskiy et al. 2009; Wiser et al. 2013). This definition of time is why, compared to those previous studies, we have an additional factor of F in the equation (since we have defined fitness to be the growth rate, such that the number of generations in a small time interval δt is $F(t)\delta t$).

In the SSWM regime [$N{\mu }_b\hspace{0.17em}\text{log}(Ns)\ll 1$ (Desai and Fisher 2007)], $P_f(s)=\pi (s)\approx s$. Substituting $\rho (s|F)$ from Equation (2) and defining $\tilde{s}=\alpha s$ (the selection coefficient of a mutation relative to the average selection coefficient), the dynamics of fitness in this regime are given by:

$$\begin{array}{c}\frac{d\hspace{0.17em}\text{log}(F)}{dt}=\frac{NF{\mu }_{b0}{e}^{-h(F)}}{{\alpha }^2(F)}{\int }_0^{\infty }{\tilde{s}}^2{e}^{-\tilde{s}}d\tilde{s}\hfill \\ =2\frac{NF{\mu }_{b0}{e}^{-h(F)}}{{\alpha }^2(F)},\hfill \end{array}$$ (4)

where the functional form of the fitness trajectory depends on the type of epistasis specified through $\alpha (F)$ and h(F). For example, the HOC landscape ($h(F)\sim F,\hspace{0.17em}\alpha (F)\sim F$) gives $F(t)\sim \hspace{0.17em}\text{log}(t)$, the NEPI landscape (h(F) = 0, $\alpha (F)\sim F$) gives $F(t)\sim t$, and the STH landscape ($\alpha (F)\sim 1$, h(F) = 0) gives a function F(t) that increases faster than linearly. The diminishing returns model ($\alpha (F)\sim F^g$, h(F) = 0) by Wiser et al. gives a power law trajectory with exponent $\frac{1}{2g-1}$. (Note that this exponent is slightly different from that in Wiser et al. because of the difference in how time is defined. Also, in Wiser et al. clonal interference is taken into account in addition to the assumption of the diminishing returns model. We will show later that taking into account clonal interference has no effect on this exponent.)

When a population is sufficiently large, after a mutation has escaped loss via genetic drift and the number of mutants starts to increase deterministically, there is some probability that another new successful mutation emerges in the resident population while the first mutant is still in the process of taking over the population. The second mutant could then potentially out-compete the first mutant, causing the first mutation to go extinct. (Note that if a second mutation were to occur in a cell that already contains the first mutation, it is not considered an interfering mutation because if the second mutation were to fix, the first mutation would fix along with it. In this case, we also assume that this second mutation does not affect the fixation probability of the first mutation since the first mutant was already on its way to fixation even without the second mutation.) Following the approach in Gerrish and Lenski, for a mutant that emerges in a clonal population containing individuals with fitness F, the probability of it fixing, $P_f(s)$ , will then be the probability that it escapes loss via genetic drift (and would go on to fix in the absence of any interference), $\pi (s)$, and not out-competed by any other mutation that could potentially emerge in the background population while the first mutant population is growing in size:

$$P_f(s)=\pi (s)e^{-{\int }_0^T{R}_I(\tilde{t})d\tilde{t}},$$ (5)

where $T\approx \frac{2\hspace{0.17em}\text{log}(N)}{s}$ is the average number of generations it takes for a mutant to fix without any interference (assuming deterministic, logistic growth of the mutant strain). $R_I(\tilde{t})$ is the rate at which a successful interfering mutation emerges at generation $\tilde{t}$ after the first mutant sub-population starts growing in size, and is given by the rate at which the resident population gains another more beneficial mutation which subsequently goes on to fix:

$$R_I(\tilde{t})=N{\mu }_{b0}n(\tilde{t}){\int }_s^{\infty }\rho (s_I|F)p_f(n(\tilde{t})|s,s_I)d{s}_I,$$ (6)

where $n(\tilde{t})=\frac{(N-1)e^{-s\tilde{t}}}{1+(N-1)e^{-s\tilde{t}}}$ is the fraction of resident cells (again from logistic growth of the mutant strain), $\rho (s_I|F)$ is the distribution of fitness effects of mutations that can arise in a cell with fitness F (Equation 2), and $p_f(n(\tilde{t})|s,s_I)$ is the fixation probability of the interfering mutant with fitness effect s_I. Intuitively, we expect $p_f(n|s,s_I)$ to increase with n since the closer the first mutant is to fixing (i.e. lower n), the harder it is for the new mutant to outcompete the original mutant. In particular, one might also expect the probability of the interfering mutant fixing in this mixed population to be the same as that in a clonal population with the same average population growth rate (i.e. all cells grow at this rate). We will show that this is indeed true for all n when the growth rate of the mutant is much larger than that of the population-averaged growth rate (but not in general).

Assuming that clonal interference is weak such that at most one successful competing mutation occurs during the time a mutant is trying to fix (i.e. no further mutations occur after the emergence of the second mutant), the extinction probability $p_{\mathit{ext}}(n)$ of the new (interfering) mutant (in the large N limit) can be found by considering the different events that can happen (different cell types dividing and leaving the population) in the next time step and requiring all remaining mutants to go extinct (Appendix A). The fixation probability $p_f(n)=1-p_{\mathit{ext}}(n)$ is then found to be given by the solution to the following equation (Appendix A):

$$\begin{array}{c}(1+s_I)p_f^2(n)+(s(1-n)-s_I)p_f(n)-\frac{D(n)}{2}\frac{{\partial }^2{p}_f(n)}{{\partial }^{2}n}+v(n)\frac{\partial p_f(n)}{\partial n}=0,\hfill \end{array}$$ (7)

where $D(n)=\frac{n(1-n)}{N}(2+s)$ and $v(n)=n(1-n)s$, and the boundary conditions are given by $p_f(0)=(s_I-s)/(1+s_I)$ and $p_f(1)=s_I/(1+s_I)$, which are also the fixation probabilities of a mutant in a clonal population within the Moran process (Moran et al. 1964; Nowak 2006).

When the first two terms in Equation (7) dominate (either when n is close to 0 or 1, or when $s_I\gg s$), we recover the intuitive result that the fixation probability is the selective advantage of the interfering mutant over that of the population average:

$$p_f(n)\approx s_I-s(1-n),$$ (8)

where we have also taken the limit where fitness effects are generally small $s,s_I\ll 1$. For simplicity and concreteness, we will assume this specific form for $p_f(n)$ in the rest of the paper, but we argue in Appendix B that adopting the more general solution of Equation (7) does not affect our main conclusions.

Within this approach, we have considered the effect of potential interfering mutants on the fixation probability of a mutant that initially arose in a clonal population. This implicitly assumes that clonal interference is sufficiently weak that most of the time a mutation emerges when the population is dominated by a single subgroup. We elaborate on this assumption more extensively in the Discussion section.

The dynamics of fitness in the presence of weak clonal interference is therefore given by (using Equations [3], [5], [6], [8], see Appendix B):

$$\frac{d\hspace{0.17em}\text{log}(F)}{dt}=\frac{NF{\mu }_{b0}{e}^{-h(F)}}{{\alpha }^2(F)}{\int }_0^{\infty }{\tilde{s}}^2{e}^{-(\tilde{s}+\lambda (\tilde{s},F))}d\tilde{s},$$ (9)

where, in the limit $\text{log}(N)\gg 1$,

$$\lambda (\tilde{s},F)\approx N\hspace{0.17em}\text{log}(N){\mu }_{b0}{e}^{-h(F)}\left(\frac{1}{\tilde{s}}+1\right)e^{-\tilde{s}}.$$ (10)

If the beneficial mutation rate does not depend on fitness [h(F) = 0], we recover the same expression for $\lambda (\tilde{s})$ derived by Gerrish and Lenski (1998).

In the following section, we will explore the effect of clonal interference on the functional form (i.e. shape) of the average fitness trajectory by comparing the dynamics with (Equation 9) and without (Equation 4) clonal interference. When comparing the numerical solutions of Equations (4) and (9), we scale time in the case with clonal interference by a factor such that $\frac{d{F}_{\text{CI}}}{d\tilde{t}}{|}_{t=0}=\frac{d{F}_{\text{noCI}}}{dt}{|}_{t=0}$ (since we are interested in comparing functional forms rather than the absolute time dynamics).

To verify our findings, we also carried out full Gillespie simulations of the Moran process, where we keep track of the fitness values of all cells, with the probability of a cell dividing proportional to its fitness (see Appendix D for simulation details). When a mutation event occurs during division, the fitness effect of the mutation is drawn from a distribution based on the fitness of the dividing cell. Within each simulation, the mean population fitness at any time is obtained from an average over all cells in the population. We show in Fig. A2 that the fitness trajectory given by Equation (9) agrees well with our simulation data over a range of mutation rates.

Change in functional form of fitness trajectory only depends on how beneficial mutation rate changes

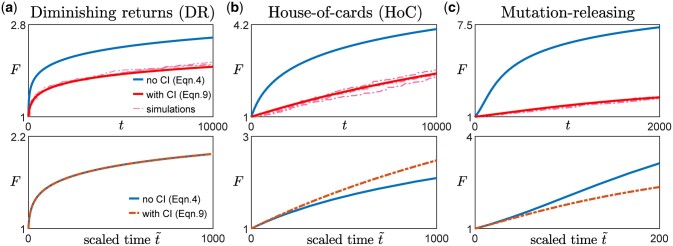
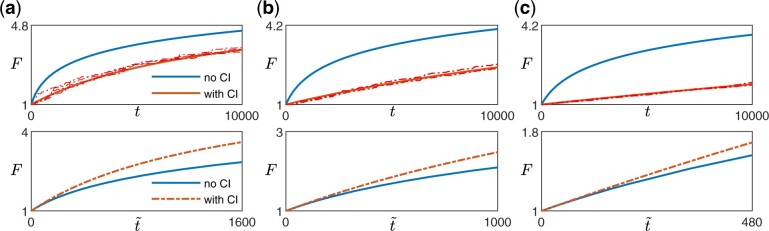
Since any additional dependence on F due to the clonal interference term comes only from h(F) (Equations 9 and 10), we expect weak clonal interference to only affect the functional form of the fitness trajectory if the beneficial mutation rate ${\mu }_b={\mu }_{b0}{e}^{-h(F)}$ changes with fitness (Figs. 2 and A2). In other words, if $h(F)\sim O(1)$ (such as in the case of the diminishing returns model and the STH landscape), even if there is epistasis that acts through $\alpha (F)$, clonal interference does not change the functional form of the trajectory (Fig. 2a, left panel in Fig. A2). This is the case because as long as the availability of beneficial mutations does not change, the presence of clonal interference reduces the rate of fitness increase by the same amount at all times.

Fig. 2.

Effect of clonal interference on fitness trajectory for different types of macroscopic epistasis. a) Within the diminishing returns model where the mean fitness effect of beneficial mutations decreases with fitness but the beneficial mutation rate stays the same, the functional form of the fitness trajectory stays the same. The upper panels show the fitness trajectories as a function of actual time t with (red) and without (blue) clonal interference. The solid lines are obtained from solving Equations (4) and (9), while the dashed lines (pink) are individual replicates from simulations. The lower panels compare trajectories (blue and red solid lines in the upper panel) after rescaling time $\tilde{t}=At$ for the case with clonal interference, with A being a constant chosen such that both trajectories have the same derivative at $\tilde{t}=0$. [Landscape parameters: $\alpha (F)=20F^5,\hspace{0.17em}{\mu }_b={\mu }_{b0}$] b) With the House-of-Cards/uncorrelated landscape where the mean fitness effects of beneficial mutations stays the same but the beneficial mutation rate decreases with fitness, the presence of clonal interference speeds up the functional form of the fitness trajectory. [Landscape parameters: $\alpha (F)=100F,\hspace{0.17em}{\mu }_b={\mu }_{b0}{e}^{-(F-1)}$] c) With a mutation-releasing landscape where the beneficial mutation rate increases with fitness, the presence of clonal interference slows down the functional form of the fitness trajectory. [Landscape parameters: $\alpha (F)=50e^{F-1},\hspace{0.17em}{\mu }_b={\mu }_{b0}{e}^{F-1}$.] [Other parameters in a–c): $N={10}^6,\hspace{0.17em}{\mu }_{b0}=1·{10}^{-5}$.]

If h(F) depends on F, whether the form of the trajectory is sped up or slowed down by clonal interference depends on whether h(F) increases or decreases with F. In many commonly used and widely studied models of fitness landscapes, h(F) increases with F, i.e. the beneficial mutation rate decreases with fitness. For example, in the HOC landscape, a new fitness value is drawn from the same distribution whenever a mutation occurs (Park and Krug 2008; Kryazhimskiy et al. 2009), implying that as fitness increases, the probability of drawing a higher value of fitness (for the mutant) decreases. In Fisher’s geometric model (Fisher 1930), the state of the cell lies in a multidimensional phenotypic space, with a certain point being the optimal phenotype, such that the fitness is specified by how close the state of the cell is to the optimal state. Mutations then correspond to drawing random vectors in the space. Within this model, the probability of a mutation providing an improvement (i.e. bringing the population closer to the optimal state) also decreases with fitness (Fisher 1930; Hartl and Taubes 1996; Ram and Hadany 2015). In these cases where h(F) increases with F, clonal interference speeds up the functional form of the trajectory (Fig. 2b, middle panel in Fig. A2). Intuitively, this occurs because as fitness increases, the effect of clonal interference is reduced since there are fewer potential beneficial interfering mutations. This phenomenon was previously described in Park and Krug (2008).

Similarly, in the opposite case where h(F) decreases with F, there are more potential beneficial mutations as the population climbs up the fitness landscape (one could imagine this happening if gaining certain mutations opens up more beneficial mutational paths). In this case, interfering mutations become more common as the population evolves and the form of the trajectory is slowed down by such an effect (Fig. 2c, right panel in Fig. A2).

Besides the average fitness trajectory, we find that these general arguments and results also hold for the average substitution trajectory, i.e. how the average number of fixed mutations increases over time, when $N{\mu }_{b0}$ is sufficiently small (Appendix E). However, there is a regime where this theory underestimates the number of accumulated mutations while still providing good predictions for the average fitness, suggesting that the excess mutations arise from nearly neutral mutations (Appendix E). We return to this point in the Discussion section.

Proposed experimental protocol for determining how beneficial mutation rate changes

To determine whether and how the availability of beneficial mutations changes over time (with fitness), one can carry out two or more sets of long-term evolution experiments at different population sizes or mutation rates (Sprouffske et al. 2018) spanning both the SSWM regime and the regime with weak clonal interference (Fig. 3a). N can be varied, for example, by carrying out experiments in a turbidostat at different optical densities, while potential ways of varying the overall mutation rate μ (i.e. the probability of gaining a mutation per division) include changing the expression levels of DNA repair enzymes, such as mutH (Sherer and Kuhlman 2020) and Ada (Uphoff et al. 2016) in Escherichia coli, and inducing mutagenesis using UV radiation (Shibai et al. 2017). If N is the variable being varied, it would be useful to first measure the mutation rate of the initial strain (e.g. by carrying out the Luria Delbruck fluctuation test) if it is not already known, as this would provide an upper bound for ${\mu }_{b0}$. This can inform the possible choices of N for the experiment. For example, if $N\approx 1/\mu$ [and assuming that N is large enough so that fixation of deleterious mutations via genetic drift can be neglected, although in general it may not be true (Silander et al. 2007; Kryazhimskiy et al. 2012)] it would almost certainly be in the SSWM regime, and one can then adopt increasingly large values of N. [One could also sequence samples of the population at regular intervals during the initial stage of the experiment to extract the allele frequency trajectories of all detected mutations (Good et al. 2017)—predominantly nonoverlapping selective sweeps would indicate that the population is initially either in the SSWM or weak clonal interference regime.] The average fitness trajectory for a given N and μ can then be obtained by averaging over the replicates in the corresponding set of experiments (Fig. 3b). In general, the initial rate of fitness increase will differ between sets of experiments (Fig. 3b). For an experimentally obtained average trajectory (where fitness values are obtained at discrete time points), the initial gradient $F\prime (0)$ can be estimated by extracting the time point t_c at which the measured fitness $F(t_c)$ first exceeds some value F_c (Fig. 3b). The initial gradient can then approximated by $F\prime (0)\approx \frac{F(t_c)-1}{t_c}$, where we have implicitly assumed that the trajectory is sufficiently well sampled that $F(t_c)$ is not much larger than F_c, i.e. $F(t_c)-F_c<{ϵ}_F$ with ϵ_F controlling the desired time resolution $\Delta t$. Since the upper bound to the initial gradient is $2N{\mu }_{b0}/{\alpha }_0^{\mathrm{2}}$ (Equations 4 and 9), a conservative choice would be for $\Delta t\le \frac{{ϵ}_F{\alpha }_0^{\mathrm{2}}}{2N{\mu }_{b0}}$ —often α₀ and ${\mu }_{b0}$ are a priori unknown in which case one could start with conservative estimates, take fitness measurements more frequently initially and adapt the measurement frequency as the experiment progresses. Scaling time for each trajectory by a factor proportional to $F\prime (0)$ such that all scaled fitness trajectories have approximately the same initial derivative (Fig. 3, c–e), one can then infer how μ_b changes. In particular, if the different trajectories overlap (or are statistically indistinguishable), it would suggest that μ_b remains approximately constant (Fig. 3c). If instead the scaled trajectories speed up (slow down) as N or the overall mutation rate is increased, it would suggest that μ_b decreases (increases) as fitness increases over time (Fig. 3, d and e). Note that since we are comparing the scaled trajectories, the different sets of experiments (with different N or μ) should be run to approximately the same final F rather than for the same period of time (i.e. for smaller N or μ, the experiment should run longer for fitness to increase to the same level). The trajectories should also be sufficiently long for any effect of epistasis (occurring through $\alpha (F) {\mu }_b(F)$) to be captured (since the strength of epistasis that can be detected depends on the range of F spanned by the trajectory).

Fig. 3.

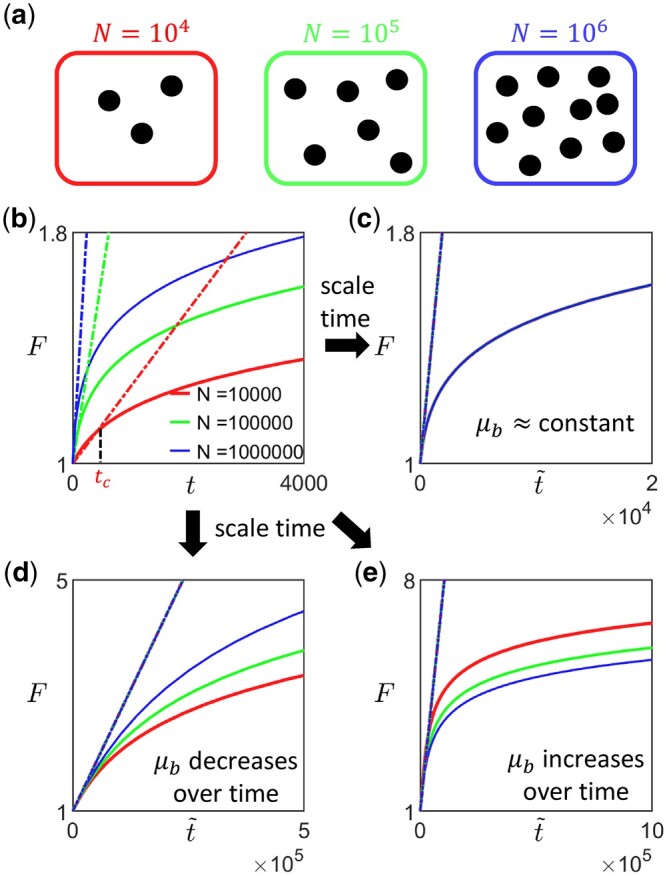
Proposal for experimental protocol to determine how the availability of beneficial mutation changes as fitness increases. a) The first step is to carry out multiple sets of long-term evolution experiments at different population sizes or mutation rates that span both the SSWM regime and the regime with weak clonal interference. For example, if the initial strain has estimated beneficial mutation rate ${\mu }_{b0}\approx {10}^{-5}$, one could carry out experiments with $N={10}^4,\hspace{0.17em}N={10}^5$, and $N={10}^6$. b) For each set of experiment (with a given N), one can then then obtain the average fitness trajectory by averaging over multiple replicates in each set (solid lines), and calculate the corresponding initial rate of fitness increase (dashed lines). c–e) By scaling time ($\tilde{t}=At$) such that the average trajectories have the same initial derivative, one can then infer how the beneficial mutation rate changes over time. c) If the scaled trajectories approximately overlap for all values of N, it would suggest that μ_b remains approximately constant. d) If the scaled trajectories speed up as N is increased, it would suggest that μ_b decreases as fitness increases over time. e) If the scaled trajectories slow down as N is increased, it would suggest that μ_b increases as fitness increases over time.

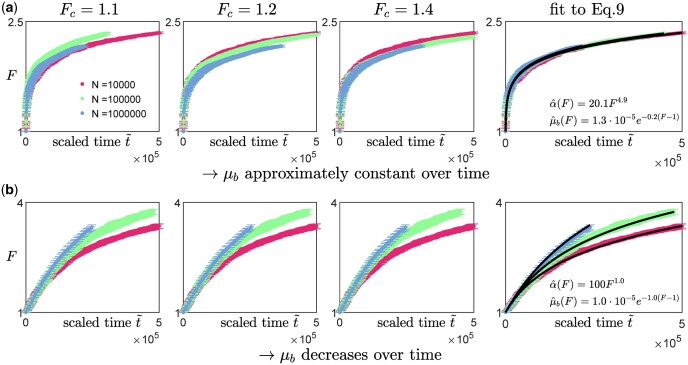
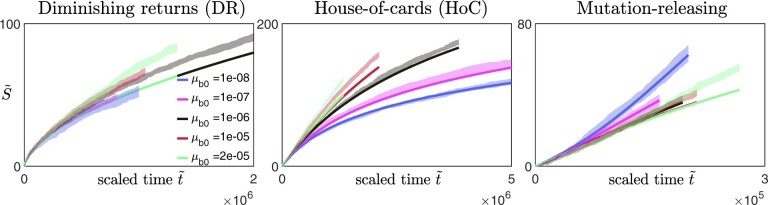
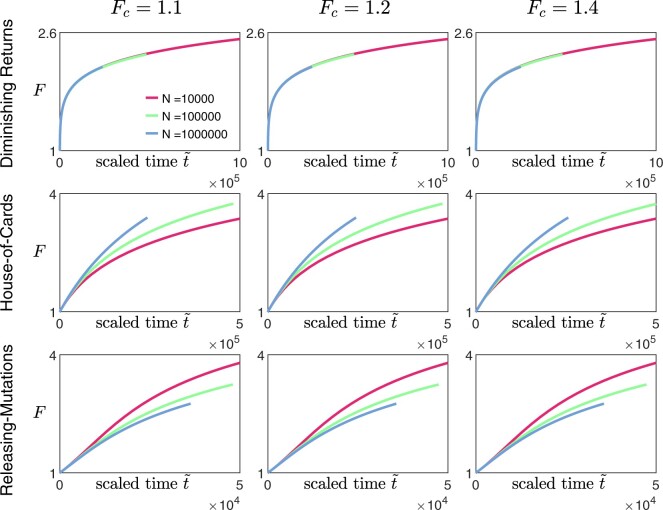
To test this protocol, we applied it on synthetic data obtained from our numerical simulations (Fig. 4, three leftmost columns). We coarsely sample the fitness trajectories, such that the time between successive measurements is at least a hundred (with the initial growth rate set to be 1), and focus on analyzing data from the diminishing-returns (Fig. 4a) and the House-of-cards landscapes (Fig. 4b). We find that the qualitative observation of how the shape of the trajectories changes with N remains approximately the same across different values of F_c (Fig. 4, three leftmost columns), suggesting that the inference is robust to how the initial fitness gradients are estimated. This is also consistent with the effect of varying F_c when rescaling trajectories obtained from solving Equation (9) (Appendix F, Fig. A5). In practice, experimental data could be noisier, and it would be useful to compare the trajectories using multiple values of F_c to ensure that any trends remain consistent.

Fig. 4.

Inferring the type of epistasis from synthetic data obtained from simulations on a) a diminishing-returns landscape with $\alpha (F)=20F^5$ and ${\mu }_b={\mu }_{b0}=1\times {10}^{-5}$, and b) a House-of-Cards/uncorrelated landscape with $\alpha (F)=100F$ and ${\mu }_b={\mu }_{b0}{e}^{-(F-1)}$ using different values of N. The time between successive measurements is at least a hundred (with the initial growth rate set to be 1), and each data point represents the average over 10 replicates with the error bars indicating the 95% confidence interval around the mean. The first 3 columns (from the left) are scaled trajectories obtained with different values of F_c used for estimating the initial fitness gradient. In both a) and b), how the shape of the trajectories change with N remains approximately consistent across all values of F_c, suggesting that the qualitative results are robust to how the initial fitness gradients are obtained. The last, right-most column show scaled trajectories where the initial fitness gradients are estimated from fitting the trajectories to Equation (9) assuming that the landscape takes the following form: $\alpha (F)={\alpha }_0{F}^{\varphi }$ and ${\mu }_b(F)={\mu }_{b0}{e}^{-\gamma (F-1)}$, with α₀, $\varphi ,\hspace{0.17em}{\mu }_{b0}$ and γ being free parameters used in the fitting. The solid black lines represent the fits to the data, while the inferred landscapes $\widehat{\alpha }(F)$ and $\widehat{{\mu }_b}(F)$ are shown in the insets. Based on how the shape of the scaled trajectories vary with N, one would infer that μ_b remains relatively constant in a) and decreases over time in b).

An alternative way of extracting the initial gradient would be to fit the trajectories directly to Equation (9). We assume that $\alpha (F)={\alpha }_0{F}^{\varphi }$ and $h(F)=\gamma (F-1)$ such that ${\mu }_b(F)={\mu }_{b0}{e}^{-\gamma (F-1)}$, and treat α₀, $\varphi ,\hspace{0.17em}{\mu }_{b0}$ and γ as parameters of the cell to be inferred from the fitness trajectories. We find that minimizing the least-squares error between the synthetic data and the trajectories obtained from solving Equation (9) allows a good recovery of the underlying landscape parameters (Fig. 4, right column). While these parameters already directly provide information about the type of epistasis present, they also allow a direct calculation of the initial fitness gradient (using Equation 9) which can again be used for visualizing the scaled trajectories (Fig. 4, right column). It is important to note that this approach requires the assumption of some general form for $\alpha (F)$ and h(F) which we typically have no knowledge of. Nevertheless, this fitting procedure can still be potentially useful for testing specific classes of landscapes and for distinguishing the relative types of epistasis (e.g. by comparing the magnitudes of $\varphi$ and γ).

Discussion

In the SSWM regime, different types of epistasis have been known to give very similar fitness trajectories. For example, both the HoC landscape (where the mean fitness effect stays the same but beneficial mutations deplete exponentially with fitness) and diminishing returns epistasis with constant beneficial mutation rates can give rise to a slow, approximately logarithmic fitness trajectory that does not seem to approach any plateau. Our results suggest that one way of distinguishing whether it is the average fitness effects of potential mutations or the average fraction of available mutations (or both) that is changing over time is to carry out the same set of evolution experiments with two or more different population sizes (Kryazhimskiy et al. 2012) or mutation rates (Sprouffske et al. 2018) (in both the SSWM regime and the regime with weak clonal interference), and compare their fitness trajectories.

Although we have only considered adaptation dynamics on fitness-parameterized landscapes, it is possible for such macroscopic epistasis to arise from a microscopic model of fitness landscape that explicitly takes into account interactions between genes (i.e. microscopic epistasis) (Guo et al. 2019; Reddy and Desai 2021). Furthermore, in many of these microscopic models, the rate of beneficial mutations decreases as the population climbs up the fitness landscape. In fact, such depletion of beneficial mutations also occurs when one models the genome as a finite sequence of sites, each having its own independent contribution to fitness [i.e. no microscopic epistasis, in which case F(t) approaches a maximum F_max according to a power law $F_{\mathit{max}}-F(t)\sim 1/t^2$ in the SSWM regime if the independent contributions to fitness follows an exponential distribution] (Good and Desai 2015). Our results therefore suggest that clonal interference can speed up the functional form of fitness trajectories even in these microscopic models.

Even though we have neglected the accumulation of deleterious mutations, if the selection coefficients of deleterious mutations are typically much larger than that of beneficial ones, one might consider the effect of deleterious mutations as decreasing the fraction of cells that can gain successful beneficial mutations (Fisher 1930; Orr 2000). When the deleterious mutation rate is much higher than that of beneficial mutations, the system can be thought of as being in a quasi-equilibrium state (mutation-selection balance), with the fraction of cells having the highest fitness (i.e. free of deleterious mutations) being $P_0=e^{-\frac{{\mu }_d}{s_d}}$, where μ_d is the deleterious mutation rate, and s_d is the harmonic mean of the distribution of fitness effects of deleterious mutations (Orr 2000). In the presence of macroscopic epistasis, μ_d, s_d, and hence P₀ can potentially depend on the fitness of the cell. Since successful interfering mutations can only arise in the fraction of resident population that is free of deleterious mutations, there would be an additional factor of $P_0(F)$ in the expression for $\lambda (\tilde{s},F)$ (Equation 10), which could further affect the shape of F(t) (Equation 9) in the presence of clonal interference (relative to that in the SSWM regime). Nevertheless, if s_d is independent of F, since ${\mu }_d(F)=\mu -{\mu }_b(F)$ (with μ being the constant probability of gaining a mutation per division), $P_0(F)$ changes (i.e. increases or decreases) with F in the same way as ${\mu }_b(F)$. This implies that the effect of $P_0(F)$ in terms of slowing or speeding up the shape of the trajectory is the same as that of ${\mu }_b(F)$. In general, s_d could vary with F and this could potentially be inferred by comparing fitness trajectories obtained with different μ (since this would change the contribution from P₀).

If instead the effects of deleterious mutations are typically weak, one needs to take into account the possibility of beneficial mutants emerging in backgrounds other than the fittest subgroup, and that a beneficial mutant that further accumulates deleterious mutations might still be able to fix (Johnson and Barton 2002; Pénisson et al. 2017; Jain 2019). In the limit where the selection coefficients of deleterious mutations are very weak ($s_d\to 0$), the probability $\pi (s)$ of a beneficial mutation with selection coefficient s surviving drift can be approximated by a step function at $s={\mu }_d$ (Johnson and Barton 2002; Pénisson et al. 2017; Jain 2019), such that $\pi (s)=0$ for $s<{\mu }_d$ while remaining unchanged ($\pi (s)\approx s$) for larger values of s. In this case, the lower bound of s in the integral in Equation (3) would be ${\mu }_d(F)$, and the corresponding lower bounds for both the integrals in Equations (4) and (9) would be ${\mu }_d(F)\alpha (F)$. The factor of $\alpha (F)$ in the lower bound suggests that even if μ_d is independent of F, epistasis acting through $\alpha (F)$ can potentially change the relative shape of the fitness trajectories with and without clonal interference. In particular, as $\alpha (F)$ increases with F (representing a decrease in the mean selection coefficient of beneficial mutations), the increase in the lower bound implies that the effect of clonal interference is reduced over time since stronger mutations are less likely to be interfered by other mutations (Equation 10). This would lead to a speed-up of the form of the trajectory if the population started off in the clonal interference regime. Nevertheless, if ${\mu }_d(F)\alpha (F)<1$ (i.e. the deleterious mutation rate is smaller than the mean selection coefficient of beneficial mutations) throughout the measured trajectory, the influence of deleterious mutations is small and our main conclusions would still hold. Experiments with different values of mutation rates would therefore allow one to disentangle the effects of weak deleterious mutations from that of clonal interference.

In the regime where the time taken for a mutant to fix is at least comparable to the time for new successful mutations to emerge, besides interference from other beneficial mutations that emerge in the resident population, the original mutant population can also gain additional mutations. The fixation probabilities of these new mutations are enhanced since they are accumulated in cells that already have a fitness advantage in the population. This effect could be important when there are a large number of different subgroups (i.e. genotypes) in the population, such that the average fixation probability of a mutation (of a certain fitness effect) should also be an average over the different background fitness values the mutation can occur in (Good et al. 2012). In general, not accounting for multiple mutations would underestimate the fixation probabilities of small effect mutations since these benefit most from hitch-hiking (Fogle et al. 2008). However, these small effect mutations also contribute the least amount to fitness, which may explain why taking into account clonal interference alone seems to provide a good agreement with simulated fitness trajectories (Figs. 2 and A2), even when there are more accumulated mutations than predicted by the current framework (Fig. A4). Nevertheless, how including the effect of multiple mutations would affect the functional form of long-term fitness trajectories in the presence of epistasis, and how our results extend to the regime of strong clonal interference, are interesting questions that we leave for future work. Another potential direction for future studies is to take into account the interactions between clonal interference and horizontal gene transfer (Slomka et al. 2020) (and how these would affect adaptation dynamics), an aspect we have not studied in this paper.

Data availability

The MATLAB codes for simulation and analysis can be found on GitHub repository https://github.com/yipeiguo/Effect-of-clonal-interference-on-fitness-trajectories.

 

Appendix A: Fixation probability of a new mutant in a population with 2 subgroups

We consider the scenario where there are two genotypes 1 and 2 with growth rates g₁ and g₂ when a new mutant with growth rate g_m emerges. Let ${\tilde{p}}_{\mathit{ext}}[N_1,N_2]$ be the extinction probability of the mutant lineage when there are N₁ type 1 cells and N₂ type 2 cells in the population of constant size N. Assuming the dynamics follow a Moran process, and that no further mutations occur, these extinction probabilities satisfy the following set of equations:

$${\tilde{p}}_{\mathit{ext}}[N_1,N_2]\tilde{R}(N_1,N_2)=\underset{\text{type} 1 \text{replaces type} 2 \left(\text{or vice versa}\right)}{\underbrace{\frac{N_1{N}_2}{N}(g_1{\tilde{p}}_{\mathit{ext}}[N_1+1,N_2-1]+g_2{\tilde{p}}_{\mathit{ext}}[N_1-1,N_2+1])}}$$

$$+\underset{\text{type} 1/2 \text{replaces mutant}}{\underbrace{\frac{N-N_1-N_2}{N}(g_1{N}_1{\tilde{p}}_{\mathit{ext}}[N_1+1,N_2]+g_2{N}_2{\tilde{p}}_{\mathit{ext}}[N_1,N_2+1])}}$$

$$+\underset{\text{mutant replaces type} 1/2}{\underbrace{\frac{(N-N_1-N_2)g_m}{N}(N_1{\tilde{p}}_{\mathit{ext}}[N_1-1,N_2]+N_2{\tilde{p}}_{\mathit{ext}}[N_1,N_2-1])}}$$

$$+\underset{\text{no change}}{\underbrace{\frac{1}{N}\left(N_1^{\mathrm{2}}{g}_1+N_2^{\mathrm{2}}{g}_2+{(N-N_1-N_2)}^2{g}_m\right){\tilde{p}}_{\mathit{ext}}[N_1,N_2]}},$$ (A1)

where the first term on the right takes into account the probability that the next event involves the division of a type 1 cell and the removal of a type 2 and vice versa, the second term involves the removal of the mutant, the third term is associated with the division of the mutant and removal of one of the other cell types, and the last term is for cases where there is no change in the composition of the population. The boundary conditions are ${\tilde{p}}_{\mathit{ext}}[0,0]=0$ and ${\tilde{p}}_{\mathit{ext}}[N_1,N_2]=1$ when $N_1+N_2=N$, and $\tilde{R}(N_1,N_2)$ is the total growth rate of all cells:

$$\tilde{R}(N_1,N_2)=N_1{g}_1+N_2{g}_2+(N-N_1-N_2)g_m.$$ (A2)

The corresponding fixation probabilities ${\tilde{p}}_f[N_1,N_2]=1-{\tilde{p}}_{\mathit{ext}}[N_1,N_2]$ can then be obtained exactly by solving this large system of $\frac{N(N+1)}{2}-1$ linear equations (Equation A1).

The extinction probability $p_{\mathit{ext}}[n]$ of a newly emerged mutant cell is then given by:

$$p_{\mathit{ext}}[n]={\tilde{p}}_{\mathit{ext}}[n(N-1),(1-n)(N-1)],$$ (A3)

where n is the fraction of type 1 cells among the type 1 and 2 cells.

Since $N_1=n(N-1)$ and $N_2=(1-n)(N-1)$, for $N\gg 1$,

$${\tilde{p}}_{\mathit{ext}}[N_1+1,N_2-1]=p_{\mathit{ext}}\left[n+\frac{1}{N-1}\right]\approx p_{\mathit{ext}}\left[n+\frac{1}{N}\right],$$ (A4)

$${\tilde{p}}_{\mathit{ext}}[N_1-1,N_2+1]=p_{\mathit{ext}}\left[n-\frac{1}{N-1}\right]\approx p_{\mathit{ext}}\left[n-\frac{1}{N}\right],$$ (A5)

$${\tilde{p}}_{\mathit{ext}}[N_1+1,N_2]={\tilde{p}}_{\mathit{ext}}[N_1,N_2+1]=1.$$ (A6)

If there are two mutant cells in the population, the probability of the mutant strain eventually going extinct is the probability that the lineages of both mutant cells separately go extinct. In the large N limit, the fates of the two mutant cells can be assumed to be approximately independent of one another, such that:

$${\tilde{p}}_{\mathit{ext}}[N_1-1,N_2]={\left(p_{\mathit{ext}}\left[\frac{n(N-1)-1}{N-2}\right]\right)}^2\approx {\left(p_{\mathit{ext}}\left[n-\frac{1-n}{N-1}\right]\right)}^2,$$ (A7)

$${\tilde{p}}_{\mathit{ext}}[N_1,N_2-1]={\left(p_{\mathit{ext}}\left[\frac{n(N-1)}{N-2}\right]\right)}^2\approx {\left(p_{\mathit{ext}}\left[n+\frac{n}{N-1}\right]\right)}^2.$$ (A8)

Substituting these expressions (Equations A4–A8) into Equation (A1) and allowing terms of O(1) and above in N (which is why we neglect the change in n when the mutant replaces a type 1/2 cell—this requires the mutant to divide and the probability of the mutant being the next to divide is a factor of N lower than a type 1/2 cell being the next to divide), $p_{\mathit{ext}}[n]$ satisfies the following equation:

$$p_{\mathit{ext}}[n]R(n)=\underset{\text{type} 1 \text{replaces type} 2 \left(\text{or vice versa}\right)}{\underbrace{\frac{{(N-1)}^2}{N}n(1-n)\left(g_1{p}_{\mathit{ext}}\left[n+\frac{1}{N}\right]+g_2{p}_{\mathit{ext}}\left[n-\frac{1}{N}\right]\right)}}$$

$$+\underset{\text{mutant removed}}{\underbrace{\frac{N-1}{N}(g_{1}n+g_2(1-n))}}+\underset{\text{mutant replaces type} 1/2}{\underbrace{\frac{N-1}{N}{g}_m{p}_{\mathit{ext}}^2[n]}}$$

$$+\underset{\text{no change}}{\underbrace{\left(\frac{{(N-1)}^2}{N}(n^2{g}_1+{(1-n)}^2{g}_2)+\frac{g_m}{N}\right)p_{\mathit{ext}}\left[n\right]}},$$ (A9)

with $R(n)=(N-1)(n{g}_1+(1-n)g_2)+g_m$ (from Equation A2).

For $N\gg 1$,

$$p_{\mathit{ext}}\left[n+\frac{1}{N}\right]\approx p_{\mathit{ext}}[n]+\frac{1}{N}p{\prime }_{\mathit{ext}}\left[n+\frac{1}{2N}\right],$$ (A10)

$$p_{\mathit{ext}}\left[n-\frac{1}{N}\right]\approx p_{\mathit{ext}}[n]-\frac{1}{N}p{\prime }_{\mathit{ext}}\left[n-\frac{1}{2N}\right],$$ (A11)

such that

$$\begin{array}{c}{g}_1{p}_{\mathit{ext}}\left[n+\frac{1}{N}\right]+g_2{p}_{\mathit{ext}}\left[n-\frac{1}{N}\right]\hfill \\ =(g_1+g_2)p_{\mathit{ext}}[n]+\frac{1}{N}\left(g_{1}p{\prime }_{\mathit{ext}}\left[n+\frac{1}{2N}\right]-g_{2}p{\prime }_{\mathit{ext}}\left[n-\frac{1}{2N}\right]\right)\hfill \\ =(g_1+g_2)p_{\mathit{ext}}[n]+\frac{1}{N}\left(\left(\frac{\omega +\Omega }{2}\right)p{\prime }_{\mathit{ext}}\left[n+\frac{1}{2N}\right]-\left(\frac{\omega -\Omega }{2}\right)p{\prime }_{\mathit{ext}}\left[n-\frac{1}{2N}\right]\right),\hfill \\ \text{where} \omega =g_1+g_2 \text{and} \Omega =g_1-g_2\\ =(g_1+g_2)p_{\mathit{ext}}[n]+\frac{\omega }{2N^2}p\prime {\prime }_{\mathit{ext}}[n]+\frac{\Omega }{N}p{\prime }_{\mathit{ext}}[n].\hfill \end{array}$$ (A12)

Substituting this into Equation (A9), letting $g_2=g_1(1+s)>g_1$ and $g_m=g_1(1+s_I)>g_1$, and taking the large N limit, the solution for $p_f(n)=1-p_{\mathit{ext}}[n]$ is given by:

$$\underset{1}{\underbrace{(1+s_I)p_f^2(n)}}+\underset{2}{\underbrace{(s(1-n)-s_I)p_f(n)}}-\underset{3}{\underbrace{\frac{D(n)}{2}\frac{{\partial }^2{p}_f(n)}{{\partial }^{2}n}}}+\underset{4}{\underbrace{v(n)\frac{\partial p_f(n)}{\partial n}}}=0,$$ (A13)

where $D(n)=\frac{n(1-n)}{N}(2+s),\hspace{0.17em}v(n)=n(1-n)s$, and the boundary conditions are given by $p_f(0)=(s_I-s)/(1+s_I)$ and $p_f(1)=s_I/(1+s_I)$. In the large N limit, the third term will be much smaller than the other terms.

If the first two terms in Equation (A13) dominate (either when n is close to 0 or 1, or when $s_I\gg s$),

$$\begin{array}{c}{p}_f(n)\approx p_f^{*}(n)=\frac{s_I-s(1-n)}{1+s_I}\hfill \\ \approx s_I-s(1-n),\hfill \end{array}$$ (A14)

where in the second line we have taken the limit $s_I\ll 1$. For $0<n<1$ and s > 0, the fourth term in Equation (A13) is positive and hence this expression is an overestimate of the true fixation probability.

Denoting the actual fixation probability as:

$$p_f(n)=p_f^{*}(n)+\Delta (n)$$ (A15)

and substituting this back into Equation (A13), we find that to first order in Δ and in the limit $s_I\ll 1,\hspace{0.17em}\Delta (n)$ satisfies the following equation:

$$\frac{\partial \Delta }{\partial n}+\frac{s_I-s(1-n)}{n(1-n)s}\Delta +s=0.$$ (A16)

Defining the integrating factor:

$$I(n)=e^{{\int }_0^n\frac{s_I-s(1-\tilde{n})}{\tilde{n}(1-\tilde{n})s}d\tilde{n}}=\frac{n^{\frac{\delta s}{s}}}{{(1-n)}^{1+\frac{\delta s}{s}}}$$ (A17)

with $\delta s=s_I-s$, the solution to Equation (A16) is given by:

$$\Delta (n,s,\delta s)=-s\frac{{\int }_0^{n}I(\tilde{n},\frac{\delta s}{s})d\tilde{n}}{I(n,\frac{\delta s}{s})}$$ (A18)

which satisfies the boundary conditions $\Delta (n=0)=\Delta (n=1)=0$.

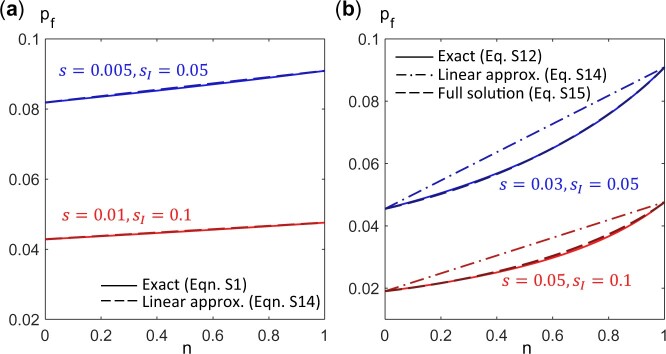
We find that these expressions for the fixation probability provide a good estimate of the exact values for a finite (but large) population (Fig. A1).

Fig. A1.

Fixation probability p_f of a mutant (with growth rate $g_m=1+s_I$) as a function of n, the fraction of type 1 cells in a population of size N = 1,000. Type 1 cells have growth rate $g_1=1$ and type 2 cells have growth rate $g_2=1+s$. a) When $s\ll s_I$ (blue curves: s = 0.005, $s_I=0.05$, red curves: s = 0.01, $s_I=0.1$), $p_f(n)$ is approximately linear in n and is given by the selective advantage of the mutant over that of the population average. Solid lines are exact solutions obtained from Equation (A1) while dashed lines plot the expression in Equation (A14). b) In general, $p_f(n)$ is not a linear function of n (dash-dotted lines, Equation A14), but is well approximated by Equations (A15) and (A18) (dashed lines vs solid lines). [Blue curves: s = 0.03, $s_I=0.05$, red curves: s = 0.05, $s_I=0.1$.]

Appendix B: Effect of clonal interference on fitness trajectories

The rate that a successful interfering mutation emerges at generation t after a mutation of fitness effect s has escaped loss via genetic drift and is still on its way to taking over the population is given by:

$$R_I(t)=N{\mu }_{b0}n(t){\int }_s^{\infty }\rho (s_I|F)p_f(n(t)|s,s_I)d{s}_I,$$ (A19)

where $n(t)=\frac{(N-1)e^{-st}}{1+(N-1)e^{-st}}$ is the fraction of resident cells at generation t (assuming deterministic, logistic growth of the mutant strain), $p_f(n(t)|s,s_I)$ is the fixation probability of the interfering mutant with fitness effect s_I (Appendix A), and $\rho (s_I|F)$ is the distribution of fitness effects of beneficial mutations that can arise in a cell with fitness F.

Here, we consider a general class of exponential-like fitness effect distributions that has been adopted in previous theoretical studies (Fogle et al. 2008; Schiffels et al. 2011; Good et al. 2012):

$$\rho (s|F)=\frac{\alpha (F)}{\Gamma (1+1/\beta )}{e}^{-{(\alpha (F)s)}^{\beta }}{e}^{-h(F)}$$ (A20)

where Γ is the Gamma function, $e^{-h}$ is the fraction of mutations that are beneficial, and α and β characterize the shape of the distribution. In particular, if β = 1, we recover the exponential distribution used in the main text (Equation 2). When $\beta >1,\hspace{0.17em}\rho (s)$ falls faster than exponentially; when $\beta <1,\hspace{0.17em}\rho (s)$ falls more slowly than exponentially. The effect of the shape of $\rho (s)$ on the speed of adaptation in the clonal interference regime has been explored in Park et al. (2010) and Fogle et al. (2008) assuming that $\rho (s)$ does not change over time (i.e. no epistasis); here we are interested in how different types of macroscopic epistasis affect the shape of the average fitness trajectory.

Substituting this distribution into Equation (A19) gives:

$$\begin{array}{c}{R}_I(t)=N{\mu }_{b0}{e}^{-h(F)}n(t){{\displaystyle \int }}_0^{\infty }\frac{\alpha (F)}{\Gamma (1+1/\beta )}{e}^{-{(\alpha (F)(s+\delta s))}^{\beta }}{p}_f(n(t),s,\delta s)d\delta s\hfill \\ =\frac{N{\mu }_{b0}{e}^{-h(F)}n(t)}{\alpha (F)}f(\tilde{s},n(t)),\hfill \end{array}$$ (A21)

where $\tilde{s}=\alpha (F)s,\hspace{0.17em}\delta s=s_I-s$, and the function $f(\tilde{s},n(t))$ depends on the value of β and whether we adopt the approximate (linear in n, Equation A14) or more accurate (Equations A15 and A18) expression for $p_f(n(t),s,\delta s)$. For β = 1, if we assume that $p_f(n(t),s,\delta s)=\delta s+sn(t)$ (Equation A14), then $f(\tilde{s},n(t))=e^{-\tilde{s}}(1+\tilde{s}n(t))$.

Integrating this over all possible times the interfering mutant can emerge gives:

$$\begin{array}{c}\lambda (\tilde{s},F)={\int }_0^T{R}_I(t)dt=\frac{N{\mu }_{b0}{e}^{-h(F)}}{\alpha (F)}{\int }_0^{\frac{2}{s}\text{log}(N-1)}n(t)f(\tilde{s},n(t))dt\hfill \\ =\frac{N{\mu }_{b0}{e}^{-h(F)}}{\tilde{s}}{\int }_{1/N}^{1-1/N}\frac{f(\tilde{s},n)}{1-n}dn\hfill \\ =\frac{N{\mu }_{b0}{e}^{-h(F)}}{\tilde{s}}{f}_2(\tilde{s}),\hfill \end{array}$$ (A22)

where $f_2(\tilde{s})$ is a function of $\tilde{s}$. In the main text, we assumed the simple form of $p_f(n(t),s,\delta s)=\delta s+sn(t)$ and β = 1, in which case $f(\tilde{s},n(t))=e^{-\tilde{s}}(1+\tilde{s}n(t))$ and hence:

$$\begin{array}{c}{f}_2(\tilde{s})=e^{-\tilde{s}}\left(\text{log}(N-1)(1+\tilde{s})-\tilde{s}\left(1-\frac{2}{N}\right)\right)\hfill \\ \approx e^{-\tilde{s}}\hspace{0.17em}\text{log}(N)(1+\tilde{s}),\hfill \end{array}$$ (A23)

where we have taken the large N limit ($\text{log}(N)\gg 1$) in the approximation. Substituting this into Equation (A22), we recover Equation (10) in the main text.

Since the fixation probability P_f is reduced by a factor of $e^{-\lambda (\tilde{s},F)}$ in the presence of clonal interference (Equation 5), the dynamics of average fitness is given by:

$$\frac{d\hspace{0.17em}\text{log}(F)}{dt}=\frac{NF{\mu }_{b0}{e}^{-h(F)}}{{\alpha }^2(F)\Gamma (1+1/\beta )}{\int }_0^{\infty }{\tilde{s}}^2{e}^{-({\tilde{s}}^{\beta }+\lambda (\tilde{s},F))}d\tilde{s}.$$ (A24)

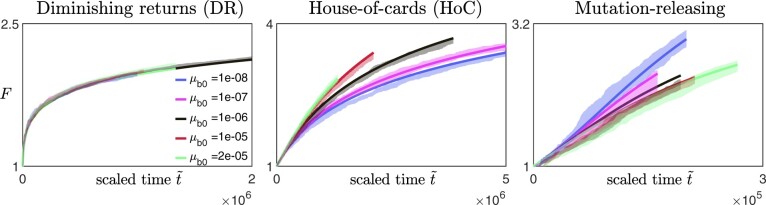
We find that this expression agrees well with the simulation data over a reasonably wide range of mutation rates (with $N{\mu }_{b0}$ not too large, Fig. A2).

Fig. A2.

Scaled fitness trajectories for different values of initial beneficial mutation rates ${\mu }_{b0}$ on different fitness landscapes (left panel: diminishing returns model with $\alpha (F)=20F^5$ and ${\mu }_b={\mu }_{b0}$, middle panel: House-of-Cards/uncorrelated landscape with $\alpha (F)=100F$ and ${\mu }_b={\mu }_{b0}{e}^{-(F-1)}$, right panel: a mutation-releasing landscape with $\alpha (F)=50e^{F-1},\hspace{0.17em}{\mu }_b={\mu }_{b0}{e}^{F-1}$) [Other parameters: $N={10}^6$, β = 1.]. The solid lines are obtained from solving Equation (A24), while the lighter, shaded regions represent the 95%-confidence interval around the mean obtained from the average of 10 simulation replicates. For the case where ${\mu }_{b0}=1\times {10}^{-8}$, we set the rescaled time $\tilde{t}$ to be the actual time t, and for other values of ${\mu }_{b0}$, time is rescaled such that the initial gradient $\frac{dF}{d\tilde{t}}{|}_{t=0}$ is the same as when ${\mu }_{b0}=1\times {10}^{-8}$.

The fact that $\lambda (\tilde{s},F)$ explicitly depends on h(F) but not $\alpha (F)$ implies that only h(F) affects the functional form of the fitness trajectory.

Appendix C: Numerical results with other distributions of fitness effects

We find that our expression for the dynamics of fitness in the clonal interference regime (Equation A24) agrees well with simulation data for other distribution of fitness effects specified through different values of β (Equation A20), and that the conclusion that depletion in beneficial mutations speeds up the functional form of the trajectory holds for these different distributions (Fig. A3).

Fig. A3.

Fitness trajectories on the HoC/uncorrelated landscape with fitness effect distribution $\rho (s)$ specified by a) $\beta =0.5$, b) β  =  1, and c) β  =  2. The parameter β characterizes how fast $\rho (s)$ decays with s (Equation A20). In each sub-figure, the upper panel shows the fitness trajectories as a function of actual time with (red) and without (blue) clonal interference (CI). The solid lines are are obtained from solving Equation (A24) [with λ given by Equation (A22) in the CI regime and λ  =  0 in the SSWM regime], while the dashed lines are individual replicates from simulations. The lower panel compares trajectories (blue and red solid lines in the upper panel) after rescaling time $\tilde{t}=t·A/2$ for the case with clonal interference such that both trajectories have the same derivative at t = 0. [Landscape parameters: $\alpha (F)=100\frac{\Gamma (2/\beta )}{\Gamma (1/\beta )}F,\hspace{0.17em}{\mu }_b={\mu }_{b0}{e}^{-(F-1)}$, other parameters: $N={10}^6,\hspace{0.17em}{\mu }_{b0}=1·{10}^{-5}$.]

Appendix D: Simulation Details

We carry out full simulations of the evolutionary process within the Moran model using the Gillespie algorithm. For each simulation, the population is initialized with N cells, each with initial fitness (i.e. division rate) of 1. Throughout the simulation, we keep track of the size N_i (i.e. number of cells) and fitness F_i of cells in each subgroup $i=1,2,\dots ,n_s$, where n_s is the number of currently existing subgroups that is present in the population. For example, the initial population consists only of n_s = 1 subgroup of size $N_1=N$ and fitness value $F_1=1$. At each point during the simulation, we also calculate the corresponding beneficial mutation rates (i.e. probability of gaining a beneficial mutation per division) ${\mu }_{b,i}(F_i)={\mu }_{b0}{e}^{-h(F_i)}$ (Equation 2, Equation A20) of each subgroup. The possible events that change the composition of the population are: (1) a cell from a subgroup i divides (without mutation) and replaces a cell in another subgroup $j\ne i$, which occurs with rate $R_{i,j}=\frac{N_j}{N}{N}_i{F}_i(1-{\mu }_{b,i})$, and (2) a cell from a subgroup i divides and mutates while a cell from subgroup j is removed, which occurs with rate ${\tilde{R}}_{i,j}=\frac{N_j}{N}{N}_i{F}_i{\mu }_{b,i}$. The total rate of an event occurring is then given by $R_{\mathit{tot}}=\sum _{i\ne j}{R}_{i,j}+\sum _{i,j}{\tilde{R}}_{i,j}$, and we draw the time to the next event from an exponential distribution with mean given by $1/R_{\mathit{tot}}$. The next event is drawn with probability proportional to the rate at which the event occurs, and the composition of the population is updated accordingly. If a beneficial mutation occurs while a cell in subgroup i divides (i.e. event type b), we draw its selection coefficient from the specified distribution with mean given by $\langle s\rangle (F_i)=\frac{\Gamma (2/\beta )}{\Gamma (1/\beta )}\frac{1}{\alpha (F_i)}$ (Equation A20, or Equation [2] if β  =  1), and this new mutant is stored as a new subgroup.

Appendix E: Effect of clonal interference on substitution trajectories

Analogous to the fitness trajectory, the average substitution trajectory S(t) (i.e. the number of fixed mutations as a function of time) is given by:

$$\frac{dS}{dt}=NF{\mu }_{b0}{\int }_0^{\infty }{P}_f(s)\rho (s|F)ds.$$ (A25)

Assuming an exponential distribution of fitness effects (Equation 2), in the SSWM regime, the average substitution trajectory is therefore given by:

$$\frac{dS}{dt}=\frac{NF{\mu }_{b0}{e}^{-h(F)}}{\alpha (F)}=\frac{\alpha (F)}{2}\frac{d\hspace{0.17em}\text{log}(F)}{dt}.$$ (A26)

In the presence of weak clonal interference, assuming the simplified linear expression for the fixation probability (Equation A14) gives:

$$\frac{dS}{dt}=\frac{NF{\mu }_{b0}{e}^{-h(F)}}{\alpha (F)}{\int }_0^{\infty }\tilde{s}{e}^{-(\tilde{s}+\lambda (\tilde{s},F))}d\tilde{s},$$ (A27)

where $\lambda (\tilde{s},F)$ is the same as in the expression for fitness dynamics (Equation 10).

As for the fitness trajectory, Equations (A26) and (A27) suggest that clonal interference changes the form of the substitution trajectory only through h(F). If the beneficial mutation rate μ_b stays the same, the form of the substitution trajectory stays the same regardless of whether there is clonal interference. If μ_b decreases with fitness, the form of the substitution trajectory speeds up; if instead μ_b increases, the trajectory slows down.

When comparing the numerical solutions of Equation (A27) across different values of ${\mu }_{b0}$, we first scale time as we would for the fitness trajectories (such that the initial fitness gradient $\frac{dF}{d\tilde{t}}{|}_{t=0}$ is the same) and then scale S accordingly such that $\frac{d{\tilde{S}}_{\text{CI}}}{d\tilde{t}}{|}_{t=0}$ is the same. For small values of $N{\mu }_{b0}$ (see lines for ${\mu }_{b0}={10}^{-8}$ and ${\mu }_{b0}={10}^{-7}$ in Fig. A4), Equation (A27) agrees well with the simulation data and we see indeed that as ${\mu }_{b0}$ is increased from ${10}^{-8}$ to ${10}^{-7}$, the shape of the trajectory remains unchanged in the diminishing-returns model, speeds up in the HOC landscape, and slows down in a mutation-releasing landscape.

Fig. A4.

Scaled substitution trajectories $\tilde{S}$ for different values of initial beneficial mutation rates ${\mu }_{b0}$ on different fitness landscapes (left panel: diminishing returns model with $\alpha (F)=20F^5$ and ${\mu }_b={\mu }_{b0}$, middle panel: House-of-Cards/uncorrelated landscape with $\alpha (F)=100F$ and ${\mu }_b={\mu }_{b0}{e}^{-(F-1)}$, right panel: a mutation-releasing landscape with $\alpha (F)=50e^{F-1},\hspace{0.17em}{\mu }_b={\mu }_{b0}{e}^{F-1}$) [Other parameters: $N={10}^6$, β = 1]. The solid lines are obtained from solving Equation (A27), while the lighter, shaded regions represent the 95%-confidence interval around the mean obtained from the average of 10 simulation replicates. The rescaled time $\tilde{t}$ is the same as that for the fitness trajectories in Fig. A2. The average number of accumulated mutations S is not scaled for the case where ${\mu }_{b0}=1\times {10}^{-8}$, and for the other values of ${\mu }_{b0}$, S is rescaled such that the initial gradient $\frac{d\tilde{S}}{d\tilde{t}}{|}_{t=0}$ is the same as when ${\mu }_{b0}=1\times {10}^{-8}$.

However, as the value of ${\mu }_{b0}$ is increased further, Equation (A27) increasingly underestimates the mutation trajectory. This is the case even though the fitness trajectories are in good agreement with the theory (Fig. A2), suggesting that the excess mutations observed in the simulations likely arise from nearly neutral mutations that do not contribute much to fitness. The fixation of nearly neutral mutations that typically do not fix on their own could occur, for example, when a neutral mutant gains an additional beneficial mutation which then drives fixation. Therefore, to distinguish the different types of macroscopic epistasis (and in particular whether μ_b changes over time), comparing the shape of fitness trajectories would be more reliable (i.e. would work over a larger range of $N\mu$) than comparing substitution trajectories.

Appendix F: Effect of varying Fc when estimating initial gradient

In practice, experimental data consist of fitness values measured at discrete time points. One way of estimating the initial gradient of the fitness trajectory is to find the time point t_c when the average fitness $F(t_c)$ first exceeds some value F_c, and let the estimate $\widehat{F_0^{\prime }}$ of the initial slope be $\frac{F(t_c)-1}{t_c}$. When comparing the shape of fitness trajectories across different values of N, the time for each trajectory is rescaled ($\tilde{t}=kt$), with the scaling factor k being proportional to the corresponding value of $\widehat{F_0^{\prime }}$. By solving Equation (9) for different landscapes and then rescaling the trajectories using different estimates of gradients using different values of F_c, we find that our qualitative results are insensitive to the choice of F_c (Fig. A5).

Fig. A5.

The effect of varying F_c when estimating initial fitness gradient on scaled fitness trajectories. The trajectories are obtained from solving Equation (9), with the rescaled time $\tilde{t}=kt$, where k is the estimated initial gradient over that for the case with N = 1,000. Top row: diminishing returns model with $\alpha (F)=20F^5$ and ${\mu }_b={\mu }_{b0}$, middle row: House-of-Cards/uncorrelated landscape with $\alpha (F)=100F$ and ${\mu }_b={\mu }_{b0}{e}^{-(F-1)}$, bottom row: a mutation-releasing landscape with $\alpha (F)=50e^{F-1},\hspace{0.17em}{\mu }_b={\mu }_{b0}{e}^{F-1}$. [Other parameters: ${\mu }_b=1\times {10}^{-5}$.]