Crystal growth engineering and origin of the weak ferromagnetism in antiferromagnetic matrix of orthochromates from t-e orbital hybridization

Summary

We report a combined experimental and theoretical study on intriguing magnetic properties of quasiferroelectric orthochromates. Large single crystals of the family of RECrO₃ (RE = Y, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, and Lu) compounds were successfully grown. Neutron Laue study indicates a good quality of the obtained single crystals. Applied magnetic field and temperature dependent magnetization measurements reveal their intrinsic magnetic properties, especially the antiferromagnetic (AFM) transition temperatures. Density functional theory studies of the electronic structures were carried out using the Perdew-Burke-Ernzerhof functional plus Hubbard U method. Crystallographic information and magnetism were theoretically optimized systematically. When RE³⁺ cations vary from Y³⁺ and Eu³⁺ to Lu³⁺ ions, the calculated t-e orbital hybridization degree and Néel temperature behave similarly to the experimentally determined AFM transition temperature with variation in cationic radius. We found that the t-e hybridization is anisotropic, causing a magnetic anisotropy of Cr³⁺ sublattices. This was evaluated with the nearest-neighbor J₁-J₂ model. Our research provides a picture of the electronic structures during the t-e hybridization process while changing RE ions and sheds light on the nature of the weak ferromagnetism coexisting with predominated antiferromagnetism. The available large RECrO₃ single crystals build a platform for further studies of orthochromates.

Graphical abstract

Highlights

• •The lack of large and good-quality single crystals of orthochromates has been solved
• •Nature of the weak ferromagnetism in a main antiferromagnetic matrix has been revealed
• •t-e orbital hybridization is the microscopic origin
• •Relationship between microscopic and macroscopic properties has been correlated

Crystal engineering; Condensed matter physics; Magnetism

Introduction

Multiferroic materials have received considerable attention because of their potential application in electric and magnetic devices (Fiebig et al., 2016; Huang et al., 2021; Hur et al., 2004; Jones et al., 2014; Spaldin and Ramesh, 2019). Within the materials, long-range orders such as ferroelectric and magnetic coexist and may interact strongly on each other, providing multi-tunable parameters for tailoring the macroscopic functionalities. There are significant challenges for a complete understanding of the microscopic mechanisms underlying their intriguing macroscopic properties.

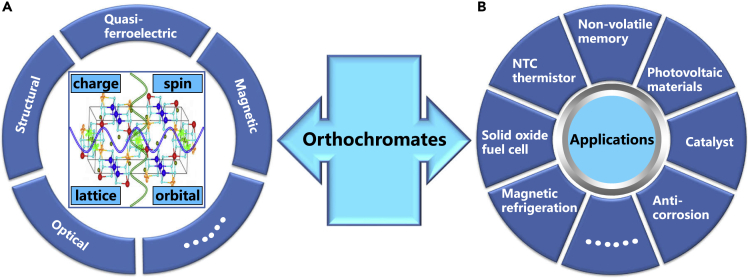
Chromium-based perovskites have attracted considerable interest because of their intriguing magnetic and ferroelectric properties as well as potential technique applications. The set of chromium-based RECrO₃ (RE = rare earths) compounds was suggested to be another family of multiferroic materials, usually displaying ferroelectricity, weak ferromagnetism, and a wide application in fields of catalyst, thermistor, solid-oxide fuel cell, and nonvolatile memory devices (Figure 1) (Oliveira, 2017). The formation of Cr³⁺ magnetic orders has a strong effect on the ferroelectric property, i.e., there may be a magnetoelectric coupling effect (Oliveira et al., 2020; Rajeswaran et al., 2012). Chromium ions in RECrO₃ compounds hold a single-valence state, i.e., ${\text{Cr}}^{3+}\left(t_{2\text{g}}^3{e}_{\text{g}}^0\right)$, naturally discarding the e_g orbital ordering as well as its perturbation on the t_2g electrons. This results in a tightly localized electric environment, an ideal platform for the potential coexistence of ferroelectricity and magnetism. The ferroelectric transition temperature, (T_C ∼ 473 K), of YCrO₃ compound is much higher than that of the antiferromagnetic (AFM) phase transition of Cr³⁺ ions $\left(T_{\text{N}}^{\text{Cr}}\sim 141.5K\right)$ (Serrao et al., 2005; Zhu et al., 2020a). An isosymmetric structural phase transition was observed at ∼ 900 K in a neutron powder diffraction study on the pulverized YCrO₃ single crystal, where the incompressibility of lattice constants a, b, and c is anisotropic, and there exist obvious atomic displacement and charge subduction on the Y and O2 sites (Zhu et al., 2020b). Net electric polarization was observed for polycrystalline LuCrO₃ and ErCrO₃ samples below $T_{\text{N}}^{\text{Cr}}$, indicating the presence of a possible ferroelectric state, whereas this is clearly absent above $T_{\text{N}}^{\text{Cr}}$. Most importantly, the study demonstrates that the paramagnetic (PM) nature of RE sites is not necessary to accommodate the ferroelectricity in orthochromates (Preethi Meher et al., 2014). In addition, the polarizations attain maximum values of ∼ 90 μC/m² (at E = 165 kV/cm for LuCrO₃ compound) and ∼ 70 μC/m² (at E = 174 kV/cm for ErCrO₃ compound). Both polarizations are reversal and can be explained by either the Cr³⁺ off-centering or the ferroelasticity or their couplings and even by Cr³⁺ vacancies (Preethi Meher et al., 2014). The SmCrO₃ compound demonstrates an electric polarization with the maximum value of ∼ 8 μC/m² at E = 1.43 kV/cm and ∼ 15 K (El Amrani et al., 2014), which was ascribed to a breaking of the local symmetry via Cr³⁺ off-centering (El Amrani et al., 2014). It was observed that electric dipoles exist in the DyCrO₃ compound, which was attributed to the displacement of Cr³⁺ cations (Yin et al., 2018). Electric polarizations were observed in TbCrO₃ and TmCrO₃ compounds at E = 1.43 kV/cm below $T_{\text{N}}^{\text{Cr}}$ (Rajeswaran et al., 2012), whereas the existence of electric dipoles in the TmCrO₃ compound remains a debate (Yoshii and Ikeda, 2019).

Figure 1.

Properties and applications of orthochromates

(A) Orthochromates display some interesting properties such as quasiferroelectric, structural, magnetic, and optical, resulting from couplings between charge, spin, orbital, and lattice degrees of freedom.

(B) These make orthochromates potential as magnetic refrigeration, solid oxide fuel cell, negative-temperature-coefficient (NTC) thermistor, nonvolatile memory application, photovoltaic materials, catalyst, and anticorrosion field.

Most previous studies focused on polycrystals, nanocrystals, and thin films. Single crystal growths of rare-earth orthochromates utilize mainly two methods: (i) one is the flux method (Yin et al., 2015). Unfortunately, impurities from the flux exist in the grown single crystals and have strong effects on macroscopic properties of the host (Cooke et al., 1974; Li et al., 2021; Looby and Katz, 1954; Zhu et al., 2020c). In addition, single crystals grown by the flux method are small, normally millimeter in size, and not suitable for some studies that make excessive demands in sample’s quality and mass. (ii) The other is the floating-zone (FZ) method with a mirror furnace. Unfortunately, the intense volatility of Cr element because of its high vapor pressure at melting points of orthochromates (Philipp et al., 2003) can practically reduce the heating power of the mirror furnace (Li, 2008). This makes it not so easy to stably grow the single crystals of orthochromates. As a consequence, the lack of large single crystals has been a long-standing obstacle for studying their intrinsic properties and realizing some potential applications of orthochromates.

One of the long-standing unsolved issues existing in the family of RECrO₃ orthochromates is the microscopic origin of the weak ferromagnetism. This is introduced by the canted AFM structure. The Cr³⁺ state $\left(t_{2\text{g}}^3{e}_{\text{g}}^0\right)$ in orthochromates enables a virtual charge transfer (VCT) of ${\text{Cr}}^{3+}\left(t_{2\text{g}\uparrow }^3\right)-{\text{O}}^{2-}-{\text{Cr}}^{3+}\left(e_{\text{g}}^0\right)$ and a possible ferromagnetic (FM) competition with superexchange interactions J ∼ b²/U (Landron and Lepetit, 2008), where b is the overlapping integral, and U denotes the on-site Coulomb interactions (Slater and Koster, 1954; Zhou et al., 2010). The overall Cr-O-Cr superexchange comprises two major contributions: One is from the $t_{2\text{g}}-t_{2\text{g}}$ hopping, producing an AFM component; the other is from the $t_{2\text{g}}-e_{\text{g}}$ orbital hybridization, generating FM couplings. The hybridization strength depends on the lattice distortion (Siddique et al., 2021), on-site Coulomb interaction (Besbes et al., 2019; Yekta et al., 2021), and $t_{2\text{g}}-e_{\text{g}}$ crystal field splitting (Ko et al., 2007). The spin-orbit coupling induced Dzyaloshinskii-Moriya (DM) exchange would favor a magnetic structure with spins perpendicular to each other to minimize the total energy of the system (Coffey et al., 1991; Dmitrienko et al., 2014). To describe the effect of RE sites on the Cr³⁺-O^2--Cr³⁺ superexchange interactions, one can utilize density functional theory (DFT) based first-principles calculations to optimize the atomic information and correlate it with the superexchange interactions in RECrO₃ compounds. This provides a quantitative description of the t-e hybridization process. In addition, the AFM transition temperatures can be further calculated for a qualitative comparison to those measured from the grown single crystals.

In this paper, we report on a successful single crystal growth of the family of RECrO₃ compounds by a laser-diode FZ technique. Large single crystals measuring centimeters in size were obtained with the largest mass >10 g. The results from in-house characterizations on grown single crystals are in agreement with those from our first-principles calculations. Our research reveals that the t-e hybridization process can be tuned by RE-ions and induce FM interactions in the main AFM matrix and sheds light on the coexistence of weak ferromagnetism with antiferromagnetism and ferroelectricity in orthochromates.

Results

Grown single crystals

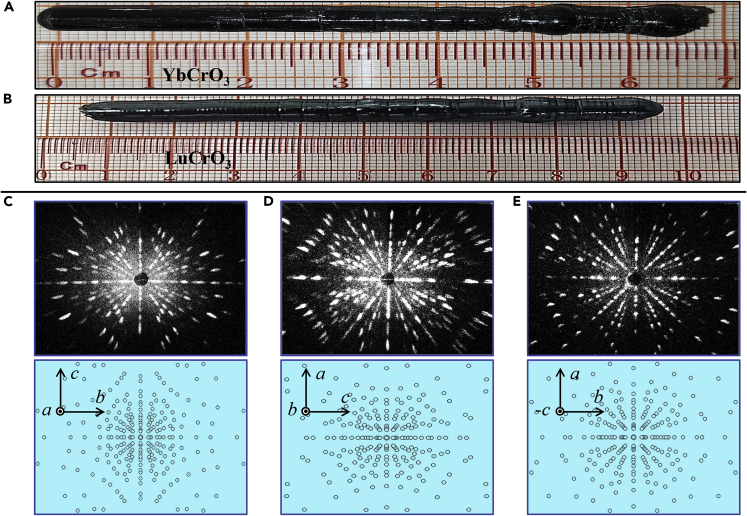
Single-crystal materials hold translational symmetry of long-range building blocks; therefore, they provide reliable information of structures and properties of matters (Cheng, 2017; Li et al., 2018; Sun et al., 2019; Xiong et al., 2021; Zhang, 2020). Exploring and optimizing the single crystal growth parameters are time-consuming and labor-intensive processes (Li, 2008). For the first time, we have grown large single crystals of the family of RECrO₃ (RE = Y, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, and Lu) compounds. Photos of some representative single crystals as-grown are exhibited in Figures 2A and 2B, where the YbCrO₃ (Figure 2A, ∼ 7 cm in length) and LuCrO₃ (Figure 2B, ∼ 10 cm) crystals have a diameter of φ = 6 – 8 mm and very shining surfaces. So far, the largest single crystal of orthochromates we have grown is >10 g for the EuCrO₃ compound. Our crystal growth engineering of RECrO₃ compounds produced a China invention patent (Li et al., 2021).

Figure 2.

As-grown single crystals and neutron Laue diffraction patterns

(A) Photograph of a YbCrO₃ single crystal.

(B) Photograph of a LuCrO₃ single crystal as grown by a laser-diode FZ furnace.

(C–E) Neutron Laue patterns of single-crystal YCrO₃ (top panels) and the corresponding theoretical simulations (bottom panels). The real-space lattice vectors are marked in the bottom panels, and the crystallographic a axis (C), b axis (D), and c axis (E) are perpendicular to the paper.

Neutron Laue diffraction patterns

We investigated the grown single crystals with a neutron Laue diffraction study. The top panels of Figures 2C–2E show the monitored neutron Laue patterns of a YCrO₃ single crystal with the three axes perpendicular to the paper: a axis (Figure 2C), b axis (Figure 2D), and c axis (Figure 2E). All patterns display symmetric and very strong diffraction spots, indicating a good quality of the grown single crystal. As shown in the bottom panels of Figures 2C–2E, we theoretically simulated the three patterns by using the OrientExpress software (Ouladdiaf et al., 2006), which further confirmed the good quality of our single crystals.

Magnetic properties

To clearly show features of dc magnetization in the vicinity of magnetic phase transitions, we present temperature-dependent data in the temperature range of 1.8–200 K. For the whole-temperature data (1.8–400 K), please refer to Figure S1. We measured the zero-field cooling (ZFC) magnetization at zero applied magnetic field, trying to explore the negative magnetization behavior and address whether the observed weak ferromagnetism is spontaneous.

We measured the ZFC magnetization data at 1000 Oe in the temperature range of 250–350 K and calculated the inverse magnetic susceptibility ${\chi }^{-1}=B/M$, which can well fit with the Curie-Weiss (CW) law for a pure paramagnetic (PM) state (Li et al., 2006, 2007, 2009; Zhu et al., 2020b),

$${\chi }^{-1}\left(T\right)=\frac{3k_B\left(T-{\Theta }_{\text{CW}}\right)}{N_A{\mu }_{\text{eff}}^2},$$ (Equation 1)

where k_B= 1.38062 $\times$ 10⁻²³ J/K is the Boltzmann constant, ${\Theta }_{\text{CW}}$ is the PM CW temperature, N_A = 6.022 $\times$ 10²³ mol^–1 is Avogadro’s constant, and ${\mu }_{\text{eff}}$ is the effective PM moment. We fit the data to Equation (1), extracting experimental values of the AFM transition temperature $T_{\text{N}}^{\text{Cr}}$, ${\Theta }_{\text{CW}}$, and ${\mu }_{\text{eff}-\text{meas}}$ of RECrO₃ single crystals. These measured values were listed in Table 1. For the RECrO₃ compounds, it is pointed out that both RE³⁺ and Cr³⁺ ions contribute to the effective PM moment; therefore, the theoretical total effective PM moment ${\mu }_{\text{eff}-\text{theo}}^{\text{total}}=\sqrt{{\left({\mu }_{\text{eff}-\text{theo}}^{\text{RE}}\right)}^2+{\left({\mu }_{\text{eff}-\text{theo}}^{\text{Cr}}\right)}^2}$, where ${\mu }_{\text{eff}-\text{theo}}^{\text{RE}}=g{\mu }_{\text{B}}\sqrt{J\left(J+1\right)}$, and ${\mu }_{\text{eff}-\text{theo}}^{\text{Cr}}=g{\mu }_{\text{B}}\sqrt{S\left(S+1\right)}=3.873{\mu }_{\text{B}}$ (where $S=3/2$). The quantum numbers of RE³⁺ and Cr³⁺ ions and the calculated values of ${\mu }_{\text{eff}-\text{theo}}^{\text{RE}}\text{ and }{\mu }_{\text{eff}-\text{theo}}^{\text{total}}$ were listed in Table 1 for a comparison to the corresponding experimental values. Within 250–350 K, the fits coincide well with the measured magnetization of RECrO₃ (RE = Eu, Tb, Dy, Ho, Er, Tm, Yb, and Lu) single crystals. As temperature decreases from 250 to 220 K, the measured data did not show obvious deviation from the Curie-Weiss law fitting (short-dashed line), which confirms the validity of our theoretical fits and that the RECrO₃ (RE = Eu, Tb, Dy, Ho, Er, Tm, Yb, and Lu) single crystals remain a pure PM state in the temperature range of 220–350 K.

Table 1.

Calculated theoretical quantum numbers of RE³⁺ ions in RECrO₃ single crystals based on the Hund’s rule: number of 4f (4d for Y³⁺ ion) electrons, spin S, orbital L, total angular momentum J, Landé factors g_J, and the ground-state term ${}^{2S+1}L_J$

RECrO3 single crystals grown by the FZ method
RE3+ =	Y3+	Eu3+	Gd3+	Tb3+	Dy3+
4dn ion	0
4fn ions		6	7	8	9
S	0	3	7/2	3	5/2
L	0	3	0	3	5
J	0	0	7/2	6	15/2
$g_J$	–	–	2	1.5	1.33
${}^{2S+1}L_J$	${}^{1}S_0$	${}^{7}F_0$	${}^{8}S_{7/2}$	${}^{7}F_6$	${}^{6}H_{15/2}$
${\mu }_{\text{eff}-\text{meas}}\left({\mu }_{\text{B}}\right)$	3.95	6.44	8.40	10.51	11.35
${\mu }_{\text{eff}-\text{theo}}^{\text{RE}}\left({\mu }_{\text{B}}\right)$	0	0	7.937	9.721	10.646
${\mu }_{\text{eff}-\text{theo}}^{\text{total}}\left({\mu }_{\text{B}}\right)$	3.873	3.873	8.832	10.464	11.328
$M_{\text{meas}}\left({\mu }_{\text{B}}\right)$	∼0.147	0.245 (1)	6.43	6.248 (1)	4.834 (1)
$M_{\text{sat}-\text{theo}}^{\text{RE}}\left({\mu }_{\text{B}}\right)$	0	0	7	9	10
$M_{\text{sat}-\text{theo}}^{\text{total}}\left({\mu }_{\text{B}}\right)$	3	3	7.616	9.487	10.440
TN (K)	141.5 (1)	181.6 (1)	169.3 (1)	157.9 (1)	148.5 (1)
θCW (K)	−433.2 (6)	−450.4 (15)	−20.33 (4)	−53.3 (1)	−56.5 (1)

RE3+ =	Ho3+	Er3+	Tm3+	Yb3+	Lu3+
4fn ion	10	11	12	13	14
S	2	3/2	1	1/2	0
L	6	6	5	3	0
J	8	15/2	6	7/2	0
$g_J$	1.25	1.2	1.167	1.143	–
${}^{2S+1}L_J$	${}^{5}I_8$	${}^{4}I_{15/2}$	${}^{3}H_6$	${}^{2}F_{7/2}$	${}^{1}S_0$
${\mu }_{\text{eff}-\text{meas}}\left({\mu }_{\text{B}}\right)$	11.03	10.20	8.35	5.63	4.98
${\mu }_{\text{eff}-\text{theo}}^{\text{RE}}\left({\mu }_{\text{B}}\right)$	10.607	9.581	7.561	4.536	0
${\mu }_{\text{eff}-\text{theo}}^{\text{total}}\left({\mu }_{\text{B}}\right)$	11.292	10.334	8.495	5.964	3.873
$M_{\text{meas}}\left({\mu }_{\text{B}}\right)$	3.999 (1)	6.385 (1)	2.868 (1)	0.883 (1)	1.197 (1)
$M_{\text{sat}-\text{theo}}^{\text{RE}}\left({\mu }_{\text{B}}\right)$	10	9	7	4	0
$M_{\text{sat}-\text{theo}}^{\text{total}}\left({\mu }_{\text{B}}\right)$	10.440	9.487	7.616	5	3
TN (K)	143.2 (1)	135.4 (1)	125.9 (1)	117.9 (1)	122.3 (1)
θCW (K)	19.6 (1)	−30.0 (1)	−90.6 (4)	−17.4 (1)	−110.4 (2)

We listed values of the measured (meas) (μ_eff-meas) and theoretical (theo) effective PM moments $\left({\mu }_{\text{eff}-\text{theo}}^{\text{Cr}}=g_J{\mu }_{\text{B}}\sqrt{S\left(S+1\right)}=3.873{\mu }_{\text{B}}\left({\text{Cr}}^{3+}:3d^3,J=S=\frac{3}{2},g_J=2\right),{\mu }_{\text{eff}-\text{theo}}^{\text{RE}}=g_J{\mu }_B\sqrt{J\left(J+1\right)},\text{and}{\mu }_{\text{eff}-\text{theo}}^{\text{total}}=\sqrt{{\left({\mu }_{\text{eff}-\text{theo}}^{\text{RE}}\right)}^2+{\left({\mu }_{\text{eff}-\text{theo}}^{\text{Cr}}\right)}^2}\right)$, the measured moment (M_meas per formula at 1.8 K and 14 T), and the theoretical saturation moments $\left(M_{\text{sat}-\text{theo}}^{\text{Cr}}=g_J{\mu }_{\text{B}}S=3{\mu }_B,M_{\text{sat}-\text{theo}}^{\text{RE}}=g_J{\mu }_{\text{B}}J,\text{and}{M}_{\text{sat}-\text{theo}}^{\text{total}}=\sqrt{{\left(M_{\text{sat}-\text{theo}}^{\text{RE}}\right)}^2+{\left(M_{\text{sat}-\text{theo}}^{\text{Cr}}\right)}^2}\right)$. The values of T_N, μ_eff-meas, and CW temperature (θ_CW) were extracted from the M-T measurements by the CW-law fitting. The values of M_meas were extracted from the M-B data. The numbers in parenthesis are the estimated standard deviations of the (next) last significant digit. Some parameters of YCrO₃ (Zhu et al., 2020a) and GdCrO₃ (Zhu et al., 2020c) were referred to in our previous studies.

Magnetic hysteresis loops at the low-field regimes were measured. The isothermal field dependence of magnetization with applied magnetic field from –14 to 14 T was supplemented in Figure S2.

In the following, we present analyses of the magnetic properties of RECrO₃ (RE = Eu, Tb, Dy, Ho, Er, Tm, Yb, and Lu) single crystals one by one.

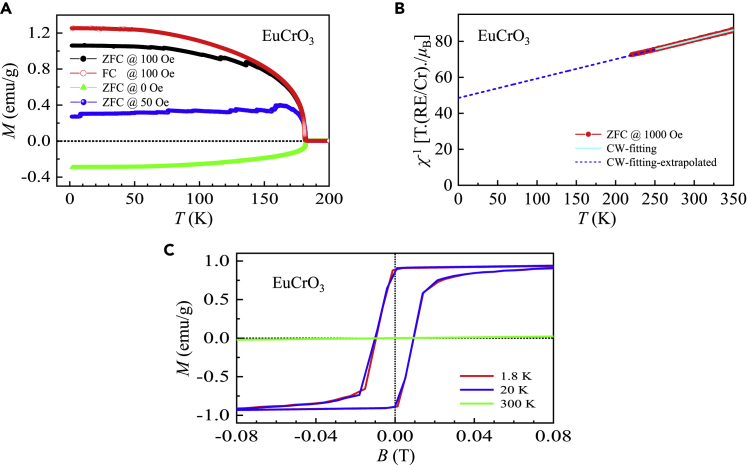
EuCrO₃

EuCrO₃ demonstrates negative magnetization behavior at zero magnetic field below $T_{\text{N}}^{\text{Cr}}$ (Figure 3A), whereas the ZFC magnetization at B = 50 Oe increases sharply below $T_{\text{N}}^{\text{Cr}}$ within a thermal regime of ∼ 1.2 K and then flattens to 1.8 K upon cooling. The field-cooling (FC) magnetization at 100 Oe increases by ∼ 18% at 1.8 K. The magnetization measured at 50 and 100 Oe resembles the features of a weak FM state. We determined that $T_{\text{N}}^{\text{Cr}}=181.6\left(1\right)\text{K}$ for a EuCrO₃ single crystal. Below $T_{\text{N}}^{\text{Cr}}$ EuCrO₃ enters a canted AFM state, probably because of the Dzyaloshinskii-Moriya interactions of Cr³⁺ ions.

Figure 3.

Magnetic property of EuCrO₃

(A) Magnetization as a function of temperature from 1.8–200 K measured at 0, 50, and 100 Oe. We performed both zero-field and field-cooling measurements at 100 Oe.

(B) Zero-field cooling inverse magnetic susceptibility ${\chi }^{-1}$ (solid circles) at an applied magnetic field of 1000 Oe as a function of temperature in the range of 220–350 K. The solid lines represent the fits with a Curie-Weiss law from 250–350 K. The Curie-Weiss law fits were extrapolated to low temperatures shown as short-dashed lines.

(C) Magnetic hysteresis loops measured at low applied magnetic fields with selected temperatures.

To avoid the effect of non-intrinsic magnetic contributions at low applied magnetic fields, we used the ZFC magnetization measured from 250 to 350 K at 1000 Oe for CW fitting (Figure 3B). This produces an effective PM moment ${\mu }_{\text{eff}-\text{meas}}=6.44{\mu }_{\text{B}}$, which is considerably larger than the theoretical value ${\mu }_{\text{eff}-\text{theo}}^{\text{total}}=3.873{\mu }_{\text{B}}$ (Table 1) and a CW temperature ${\Theta }_{\text{CW}}=-450.4\left(15\right)\text{K}$.

The field dependence of magnetization measured at 1.8 K is displayed in Figure 3C, where clear magnetic hysteresis loops are observed at 1.8 and 20 K, and there is nearly no difference between them. Remanent magnetization M_r ∼ 0.91 emu g^–1 and coercive field B_c ∼ 95 Oe were determined. The magnetic hysteresis loop closes at ∼ 867 Oe, after which the ZFC magnetization increases linearly as a function of the magnetic field, with a slope of dM/dB= 0.322(1) emu g^–1 T^–1 (Figure S2A). Given that the theoretical saturation magnetic moment of Cr³⁺ ions is $M_{\text{sat}-\text{theo}}^{\text{Cr}}=g_J{\mu }_{\text{B}}S=3{\mu }_{\text{B}}$, where g_J = 2 and $S=\frac{3}{2}$ for pure ionic Cr³⁺ ions (Table 1), it is inferred that attaining a full magnetic saturation state requires $B\approx 203T$. At 1.8 K and 14 T, a magnetization of M_meas = 0.245 (1) μ_B/Cr was reached (Figure S2A), which is equal to ∼ 8.2% of the theoretical value $M_{\text{sat}-\text{theo}}^{\text{total}}=3{\mu }_{\text{B}}/\text{Cr}$.

Our study indicates a possible existence of competition between FM and AFM exchange interactions. We did not observe the magnetic ordering of Eu³⁺ ions, which is consistent with a previous study on polycrystalline EuCrO₃ samples (Taheri et al., 2016).

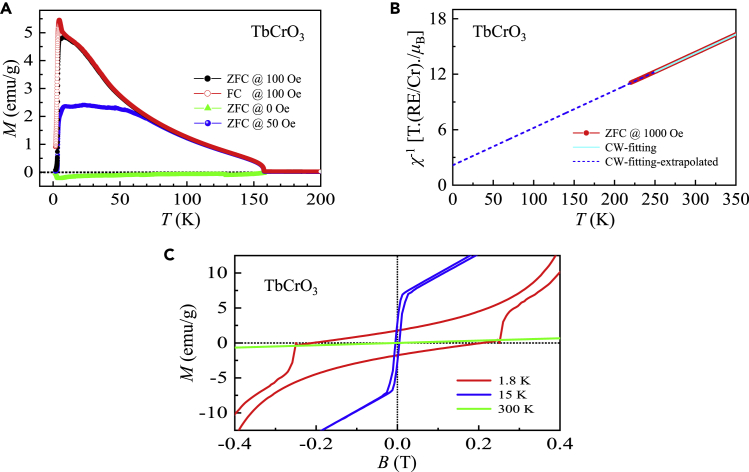
TbCrO₃

We determined that $T_{\text{N}}^{\text{Cr}}=157.9\left(1\right)\text{K}$ for a TbCrO₃ single crystal (Figure 4A). Below $T_{\text{N}}^{\text{Cr}}$, the ZFC magnetization at 0 Oe was negative, whereas the magnetization curves at 50 and 100 Oe increased gradually after a sharp enhancement around $T_{\text{N}}^{\text{Cr}}$ within ∼ 0.56 K. Below ∼ 70 K, the ZFC magnetization at 100 Oe evidently exceeded that measured at 50 Oe. At ∼ 7.7 K, a kink appeared in the magnetization at 50 and 100 Oe (ZFC at 50 and 100 Oe: downturn; FC at 100 Oe: uturn), indicating the formation of Tb³⁺ spin ordering. Below ∼ 4.5 K, a sharp decrease in the magnetization at 50 and 100 Oe and a sharp increase in that at 0 Oe were observed. Below ∼ 3 K, the ZFC magnetization at 0, 50, and 100 Oe approached zero. Therefore, we observe elaborate magnetic phase transitions with temperature in the TbCrO₃ single crystal.

Figure 4.

Magnetic property of TbCrO₃

(A) Magnetization as a function of temperature from 1.8–200 K measured at 0, 50, and 100 Oe. We performed both zero-field and field-cooling measurements at 100 Oe.

(B) Zero-field cooling inverse magnetic susceptibility ${\chi }^{-1}$ (solid circles) at an applied magnetic field of 1000 Oe as a function of temperature in the range of 220–350 K. The solid lines represent the fits with a Curie-Weiss law from 250–350 K. The Curie-Weiss law fits were extrapolated to low temperatures shown as short-dashed lines.

(C) Magnetic hysteresis loops measured at low applied magnetic fields with selected temperatures.

The CW fitting result of μ_eff–meas = 10.51 μ_B (Figure 4B) is nearly equal to the theoretical value ${\mu }_{\text{eff}-\text{theo}}^{\text{total}}=10.464{\mu }_{\text{B}}$. The CW temperature ${\Theta }_{\text{CW}}=-53.3\left(1\right)\text{K}$ indicates a weak competition between the FM and AFM interactions in our TbCrO₃ single crystal.

A clear magnetic hysteresis loop was observed with M_r ∼ 2.75 emu g^–1 and B_c ∼ 48 Oe at 15 K (Figure 4C), indicating a weak FM state of the Cr³⁺ ions. When T = 1.8 K, both Tb³⁺ and Cr³⁺ spins order, and the observed magnetization loop was stretched along the B axis and squeezed along the magnetization axis, leading to a parallelogram-shaped hysteresis loop with M_r ∼ 1.82 emu g^–1 and B_c ∼ 2500 Oe (Figure 4C). Such a twisted loop has not been previously observed in either polycrystalline or single-crystalline (grown by the flux method) samples (Vagadia et al., 2018; Yin et al., 2016). This indicates a stronger coupling between the Cr³⁺ and Tb³⁺ spins in our TbCrO₃ single crystal. As B increased, the loop at 1.8 K gets a quick saturation at B_s ∼ 1.67 T, whereas that at 15 K increased smoothly and attained a plateau at ∼ 6.8 T. At 1.8 K and 14 T, the magnetization reached M_meas = 6.248(1) μ_B, which is ∼ 34% smaller than the theoretical value $M_{\text{sat}-\text{theo}}^{\text{total}}=9.487{\mu }_{\text{B}}$ (Table 1).

TbCrO₃ entered a long-range canted AFM state of Cr³⁺ ions below $T_{\text{N}}^{\text{Cr}}=157.9\left(1\right)$. The possible long-range AFM order of Tb³⁺ ions was formed below $T_{\text{N}}^{\text{Tb}}\sim 7.7\text{K}$. Strong coupling was observed between the spin orders of the Cr³⁺ and Tb³⁺ ions. In addition, a weak competition between the FM and AFM interactions of the Cr³⁺ ions was observed.

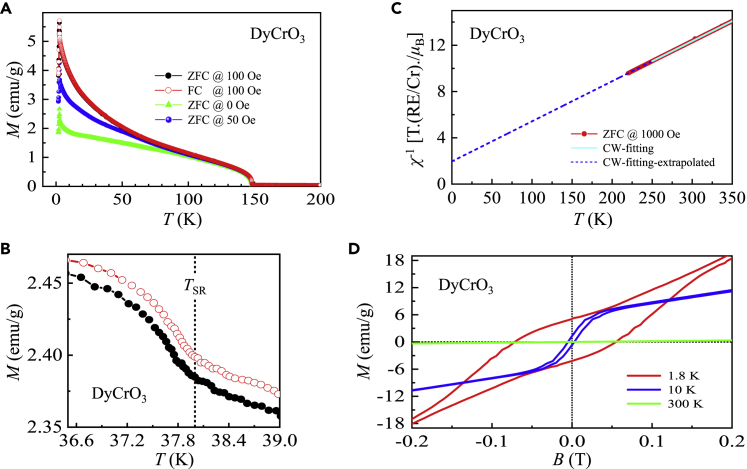
DyCrO₃

The DyCrO₃ single crystal underwent a magnetic phase transition from the PM state to a canted AFM phase at $T_{\text{N}}^{\text{Cr}}=148.5\left(1\right)\text{K}$. (Figure 5A), corresponding to the formation of Cr³⁺ spin ordering. A kink appeared at $T_{\text{SR}}^{\text{Cr}}\sim 38\text{K}$ in the magnetization at 0, 50, and 100 Oe (Figure 5B), which is attributed to the spin reorientation of the Cr ions. A similar observation was previously reported for DyCrO₃ single crystals grown by the flux method, where the appearance of the kink was believed to be caused by the spin reorientation of Dy³⁺ ions (Yin et al., 2016). Below $T_{\text{N}}^{\text{Cr}}$, the magnetization increased smoothly until the onset of a sharp enhancement at ∼ 17 K, reaching a maximum at ∼ 2.54 K and then followed by a quick reduction. Therefore, we observed an AFM phase transition of the Dy³⁺ ions at $T_{\text{N}}^{\text{Dy}}\sim 2.8\text{K}$.

Figure 5.

Magnetic property of DyCrO₃

(A) Magnetization as a function of temperature from 1.8–200 K measured at 0, 50, and 100 Oe. We performed both zero-field and field-cooling measurements at 100 Oe.

(B) Schematically showing the determination of the spin-reorientation temperature T_SR.

(C) Zero-field cooling inverse magnetic susceptibility ${\chi }^{-1}$ (solid circles) at an applied magnetic field of 1000 Oe as a function of temperature in the range of 220–350 K. The solid lines represent the fits with a Curie-Weiss law from 250–350 K. The Curie-Weiss law fits were extrapolated to low temperatures shown as short-dashed lines.

(D) Magnetic hysteresis loops measured at low applied magnetic fields with selected temperatures.

The CW fitting produces μ_eff–meas = 11.35 μ_B (Figure 5C), which is nearly equal to the theoretical value ${\mu }_{\text{eff}-\text{theo}}^{\text{total}}=11.328{\mu }_{\text{B}}$. CW temperature, ${\Theta }_{\text{CW}}=-56.5\left(1\right)\text{K}$ (Table 1).

Isothermal magnetic hysteresis loops were observed at 1.8 (M_r ∼ 4.7 emu g^–1; B_c ∼ 639 Oe) and 10 K (M_r ∼ 1.1 emu g^–1; B_c ∼ 41 Oe) (Figure 5D), confirming that Cr³⁺ spins hold a canted AFM state. For the Dy³⁺ sublattices, we could only conclude that the spins form an AFM state. At both 1.8 and 10 K, the magnetization curves finally flattened with M_meas = 4.834 (1) μ_B at 14 T (Figure S2C). This value was ∼ 53.7% less than the theoretical value of $M_{\text{sat}-\text{theo}}^{\text{total}}=10.440{\mu }_{\text{B}}$ (Table 1).

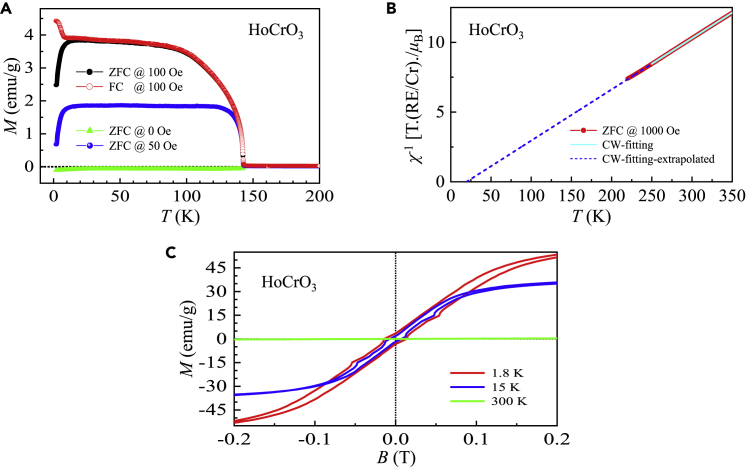
HoCrO₃

We determined that $T_{\text{N}}^{\text{Cr}}=143.2\left(1\right)\text{K}$ for a HoCrO₃ single crystal (Figure 6A). Below $T_{\text{N}}^{\text{Cr}}$, the ZFC magnetization at 0 Oe was negative, whereas those at 50 and 100 Oe were positive and increased smoothly in the temperature regimes of _∼ 19 K (at 50 Oe) and ∼ 47 K (at 100 Oe) and then flatten until $T_{\text{N}}^{\text{Ho}}\sim 7.82\text{K}$, at which Ho³⁺ ions order antiferromagnetically. Below ∼ 2.4 K, all curves were flattened. When $2.4\text{K}<T<T_{\text{N}}^{\text{Ho}}$, the magnetization curves at ZFC (down turn) and FC (up turn) 100 Oe demonstrated an inverse trend; above $T_{\text{N}}^{\text{Ho}}$, they coincided. The degree of canting of the Cr³⁺ AFM structure determines the strength of the resulting ferromagnetism along the c axis. This prevents the formation of an AFM structure of the Ho³⁺ ions. The difference between the ZFC and FC magnetization at 100 Oe is controlled by the competition between the Zeeman energy generated by the applied magnetic field, crystal field, AFM interaction strength of Ho³⁺ ions, and magnetic anisotropy (Li, 2016).

Figure 6.

Magnetic property of HoCrO₃

(A) Magnetization as a function of temperature from 1.8–200 K measured at 0, 50, and 100 Oe. We performed both zero-field and field-cooling measurements at 100 Oe.

(B) Zero-field cooling inverse magnetic susceptibility ${\chi }^{-1}$ (solid circles) at an applied magnetic field of 1000 Oe as a function of temperature in the range of 220–350 K. The solid lines represent the fits with a Curie-Weiss law from 250–350 K. The Curie-Weiss law fits were extrapolated to low temperatures shown as short-dashed lines.

(C) Magnetic hysteresis loops measured at low applied magnetic fields with selected temperatures.

We obtained μ_eff–meas = 11.03 μ_B, which is comparable to ${\mu }_{\text{eff}-\text{theo}}^{\text{total}}=11.292{\mu }_{\text{B}}$, and ${\Theta }_{\text{CW}}=19.6\left(1\right)\text{K}$ (Figure 6B and Table 1). The previous study on polycrystalline HoCrO₃ sample shows μ_eff–meas = 11.55 μ_B and ${\Theta }_{\text{CW}}=-24.0\text{K}$ (Su et al., 2011). Obtaining evidence of short-range exchange interactions and magnetic fluctuations of Ho³⁺ spins reported previously by quasielastic and inelastic neutron scattering studies on HoCrO₃ powder samples (Chatterji et al., 2017; Kumar et al., 2016) necessitates more in-house characterizations with the HoCrO₃ single crystal.

At 1.8 and 15 K, we observed magnetic hysteresis loops in step-increasing mode (Figure 6C). We extracted M_r ∼ 3.5 (1.8 K) and 1.9 (15 K) emu g^–1 and the corresponding B_c ∼ 140 and 72 Oe, respectively. At 15 K, the magnetization increased linearly at B ≤ 618 Oe and then proceeded smoothly into a plateau at ∼ 3.2 T; in contrast, at 1.8 K and B ≤ 1092 Oe, the magnetization almost increased linearly with increasing magnetic field and then attained M_meas = 3.999(1) μ_B at 14 T (Figure S2D). This value was only ∼ 38.3% of the theoretical value $M_{\text{sat}-\text{theo}}^{\text{total}}=10.440{\mu }_{\text{B}}$ (Table 1).

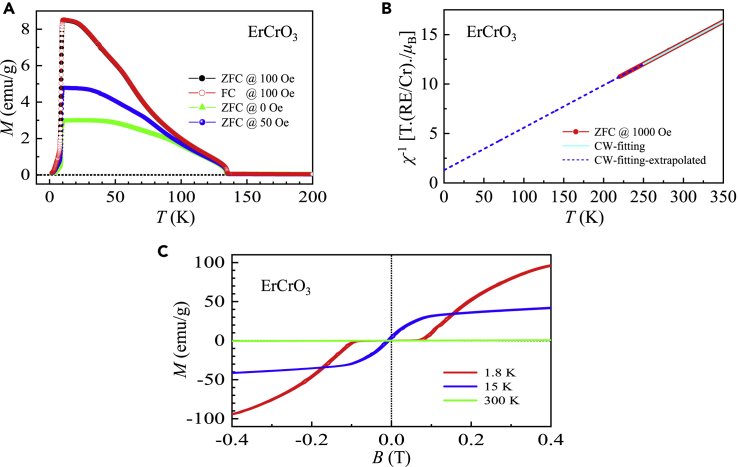
ErCrO₃

Below $T_{\text{N}}^{\text{Cr}}=135.4\left(1\right)\text{K}$ (Eibschütz et al., 1970), there was a small sharp enhancement in the magnetization within ∼ 0.72 K, which then increased smoothly until an onset of a sudden decrease at $T_{\text{SR}}^{\text{Cr}}\sim 9.7\text{K}$ (Figure 7A). The decrease in magnetization is attributed to the spin reorientation of Cr³⁺ ions from ${\Gamma }_4\left(G_x,A_y,F_z;F_z^R\right)$ to ${\Gamma }_1\left(A_x,G_y,C_z;C_z^R\right)$ or the ${\Gamma }_1\left(0\right)$ spin configuration (Su et al., 2010b, 2012). Below $T_{\text{N}}^{\text{Er}}\sim 8\text{K}$, the magnetization at 0, 50, and 100 Oe decreased linearly. No difference was found in the ZFC and FC magnetization at 100 Oe.

Figure 7.

Magnetic property of ErCrO₃

(A) Magnetization as a function of temperature from 1.8–200 K measured at 0, 50, and 100 Oe. We performed both zero-field and field-cooling measurements at 100 Oe.

(B) Zero-field cooling inverse magnetic susceptibility ${\chi }^{-1}$ (solid circles) at an applied magnetic field of 1000 Oe as a function of temperature in the range of 220–350 K. The solid lines represent the fits with a Curie-Weiss law from 250–350 K. The Curie-Weiss law fits were extrapolated to low temperatures shown as short-dashed lines.

(C) Magnetic hysteresis loops measured at low applied magnetic fields with selected temperatures.

The CW fitting resulted in an effective PM magnetic moment of 10.20 μ_B, in agreement with the theoretical value of 10.334 μ_B, and a CW temperature of $-$30.0(1) K (Figure 7B and Table 1).

No magnetic hysteresis loop appeared in the M-B measurements (Figure 7C). In contrast, clear hysteresis loops were observed previously for polycrystalline ErCrO₃ samples (Shi et al., 2018). For the magnetization curve at 1.8 K, a gate magnetic field of ∼ 650 Oe existed. When $0\le B\le B_{\text{gate}}=650\text{Oe}$, the magnetization increased linearly from 0 to ∼ 0.45 emu g^–1. Then, it quickly flattened when B ∼ 0.617 T and attained M_meas = 6.385(1) μ_B at 14 T (Figure S2E).

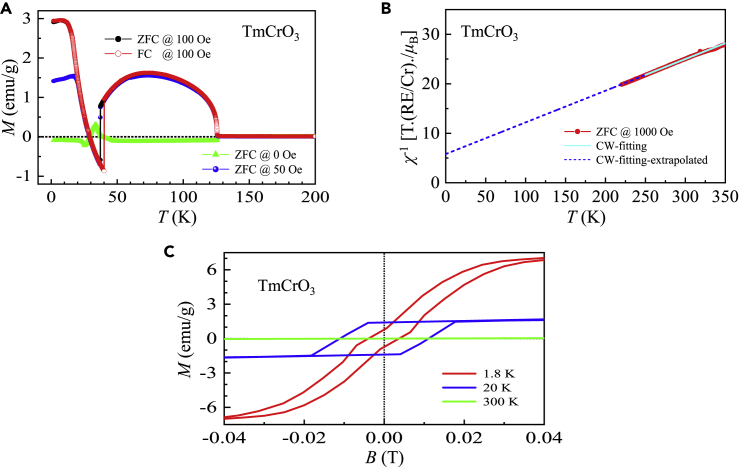
TmCrO₃

We determined that $T_{\text{N}}^{\text{Cr}}=125.9\left(1\right)\text{K}$ for the TmCrO₃ single crystal (Figure 8A), which is consistent with a previous study of polycrystalline TmCrO₃ (Wang et al., 2016a; Yoshii, 2012). Below $T_{\text{N}}^{\text{Cr}}$, the ZFC magnetization at 0 Oe was negative. The magnetization at 50 and 100 Oe was positive and increased sharply within ∼ 1 K. This is because Cr³⁺ spins order into a canted AFM state of the ${\Gamma }_2$ configuration $\left(F_x{C}_y{G}_z\right)$ (Tamaki et al., 1977; Yoshii, 2012). Upon further cooling, the magnetization increased smoothly until it reached a maximum at $T_{\max }^{\text{Cr}}\sim 74\text{K}$. After that, the magnetization reduced smoothly and attained negative values suddenly at T_SR ∼ 37.2 K (for ZFC at 50 and 100 Oe) and ∼ 40.1 K (for FC at 100 Oe), followed by a sharp increase with positive values appearing again at a compensation temperature T_comp ∼ 28.72 K. The sharp drop observed at ∼ 40.1 K could be ascribed to the spin reorientation of Cr³⁺ ions accompanied by a 90° rotation of the spins, that is, from one crystallographic axis to another, probably because of the competition between anisotropic exchanges and single-ion anisotropy (Li, 2016). This feature became smooth in the polycrystalline samples (Wang et al., 2016a; Yoshii, 2012). Our study revealed a reversal of the magnetization behavior. The ZFC and FC magnetization at 100 Oe nearly coincided with each other. This is different from the observations with polycrystalline TmCrO₃ (Yoshii, 2012). We observed a magnetic phase transition at $T_{\text{N}}^{\text{Tm}}\sim 19.6\text{K}$, which probably correlates with the AFM order of Tm³⁺ ions. This was not observed in polycrystalline TmCrO₃ samples (Wang et al., 2016a; Yoshii, 2012).

Figure 8.

Magnetic property of TmCrO₃

(A) Magnetization as a function of temperature from 1.8–200 K measured at 0, 50, and 100 Oe. We performed both zero-field and field-cooling measurements at 100 Oe.

(B) Zero-field cooling inverse magnetic susceptibility ${\chi }^{-1}$ (solid circles) at an applied magnetic field of 1000 Oe as a function of temperature in the range of 220–350 K. The solid lines represent the fits with a Curie-Weiss law from 250–350 K. The Curie-Weiss law fits were extrapolated to low temperatures shown as short-dashed lines.

(C) Magnetic hysteresis loops measured at low applied magnetic fields with selected temperatures.

We obtained μ_eff–meas = 8.35 μ_B, which is almost identical to the theoretical value ${\mu }_{\text{eff}-\text{theo}}^{\text{total}}=8.495{\mu }_{\text{B}}$, and ${\Theta }_{\text{CW}}=-90.6\left(4\right)\text{K}$ (Figure 8B and Table 1).

We observed different magnetic hysteresis loops (Figure 8C): (i) at 20 K, a parallelogram-shaped loop with M_r ∼ 1.4 emu g^–1 and B_c ∼ 111 Oe. (ii) At 1.8 K, a twisted loop with M_r ∼ 0.75 emu g^–1 and B_c ∼ 38.2 Oe. The magnetization reached M_meas = 2.868(1) μ_B at 14 T (Figure S2F and Table 1).

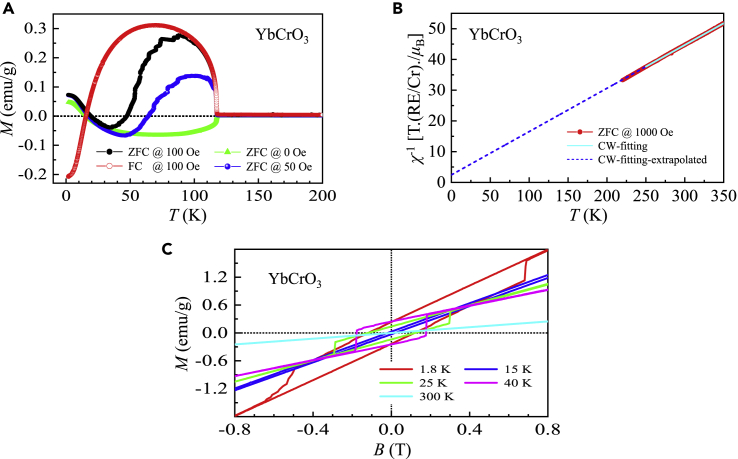
YbCrO₃

We determined that $T_{\text{N}}^{\text{Cr}}=117.9\left(1\right)\text{K}$ for the YbCrO₃ single crystal (Figure 9A), which is the lowest magnetic phase transition temperature of Cr³⁺ sublattices among all rare-earth orthochromates. Below $T_{\text{N}}^{\text{Cr}}$, the ZFC magnetization at 0 Oe reduced sharply to negative values, whereas the magnetization at 50 and 100 Oe increased sharply and attained the maximum values at $T_{\max }^{\text{Cr}}\sim 99.3\text{K}$ (for ZFC at 50 Oe), 86.3 K (for ZFC at 100 Oe), and 69.6 K (for FC at 100 Oe), followed by smooth decreases to negative values at compensation temperatures T_comp1 ∼ 63.7 K (for ZFC at 50 Oe), 47.5 K (for ZFC at 100 Oe), and 15.5 K (for FC at 100 Oe). The positive values of magnetization at 0, 50, and 100 (ZFC) Oe reappeared at T_comp2 ∼ 15.5 K (for ZFC at 0 Oe), 17.6 K (for ZFC at 50 Oe), and 19.5 K (for ZFC at 100 Oe), whereas the magnetization at FC 100 Oe still remained negative. Below $T_{\text{N}}^{\text{Yb}}\sim 7\text{K}$, all the ZFC magnetization curves flattened (Su et al., 2010a). Notably, a large difference exists between the curves of the ZFC and FC magnetizations at 100 Oe. The FC magnetization at 100 Oe resembles that observed in the polycrystalline samples (Wang et al., 2016b).

Figure 9.

Magnetic property of YbCrO₃

(A) Magnetization as a function of temperature from 1.8–200 K measured at 0, 50, and 100 Oe. We performed both zero-field and field-coolings measurements at 100 Oe.

(B) Zero-field cooling inverse magnetic susceptibility ${\chi }^{-1}$ (solid circles) at an applied magnetic field of 1000 Oe as a function of temperature in the range of 220–350 K. The solid lines represent the fits with a Curie-Weiss law from 250–350 K. The Curie-Weiss law fits were extrapolated to low temperatures shown as short-dashed lines.

(C) Magnetic hysteresis loops measured at low applied magnetic fields with selected temperatures.

The CW fitting resulted in μ_eff–meas = 5.63 μ_B, which was slightly lower than the theoretical value ${\mu }_{e\text{ff}-\text{theo}}^{\text{total}}=5.964{\mu }_{\text{B}}$, and ${\Theta }_{\text{CW}}=-17.4\left(4\right)\text{K}$ (Figure 9B and Table 1).

No magnetic hysteresis loop appeared in the ZFC M-B curves at 15 and 300 K, whereas we observed magnetic hysteresis loops with a similar shape at 1.8 K (M_r ∼ 0.24 emu g^–1; B_c ∼ 1200 Oe), 25 K (M_r ∼ 0.14 emu g^–1; B_c ∼ 1200 Oe), and 40 K (M_r ∼ 0.25 emu g^–1; B_c ∼ 1780 Oe) (Figure 9C). The measured magnetization M_meas = 0.883(1) μ_B at 1.8 K and 14 T, which is merely ∼ 17.7% of $M_{\text{sat}-\text{theo}}^{\text{total}}=5{\mu }_{\text{B}}$ (Figure S2G and Table 1).

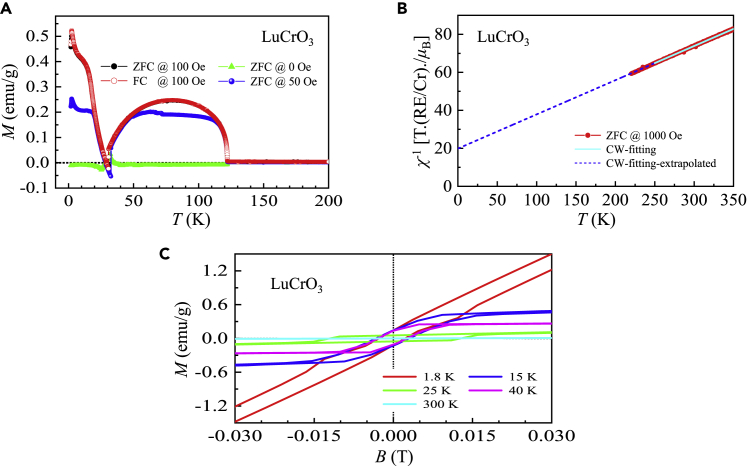
LuCrO₃

The LuCrO₃ single crystal exhibited magnetic behaviors similar to those observed in single-crystal TmCrO₃ (Figures 8A and 10A). We determined $T_{\text{N}}^{\text{Cr}}=122.3\left(1\right)\text{K}$, $T_{\max }^{\text{Cr}}\sim 79\text{K}$ (for ZFC and FC at 100 Oe), T_SR ∼ 33 K (for ZFC at 50 Oe) and 31 K (for ZFC and FC at 100 Oe), T_comp2 ∼ 28 K (for all data), and $T_{\text{N}}^{\text{Lu}}\sim 2.3\text{K}$ for the LuCrO₃ single crystal. No clear difference was observed in the ZFC and FC magnetization at 100 Oe. Our LuCrO₃ single crystal demonstrated magnetic behaviors different from those of previous polycrystalline samples (Durán et al., 2014).

Figure 10.

Magnetic property of LuCrO₃

(A) Magnetization as a function of temperature from 1.8–200 K measured at 0, 50, and 100 Oe. We performed both zero-field and field-cooling measurements at 100 Oe.

(B) Zero-field cooling inverse magnetic susceptibility ${\chi }^{-1}$ (solid circles) at an applied magnetic field of 1000 Oe as a function of temperature in the range of 220–350 K. The solid lines represent the fits with a Curie-Weiss law from 250–350 K. The Curie-Weiss law fits were extrapolated to low temperatures shown as short-dashed lines.

(C) Magnetic hysteresis loops measured at low applied magnetic fields with selected temperatures.

The CW fitting results in μ_eff–meas = 4.98 μ_B, which is ∼ 28.1% higher than the theoretical value ${\mu }_{\text{eff}-\text{theo}}^{\text{total}}=3.873{\mu }_{\text{B}}$, and ${\Theta }_{\text{CW}}=-110.4\left(2\right)\text{K}$ (Figure 10B and Table 1).

We observed magnetic hysteresis loops at: 1.8 K (M_r ∼ 0.13 emu g^–1; B_c ∼ 25 Oe), 15 K (M_r ∼ 0.14 emu g^–1; B_c ∼ 32 Oe), 25 K (M_r ∼ 0.054 emu g^–1; B_c ∼ 125 Oe), and 40 K (M_r ∼ 0.12 emu g^–1; B_c ∼ 28 Oe) (Figure 10C). The measured magnetization, M_meas 1.197(1) μ_B, at 1.8 K and 14 T is merely ∼ 39.9% of $M_{\text{sat}-\text{theo}}^{\text{total}}=3{\mu }_{\text{B}}$ (Figure S2H and Table 1).

We summarize the magnetic behaviors of single-crystal RECrO₃ compounds as follows: (i) TbCrO₃, DyCrO₃, and ErCrO₃ displayed similar temperature dependencies as did TmCrO₃ and LuCrO₃ single crystals. (ii) DyCrO₃ and ErCrO₃ did not exhibit negative magnetization, whereas the others did. (iii) Reversal magnetic behaviors (positive → negative → positive) occurred for TmCrO₃, YbCrO₃, and LuCrO₃ single crystals. (iv) We did not observe any indication of Eu³⁺ magnetic ordering, which may require lower temperatures. (v) Obvious magnetic hysteresis loops were observed for RECrO₃, except for ErCrO₃. (vi) The measured magnetization at 1.8 K and high magnetic fields plateaued for RECrO₃ (RE = Tb, Dy, Ho, Er, and Lu) single crystals. (vii) The measured effective PM moments of EuCrO₃ and LuCrO₃ were not consistent with the theoretical values. (viii) The applied magnetic field of 14 T was far less to saturate RECrO₃ at 1.8 K. (ix) Only HoCrO₃ demonstrated a positive CW temperature. Finally, we observed the complex and coupled magnetic phase transitions of RE³⁺ (except for Eu³⁺) and Cr³⁺ ions.

We also summarize the magnetic structures of RE³⁺ and Cr³⁺ ions in RECrO₃ (RE = Gd, Tb, Dy, Ho, Er, Tm, Yb, and Lu) compounds in the literature (Table 2). The magnetic SR transition of Cr³⁺ ions has been reported for GdCrO₃ (Cooke et al., 1974) and ErCrO₃ (Hornreich, 1978; Shamir et al., 1981) compounds. The detailed magnetic structures of Tm³⁺ and Yb³⁺ ions in TmCrO₃ (Shamir et al., 1981) and YbCrO₃ (Shamir et al., 1981) compounds remain controversial. A F_x magnetic component of Yb³⁺ ions had to be included for a satisfactory fit of the neutron powder diffraction data of YbCrO₃ in the temperature range of 1.5–120 K (Deepak et al., 2021). Unraveling the nature of the magnetic phase transitions necessitates neutron scattering studies on single-crystal samples with modern techniques (Li, 2008).

Table 2.

Summary of the previously reported magnetic structures of RE³⁺ and Cr³⁺ ions in RECrO₃ (RE = Gd, Tb, Dy, Ho, Er, Tm, Yb, and Lu) compounds

RECrO3	RE3+	Cr3+	SR	Cr3+
	$\left(T<T_{\text{N}}^{\text{RE}}\right)$	$\left(T<T_{\text{SR}}^{\text{Cr}}\right)$	(Cr3+)	$\left(T_{\text{SR}}^{\text{Cr}}<T<T_{\text{N}}^{\text{Cr}}\right)$
GdCrO3	FxCy	FxGz	√	GxFz
TbCrO3	FxCy	–	–	FxGz
DyCrO3	GxAy	–	–	FxGz
HoCrO3	−Fx−Cy	–	–	Gz
ErCrO3	−Cz	Gy	√	GxFz
TmCrO3	–	–	–	FxGz
YbCrO3	–	–	–	FxGz
LuCrO3	–	–	–	FxGz

The crystal structure is orthorhombic with the Pbnm space group (No. 62). Here $T_{\text{N}}^{\text{RE}}=\text{AFM}$ transition temperature of RE³⁺ ions; SR = spin reorientation; $T_{\text{SR}}^{\text{Cr}}=\text{SR}$ temperature of Cr³⁺ ions; $T_{\text{N}}^{\text{Cr}}=\text{AFM}$ transitions temperature of Cr³⁺ ions. The check mark (√) represents that there exists a magnetic SR phase transition. These were summarized from the following references: GdCrO₃ (Cooke et al., 1974), TbCrO₃ (Gordon et al., 1976), DyCrO₃ (Bertaut, 1963; Krynetskii and Matveev, 1997; Tamaki et al., 1975), HoCrO₃ (Shamir et al., 1981; Su et al., 2011), ErCrO₃ (Hornreich, 1978; Shamir et al., 1981), TmCrO₃ (Shamir et al., 1981), YbCrO₃ (Shamir et al., 1981), and LuCrO₃ (Shamir et al., 1981).

Discussion

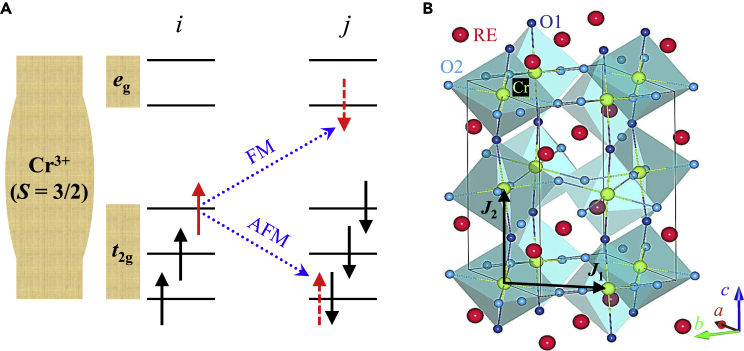
Superexchange interactions between the neighboring spins of transition metals can be realized through VCT via intermediate O^2– ions. During this process, the tilting of the oxygen octahedron corresponds to the change in the metal-oxygen-metal bond angles and may lead to t_2g and e_g orbital overlapping. This facilitates the hopping of $t_{2\text{g}\uparrow }$ electrons via the bridge of O^2– ions to occupy the empty e_g band and the interaction with filled $t_{2\text{g}\downarrow }$ electrons at the same site, that is, the intersite t-e orbital hybridization (Zhou et al., 2010; Zhou and Goodenough, 2008). In the framework of t-e hybridization, the superexchange parameter J consists of the following two parts (Zhou et al., 2010):

$$J=J^{\pi }-J_{\text{hb}}^{\sigma },$$ (Equation 2)

where $J^{\pi }$ denotes AFM coupling via the VCT of $t_{2\text{g}}^3-\text{O}-t_{2\text{g}}^3$, and $J_{\text{hb}}^{\sigma }$ represents FM coupling via the VCT of $t_{2\text{g}}^3-\text{O}-e_{\text{g}}^2$. Both processes are schematically depicted in Figure 11A for Cr³⁺ ions. For example, for a half-filled transition metal like ${\text{Fe}}^{3+}\left(t_{2\text{g}}^3{e}_{\text{g}}^2\right)$, the effect of t-e hybridization on superexchange interactions may not be evident because the electron hoppings of ${\text{Fe}}^{3+}\left(t_{2\text{g}\uparrow }^3\right)-{\text{O}}^{2-}{\text{Fe}}^{3+}\left(t_{2\text{g}\downarrow }^3\right)$ and ${\text{Fe}}^{3+}\left(t_{2\text{g}\uparrow }^3\right)-{\text{O}}^{2-}-{\text{Fe}}^{3+}\left(e_{\text{g}\downarrow }^2\right)$ themselves are AFM couplings already (Zhou et al., 2010; Zhou and Goodenough, 2008). In contrast, for less than half-filled 3d electrons like Cr³⁺ ions $\left(t_{2\text{g}}^3{e}_{\text{g}}^0\right)$ in RECrO₃ compounds, the t-e orbital hybridization favors the VCT of ${\text{Cr}}^{3+}\left(t_{2\text{g}\uparrow }^3\right)-{\text{O}}^{2-}-{\text{Cr}}^{3+}\left(e_{\text{g}}^0\right)$ (Qian et al., 2014; Siddique et al., 2021; Zhou et al., 2010). Electron hopping of $t_{2\text{g}}^3-\text{O}-e_{\text{g}}^0$ can increase the FM coupling component $J_{\text{hb}}^{\sigma }$. When RE³⁺ ions change from La to Lu in RECrO₃, the competition between the AFM $\left(J^{\pi }\right)$ and FM $\left(J_{\text{hb}}^{\sigma }\right)$ components would probably result in a variation in $T_{\text{N}}^{\text{Cr}}$.

Figure 11.

Process of virtual charge transfer and crystal structure

(A) Crystal field splitting of the 5-fold degenerate d orbitals of Cr³⁺ ions (3d³) in a cubic environment that splits the d-level into 2-fold degenerate e_g and 3-fold degenerate t_2g levels. The arrows represent the spins of chromium. We schematically show the virtual charge transfers, leading to FM and AFM states, respectively.

(B) Refined crystal structure of RECrO₃ in one unit cell (solid lines) with Pbnm space group (No. 62). The RE, Cr, O1, and O2 ions are labeled. J₁ and J₂ represent the NN spin-exchange parameters within the ab plane and along the c axis, respectively.

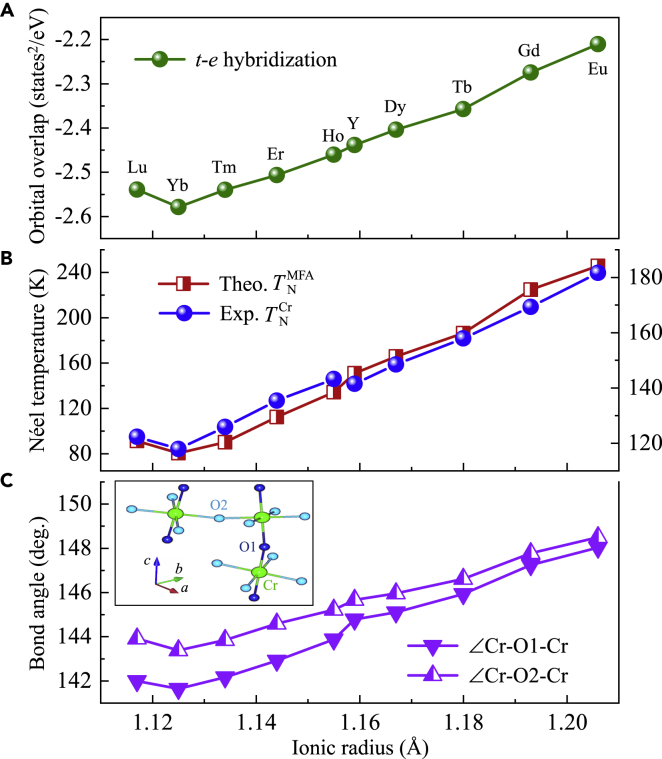
To quantitatively describe the Cr³⁺-O^2--Cr³⁺ superexchange interactions as well as the $t_{2\text{g}}-e_{\text{g}}$ (t-e) orbital overlapping degree as a function of the ionic radii of the RE³⁺ ions, we calculated the exchange parameters and electronic structures of RECrO₃ (RE = Y, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, and Lu) compounds. We mainly considered the NN exchange parameters of the Cr³⁺ sublattices within the crystallographic ab plane (J₁) and along the c axis (J₂) (Figure 11B). We extracted the values of J₁ and J₂ using the so-called energy mapping method with four types of magnetic structures (A-AFM, C-AFM, G-AFM, and FM) (Figure S3). We obtained the total energy of each magnetic structure using DFT calculations, projecting each collinear spin state onto the following spin Hamiltonian of a Heisenberg model

$$H=-\sum J_{ij}{S}_i\cdot S_j,$$ (Equation 3)

where J > 0 represents FM interactions, and J < 0 denotes AFM couplings. Using Equation (3), we can solve for J₁ and J₂ as (Bernal et al., 2021; Fujioka et al., 2008)

$$J_1=\left(E_G+E_C-E_A-E_F\right)/8S^2\text{,}\text{and}$$ (Equation 4)

$$J_2=\left(E_G-E_C+E_A-E_F\right)/4S^2\text{.}$$ (Equation 5)

Thus, we can calculate the Néel temperatures of the RECrO₃ compounds using the mean-field approximation (MFA) (Fujioka et al., 2008), that is,

$$T_{\text{N}}=\frac{2S\left(S+1\right)}{3k_B}\left(-4J_1-2J_2\right)\text{.}$$ (Equation 6)

To depict the hybridization degree, we calculated the overlap of $t_{2\text{g}\downarrow }$ and $e_{\text{g}\uparrow }$ (Table 3) using their DOS (Figure S4) product over the corresponding energy region.

$$I_{t_{2\text{g}\downarrow }-e_{\text{g}\uparrow }}={\int }_{E_{\text{F}}}^{E_{\text{c}}}{D}_{t_{2\text{g}\downarrow }}\left(E\right)D_{e_{\text{g}}\uparrow }\left(E\right)dE,$$ (Equation 7)

where $D_{t_{2\text{g}\downarrow }}\left(E\right)$ and $D_{e_{\text{g}\uparrow }}\left(E\right)$ are the DOSs for the $t_{2g\downarrow }$ and unoccupied $e_{\text{g}\uparrow }$ states of Cr³⁺ ions, respectively. E_F and E_c represent the Fermi level and cutoff energy of the $t_{2\text{g}\downarrow }-e_{\text{g}\uparrow }$ hybridization, respectively. With Equation (7), we could quantitatively describe the t-e hybridization in RECrO₃ orthochromates (Table 3).

Table 3.

Calculated nearest-neighbor (NN) exchange parameters J₁ and J₂, as well as the ratio J₂/J₁, Néel temperature $\left(T_{\text{N}}^{\text{MFA}}\right)$ based on the mean-field approximation, t-e orbital overlapping degree $\left(I_{t_{2\text{g}\downarrow }-e_{\text{g}\uparrow }}\right)$, and the ordered effective moment $\left(M_{{\text{Cr}}^{3+}}\right)$ of Cr³⁺ ions in RECrO₃ orthochromates

Parameter (unit)	J1 (meV)	J2 (meV)	J2/J1	$T_{\text{N}}^{\text{MFA}}$ (K)	$I_{t_{2\text{g}\downarrow }-e_{\text{g}\uparrow }}$ (states2/eV)	$M_{{\text{Cr}}^{3+}}$ (μB)
EuCrO3	−1.420	−1.390	0.98	245.7	−2.2104	2.933
GdCrO3	−1.330	−1.210	0.91	224.8	−2.2743	2.931
TbCrO3	−1.140	−0.940	0.82	186.5	−2.3571	2.929
DyCrO3	−1.050	−0.760	0.72	165.9	−2.4040	2.928
YCrO3	−0.990	−0.630	0.63	151.0	−2.4387	2.930
HoCrO3	−0.940	−0.430	0.46	134.3	−2.4602	2.928
ErCrO3	−0.850	−0.230	0.27	112.4	−2.5064	2.927
TmCrO3	−0.720	−0.120	0.17	90.2	−2.5396	2.926
YbCrO3	−0.690	−0.001	0.01	80.5	−2.5786	2.925
LuCrO3	−0.760	−0.046	0.06	91.3	−2.5394	2.925

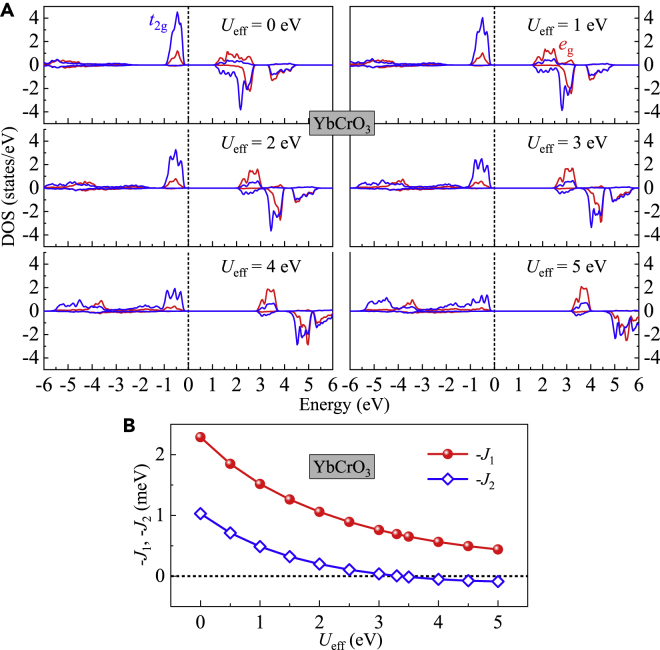
To illustrate the effect of on-site Coulomb interactions of Cr³⁺ ions on the superexchanges in rare-earth orthochromates, we chose YbCrO₃ as an example and carried out a calculation of U_eff scan from 0 to 5 eV as shown in Figure 12A, where we can see the U_eff-dependent evolution of t-e orbital hybridizations from the DOSs. Based on these calculations, the U_eff-dependent exchange parameters of J₁ and J₂ were extracted and shown in Figure 12B. The increase in on-site Coulomb interactions enhances both the crystalline-field splitting and the exchange splitting (with a relatively larger enhancement). The overall superexchange interactions could be expressed as (Zhou et al., 2010)

$$J=J_0[{\left(b^{\pi }\right)}^2-\eta {\left(b_{\text{hb}}^{\sigma }\right)}^2]\text{,}\text{and}$$ (Equation 8)

$$\eta \propto \frac{U+{\text{Δ}}_{\text{ex}}}{U+{\text{Δ}}_{\text{c}}}\text{,}$$ (Equation 9)

where U denotes the on-site Coulomb interactions, Δ_ex and Δ_c are the exchange splitting and the crystalline-field splitting, respectively (Zhou et al., 2010). In the RECrO₃ system, different RE³⁺ ions lead to different crystallographic structures of RECrO₃. The increase of U_eff favors the ferromagnetic component in the entire superexchange interactions, leading to a strong competition between ferromagnetic and antiferromagnetic components, and finally may result in $J_2>0$, that is, ferromagnetism would be generated along the crystallographic c axis.

Figure 12.

Calculated DOSs, J₁ and J₂ of YbCrO₃

(A) Calculated DOSs of t_2g and e_g orbitals (as marked) of Cr³⁺ ions in YbCrO₃ at U_eff = 0, 1, 2, 3, 4, and 5 eV. The positive and negative values represent high-spin and low-spin states, respectively. The vertical short-dotted lines at energy = 0 eV denote the Fermi level.

(B) Calculated exchange parameters J₁ (within the ab plane) and J₂ (along the c axis) as a function of U_eff for the YbCrO₃ compound. Related to Discussion.

Different U_eff-value settings have a relatively minor effect on the t-e hybridization; therefore, our calculations are based on the on-site Coulomb interactions between Cr³⁺ ions using Hubbard U_eff = 3.3 eV derived under the framework of a linear-response ansatz, which is in good agreement with the measured band gaps (Singh et al., 2018). Meanwhile, the electron dispersions are not largely influenced by fixing U_eff, which assures the calculation of reliable t-e orbital hybridizations of RECrO₃ orthochromates by considering only the influence of RE³⁺ ions.

Based on the foregoing discussion, we first optimized the structural parameters of RECrO₃ orthochromates (Tables S1 and S2) (Kumar et al., 2008). Our calculations also indicate that the G-type AFM is the most stable magnetic structure for all the RECrO₃ orthochromates (Figure S3 and Table S3). Subsequently, we extracted the optimized values of J₁, J₂, Néel temperature $\left(T_{\text{N}}^{\text{MFA}}\right)$, and the $t_{2\text{g}}-e_{\text{g}}$ orbital overlapping degree $\left(I_{t_{2\text{g}}-e_{\text{g}}}\right)$ (Table 3).

When RE³⁺ ions varies from Eu to Lu, the changes of the calculated $I_{t_{2\text{g}}-e_{\text{g}}}$ (Figure 13A), $T_{\text{N}}^{\text{MFA}}$ (Figure 13B), and ∠Cr-O1-Cr and ∠Cr-O2-Cr (Figure 13C) demonstrated a similar trend, indicating a strong correlation between them and a clear effect of the RE³⁺ radii (Winter, 2021) on the superexchange interactions. The calculated $T_{\text{N}}^{\text{MFA}}$ coincided with the experimental $T_{\text{N}}^{\text{Cr}}$ values (Table 1, Figure 13B). The average value $\left(⟨\angle \text{Cr}-\text{O}-\text{Cr}⟩\right)$ of the ∠Cr-O1(2)-Cr bond angles changed from 148.34° (EuCrO₃) to 142.81° (YbCrO₃) (Tables S1 and S2), leading to the t-e hybridization $\left(I_{t_{2\text{g}}-e_{\text{g}}}\right)$ changing from −2.2104 (EuCrO₃) to −2.5786 states²/eV (YbCrO₃) and the corresponding $T_{\text{N}}^{\text{MFA}}$ decreased from 245.7 (EuCrO₃) to 80.5 K (YbCrO₃) (Table 3). Therefore, the decrease in bond angles of ∠Cr-O1(2)-Cr facilitated t-e hybridization by enhancing the FM component $\left(J_{\text{hb}}^{\sigma }\right)$ within the entire superexchange interaction. Both our experimental and theoretical studies produced the minimum AFM transition temperature for YbCrO₃ in the system (Figure 13B), which is inconsistent with a previous study on polycrystal RECrO₃ samples, where the minimum T_N and $⟨\angle \text{Cr}-\text{O}-\text{Cr}⟩$, occurred to LuCrO₃ (Zhou and Goodenough, 2008).

Figure 13.

Coincidence between experimental and theoretical properties

(A) Calculated t-e orbital overlapping degree $\left(I_{t_{2\text{g}\downarrow }-e_{\text{g}\uparrow }}\right)$.

(B) Experimental $\left(T_{\text{N}}^{\text{Cr}}\right)$ (right) and calculated $\left(T_{\text{N}}^{\text{MFA}}\right)$ (left) AFM transition temperatures.

(C) Theoretically optimized values of ∠Cr-O1(O2)-Cr bond angles of RECrO₃ (RE = Eu, Gd, Tb, Dy, Y, Ho, Er, Tm, Yb, and Lu) compounds. Inset of (C) shows the geometry of bond angles. The horizontal axis represents ionic radii of RE³⁺ ions.

Our DFT calculations demonstrate that the magnetic anisotropy of Cr³⁺ sublattices can be tuned by RE³⁺ ions. The ratio of J₂/J₁ is a good parameter that inversely expresses anisotropy. It indeed reduces from J₂/J₁ ∼ 0.98 (EuCrO₃) to ∼0.01 (YbCrO₃) (Table 3) and strongly correlates with the values of the ∠Cr-O1(2)-Cr bond angles. The ∠Cr-O1-Cr angle was outside the ab plane, and its value was smaller than that of ∠Cr-O2-Cr within the ab plane (Inset, Figure 13C). Therefore, we infer that the VCT of $t_{2\text{g}\uparrow }^3-{\text{O}}^{2-}-t_{2\text{g}\downarrow }^3$ produces the major AFM spin interactions within the ab plane, whereas the VCT of $t_{2\text{g}\uparrow }^3-{\text{O}}^{2-}-e_{\text{g}}^0$ can generate strong FM couplings along the c axis. This is in good agreement with the previously proposed magnetic model (Van der Ziel and Van Uitert, 1969). The difference between the ∠Cr-O1(2)-Cr values increases when RE³⁺ varies from Eu to Lu, indicating that the competition between in-plane AFM interactions and out-of-plane FM couplings becomes increasingly strong with an enhancement of FM interactions. The largest difference between ∠Cr-O1-Cr and ∠Cr-O2-Cr occurred for YbCrO₃, leading to the smallest J₂/J₁ ratio (∼0.01), and thus the largest magnetic anisotropy.

The FM coupling $J_{\text{hb}}^{\sigma }$ directly acts on the overall Cr-O-Cr superexchange. This is induced by the $t_{2\text{g}}-t_{2\text{g}}$ orbital hybridization and could compete with AFM coupling, leading to an overall exchange $J=J^{\pi }-J_{\text{hb}}^{\sigma }$ (Zhou et al., 2010). The state of Cr³⁺, that is, the 3d³ configuration with half-filled $t_{2\text{g}}$ orbital and empty e_g orbital, makes it a special ion compared with other elements such as V, Fe, and Mn (Streltsov and Khomskii, 2008). By chemical engineering (Yaresko, 2008) or applying high pressure (Fita et al., 2021), one may strengthen $t_{2\text{g}}-t_{2\text{g}}$ hopping but simultaneously weaken $t_{2\text{g}}-t_{2\text{g}}$ hopping. Eventually, this could result in an overall FM component superexchange between neighboring Cr³⁺ cations. The weak ferromagnetism results from competition between the Heisenberg exchange and DM interactions in orthochromates. This is one case of an AFM structure with a small canting, leading to a noncollinear spin configuration and thus a net FM component. Unraveling the competing degree of different spin interactions necessitates inelastic neutron scattering studies on single-crystal orthochromates.

Conclusion

We have successfully grown a series of RECrO₃ (RE = Y, Eu–Lu) single crystals with a laser-diode FZ furnace. The grown crystals are centimeter (gram)-scale with a good quality. We performed magnetization measurements as functions of temperature and applied magnetic field, providing more reliable and intrinsic magnetic properties. We theoretically investigated the t-e hybridization by quantitatively calculating the t_2g and e_g orbital overlapping degree $\left(I_{t_{2\text{g}\downarrow }-e_{\text{g}\uparrow }}\right)$ based on DOS calculations. As RE³⁺ ions change from Eu to Lu, the calculated AFM transition temperatures demonstrate a similar trend with those determined experimentally. The changes in the ∠Cr-O1(2)-Cr bond angles strongly influence the weight factor of FM couplings within the entire superexchanges interactions by (dis)favoring the VCT of $t_{2\text{g}\uparrow }^3-{\text{O}}^{2-}-e_{\text{g}}^0$. This may be the origin of the weak ferromagnetism appearing within the main AFM matrix of RECrO₃. The difference between ∠Cr-O1(2)-Cr bond angles results in a magnetic anisotropy between within the ab plane and along the c axis. The change of t-e hybridization coincides well with that of ∠Cr-O1(2)-Cr and that of $T_{\text{N}}^{\text{MFA}}$. Our research sheds light on the origin of the intriguing magnetism in the RECrO₃ system.

Limitations of the study

The single crystal growth of orthochromates is extremely difficult. First, traditional FZ furnaces equipped with four IR-heating halogen lamps and four ellipsoidal mirrors (such as Model FZ-T-10000-H-VI-VPO-PC from Crystal Systems Inc.) cannot even access the melting temperature of orthochromates so that the seed and feed rods could not be melted, thus the crystal growth could not be performed. Second, the evaporation of Cr-based oxides is very heavy like a thick haze. Third, the process of crystal growth is time-consuming and labor-intensive, and one needs to optimize various growth parameters. Presently, we are unable to measure magnetic properties as a function of the crystallographic orientation because of technique difficulties, which is left for future work.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Yttrium(III) oxide	Alfa Aesar	CAS: 1314-36-9
Gadolinium(III) oxide	Alfa Aesar	CAS: 12064-62-9
Terbium(III, IV) oxide	Alfa Aesar	CAS: 12037-01-3
Dysprosium(III) oxide	Alfa Aesar	CAS: 1308-87-8
Holmium(III) oxide	Alfa Aesar	CAS: 12055-62-8
Erbium(III) oxide	Alfa Aesar	CAS: 12061-16-4
Thulium(III) oxide	Alfa Aesar	CAS: 12036-44-1
Ytterbium(III) oxide	Alfa Aesar	CAS: 1314-37-0
Lutetium(III) oxide	Alfa Aesar	CAS: 12032-20-1
Chromium(III) oxide	Alfa Aesar	CAS: 1308-38-9
Software and Algorithms
Origin2016	OriginLab Corporation	https://www.originlab.com/
OrientExpress	(Ouladdiaf et al., 2006)	https://neutronoptics.com/OrientExpress.html
VASP 5.4.4	(Kresse and Furthmüller, 1996a, 1996b)	https://www.vasp.at/

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Prof. Dr. Hai-Feng Li (haifengli@um.edu.mo).

Materials availability

This long-term project produced a series of RECrO₃ (RE = Y, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, and Lu) single crystals utilizing the innovative method described in the China Invention Patent (CN110904497B). We welcome potential collaborations.

Method details

Single crystal growth procedure and parameters

Using raw materials of Y₂O₃ (Alfa Aesar, 99.9%), Gd₂O₃ (Alfa Aesar, 99.9%), Tb₄O₇ (Alfa Aesar, 99.9%), Dy₂O₃ (Alfa Aesar, 99.9%), Ho₂O₃ (Alfa Aesar, 99.9%), Er₂O₃ (Alfa Aesar, 99.9%), Tm₂O₃ (Alfa Aesar, 99.9%), Yb₂O₃ (Alfa Aesar, 99.9%), Lu₂O₃ (Alfa Aesar, 99.9%), and Cr₂O₃ (Alfa Aesar, 99.6%), polycrystalline RECrO₃ samples were synthesized with solid-state reactions. We first obtained homogeneous polycrystalline powder with a single phase. After that, cylindrical feed rods with additional treatments (Li et al., 2021) were shaped by a hydrostatic pressure of ∼70 MPa (Wu et al., 2020; Zhu et al., 2020b). Then RECrO₃ single crystals were grown by a laser-diode floating-zone furnace (Model: LD-FZ-5-200W-VPO-PCUM). The floating-zone method assures no introduction of impurities (Li, 2008). The growth speed was fixed at 5–15 mm/h to attain a stable growth state. Due to the intense volatility of chromium oxides, we added extra 5–15% mole raw chromium oxide for the synthesis of polycrystalline samples and for the growth of single crystals.

Neutron Laue diffraction

To determine the quality of the grown single crystals, we performed a neutron Laue diffraction study on the diffractometer, OrientExpress, located at ILL, Grenoble, France. Simultaneously, we simulated the recorded neutron Laue patterns along the three crystallograhpic axes with the software of OrientExpress (Ouladdiaf et al., 2006) to confirm the quality of the grown crystals.

Magnetization measurements

Magnetization was measured using the option of a vibrating sample magnetometer of Quantum Design physical property measurement system. Small RECrO₃ single crystals (5–15 mg) were glued on a quartz sample holder with GE Varnish. The dc magnetization was measured at applied magnetic fields of 0, 50, and 100 Oe with zero-field cooling and field cooling modes in the temperature range of 1.8–400 K. The magnetic field dependent hysteresis loops were measured from −14 to 14 T at different temperatures within 1.8–300 K.

First-principles calculations

The first-principles calculations of RECrO₃ compounds were carried out within density functional theory. The exchange and correlation term in Kohn-Sham equation was treated with the Perdew-Burke-Ernzerhof (PBE) and (PBE + U) functionals (Perdew et al., 1996; Franchini et al., 2007a, 2007b; Shick et al., 1999) using the Vienna Ab-initio Simulation Package (Kresse and Furthmüller, 1996a, 1996b). The core electrons were frozen, and the projected-augmented-wave method was used (Kresse and Joubert, 1999). The Cr 3d4s, RE (RE = Eu–Lu) elements 5p5d6s, Y (4s4p5s4d), and O 2s2p electrons were treated as valence electrons. It is well known that the 4f orbitals are tightly localized in comparison to the d orbitals. In the present study, we aim mainly to unravel the effect of lattice variation on Cr³⁺-O²⁻-Cr³⁺ superexchange interactions, and the energy scale of RE³⁺-RE³⁺ exchange interactions is about two magnitudes smaller than that of Cr³⁺-Cr³⁺, hence the 4f electrons of lanthanide ions could be frozen reasonably. A Gaussian broadening of 0.05 eV was chosen. The set of plane-wave basis with an energy cutoff of 500 eV was used. Brillouin-zone integrations were performed with a Gamma-point-centered 7 × 7 × 5 Monkhorst-Pack k-point mesh (Monkhorst and Pack, 1976). The ionic relaxation was performed with a convergency criterion of 10⁻⁵ eV/primitive cell for each relaxation step and stopped moving when residual force <0.01 eV/Å. A convergency accuracy of 10⁻⁶ eV per conventional cell was chosen for subsequent static self-consistent calculations.

We first optimized the structures with collinear magnetic configurations of FM and A-type, C-type, and G-type AFM, to determine the magnetic ground state of each compound. Furthermore, to avoid an underestimation of the band gap, the Hubbard U value (U_eff = U − J) of each compound was calculated using the linear response ansatz (Dudarev et al., 1998; Cococcioni and de Gironcoli, 2005). With appropriate Hubbard U value, static electronic self-consistent calculations were performed using the (PBE + U) method to obtain the exact total energy of the four magnetic states. The exchange parameters, J_i, under classical Heisenberg model could be deduced with the energy mapping method, as does $T_{\text{N}}^{\text{Cr}}$ based on the mean-field approximation (MFA). Finally, the electronic structures of the RECrO₃ compounds were calculated with reading the charge density of ground state of the magnetic configuration.

Quantification and statistical analysis

Sensitivity analysis (one-at-a-time) was carried out to see the effects of parameters in the numerical model.

Published: April 15, 2022

Data and code availability

• •All data reported in this article will be shared by the lead contact upon request.
• •Code with instructions reported in this article will be shared by the lead contact upon request.
• •Any additional information required to reanalyse the data reported in this study is available from the lead contact upon request.