Fig. 1.

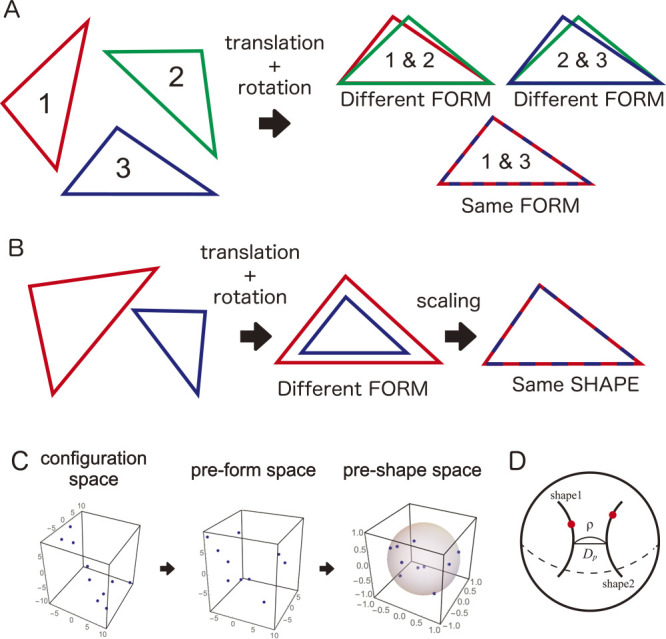
Shape as a geometric invariant. A. In geometric morphometrics, form is defined as a geometric invariant to translation and rotation. A pair of triangles 1–3 show the same form, but the pairs of 1–2 and 2–3 do not. B. The shape is defined as a geometric invariant to translation, rotation, and scaling. Two triangles cannot be matched with translation and rotation but can be matched with scaling included. C. Procrustes analysis is a process that extracts shape, i.e., removes positional, orientational, and size information. The landmark data, which are initially distributed in the configuration space, are constrained into subspaces via the Procrustes analysis. D. In the pre-shape space, the shape is represented as a trajectory of equivalence class against rotation. The differences between the trajectories are given by the great circular distance called the Procrustes distance. This figure was created based on Noshita (2021a) (Licensed under CC-BY 4.0).