Area under the curve may hide poor generalisation to external datasets

Area under the receiver operating characteristic curve (AUC) is a frequently used metric for measuring the performance of models trained using deep learning to predict whether a patient has a medical diagnosis or not. Of 12 published articles using deep learning to predict microsatellite instability (MSI) or DNA mismatch repair deficiency (dMMR) from scanned haematoxylin and eosin (H&E)-stained histopathology slides of colorectal cancer tissue,1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 only 1 (8%) study does not report the AUC⁷ and most studies also focus on the AUC in results and discussions. Other performance metrics are usually given less attention and too often not even reported. In particular, the conventional classification metrics sensitivity and specificity are reported in only 5 (42%) of the 12 studies.^4,5,8,9,12 This is unfortunate, as severe lack of generalisation could be completely hidden when only considering the AUC. In the extreme, a model always providing confident predictions of one specific class, for example, always predicting no MSI/dMMR with a high degree of confidence, could be associated with a perfect AUC of 1 despite being potentially harmful to patients if the model prediction is trusted and acted on in clinical practice.

Area under the curve

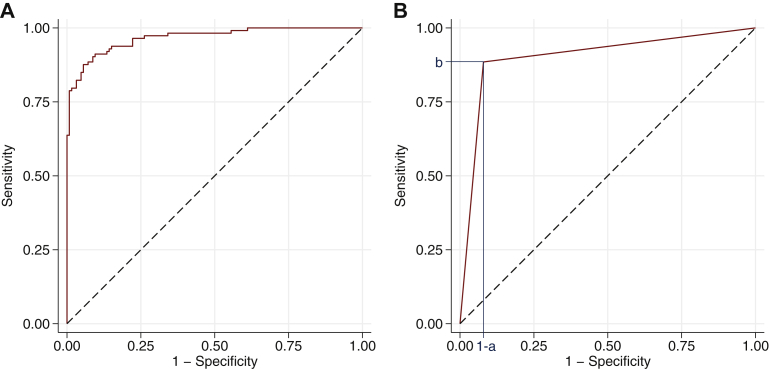
An AUC for a deep learning model predicting whether a patient has a medical diagnosis or not can be calculated on the basis of any given dataset. For each patient in the dataset, the model usually outputs a score intended to reflect the probability of the medical diagnosis. The AUC can then be calculated by gradually increasing a threshold from the minimum to the maximum score value, and for each threshold calculating the sensitivity and specificity obtained when classifying patients with a score above the threshold as positive and other patients as negative. The curve formed by drawing a straight line between all neighbouring pairs of sensitivity and 1-specificity is called the receiver operating characteristic (ROC) curve, and it is the area under this curve that is known as the AUC or AUROC. Figure 1A shows an example of an ROC curve.

Figure 1.

(A) An example of a receiver operating characteristic (ROC) curve. (B) An example of an ROC curve for a dichotomous marker with blue lines indicating its sensitivity b and its specificity a. This sum can be rewritten as AUC = [1–(1–a)]•b + (1–a)•b/2 + [1–(1–a)]•(1–b)/2 = a•b + (b–a•b)/2 + (a–a•b)/2 = (a + b)/2, which is the average of the marker’s sensitivity and specificity. The AUC of a dichotomous marker is the sum of the area of one rectangle and two triangles.

The AUC can be interpreted as the probability that a patient with the medical diagnosis has a higher model score than a patient without the medical diagnosis.¹³ This is easier to see from an alternative way of calculating the AUC, which is based on comparing each pair of patients where one patient has the medical diagnosis and the other patient does not have the medical diagnosis. The AUC is the proportion of such pairs where the model score is higher for the patient with the medical diagnosis. If the scores are equal, then that pair is considered half concordant, that is, contributing with a value of 0.5 instead of 0 or 1 for that particular pair. From this it is evident that a model outputting a range of unique scores, as deep learning models usually do, will have a higher AUC when using the scores directly than if first categorising them to be either predicted positive or predicted negative for the medical diagnosis, given that the order of the scores within the categories reflects the likelihood of the medical diagnosis at least slightly better than random guessing. The more conservative estimate, that is, the AUC of the model outputting either predicted positive or predicted negative, is simply the average of the sensitivity and specificity of that model (Figure 1B), which is a classification metric often referred to as balanced accuracy.

AUC in the presence of model bias

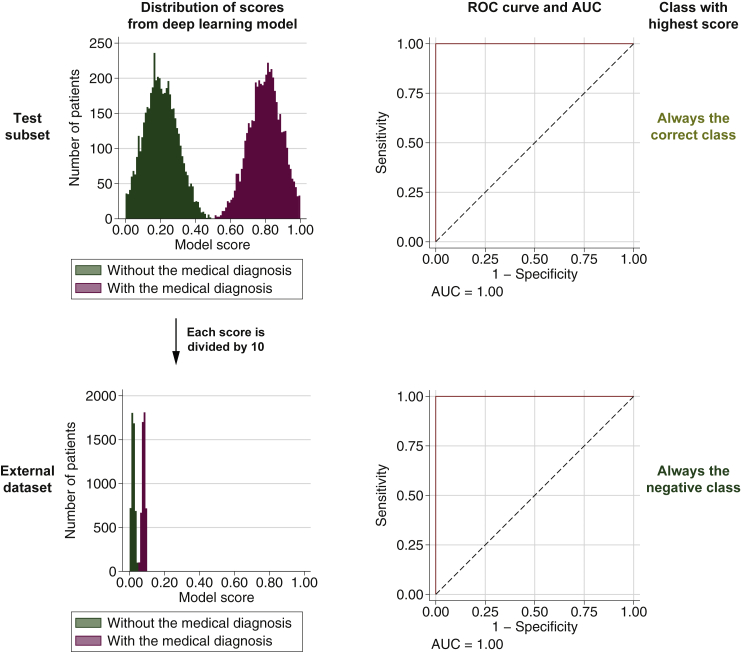
Assume there is a deep learning model predicting a medical diagnosis perfectly on a test subset of the dataset used to train the model. For the evaluation of an external dataset, assume that everything is identical as in the test subset except that all model scores are linearly scaled by dividing by 10. This implies that all scores will be ≤0.1 and the model would appear very confident that all patients are actual negatives, but this is false for the same number of patients as were actual positives in the test subset. Because the scores are just linearly scaled, the ranking of patients by the model score will in both the test subset and the external dataset correspond perfectly with whether the patient has the medical diagnosis or not, implying that the AUC will be 1 for both sets (see Figure 2 for an example). Thus the AUC is incapable of capturing the severe model bias, instead providing a performance measurement indicating perfect prediction also on the external dataset.

Figure 2.

Score distribution, receiver operating characteristic (ROC) curve with specification of the area under the curve (AUC), and classification for a model with a bias that causes a linear scaling of the model scores between a test subset and an external dataset. The two sets are identical except for this linear scaling.

In clinical practice, this model bias might result in patients being treated inappropriately. To understand why this can occur, imagine that the model is put into clinical usage in the setting represented by the external dataset. The model is applied as a part of the routine examination of individual patients, each time predicting that the patient does not have the medical diagnosis with a high degree of confidence. If the medical professionals would trust the model, which after all obtains a perfect AUC of 1 in precisely this clinical setting, it will result in patients with the medical diagnosis being treated as if they did not have the diagnosis, which could be potentially harmful. Because patients are considered only one or a few at a time, it might in practice take a long time for the medical professionals to realise that the model is actually always providing a score indicating very low probability of the medical diagnosis. Yet, if the very same patients were analysed retrospectively, the AUC would indicate that the model performs perfectly on those patients.

Real-world example where the AUC hides poor generalisation

Obviously, it would have been strange if all that separated the scores from a real model for a test subset and an external dataset would be a simple linear scaling. However, the fact that the AUC is not affected by a linear scaling of the scores, and more generally not affected by the application of any strictly increasing function, is a severe drawback of high practical relevance, in particular when evaluating the performance of deep learning models on external datasets. The reason is that deep learning models might be less resilient to inherent differences between datasets, caused by differences in, for example, patient demographics, sample preparation, or data acquisition. It is therefore important to use external datasets to check for model biases, and using only the AUC will hide one important type of bias that may occur.

In a recent study by Echle, Ghaffari Laleh, and colleagues,¹² deep learning models were trained to predict MSI/dMMR from scanned H&E-stained slides and evaluated on nine datasets consisting of 8343 patients in total. The highest AUC of 0.96 (95% confidence interval 0.94-0.98) was observed for the resection dataset from the Yorkshire Cancer Research Bowel Cancer Improvement Programme (YCR-BCIP), which consisted of 805 patients. The authors should be commended for extending their evaluations to include other performance metrics, in particular the sensitivity and specificity of models predicting either positive or negative for MSI/dMMR using thresholds found irrespective of the external dataset. When using either of the thresholds found suitable for most datasets, which were a fixed threshold at 0.25 and a threshold learned from the development dataset (this threshold was 0.289 when the YCR-BCIP dataset was the external dataset), the sensitivity was 99% but the specificity was only 8% and 15%, respectively. Because the authors also provided plots of the score distribution for each dataset, it is possible to see that the poor specificity is a consequence of generally higher model scores for the YCR-BCIP dataset than for other datasets. Thus there appears to be a severe model bias that limits the generalisation to the clinical setting represented by the YCR-BCIP dataset.

Not just the AUC can hide poor generalisation

While the popularity of the AUC makes its severe drawback for evaluations of external datasets a particular concern, there are also other common approaches to performance evaluation that suffer from the same drawback. One example is Harrell’s concordance index (c-index), which can be seen as a generalisation of the AUC to time to event data.¹⁴ Like the AUC, the c-index can be calculated using only the ranking of patients by their model scores, not the actual score values. In general, any metric that only uses the ranking will be invariant to any strictly increasing transformation of the model scores and thus not be able to capture model biases that affect only the absolute score values and not their relative ordering. A possible solution to this is to first categorise the scores using some predefined thresholds or rule, for example, select the class with highest score. Because transformations that only affect the absolute score values will still affect the classifications of the patients and that would also influence the ranking of patients by their classifications, in particular in terms of which patients have the same rank, the AUC and c-index should be lower on datasets where a model bias has resulted in such transformations of the scores. An alternative would be to use performance metrics that are calculated using classifications (e.g. sensitivity, specificity, and balanced accuracy).

If applying classifications to measure the performance, it is important that the external dataset does not affect the thresholds or rule used for categorisation. This will make it possible to classify individual patients without first adapting the categorisation to the external dataset. If this is not enforced, then the performance measured using classifications can also hide model biases that affect the absolute scores values and not the ranking of patients by the scores. For instance, assume that a threshold for dichotomisation is found as the score value at which 95% sensitivity is obtained for the external dataset. This threshold is then applied to measure the specificity on the same external dataset. For the artificial example described earlier, the adaption of the threshold to the external dataset will result in an identical specificity on the test subset and the external dataset, thus not revealing the severe model bias that cause the model scores to be very different in the two sets. The study by Echle, Ghaffari Laleh, and colleagues¹² includes a real-world example of the same issue. The specificity at 95% sensitivity was 89% for the YCR-BCIP dataset, larger than for any of the eight other external datasets, and in sharp contrast to the specificity of 8% for the fixed threshold of 0.25 and the specificity of 15% for the threshold learned from the development dataset.

It might be argued that a model with such biases is applicable in clinical practice as long as an appropriate threshold is identified individually for each clinical setting. Besides severely hampering clinical implementation, the use of individual thresholds does not remove the model bias in itself. As the precise reasons and manifestations of this model bias are unlikely to be fully understood, it will be difficult to know when the model predictions can be trusted and when a recalibration of the threshold is necessary because of changes occurring over time. Therefore a better alternative is to develop models without such biases and use thresholds or rules for categorisation that are not affected by external datasets. Invariances to inherent differences between datasets and clinical settings might be possible to obtain by controlling the capacity of the deep neural network and facilitating learning, but more direct approaches to encourage such invariances include data normalisation and data augmentation. Echle, Ghaffari Laleh, and colleagues¹² did apply data normalisation, but no data augmentation was used. A previous study by Tellez and colleagues¹⁵ suggests that colour data augmentation is essential to obtain deep learning models with good generalisation to external datasets when analysing scanned H&E-stained slides. They observed best performance when only using a particular data augmentation approach and good performances with various combinations of data normalisation and data augmentation approaches, but poor performance when using data normalisation and no colour data augmentation.

Outlook

Moving away from the extensive focus on the AUC of the model scores will increase the knowledge gained from deep learning studies evaluating external datasets by making it possible to identify which models suffer from an important type of bias, provided that the models are instead evaluated using thresholds or rules for categorisation of the model scores that are not adapted to the external datasets. This will facilitate more realistic performance measurements of deep learning models, in particular when combined with a decision on the primary analysis prior to evaluation of the external dataset, as this will avoid the multiple comparisons problem.¹⁶ In turn, the more truthful performance estimates will better guide the development of deep learning models capable of generalising well to the routine clinical practice despite differences in, for example, patient demographics, sample preparation, or data acquisition.

As for prediction of MSI/dMMR from scanned H&E-stained slides, it appears necessary to develop more robust models with high classification performance before considering clinical implementation. If the studies by Yamashita and colleagues⁸ and Echle, Ghaffari Laleh, and colleagues¹² represent the beginning of an increasing focus on more realistic performance estimations in this prediction task, then it appears likely that model biases will be rectified and that models applicable for clinical implementation will soon emerge.