SUMMARY
In high-throughput functional genomic screens, each gene product is commonly assumed to exhibit a singular biological function within a defined protein complex or pathway. In practice, a single gene perturbation may induce multiple cascading functional outcomes, a genetic principle known as pleiotropy. Here, we model pleiotropy in fitness screen collections by representing each gene perturbation as the sum of multiple perturbations of biological functions, each harboring independent fitness effects inferred empirically from the data. Our approach (Webster) recovered pleiotropic functions for DNA damage proteins from genotoxic fitness screens, untangled distinct signaling pathways upstream of shared effector proteins from cancer cell fitness screens, and predicted the stoichiometry of an unknown protein complex subunit from fitness data alone. Modeling compound sensitivity profiles in terms of genetic functions recovered compound mechanisms of action. Our approach establishes a sparse approximation mechanism for unraveling complex genetic architectures underlying high-dimensional gene perturbation readouts.
In brief
Pan et al. infer gene multifunctionality from high-dimensional gene perturbation data by applying sparse representation learning to large CRISPR-Cas9 fitness screens.
Graphical Abstract
INTRODUCTION
Genome-scale genomic and proteomic profiling has dramatically increased the scale of biological data acquisition. These technological advances have created a concomitant need for robust pattern recognition approaches that distill biological insights from the information and structure of large datasets. In particular, CRISPR-Cas9 technology has made gene perturbation a routine practice, and genome-scale screens can be readily performed across diverse cell contexts to measure physiological outcomes such as cell fitness. After collecting such datasets, a key challenge is to infer the genetic architecture underlying the observed fitness effects, such that individual genes become mapped to putative biological functions essential in specific cell contexts for cell fitness.
A foundational aspect of genetic architecture is pleiotropy, which states that gene products can participate in multiple independent biological functions. Pleiotropy helps explain how biological complexity arises from a finite collection of genetic elements (Wagner and Zhang, 2011). Pleiotropy has been observed across model organisms and at many scales of biological organization (Kinsler et al., 2020; Tyler et al., 2016; Wang et al., 2010), including in genetic variants that cause multiple human diseases (Gratten and Visscher, 2016; Solovieff et al., 2013; Watanabe et al., 2019).
Although pleiotropy is pervasive, our ability to account for pleiotropy within collections of cell fitness screens is limited. Because each gene perturbation is measured across many cell contexts with varied rate-limiting functional requirements (Henkel et al., 2019), to capture pleiotropy, one must first describe a set of biological functions that vary independently across cell contexts and then define a one-to-many mapping of genes to these functions. Both of these steps are challenging to perform in high-dimensional data, and the lack of a unified conceptual framework results in different calculations of pleiotropy that cannot be directly compared (Costanzo et al., 2016; Dudley et al., 2005; Koch et al., 2017). More commonly, analyses side-step pleiotropy by assuming a one-to-one mapping of genes to functions via gene clustering. A principled account of pleiotropy could reveal the cascading effects of gene perturbation through distinct aspects of cell fitness, thereby charting the flow of biological information between cellular functions that is currently absent from most functional genomics analyses (Fraser and Marcotte, 2004).
Here, we propose a framework that exploits pleiotropy to structure latent representations of biological function learned from fitness data. Our approach (Webster) takes a large gene perturbation matrix as input and infers a set of biological functions, which we refer to as a dictionary, such that each gene perturbation can be approximated as a combination of a small number of these dictionary elements. Regularizing the dictionary using the gene co-fitness graph results in individual dictionary elements mapping to interpretable biological modules. By applying Webster to CRISPR-Cas9 fitness screen collections performed in human cells under a variety of conditions, we explored the layers of functional impact resulting from single gene perturbation; jointly embedded gene and functional dependencies to chart fitness landscapes; prioritized genes and contexts for exploration of a learned function; and projected new perturbations into the learned reference space.
RESULTS
Theoretical overview of learning gene function representations with Webster
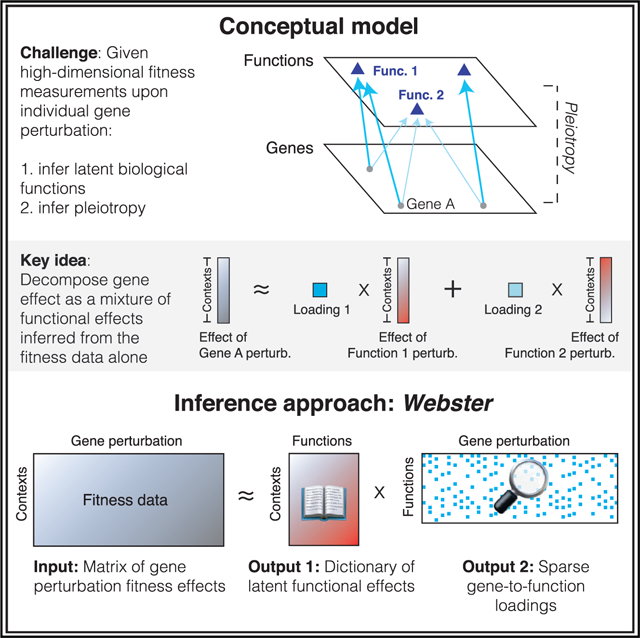
We define a biological function as a molecular process arising from interacting gene products (Keeling et al., 2019). We assume that physiological properties of a cell, such as its fitness, are controlled by a core set of functions, and that these functions can be distinguished by their independently varying activity levels across diverse cell contexts. Gene perturbations induce changes in one or more of these functions, thereby altering cell fitness.
Given a set of gene perturbation measurements, we wish to infer a dictionary of latent variable elements, such that the effects of each gene perturbation can be approximated as a mixture of dictionary elements. Furthermore, dictionary elements should correspond to interpretable biological functions learned empirically from the data with no outside knowledge. To perform this inference, we employed dictionary learning via Webster (Figure 1). Webster receives as input an n × m matrix of fitness effects, where n is the number of cell contexts, and m is the number of genes. Each fitness effect captures the change in cell number upon gene perturbation.
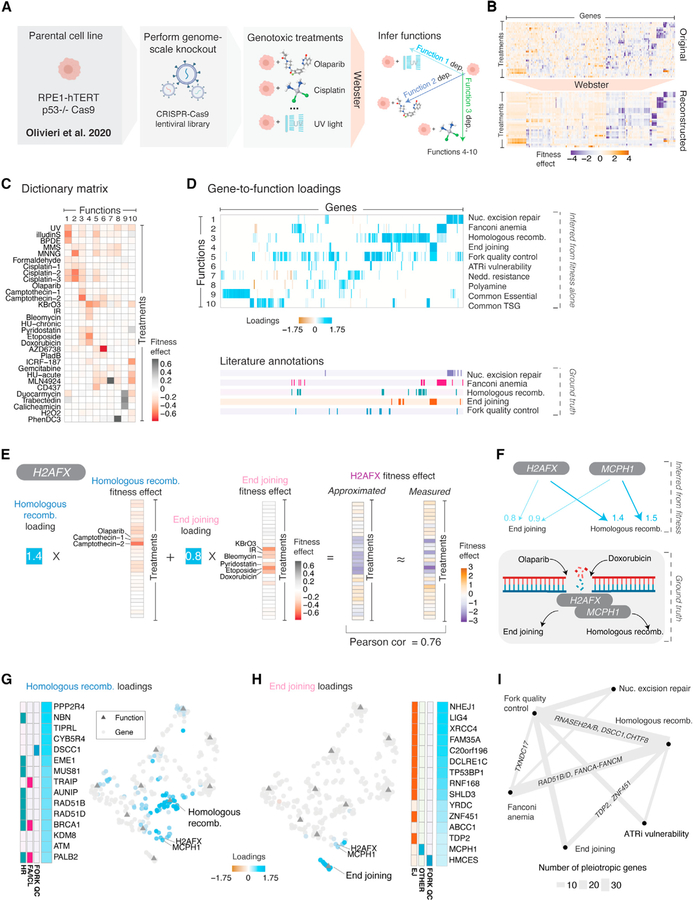
Figure 1. Pleiotropy underlying the fitness effects of gene perturbation can be approximated using dictionary learning.
(A) Fitness screen collections measure changes in cell growth rate following gene perturbation across diverse cell contexts. Webster applies graph-regularized dictionary learning to these data to discover latent variables corresponding to biological functions. Webster returns (1) a dictionary matrix containing the fitness effect of perturbing each inferred biological function and (2) sparse gene-to-function loadings. Using this information, each measured gene effect can be approximated as a sparse linear combination of these latent functional effects, scaled by the appropriate loadings. Given the number of latent functions (k) and a sparsity parameter (t), Webster minimizes the total approximation error while preserving the local structure of genes and cell contexts in its reduced-dimensional representations (see also Figure S1A).
(B) A generative example. Fitness effects corresponding to two distinct biological functions are generated over 25 cell contexts, shown in a heatmap, with a negative score indicating a slowed growth rate.
(C) Top: diagram of gene-to-function relationships. Gene C influences both functions, representing pleiotropy. Bottom: A gene’s contribution to each function is captured in a loading score, shown in a heatmap.
(D) To simulate the fitness effect of knocking out each gene, we scaled the appropriate functional effects with the loading scores defined in C, adding random noise to represent measurement error.
(E) This results in a synthetic screening dataset of 100 gene perturbations across 25 cell contexts, with the original biological functions implicit in the structure of the data. This matrix is the sole input to Webster.
(F) From this dataset, Webster was parameterized to infer two functional effects and model each gene effect as a mixture of both functional effects. Webster recovered a dictionary matrix that matched the ground truth defined in (B), and a gene-to-function loadings matrix that matched the ground truth defined in (C).
(G) Webster reconstructed each noisy gene effect measurement as a sparse linear combination of learned functional effects, thereby accommodating pleiotropy. For example, Webster accurately modeled knockout of Gene C as a near-equal mixture of knocking out Function 1 and Function 2 while isolating measurement noise in the model residuals.
Webster models the fitness effect matrix in terms of k latent biological functions learned from the data, with k < m and n. The output of Webster is two low-rank matrices: (1) an n × k dictionary matrix capturing the fitness effect of losing one of k inferred functions across n cell contexts and (2) a k × m loadings matrix encoding the sparse approximation of each of m gene effects in terms of t dictionary elements, with t ≪ k. This “sparse dictionary learning” approach (Rubinstein et al., 2010) has connections to sparse matrix factorization and dimensionality reduction (Cleary et al., 2017; Kim and Park, 2007; Stein-O’Brien et al., 2018).
In practice, Webster encompasses three steps: (1) preprocessing raw fitness data, (2) dictionary initialization with k-medoids, and (3) graph-regularized dictionary learning. Preprocessing removes low-variance gene effects and corrects batch effects between cell contexts prior to dictionary learning. Then, k-medoids defines an initial k × n dictionary that clusters the data. From this starting point, dictionary learning is performed using an objective function balancing (1) approximation error, (2) smoothness over a nearest-neighbor graph of genes, and (3) smoothness over a nearest-neighbor graph of cell contexts. This is performed via dual-graph-regularized k-SVD (Yankelevsky and Elad, 2016, 2020), which optimizes k overlapping subspaces of genes and takes the first eigenvector of the subspace as its representative dictionary element. Each gene effect is then linearly approximated using t dictionary elements via orthogonal matching pursuit (Pati et al., 1993), thereby capturing statistically independent components of variance. Further details are captured in STAR Methods under “Method details.”
A generative model of fitness data
As a primer, we established a simple generative model for fitness data and illustrate the use of Webster on generated data. We suppose two independent biological functions with measurable fitness effects upon loss across cell contexts (Figure 1B). We also suppose two classes of genes regulating either Function 1 or 2 and a third class of pleiotropic genes that weakly regulate both functions. We represented these gene-to-function relationships with loadings, which are high for genes that strongly activate a function or zero when the gene is unrelated (Figure 1C). To synthesize fitness effects of individual gene perturbation, we scaled the fitness effect of each function by the respective loading of that gene and added measurement noise (Figure 1D).
The resulting synthetic fitness data consisted of noisy gene perturbation effects across cell contexts, with fitness effects of both functions now latent in the structure of the data (Figure 1E). Using this data as the sole input, we parameterized Webster to infer two dictionary elements and approximate each gene perturbation as a mixture of both elements. The dictionary elements properly recovered the fitness effects of both functions across cell contexts. Furthermore, each gene effect was properly loaded onto the correct dictionary element (Figure 1F). In particular, pleiotropic genes were successfully decomposed as equal mixtures of both dictionary elements (Figure 1G). In comparison, clustering genes into functional groups failed to capture these pleiotropic relationships (Figure S1B), while standard latent variable models failed to resolve interpretable components (Figure S1C).
Learning representations of DNA damage functions from genotoxic fitness screens
Next, we applied Webster to published CRISPR-Cas9 fitness screens in a human cell line exposed to a diverse set of genotoxic stressors (Figure 2A) (Olivieri et al., 2020). Preprocessing the 31 genome-scale screens yielded 304 high-variance fitness genes (Figure S2A). After a hyperparameter sweep (Figure S2B), Webster successfully reconstructed the original gene perturbation data using an inferred dictionary composed of 10 elements, using two dictionary elements to represent each gene perturbation (Figure 2B; Table S1).
Figure 2. Pleiotropy underlies the DNA damage response to genotoxins in a human cell line.
(A) The immortalized human cell line RPE1-hTERT harboring a genome-scale CRISPR-Cas9 knockout library was subjected to 31 genotoxic stressors at a sublethal dose, resulting in a genotoxic fitness screen collection (Olivieri et al., 2020). From this data matrix, Webster was parameterized to infer 10 biological functions and approximate each gene effect as a sparse mixture of two functional effects.
(B) Top: the original fitness data, preprocessed to a set of 304 high-variance fitness gene effects from 31 treatment conditions, shown as a hierarchically clustered heatmap. Bottom: Webster’s approximation of the data, with each gene effect approximated as a sparse mixture of two inferred functions. The order of genes and treatments is preserved between panels.
(C) The dictionary matrix. Each column of the dictionary captures the inferred fitness effect of depleting an biological function learned from the data.
(D) The loadings matrix. Top: Sparse gene-to-function loadings for the 304 fitness genes. Each gene (column) has two nonzero loadings, encoding the model’s sparse representation of its gene effect. Bottom: Literature curated gene annotations, defined by Olivieri et al. (2020). Gene order is preserved between panels. TSG, tumor suppressor gene.
(E) Gene effect decomposition. Webster decomposes H2AFX knockout as a mixture of two functional effects related to DNA double-stranded breaks. The first function, homologous recombination, has a fitness effect induced by olaparib and camptothecin, etc. The second, end joining, has a fitness effect induced by doxorubicin and etoposide, etc. Webster faithfully modeled the H2AFX gene effect as the sum of these two functional effects, scaled by their respective loadings (Pearson = 0.76).
(F) Top: relationships learned from fitness data for H2AFX and MCPH1, an obligate H2AFX interactor. Each arrow corresponds to an inferred gene-to-function loading. Bottom: Illustration of H2AFX/MCPH1’s shared roles as DNA double-stranded break sensors upstream of homologous recombination and end joining.
(G) Additional gene loadings. Left: The top 15 genes ranked by their loadings on homologous recombination alongside literature annotations, as previously described in D. Right: Joint UMAP embedding of gene and functional effects, with genes colored by loading scores. Gene effect data from Olivieri et al. (2020). Functional effects inferred with Webster (this study) (see also Figure S2D).
(H) Same as (G), but for end joining gene loadings. In the UMAP, H2AFX and MCPH1 are embedded between homologous recombination and end joining. Gene effect data from Olivieri et al. (2020). Functional effects inferred with Webster (this study).
(I) A network of DNA damage functions, with the number of pleiotropic genes connecting functions represented by line thickness.
We matched each dictionary element to a biological function by annotating its most sensitive genotoxic stressors and its top-loaded genes, using literature resources that were hidden during model training. For example, DNA adducts are harmful to cell growth unless excised by nucleotide excision repair (NER). Using only numerical fitness data as input, Webster’s first dictionary element captured the negative fitness effects of DNA adduct-inducing agents (UV light, illudin S, and BPDE) (Figure 2C). The top four genes loaded on this dictionary element were classical NER pathway members (ERCC8, GTF2H5, UVSSA, and ERCC5), and the fifth (STK19) was a recently discovered pathway member (Boeing et al., 2016; Olivieri et al., 2020). Indeed, the strength of a gene’s loading on this element was a sensitive and specific predictor of NER pathway membership (Figure S2C, AUROC = 0.9). In the absence of prior knowledge, Webster inferred the existence of NER by discovering a fitness effect specific to DNA adduct-inducing agents, storing that effect as an element in the dictionary, and using it to model gene effects of NER pathway members.
We identified other dictionary elements that captured the effects of biological pathways, such as the sensitivity of cells to DNA-alkylating agents upon loss of Fanconi anemia/interstrand crosslink repair; topoisomerase I poisons upon loss of homologous recombination; topoisomerase II poisons upon loss of end joining; and polymerase alpha inhibitors upon loss of fork quality control (Figure 2C). Classical pathway members were specifically loaded onto the appropriate dictionary elements (Figure 2D). In contrast, commonly used latent variable models failed to separate these independent pathways into individual components (Figure S2C).
Webster’s dictionary also captured the effects of specific stressors that defined unique fitness outcomes in the data (Figure 2C). One dictionary element captured ATRi resistance, and top-loaded genes on this element overlapped with hits from previous ATRi resistance screens (Hustedt et al., 2019). Another element captured neddylation resistance, whose top-loaded gene (BEND3) was recently verified in an orthogonal study (Barghout et al., 2021). The top-loaded gene upon the PhenDC3 sensitivity element was SLC18B1, reflecting control of polyamine production by metastable RNA G-quadruplexes (Lightfoot et al., 2018). Finally, two dictionary elements captured the high intrinsic fitness effect of essential genes (Hart et al., 2015) and proliferation suppressor genes (Colic et al., 2019), which are technical factors commonly identified in screens of this design. From the fitness data alone, Webster learned a set of maximally informative dictionary elements capturing the functional effects of losing biological pathways that respond genotoxic stress.
Pleiotropy underlies the DNA damage response
We next examined how learned mixtures of functional effects approximated pleiotropic gene effects. The H2AFX histone protein is phosphorylated in response to DNA double-stranded breaks. Webster approximated the effect of perturbing H2AFX as a mixture of two functional effects scaled by their loadings (Pearson correlation [cor] = 0.76, Figure 2E):
Each loading quantifies the influence a gene exerts on a biological function and is expressed in units of standard deviation (SD) in the original fitness data. As such, homologous recombination contributes 1.4 SD to the H2AFX gene effect, and end joining contributes 0.8 SD. Because each gene is reconstructed from normalized, orthogonal dictionary elements, loadings are proportionally representative; that is, two-third of the H2AFX fitness effect is explained by its influence on homologous recombination and one-third by its influence on end joining.
MCPH1 is an obligate H2AFX interactor at double-stranded break sites. Webster approximated the effect of depleting MCPH1 using identical functional effects and similar loadings (Figure 2F). Homologous recombination and end joining both repair double-stranded breaks but are preferentially activated under different conditions (Figures 2E and 2F). By constraining Webster to approximate a large number of gene perturbations with a small number of dictionary elements, it parsimoniously modeled perturbations of double-stranded break sensors as mixtures of the underlying double-stranded break repair pathways.
To globally visualize these relationships, we used Uniform Manifold Approximation and Projection (UMAP) to plot genes and functions according to the similarity in fitness effects across cell contexts (Table S2). In general, genes are co-segregated by function on the map (Figures 2G and 2H), with pleiotropic genes such as H2AFX and MCPH1 occupying regions between functions. As another example, RAD51B was approximated as
in the original data and embedded between both functions by UMAP, reflecting its role as a homologous recombination gene and risk allele for Fanconi anemia (Ameziane et al., 2015) (Figure S2D).
The pleiotropy of human DNA damage genes mirrors observations in Drosophila, in which “even the best understood DNA repair pathways have unforeseen levels of complexities” (Sekelsky et al., 1998). We account for this complexity by modeling gene effects as combinations of functional fitness effects, thereby charting the flow of information between pathways activated by distinct genotoxic stressors (Figure 2I). Because our model is linear, these archetypes form the basis for an interpretable latent space of DNA damage functions, in which linear algebra operations reflect the underlying structure of pleiotropic gene relationships. For instance, H2AFX − End Joining + Fanconi Anemia ≈ RAD51B in our model (Pearson cor = 0.69, Figure S2E). This is analogous to linear semantics underlying word embeddings in which king − man + woman ≈ queen (Mikolov et al., 2013).
Learning representations of biological functions from cancer cell line fitness screens
Next, we scaled Webster to a ~20 times larger dataset of 675 cancer cell line fitness screens, the Cancer Dependency Map (Meyers et al., 2017) (Figure 3A). We preprocessed the data to include 2,921 gene effects exhibiting high variance across cell lines. After a hyperparameter sweep (Figures S3A and S3B), we recovered 220 dictionary elements and approximated each gene effect using up to four dictionary elements (Figure 3B; Table S3).
Figure 3. Pleiotropy underlies the fitness effect of gene knockout across human cancer cell lines.
(A) The Cancer Dependency Map (DepMap) fitness screen collection. Individual human cancer cell lines were screened for genetic dependencies for cell growth by comparing cell counts before and after infection with a genome-scale CRISPR-Cas9 gene knockout library.
(B) The DepMap data were preprocessed to a set of 2,921 high-variance fitness genes screened across 675 cell lines. From this data alone, Webster learned a dictionary matrix of 220 fitness effects reflecting inferred biological functions and approximated each gene effect in terms of four functional effects.
(C) Webster approximated the fitness effect of SHOC2 knockout as a mixture of four functional effects (activated KRAS, activated NRAS, EGFR signaling, and FGFR signaling), each of which were strongest in cell lines harboring corresponding genomic alterations (KRAS mutation, NRAS mutation, activated EGFR, and FGFR expression, respectively). This decomposition reflects the pleiotropic interactions underlying SHOC2’s overall function downstream of these signaling pathways.
(D) Joint UMAP embedding of fitness effects for genes and functions inferred from DepMap data. Each of the 220 functions (triangles) and 2,921 genes (circles) are co-embedded in a 2D layout. Selected functions of interest are labeled on the map. Gene effect data from Cancer Dependency Map 19Q4v3 release (https://doi.org/10.6084/m9.figshare.11384241.v3). Functional effects inferred with Webster (this study).
(E) For each function from (C), genes in the joint embeddings are colored according to their loadings on each function, including an inset focusing in on the immediate neighborhood of the function of interest. To the right, the top 10 ranked genes are shown with a heatmap of their respective gene loadings. Gene effect data from Cancer Dependency Map 19Q4v3 release (https://doi.org/10.6084/m9.figshare.11384241.v3). Functional effects inferred with Webster (this study).
(F) Top: relationships learned from fitness data for SHOC2 and RAF1, which also acts downstream of activated RAS proteins. Each arrow corresponds to an inferred gene-to-function loading. Bottom: Illustration of SHOC2/RAF1’s shared biological role in activated RAS signaling.
(G) A network of SHOC2-related functions. Each node is a function inferred by Webster from fitness data. Pleiotropic genes with loadings on two functions are plotted as edges in the network, with the number of pleiotropic genes connecting functions represented by the line thickness. The four bolded functions are those used in the SHOC2 gene effect approximation, while the three additional functions shared at least two pleiotropic genes with one of these four functions.
We further validated that Webster was robust to noise (Figure S3C), reproducible across random runs over identical parameters (Figure S3D), and that dictionaries trained on one cancer fitness dataset could successfully model perturbations from another dataset performed with a different CRISPR-Cas9 guide library and cell culture conditions (Behan et al., 2019) (Figure S3E). Dictionary elements learned at our chosen hyperparameters (k = 220, t = 4) were robustly learned across other hyperparameter settings; in particular, learning dictionaries at lower values of k resulted in subsets of our 220-element dictionary (Figure S3F; Table S3).
We matched each dictionary element to a biological function by annotating the strongest loaded genes, supported by consensus cell line features that explain the fitness effect captured by the element. Ninety percent of dictionary elements captured the fitness effect of losing literature-supported functions, whereas the remaining elements captured technical factors such as common essential effects (Table S3).
Webster modeled gene effects as mixtures of functional effects learned empirically from the data. For instance, SHOC2 is part of the oncogenic RAS signaling pathway. Webster approximated the effect of SHOC2 depletion in 675 cell lines in terms of four functional effects (Pearson cor = 0.85, Figure 3C):
Cell lines with the strongest fitness effects per function exhibited matched molecular alterations: KRAS hotspot mutations, NRAS hotspot mutations, activated EGFR, and high FGF expression, respectively (Figures 3C and S3G). These genomics features were unused during model training. By looking globally across fitness data alone, Webster discovered cell contexts with distinct activated signaling pathways that influence SHOC2 function.
We charted a landscape of cancer cell fitness by jointly embedding 2,921 genes and 220 functions according to their fitness effects using UMAP (Figure 3D; Table S4). For biological processes such as oxidative phosphorylation, mitotic chromosome separation, cytoskeleton, and epigenetic regulation, Webster resolved distinct protein complexes or functional units within that process (Figure 3D).
Within cancer signaling, RAF1 is another obligate RAS effector whose gene effect was a mixture of activated NRAS and activated KRAS, as reflected by the UMAP embedding (Figure 3E) and loadings (Figure 3F). GRB2 and PTPN11 are effectors of growth factor signaling whose gene effects were mixtures of EGFR signaling and FGFR signaling, as reflected in their embeddings (Figure 3E). Other genes such as BRAF, MAPK1, DOCK5, and CRKL spanned-related pathways such as BRAF signaling and focal adhesion, forming an interaction network between genes and inferred functional effects (Figure 3G).
Half of the gene effects that were well approximated by Webster (Pearson cor ≥ 0.4) exhibited evidence of multifunctionality (loadings ≥ 0.25 SD on at least two functions), suggesting that cancer cell fitness obeys more complex genetic architectures than previously appreciated and places cancer cells in line with other model organisms where a majority of genes exhibit pleiotropy (Wang et al., 2010).
Modeling genes as compositions of functions extends pairwise gene similarity approaches
An important distinction exists between our sparse approximation models and pairwise guilt-by-association correlations commonly applied to this type of data (Amici et al., 2021; Bayraktar et al., 2020; Boyle et al., 2018; Kim et al., 2019; Pan et al., 2018; Wainberg et al., 2021). The measured fitness effect of SHOC2 correlates strongly with that of RAF1 (Pearson = 0.64) but weakly with RAS proteins themselves (NRAS, Pearson cor = 0.29, KRAS, cor = 0.26). Despite being highly related genes, NRAS and KRAS fitness effects are in fact anti-correlated (Pearson cor = −0.17) because their activating mutations occur in mutually exclusive cell lines. This presents a paradox that guilt-by-association approaches alone fail to solve, instead requiring supervised learning approaches with cell line mutation data as input (Kim et al., 2021).
Webster’s approach returned unsupervised representations of biological functions from fitness data alone, which included activated NRAS and activated KRAS. Composing these functions together allows the model to represent complementary paths to SHOC2 dependency. Indeed, the simplified expression
achieves a higher pairwise correlation with SHOC2 fitness effect than any single gene in the original data (Pearson cor = 0.81).
A second limitation of pairwise similarity metrics is that negative correlations are typically elided from the data before clustering or visualization. In our model, a negative regulator of a function can be modeled with a negative loading, indicating its knockout has the opposite effect from a positive regulator. As an example, KRAS is inhibited by NF1 and degraded by LZTR1; both genes have negative loadings on the Activated KRAS function (−0.5 for NF1 and −0.4 for LZTR1).
Modular pleiotropy underlies the fitness effect of protein complexes
Pleiotropy has a modular structure, such that groups of collaborating genes share pleiotropic functions (Wagner and Zhang, 2011). A biochemical basis for modular pleiotropy arises when protein complexes share common subunits yet perform distinct functions. The enzymatic module consisting of SGF29, KAT2A, and TADA3 is shared by the STAGA and ATAC complexes (Figure 4A) (Spedale et al., 2012). From the fitness data alone, Webster learned independent functions for STAGA and ATAC complexes and parsimoniously represented the effect of perturbing shared subunits as
Figure 4. Modular pleiotropy within protein complexes resolves C7orf26 as a member of the Integrator complex INTS10–13-14 module.
(A) STAGA and ATAC protein complexes share a histone acetyltransferase module. From cancer cell fitness data alone, Webster inferred separate functional effects of STAGA and ATAC depletion while decomposing the effect of knocking out shared subunits as a mixture of STAGA and ATAC depletion.
(B) The SWI/SNF family protein complexes consist of specialized subunits bound to the common enzymatic subunit SMARCA4. From cancer cell fitness data alone, Webster inferred separate functional effects of depleting each subcomplex while decomposing the effect of SMARCA4 knockout as affecting all three subcomplexes.
(C) The Integrator complex is a modular RNA endonuclease complex. From cancer cell fitness data alone, Webster learned three distinct functional effects involving Integrator complex componentry. Each of the three functions captured the specific effect of knocking out recently discovered structural modules of the complex. An unknown interactor, C7orf26, was approximated as a mixture of all three Integrator functions, with the strongest loaded function mapping to the INTS10–13-14 functional module.
(D) Schematic of two C7orf26 gene splice variants curated by the genotype-tissue expression (GTEx) portal.
(E) Immunoprecipitation (IP) of C7orf26-HA variants from 293T nuclear extracts, immunoblotted for INTS10–13-14 module subunits.
(F) Mass spectrometry of C7orf26-HA and C7orf26-V5 immunoprecipitations from 293T cells shows stoichiometric pull down of INTS10, 13, and 14 with the full-length C7orf26.
(G) 293T cells with CRISPR-Cas9 perturbation of C7orf26 display loss of INTS10 at the protein level.
(H) IP of endogenous C7orf26 from 293T cells with and without INTS10 knockout.
(I) Model figure—C7orf26 stabilizes INTS10, which assembles together with the INTS13–14 heterodimer to form the INTS10–13-14-C7orf26 module.
In contrast, two protein paralogs ADA2A and ADA2B have similar sequences (45% positive alignment in BLAST) but exclusively bind ATAC and STAGA, respectively. Their effects are approximated as
The remaining STAGA and ATAC subunits also follow this pattern (Figure S4A).
SWI/SNF is a family of three chromatin remodeling complexes:: ncBAF, cBAF, and pBAF. Each complex shares the enzymatic subunit SMARCA4 (Mashtalir et al., 2018) (Figures 4B and S4B). Webster decomposed the effect of SMARCA4 knockout as follows:
ARID1A exclusively binds cBAF, while BRD9 and BRD7 are paralogous proteins that exclusively bind ncBAF and PBAF, respectively. Their fitness effects were encoded as follows:
The ancestral BRD7/9 protein in Drosophila binds both pBAF and ncBAF (Barish et al., 2020), but gene duplication evolved two specialized mammalian paralogs that exclusively function in one or the other complex (Michel et al., 2018). Our ability to infer different functions for paralogs (ADA2A/B and BRD7/9) based on differing fitness contexts evokes the “semantic change” of words inferred from differing sentence contexts over time (Boleda, 2020).
As a final example, Webster recovered two distinct functions involving the Mediator complex, with head module subunits mapping to one and Tail/CKM module subunits mapping to the other, consistent with patterns previously observed in cancer fitness data (Boyle et al., 2018; Pan et al., 2018) (Figure S3C).
Modular pleiotropy in the Integrator complex
The Integrator protein complex localizes to the nucleus and exhibits RNA endonuclease activity (Baillat and Wagner, 2015) but is incompletely characterized. From the fitness data alone, Webster resolved three distinct functions corresponding to recently discovered biochemical modules (Figures 4C and S3D). One fitness effect is specific to the backbone and shoulder modules (Zheng et al., 2020), with the top-loaded genes being INTS6, INTS12, INTS5, INTS7, and INTS8. Components of the RNA Pol II transcriptional pausing machinery were also loaded onto this function (HEXIM, LEO1, and WDR61), suggesting this fitness effect is partially explained by the signal-dependent role of Integrator in transcriptional pause/release (Elrod et al., 2019; Gardini et al., 2014; Hou et al., 2019; Stadelmayer et al., 2014; Tatomer et al., 2019). A second function mapped to the recently characterized interaction between WDR73 and the endonuclease module (Tilley et al., 2021). WDR73 was the strongest loaded gene (1.8), followed by BRAT1 (1.5) and INTS9 (0.7).
Finally, Webster inferred the fitness effect of perturbing the INTS10–13-14 heterotrimer, a physical and functional module of the Integrator complex (Barbieri et al., 2018; Mascibroda et al., 2020; Pfleiderer and Galej, 2021; Sabath et al., 2020). INTS10, INTS14, and INTS13 were the strongest loadings on this function (1.1, 0.9, 0.8, respectively), along with a fourth gene, C7orf26 (1.0).
C7orf26 stabilizes INTS10 as a member of the Integrator complex INTS10–13-14 module
The conserved C7orf26 protein consists of a single domain of the unknown function (DUF4507) and has been nominated as a putative Integrator interactor in proteomic datasets (Baillat et al., 2016; Boeing et al., 2016; Drew et al., 2020; Malovannaya et al., 2010) although the nature of its relationship to Integrator is not understood. Webster modeled the fitness effect of C7orf26 perturbation as a mixture of all three Integrator functions defined above:
with two-thirds of its overall fitness effect explained by the INTS10–13-14 module. To investigate this observation further, we exogenously expressed HA-tagged versions of two C7orf26 isoforms in human 293T cells (Figure 4D). Using immunoprecipitation, we observed a robust interaction between the full-length C7orf26 protein and INTS10, 13, and 14 (Figures 4E and S4E). These interactions were not observed for the shorter C7orf26 isoform (Figure 4E), suggesting the two missing DUF4507 microdomains (Figure 4D) were necessary for the interaction. Upscaling our biochemical purifications and subjecting eluted material to mass spectrometry, we identified stoichiometric amounts of INTS10, 13, and 14 with full-length C7orf26 pull-down (Figure 4F; Table S5). The INTS9–4-11 endonuclease module subunits were also present but at lower levels, followed by the remaining Integrator subunits. As before, the shorter isoform failed to pull down INTS10, INTS13, or INTS14 (Figure 4F).
To interrogate the biochemical mechanism of C7orf26’s role in the INTS10–13-14 module, we generated C7orf26 knockout 293T cells and assessed the protein abundance of other Integrator subunits. Compared to control cells, loss of C7orf26 abrogated INTS10 protein levels (Figures 4G and S4F) while sparing other Integrator subunits, including INTS13 and 14 (Figure 4G). In the reciprocal INTS10 knockout, we observed that C7orf26 protein levels remained constant, but endogenous C7orf26 failed to bind INTS13 in the absence of INTS10 (Figure 4H).
These observations indicate C7orf26 nucleates the assembly of INTS10 with the INTS13–14 heterodimer (Sabath et al., 2020), resulting in a INTS10–13-14-C7orf26 heterotetrameric module of the Integrator complex (Figure 4I). This assembly chain was supported by co-sedimentation patterns of native nuclear extracts, in which C7orf26 existed as a monomer at low molecular weights but co-eluted with INTS10 at higher molecular weights characteristic of the full complex (Figure S4G). In previous in vitro purification efforts from insect cells, INTS10 was unstable when expressed in isolation (Sabath et al., 2020); adding C7orf26 to these preparations may stabilize INTS10. Previous guilt-by-association studies assigned C7orf26 to a large gene cluster containing the union of all three Integrator modules (Wainberg et al., 2021), thereby eliding the underlying pleiotropic interactions reflecting its specific stoichiometry within the complex.
Learned functions reflected a cellular hierarchy
Next, we explored the properties of the latent space defined by Webster’s functions. Gene products are spatially regulated within a cellular hierarchy (Figure 3D), but because Webster is trained on fitness data alone, it has no prior knowledge of this hierarchy (Figure 5A). We leveraged recently published proximity labeling measurements (Go et al., 2021) represented as probability distributions for each gene product over 20 subcellular locations. By multiplying gene location probabilities with our gene-to-function loadings, we computed scores indicating the level of physical compartmentalization for each fitness function (Figure S5A; Table S6).
Figure 5. Gene function embeddings reflect pleiotropy between hierarchically compartmentalized functions.
(A) Conceptual overview of cellular organization. After learning gene functions with Webster from cancer fitness data alone, experimentally derived subcellular localization data (Go et al., 2021) were used to annotate Webster’s functions across 20 subcellular locations within a total of 7 cellular compartments.
(B) Joint embedding of fitness effects for genes and functions inferred from DepMap data, with functions colored by their specificity for one of seven cellular compartments—mitochondria, endoplasmic reticulum (ER), recycling, membrane, nucleus, cytosol, and miscellaneous. Subcellular location data were not used during the training of the Webster model. Gene effect data from Cancer Dependency Map 19Q4v3 release (https://doi.org/10.6084/m9.figshare.11384241.v3). Functional effects inferred with Webster (this study). Subcellular location data from Human Cell Map (Go et al., 2021).
(C) Insets from (B). detailing functions within the ER, recycling and membrane compartments, capturing specific subcellular locations or protein complexes within these broad compartments. Gene effect data from Cancer Dependency Map 19Q4v3 release (https://doi.org/10.6084/m9.figshare.11384241.v3). Functional effects inferred with Webster (this study). Subcellular location data from Human Cell Map (Go et al., 2021).
(D) Insets from (C). detailing genes embedded nearby their pleiotropic gene functions. Bolded genes are mentioned in the main text. Gene effect data from Cancer Dependency Map 19Q4v3 release (https://doi.org/10.6084/m9.figshare.11384241.v3). Functional effects inferred with Webster (this study). Subcellular location data from Human Cell Map (Go et al., 2021).
(E) Pleiotropic genes bridge biological functions that are physically distinct. Left: Pleiotropic genes for peroxisome biogenesis and cholesterol biosynthesis functions, which are enriched at the peroxisome and the ER, respectively. Middle: Pleiotropic genes for the Commander/WASH, HOPS/CORVET, and amino acid activation of mTOR functions, which are enriched at the early endosome, endosomal vesicles, and lysosomes, respectively. Right: Pleiotropic genes for the SCAR/WAVE (cytosol), integrins, and focal adhesion functions.
Grouping the 20 fine-grained locations by physical or functional similarity resulted in seven coarse-grained compartments: nucleus, endoplasmic reticulum (ER), recycling, cytosol, mitochondria, membrane, and miscellaneous (ribosomes and other large protein complexes) (Figure S5B). Functions enriched for specific compartments incurred similar fitness effects and occupied nearby regions of the embedding space (Figures 5B, S5C, and S5D). Individual functions reflected subcellular locations such as the ER lumen, the outer nuclear membrane, and peroxisome within the coarse-grained ER compartment; additional examples included lysosome and retrograde transport functions within the recycling compartment and focal adhesions and cell junction functions within the membrane compartment (Figure 5C).
Certain gene effects were modeled as mixtures of functions spanning distinct (but related) subcellular locations. In Webster, the effect of perturbing the C12orf49 gene was approximated as
reflecting its recently characterized role in sterol biosynthesis at the ER membrane (Aregger et al., 2020; Bayraktar et al., 2020; Loregger et al., 2020; Xiao et al., 2021), the metabolites for which are delivered to the ER by peroxisomes (Costello et al., 2017; Hua et al., 2017). Additional pleiotropic genes spanned these differentially localized functions (Figure 5E).
As another example, the effect of perturbing VPS39 was approximated in Webster as
VPS39 is a HOPS complex member that endosomally recycles proteins with CORVET. The HOPS complex was recently implicated in mTOR activation via lysosomally recycled amino acids (Hesketh et al., 2020). The strongest loaded genes on the amino acid activation of mTOR function are Ragulator, Rag, Folliculin, and GATOR2 complex members (all localized to the lysosome), HOPS complex members (localized to endosomes), as well as mTOR itself. Additional pleiotropic genes spanned these differentially localized functions (Figure 5E).
These results echo other biological hierarchies observed in fitness data from organisms such as yeast (Costanzo et al., 2016; Kramer et al., 2014). Most gene functions were either indirectly or unrelated to cancer biology at large, suggesting that drivers of cancer pathology exert second-order effects on normal physiological pathways across cell lines. Finally, these hierarchical relationships are largely absent when mapping the 220 functional effects alone (Figure S5E) because dictionary elements themselves are decorrelated by design. To facilitate exploration of the Webster’s analysis of cell fitness data, we provide an interactive portal for exploring pleiotropic gene relationships (http://depmap.org/webster/).
Projecting compounds into a latent space defined by gene functions
The PRISM Drug Repurposing dataset contains compound sensitivity measurements across hundreds of cancer cell lines (Corsello et al., 2020). These compound sensitivity measurements were unseen during dictionary learning on gene perturbation data (Figure 3B). We assessed whether this dictionary optimized on gene perturbation data captured patterns present in compound sensitivity data (Figure 6A). To do this, we isolated ~200 compounds with diverse and well-annotated mechanisms of action from the PRISM dataset and modeled each compound sensitivity profile as a mixture of four elements of the dictionary trained exclusively on gene perturbation data (Figure 6B; Table S7). The better the approximations, the greater the generalizability of our approach, indicating that Webster’s latent functions captured true biology (as opposed to dataset-specific effects).
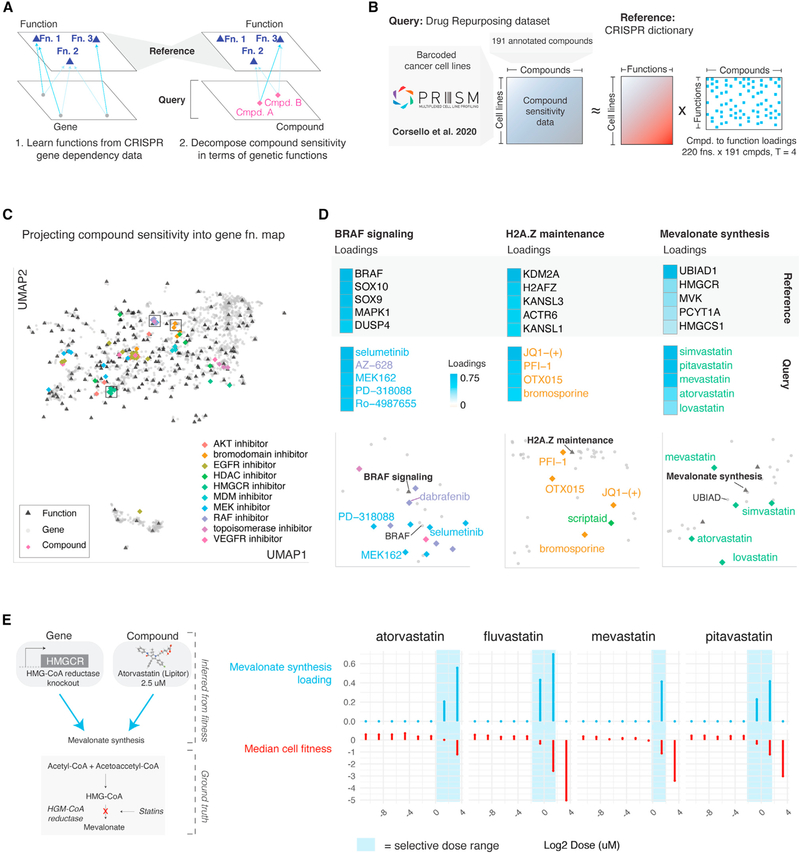
Figure 6. Projecting compound perturbations into a reference space of gene functions.
(A) Conceptual overview of reference-query projection for fitness data. If Webster learned true biological functions from gene perturbation data, those functions should generalize to unseen perturbations measured over the same cell lines, such as compound sensitivity measurements.
(B) Overview of query dataset. Compounds from the Drug Repurposing Hub were screened at a uniform dose (2.5 μM) over a set of barcoded cell lines to generate compound sensitivity profiles (Corsello et al., 2020). We modeled 191 high-variance compound treatments by approximating each compound sensitivity profile as a mixture of up to four gene functions learned from CRISPR data using Webster. Compound data were not used during the training of the gene function dictionary.
(C) Joint UMAP embedding of genes, functions, and compound sensitivity profiles. Compounds embedded near gene functions reflecting their mechanism of action. Gene effect data from Cancer Dependency Map 19Q4v3 release (https://doi.org/10.6084/m9.figshare.11384241.v3). Functional effects inferred with Webster (this study). Compound sensitivity data from PRISM Drug Repurposing 19Q4v4 Dataset (https://doi.org/10.6084/m9.figshare.9393293.v4).
(D) Focus on three gene functions: BRAF signaling, H2A.Z maintenance, and mevalonate synthesis. Top: The five genes most strongly loaded onto each function are shown next to a heatmap of their loading scores. Middle: The compounds most strongly loaded onto each gene function are shown next to a heatmap of their loading scores. Bottom: Insets of the embedding shown in (C) centered on each of the three gene functions.
(E) Query compound projection onto reference gene functions varies by dose. In a secondary screen, various HMGCR inhibitors were screened at an 8-point dose curve ranging from 10 μM to 8 nM. Compound sensitivity profiles at each dose point were modeled independently in terms of Webster’s gene functions. The resulting loadings on the mevalonate synthesis function are plotted against the dose (see also Figure S6E).
Approximation quality of compound sensitivity using gene functions varied by compound class (Figure S6A), with clinical anticancer compounds such as MDM and EGFR inhibitors exhibiting the best approximations, and broadly cytotoxic compounds such as aurora kinase inhibitors exhibiting the least robust approximations (Figure S6B). Well-approximated profiles projected onto genetically defined pathways that reflected compound mechanism of action (Figure 6C). As examples, RAF and MEK inhibitors treatment profiles projected onto the BRAF signaling function, whose fitness effect is strongest in BRAF mutant melanomas (Figure S6C). The strongest loaded genes on this function are BRAF, SOX10, SOX9, MAPK1, and DUSP4; the strongest loaded compounds included selumetinib and AZ-628 (Figure 6D). Similarly, bromodomain inhibitors projected onto the H2A.Z maintenance function, while HMGCR inhibitors projected onto the mevalonate synthesis function (Figure 6D). These observations suggested that Webster learned representations of on-target pathways for certain compound classes from gene perturbation data alone, in concordance with previous results on pairwise gene-drug correlations (Gonçalves et al., 2020).
Moreover, some profiles were modeled as interpretable mixtures of multiple independent biological pathways. For example, ATK inhibitor sensitivity profiles were modeled as mixtures of RICTOR/AKT signaling, PIK3CA signaling, and PTEN signaling functions (Figure S6D). Furthermore, we found that projection onto on-target pathways was sensitive to compound dose. From a secondary PRISM dataset in which compound sensitivity was measured at an eight-point dose curve, we observed selective dose ranges for specific compounds. Compound doses within these ranges resulted in sensitivity profiles with strong loading scores on their on-target functions, while high doses that caused broad cytotoxicity or low doses with no fitness effect failed to project at all (Figures 6F and S6E).
DISCUSSION
Wagner and Zhang nominated pleiotropic inference as an outstanding problem in functional genomics a decade ago (Wagner and Zhang, 2011), envisioning two major challenges: deriving “biologically nonarbitrary” latent phenotypes from high-dimensional data and accounting for the sparse nature of genotype-phenotype relationships (Wang et al., 2010). By framing pleiotropy as an instance of the sparse representation problem (Elad, 2010) solved by graph-regularized dictionary learning, we recovered interpretable latent dictionary elements that sparsely combine to model gene effects, thereby satisfying the two challenges outlined above. Webster meets the analytical challenge posed by growing CRISPR-Cas9 fitness screens by enabling unsupervised learning of biological functions using only numerical fitness data as input. It is generally applicable to fitness screen collections of various designs and may be especially useful in organisms in which fitness screens are experimentally tractable but gene functions are poorly annotated, such as bacteria (Price et al., 2018). Future work could address limitations of our current method, for instance, by regularizing on hierarchical graph structures rather than simple neighbor graphs or by learning the degree of pleiotropy as a per-gene parameter rather than setting it globally.
We anticipate that the future application of Webster to growing fitness screen collections, enabled by our open-sourced implementation (STAR Methods), will resolve context-specific functions that are difficult to perceive when studying individual experimental models. Proteins that exhibit different functions in specific contexts are often difficult to resolve using single experimental models, and current practice is to reproduce experiments in multiple cell lines or models. This approach is experimentally sound but may obscure essential biochemical interactions that more accurately inform biological insights.
Furthermore, the dictionary framework created by Webster allows one to infer function by projection. We demonstrated that analyzing cell fitness data from a large panel of small molecules with at least one known target allowed us to infer the biological pathways perturbed by specific molecules and identify compounds with generalized fitness effects. The use of Webster to analyze biologically active small molecules may provide a method to rapidly identify the targets of novel small molecules and accelerate drug discovery.
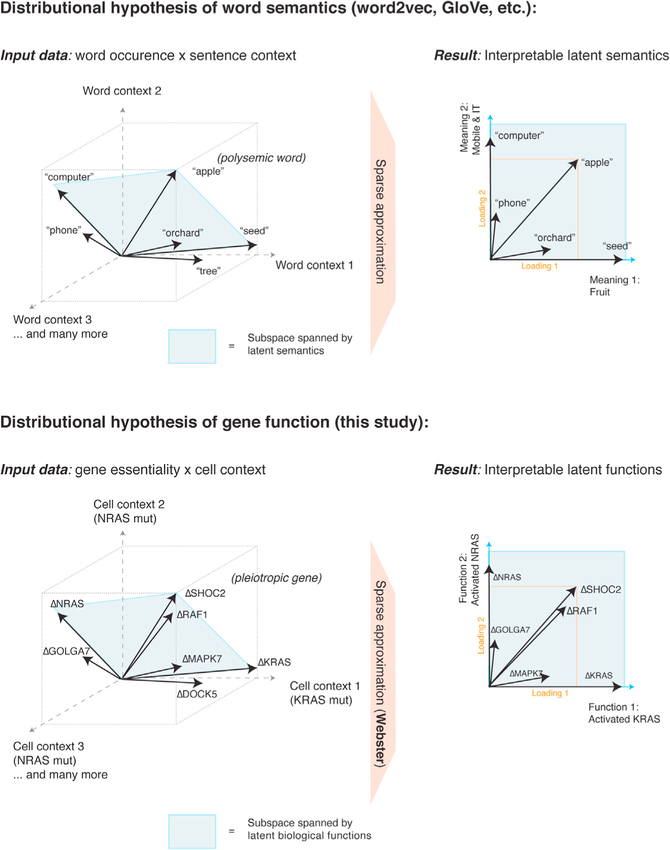
Representing gene effects as vectors distributed over a space of latent functions runs counter to traditional symbolic representations (e.g., gene A performs function B if condition C is satisfied) (Fraser and Marcotte, 2004; Norman et al., 2019). However, in natural language processing, word symbols are represented as vectors distributed over a space of latent semantics (Mikolov et al., 2013; Pennington et al., 2014). Dictionary learning applied to word vectors (word2Vec and GloVe) resolves polysemic words as sparse linear combinations of latent meanings, such as “apple” ≈ 0.16 × fruit + 0.22 × mobile phone + … (Zhang et al., 2019)
The fact that polysemic words and pleiotropic genes are modeled by dictionary learning suggests that word co-occurrence and gene co-fitness share statistical regularities. Perhaps the distributional hypothesis of semantics (you shall know a word by the company it keeps) (Boleda, 2020) also applies to gene function (you shall know a gene by shared causal effects with other genes). If so, it may be advantageous to transition from genotype-phenotype “maps” to “geometries,” where statistically independent phenotypes form an empirically derived latent space in which gene effects are vectors (Figure 7) (Fischer et al., 2015).
Figure 7. A distributional hypothesis of gene function.
Distributional semantics powers modern advances in machine learning applied to natural language. These models rely on latent spaces derived from word co-occurrence statistics. Representing a word as a vector in this space enables numerical reasoning about word meanings. In particular, applying sparse dictionary learning to word vectors recovers interpretable semantics, capturing polysemy. Similarly, gene effects may be thought of as vectors as well, defined by essentiality measures across cell contexts. Webster discovers latent functions that “point” in the direction of strongly co-essential fitness genes. Pleiotropic genes can then be modeled as mixtures of these latent functions.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, William Hahn (William_Hahn@dfci.harvard.edu).
Materials availability
Plasmids generated in this study have been deposited to Addgene.
Data and code availability
This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table. All other data reported in this paper will be shared by the lead contact upon request.
Key resources table.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| HA | Cell Signaling Technology | 2367S |
| INTS10 | Abcam | ab180934 |
| C7orf26 | Novus | NBP2-14764 |
| INTS13 | Bethyl | A303-575A |
| INTS14 | Bethyl | A303-576A |
| INTS9 | Cell Signaling Technology | 13945S |
| INTS6 | Santa Cruz | sc-376524 |
| TBP | Abcam | ab51841 |
| Deposited data | ||
| Genotoxic fitness screens | http://durocherlab.org/datasets/ | https://doi.org/10.1016/j.cell.2020.05.040, Supplementary Table 2 |
| Cancer Dependency Map, 19Q4 release (fitness data for Webster input) | https://depmap.org/portal/ | https://doi.org/10.6084/m9.figshare.11384241.v3 |
| Cancer Dependency Map, 21Q2 release (omics data for biomarker pipeline) | https://depmap.org/portal/ | https://doi.org/10.6084/m9.figshare.14541774.v2 |
| PRISM Drug Repurposing data | https://doi.org/10.1038/s43018-019-0018-6 | https://doi.org/10.6084/m9.figshare.9393293.v4 |
| Human Cell Map (proximity ligation data) | 10.1038/s41586-021-03592-2 | 10.1038/s41586-021-03592-2 |
| Experimental models: Cell lines | ||
| 293FT | Thermo Fisher Scientific | R70007 |
| Oligonucleotides | ||
| INTS6 Avana gRNA (chr13_51452485_+): ATGGCTGCGCTGGTTCATAG | This paper | N/A |
| INTS10 Avana gRNA (chr8_19823975_−) : TCTTAAACAACCTCTCCCAA | This paper | N/A |
| C7orf26 Avana gRNA (chr7_6594465_+) : TTACTGTGTGAGGTTAGCCA | This paper | N/A |
| Recombinant DNA | ||
| lentiCRISPR v2-Blast | Addgene | 83480 |
| pLEX_307 | Addgene | 41392 |
| pLX_HA | This study | 178534 |
| pLX_HA-C7orf26v1 | This study | 178535 |
| pLX_HA-C7orf26v2 | This study | 178536 |
| pLX_317-C7orf26v1 | This study | 178537 |
| pLX_317-C7orf26v2 | This study | 178538 |
| Software and algorithms | ||
| R | R Foundation | https://www.r-project.org/ |
| MATLAB | Mathworks | https://www.mathworks.com/products/matlab.html |
| gProfiler | doi:10.1093/nar/gkz369 | https://biit.cs.ut.ee/gprofiler/ |
| DGRDL | 10.1109/TSIPN.2016.2605763 | https://elad.cs.technion.ac.il/software/ |
| gene_fn | This study | 10.5281/zenodo.5773076 |
| graph_dictionary_learning | Various open source codebases | 10.5281/zenodo.5773078 |
All original code has been deposited and is publicly available as of the date of publication. The main repository contains R code for reproducing figures and analyses presented in the paper and can be found at https://github.com/joshbiology/gene_fn (Zenodo archive: https://doi.org/10.5281/zenodo.5773076). We created a Figshare archive that is the starting point for these analyses (https://doi.org/10.6084/m9.figshare.14960006.v2). We provide a second repository of MATLAB code implementing the factorization methods that are the basis of Webster, which can be found at https://github.com/joshbiology/graph_dictionary_learning (Zenodo archive: https://doi.org/10.5281/zenodo.5773078). Finally, we provide a data repository containing Webster’s preprocessed numerical input data and subsequent analysis output, a subset of which form the Supplemental Tables cited throughout this paper (https://doi.org/10.6084/m9.figshare.14963561.v2).
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
The female-derived 293T cell line was obtained from Thermo Fisher Scientific (R70007, under the product name 293FT) and grown in DMEM (Thermo Fisher Scientific, 12430054) supplemented with 2 mM glutamine, 50 U/mL penicillin, 50 U/mL of streptomycin (Gibco), and 10% fetal bovine serum (Sigma).
METHOD DETAILS
Overview of the sparse approximation problem
The field of sparse approximation encompasses a diverse range of applications and implementation strategies. One specific formulation of the sparse approximation problem is centered around the following task (from (Elad, 2010), “Chapter 9.2 The Sparse-Land Model”, see also (Yankelevsky and Elad, 2016), “I. Introduction” and (Mairal et al., 2014), “Chapter 1.4 Dictionary Learning”):
Suppose a set of m training signals Y = [y1, y2, …, ym] in Rn (indicating that each yi is an n-dimensional vector of real numbered values). From this set of training signals alone, we seek to approximate them by recovering:
A dictionary matrix D in Rn×k (indicating that D is a matrix of real numbered values with n rows and k columns)
Sparse representations of each training signal in terms of dictionary elements. These representations form a matrix X = [x1, x2, …, xm] with each xi being a t-sparse vector in Rk (indicating that xi is a k-dimensional vector with all but t entries set to 0).
The approximation of each training signal is yi ≈ D* xi. The term on the left is the measured signal, which is a vector in Rn. The term on the right is a matrix operation resulting in a vector in Rn, composed from the weighted sum of t columns of D (each of which are vectors in Rn), with the weights being the t non-zero coefficients held in xi.
We can also express this in matrix form:
To solve the sparse approximation problem, we find an optimal solution to both D and X that minimizes the approximation error, given the sparsity constraints imposed by the parameter t, and the number of dictionary elements dictated by k. Formally, the objective is
Sparse approximation of pleiotropic gene functions from fitness data
We adapt the framework of sparse approximation to model fitness data. Fitness data consists of measured changes in cell growth rate upon biological perturbations applied across cell contexts. Here, we focus on gene perturbation, which can be induced in a variety of ways, including with programmable CRISPR-Cas9 nucleases. For additional descriptions of fitness experiments and their designs, see (Rancati et al., 2018) (focused on human cells) and (Costanzo et al., 2019) (focused primarily on yeast).
We are specifically interested in modeling the genetic architecture underlying fitness measurements. In particular, we seek to model pleiotropy, in which gene products have multiple functions depending on the cell context. Solving pleiotropy within fitness data reduces to (1) learning a set of fitness effects of perturbed biological functions, and (2) modeling gene effects as a combination of these functional effects.
There is a clear connection between these two tasks and the basic sparse approximation problem described above, although augmentations are required to encourage latent dictionary elements to model biological functions rather than numerically valid – but biologically meaningless – patterns in the data. To achieve this, we exploit several properties of fitness data. First, genes with correlated fitness effects tend to have similar biological functions, a concept referred to as co-essentiality (Amici et al., 2021; Bayraktar et al., 2020; Boyle et al., 2018; Kim et al., 2019; Pan et al., 2018; Wainberg et al., 2021; Wang et al., 2017). Second, similar cell contexts will share similar rate-limiting functions for cell growth. This concept has been most extensively explored in the cancer field, in which related cell lines have been shown to harbor similar “selective dependencies” (McDonald et al., 2017; Tsherniak et al., 2017). Constraining learned representations to capture coherent gene modules essential in specific cell contexts is consistent with past use of bi-clustering to model pleiotropy (Dudley et al., 2005; Koch et al., 2017).
In summary, to recover latent representations in our model that capture biological functions, we augmented the basic sparse approximation objective (error minimization) with two additional objectives: learned representations should preserve the local structure between gene effects as well as preserve the local structure between cell contexts. To operationalize this, we adopted the framework of dual-graph regularized dictionary learning.
Webster: Dual graph regularized dictionary learning applied to preprocessed fitness data
Our overall approach (Webster) for modeling pleiotropic gene functions in fitness data consists of two steps. First, we preprocess the fitness data. This is done by centering and scaling individual screens, then centering the fitness effects of each gene perturbation (‘gene effects’), and finally filtering out low variance gene effects. Batch correction and other quality control steps are applied at this stage as well, described in detail in later sections. Second, from this matrix of preprocessed gene effects, Webster uses dual graph regularized dictionary learning (DGRDL) (Yankelevsky and Elad, 2016, 2020) to sparsely approximate the gene effect matrix in terms of latent biological functions.
Mathematically, this can be described as follows. Let the set of gene effects Y = [y1, y2, …, ym] in Rn consist of fitness effects upon individually perturbing m genes across n cell contexts. Pairwise similarities between the m gene effects define a matrix W in Rm×m, while the pairwise similarities between the n cell contexts define a matrix V in Rn×n.
From Y, W and V, we recover a dictionary matrix D in Rn×k and a sparse representation matrix X in Rk×m (with each column of X containing only t non-zero entries). D and X are optimized to satisfy the following objectives:
Minimize the total approximation error ‖ Y − D * X ‖F (indicating the Frobenius norm of the difference between the original gene effect matrix and the approximated gene effect matrix);
Minimize the sum of squared differences between the columns of X, weighted by the similarities of the corresponding columns of Y, expressed as , for all i and j between 1 and m;
Minimize the sum of squared differences between the rows of D, weighted by the similarities of the corresponding rows of Y, expressed as , for all i and j between 1 and n.
The intuition behind objective (2) is that the more similar two gene effects are in the original data, the more similar their sparse representations should be; i.e. they should be approximated using similar biological functions. The intuition behind objective (3) is that the more similar two cell contexts are in their growth requirements, the more similar their representations in the dictionary matrix should be, i.e they should depend on the same functions for growth. Formally, objectives (2) and (3) can be compactly expressed as a quadratic form of a graph Laplacian derived from the gene effect similarity graph and the cell context similarity graph, respectively.
The final DGRDL objective function is:
where L in Rm×m is the Laplacian matrix derived from the cell context similarity graph, Lc in Rn×n is the Laplacian of the gene effect similarity graph, and α and β are importance weights for each term in the final objective. In practice, we choose k < m, as we assume that gene effects can be described by a small set of latent elements. We also tend to choose k < n, resulting in an undercomplete dictionary basis. Finally, we choose t to be small (t ≪ k) but greater than 1.
This is a high-level summary of DGRDL specifically through the lens of fitness data. For a fuller exploration of DGRDL applied to other data modalities, as well as theoretical guarantees of DGRDL for signal recovery, see the original papers: (Yankelevsky and Elad, 2016, 2020).
Implementation details
In order to implement DGRDL, we obtained MATLAB code for k-SVD, orthogonal matching pursuit, and DGRDL from the respective lab websites (https://elad.cs.technion.ac.il/software/ and http://www.cs.technion.ac.il/~ronrubin/software.html), which we detailed in the documentation for our code repository (https://github.com/joshbiology/graph_dictionary_learning).
Our Webster approach customizes the base DGRDL method in several ways. First, we use nearest-neighbor graphs in our graph regularization terms, with the goal of preserving local structure present in the data. Empirically, nearest neighbor graphs capture the overall topological relationships present in gene effect similarity networks (Amici et al., 2021; Pan et al., 2018), and provide the highest enrichment for previously annotated gene-gene relationships (Boyle et al., 2018; Kim et al., 2019). As a side note, nearest neighbor graphs are also the input to popular manifold learning algorithms t-SNE and UMAP, which tend to capture local structure in biological data. We use nearest neighbor gene similarity and cell context similarity graphs as the basis for the graph regularization objectives described above, using cosine similarity and five nearest neighbors for both graphs (unless otherwise specified below).
Our second customization involves the dictionary learning initialization step. As DGRDL is an iterative optimization algorithm, it requires a pre-initialized dictionary in order to perform its first iteration. In the absence of a pre-initialized dictionary, DGRDL chooses k random elements among the input training signals to serve as the initial dictionary. We found empirically that this random selection introduced variability in the optimization outcomes. As a result, we pass a pre-initialized dictionary to DGRDL in the form of k representative training signals chosen via k-medoids from among the input training signals, using the MATLAB kmedoids function. As k-medoids is a clustering algorithm, the initial dictionary can be thought of as optimal for clustering the data into k mutually exclusive groups. From this starting point, an new dictionary is learned that best approximates all m training signals in terms of t dictionary elements while preserving local structure of the data. As t >1, this process can be thought of as relaxing the one-hot clustering assumptions present in the initial dictionary. Compared to random initialization, we found that this reduced the root mean squared error of our factorizations by 9% on the DepMap dataset.
Finally, we multiply the sparse representation matrix X with a scalar correction factor 1/sqrt(n) to convert coefficients into units of standard deviation from their original unit of Euclidean distance. As these coefficients are analogous to the loading coefficients used in PCA, we refer to this matrix of coefficients as the loadings matrix in the manuscript.
This concludes the descriptions of the core algorithmic steps performed with Webster in the manuscript. The following sections describe experimental methods. The “Quantification and statistical analysis” section describes the application of Webster to various datasets, as well as the annotation and visualization steps performed on the resulting Webster output.
C7orf26 cloning
Two C7orf26 transcript isoforms were used in this study. The full length isoform (C7orf26_v1), corresponds to the Ensembl transcript ENST00000344417 (Origene, RC219786L4). The second isoform (C7orf26_v2), corresponds to the Ensembl transcript ENST00000359073 and was acquired through Broad Genetic Perturbation Platform (TRCN0000477172). Both coding sequences were subcloned from their respective sources into the pDONR221 vector using PCR amplification and Gateway BP cloning, and subsequently shuttled into pLX307 and pLX_HA expression vectors using Gateway LR reactions. The pLX307 expresses the protein under an EF1alpha promoter with a C-terminal V5 tag. The pLX_HA vector, which we created for this study, is a modified version of pLX307 carrying the HA tag instead of the V5 tag.
C7orf26_V1 sequence (no stop codon)
ATGAGCGACATCCGCCACTCGCTGCTGCGCCGCGATGCGCTGAGCGCCGCCAAGGAGGTGTTGTACCACCTGGACATCTACTT CAGCAGCCAGCTGCAGAGCGCGCCGCTGCCCATCGTGGACAAGGGCCCCGTGGAGCTGCTGGAGGAGTTCGTGTTCCAGGTG CCCAAGGAGCGCAGCGCGCAGCCCAAGAGACTGAATTCCCTTCAGGAGCTTCAACTTCTTGAAATCATGTGCAATTATTTCCAGG AGCAAACCAAGGACTCTGTTCGGCAGATTATTTTTTCATCCCTTTTCAGCCCTCAAGGGAACAAAGCCGATGACAGCCGGATGAG CTTGTTGGGAAAACTGGTCTCCATGGCGGTGGCTGTGTGTCGAATCCCGGTGTTGGAGTGTGCTGCCTCCTGGCTTCAGCGGAC GCCCGTGGTTTACTGTGTGAGGTTAGCCAAGGCCCTTGTAGATGACTACTGCTGTTTGGTGCCGGGATCCATTCAGACGCTGAAG CAGATATTCAGTGCCAGCCCGAGATTCTGCTGCCAGTTCATCACCTCCGTTACCGCGCTCTATGACCTGTCATCAGATGACCTCA TTCCACCTATGGACTTGCTTGAAATGATTGTCACCTGGATTTTTGAGGACCCAAGGTTGATTCTCATCACTTTTTTAAATACTCCGAT TGCGGCCAATCTGCCAATAGGATTCTTAGAGCTCACCCCGCTCGTTGGATTGATCCGCTGGTGCGTGAAGGCACCCCTGGCTTAT AAAAGGAAAAAGAAGCCCCCCTTATCCAATGGCCATGTCAGCAACAAGGTCACAAAGGACCCGGGCGTGGGGATGGACAGAGA CTCCCACCTCTTGTACTCAAAACTCCACCTCAGCGTCCTGCAAGTGCTCATGACGCTGCAGCTGCACCTGACCGAGAAGAATCTG TATGGGCGCCTGGGGCTGATCCTCTTCGACCACATGGTCCCGCTGGTAGAGGAGATCAACAGGTTGGCGGATGAACTGAACCCC CTCAACGCCTCCCAGGAGATTGAGCTCTCGCTGGACCGGCTGGCGCAGGCTCTGCAGGTGGCCATGGCCTCAGGAGCTCTGCT GTGCACGAGAGATGACCTGAGAACCTTGTGCTCCAGGCTGCCCCATAATAACCTCCTCCAGCTGGTGATCTCGGGTCCCGTGCA GCAGTCGCCTCACGCCGCGCTCCCCCCGGGGTTCTACCCCCACATCCACACGCCCCCGCTGGGCTACGGGGCTGTCCCGGCC CACCCCGCCGCCCACCCCGCCCTGCCCACGCACCCCGGCCACACCTTCATCTCCGGCGTGACCTTTCCCTTCAGGC
C7orf26_V2 sequence (no stop codon)
ATGAGCGACATCCGCCACTCGCTGCTGCGCCGCGATGCGCTGAGCGCCGCCAAGGAGGTGTTGTACCACCTGGACATCTACTT CAGCAGCCAGCTGCAGAGCGCGCCGCTGCCCATCGTGGACAAGGGCCCCGTGGAGCTGCTGGAGGAGTTCGTGTTCCAGGTG CCCAAGGAGCGCAGCGCGCAGCCCAAGGAGCAAACCAAGGACTCTGTTCGGCAGATTATTTTTTCATCCCTTTTCAGCCCTCAAG GGAACAAAGCCGATGACAGCCGGATGAGCTTGTTGGGAAAACTGGTCTCCATGGCGGTGGCTGTGTGTCGAATCCCGGTGTTGG AGTGTGCTGCCTCCTGGCTTCAGCGGACGCCCGTGGTTTACTGTGTGAGGTTAGCCAAGGCCCTTGTAGATGACTACTGCTGTTT GGTGCCGGGATCCATTCAGACGCTGAAGCAGATATTCAGTGCCAGCCCGAGATTCTGCTGCCAGTTCATCACCTCCGTTACCGC GCTCTATGACCTGTCATCAGATGACCTCATTCCACCTATGGACTTGCTTGAAATGATTGTCACCTGGATTTTTGAGGACCCAAGCG TCCTGCAAGTGCTCATGACGCTGCAGCTGCACCTGACCGAGAAGAATCTGTATGGGCGCCTGGGGCTGATCCTCTTCGACCACA TGGTCCCGCTGGTAGAGGAGATCAACAGGTTGGCGGATGAACTGAACCCCCTCAACGCCTCCCAGGAGATTGAGCTCTCGCTGG ACCGGCTGGCGCAGGCTCTGCAGGTGGCCATGGCCTCAGGAGCTCTGCTGTGCACGAGAGATGACCTGAGAACCTTGTGCTCC AGGCTGCCCCATAATAACCTCCTCCAGCTGGTGATCTCGGGTCCCGTGCAGCAGTCGCCTCACGCCGCGCTCCCCCCGGGGTT CTACCCCCACATCCACACGCCCCCGCTGGGCTACGGGGCTGTCCCGGCCCACCCCGCCGCCCACCCCGCCCTGCCCACGCA CCCCGGCCACACCTTCATCTCCGGCGTGACCTTTCCCTTCAGGCCCATCCGC
CRISPR guide cloning
Each guide RNA (gRNA) for CRISPR-Cas9 mediated gene knockout was selected from the Avana CRISPR-Cas9 guide library (Sanson et al., 2018). Guides were ranked by their guide efficacy score inferred by CERES during its processing of Cancer Dependency Map data (Meyers et al., 2017), available through the Dependency Map Portal (Achilles_guide_efficacy.csv, https://depmap.org/portal/download/). Oligonucleotides containing the gRNA sequence were cloned via Golden Gate Assembly into the lentiCRISPR_v2_Blast plasmid backbone, which is identical to the lentiCRISPR_v2 (https://www.addgene.org/52961/) but with the puromycin selection cassette swapped out for a blasticidin selection cassette. The gRNA sequences are described in the key resources table.
Lentivirus production and infection
To produce lentivirus, expression vectors (of proteins or guides) were co-transfected with psPAX2 and pMD2.G second generation virus packaging vectors into 293T cells using Mirus LT-1 Transfection Reagent (Mirus) according to the manufacturer’s recommendations. Cells were spin infected with viral supernatant mixed with final concentration of 4 ug/mL polybrene (Sigma Aldrich) and centrifuged at 2200 RPM for 1 hour. After 24 hours of viral infection, media was exchanged with fresh media containing either 10 ug / mL of puromycin (for the pLX series of vectors) or 20 ug / mL of blasticidin S HCl (for the pLenti_V2_Blast series of vectors). Selection media was maintained for the duration of use of the infected cells.
Whole cell lysates
For harvesting total protein lysate, cells were washed twice with ice cold PBS buffer and lysed using RIPA buffer (R0278; Sigma-Aldrich) containing Halt Protease Inhibitor Cocktail (Thermo Fisher) and 1:100 of 1mM Phenylmethylsulfonyl fluoride (PMSF) (Gold-bio, P-470–25), rotated for 30 minutes in the cold room, spun down at max speed on a tabletop ultracentrifuge for 10 minutes, and the pellet (containing genomic DNA) removed. The resulting lysate was quantified using BCA Protein Assay Kit (Thermo Fisher; 23227).
Nuclear lysates
For harvesting nuclear protein lysate, we performed our protocol from (Mashtalir et al., 2018). Cells were washed twice with ice cold PBS buffer and resuspended in EB0 hypotonic buffer (50mM Tris pH 7.5, 0.1% NP-40, 1mM EDTA, 1mM MgCl2) containing 1:100 of Halt Protease Inhibitor Cocktail and 1:100 of 1mM PMSF. Lysate was spun down at 5,000rpm for 5min at 4C, and the supernatant containing cytoplasmic extract was discarded. Pelleted nuclei were resuspended in EB300 high salt buffer (50mM Tris pH 7.5, 300mM NaCl, 1% NP-40, 1mM EDTA, 1mM MgCl2) containing 1:100 of Halt Protease Inhibitor Cocktail and 10 μM PMSF. Lysates were incubated on ice for 10 min with occasional vortexing. Lysate was spun down at 21000 g for 10 min at 4C. The pellet containing genomic DNA was discarded. Supernatants consisting of nuclear lysate were quantified using BCA.
Immunoprecipitation and mass spectrometry of exogenously expressed protein
293T cells overexpressing either C7orf26_V1 or C7orf26_V2 were prepared using lentivirus and selected using puromycin as described above. Parental cell lines with no overexpression construct were passaged in parallel for the ‘Mock’ control. For large scale purifications, 5 plates of confluent 15 cm plates were harvested and subjected to the nuclear lysate protocol described above. The resulting lysates for each condition were diluted to 1 mg / mL in EB300.
For HA purifications, 5 mL of nuclear lysate from each condition was incubated with 250 uL of Pierce HA Magnetic Beads (Thermo Fisher, 88836) and rotated overnight at 4C. Afterwards, beads were collected using a magnetic rack and washed 6× with EB300 and 2× with PBS buffer all at 4C. We eluted precipitated protein from the beads using low pH elution in glycine buffer as described (https://www.abcam.com/protocols/immunoprecipitation-protocol-1#elution). For V5 purifications, the same protocol was performed but with Anti-V5 Agarose Affinity Gel (Sigma-Aldrich, A7345–1ML). A portion of samples were saved for immunoblot analysis, and the remainder was to mass spectrometry with the Taplin Mass Spectrometry Facility, the full details of which are previously described under “Sample Preparation” (Mashtalir et al., 2018). The resulting total peptide counts for each protein were reported.
CRISPR-Cas9 mediated gene knockout of INTS6, INTS10, and C7orf26
Cells harboring knockout of INTS6, INTS10 and C7orf26 were generated using the above lentiviral infection protocol. After one week of selection under blasticidin, cells were harvested using the whole cell lysate protocol described above. For the INTS10 clonal knockout lines used for the endogenous immunoprecipitation experiment, cells were plated at single cell dilution and grown for 3 weeks with media changes. Single cell colonies were picked and whole cell lysate protocol was repeated to identify clonal lines harboring complete INTS10 knockout. Successful clones were subjected to nuclear lysis in preparation for endogenous immunoprecipitation.
Endogenous protein immunoprecipitation
From quantified nuclear lysates, we diluted all lysates with EB300 buffer to a concentration of 1 mg/mL. We used 100 ug of nuclear lysate for each immunoprecipitation condition. We added 1.25 μg of antibody to each condition. An antibody raised against C7orf26 (Novus, NBP2–14764) was used, and a mouse IgG antibody (Santa Cruz, No. sc-2025) was used as a negative control. After rotation overnight at 4C, Protein G Dynabeads (Thermo Fisher, 10004D) were added and rotated for 2 hours. Using a magnetic rack, beads were isolated from the lysate, washed 6× in EB300 buffer and 2× in PBS buffer. The resulting immunoprecipitated protein was eluted from the beads using LDS buffer.
Density sedimentation gradientgradient
Density gradient sedimentation was performed as previously described (Mashtalir et al., 2018). 750 ug of nuclear extract from 293T cells was overlaid on onto an 11 ml 10–30% glycerol gradient, prepared in a 14 × 89 mm polyallomer centrifuge tube. Tubes were centrifuged in an SW40 rotor at 4 °C for 16 h at 40,000 r.p.m. 550 ml fractions were collected by hand. Fractions were concentrated by adding a 1:10 volume/volume ratio of Strataclean beads to the collected fractions, incubated under rotation in the cold room, and eluted using LDS buffer. A total of 23 fractions were collected. Fractions 1–15, representing the lower molecular weights, were loaded and used in immunoblot analyses.
Immunoblot analysis
All samples were loaded and run on a pre-poured 4%–12% Bis-Tris gel (Thermo Fisher, NP0323) in MES buffer (Thermo Fisher, NP0002), and transferred onto nitrocellulose membrane (Thermo Fisher, IB23001) utilizing iBlot 2 Dry Blotting System (Thermo Fisher, IB21001). After 1 hr blocking incubation in 5% milk solution and subsequent washes, all immunoblots were incubated with indicated primary antibodies for overnight at 4C or at room temperature for 3 hours. Blots were then incubated with indicated secondary antibody for 1 hour at room temperature, and immunoblots were imaged using Odyssey CLx infrared imager (LICOR).
For input samples, 20 ug of protein was loaded. For immunoprecipitated samples, a fractional volume of the total eluate was run for immunoblotting. For density sedimentation gradient fractions, a fractional volume of the total eluate from Strataclean beads was loaded for each fraction. For the ladder, 5 uL of Pageruler Plus (Thermo Fisher, 26619) was added. The antibodies used for blotting are described in the key resources table.
QUANTIFICATION AND STATISTICAL ANALYSIS
Fitness data origins and preprocessing
The genotoxic screening collection was downloaded from the publisher’s website (see their Table S2. CRISPR Screens NormZ results) (Olivieri et al., 2020). The dataset consisted of 17,382 measured gene effects over 31 fitness screens performed in the presence of low doses of genotoxins. Each of the 31 screens was already processed through normZ which centers and scales the data (Colic et al., 2019).
To select high-variance genes, we assumed that a large portion of gene effects in genome-scale screens have no phenotype in any cell contexts (also known as non-essential genes). Any variance present in these gene effects will be due to experimental noise rather than biological signal. The distribution of these across-cell-line variances will follow a chi-squared distribution, which converges to a normal distribution with large n. Biologically driven gene effects will exhibit greater variation across cell lines and will form positive outliers in this normal distribution. To detect such outliers, we used a quantile-quantile plot to visualize the observed distribution of gene effect variances compared to a theoretical normal distribution. We drew a cutoff that separated high variance genes from the remaining (variance > 3), resulting in 304 gene effects over 31 screens that formed the input to graph regularized dictionary learning.
The 19Q4 Broad Cancer Dependency Map screening collection was downloaded from the Cancer Dependency Map FigShare archive (under the file Achilles_gene_effect.csv, https://doi.org/10.6084/m9.figshare.11384241.v3). The raw dataset consisted of 18,333 gene effect measurements over 689 cancer cell lines. We filtered out a group of cell lines that suffered a batch effect due to PCR contamination. We filtered out a group of X-chromosomal genes whose copy number across cell lines could not be properly controlled for. We also filtered out two HUGO gene groups, olfactory genes (https://www.genenames.org/data/genegroup/#!/group/141) and KRTAP genes (https://www.genenames.org/data/genegroup/#!/group/619), whose high sequence similarity resulted in large-scale off target guide cutting activity as previously described (Boyle et al., 2018). This intermediate dataset consisted of 17,167 gene effect measurements over 675 cell lines.
We applied several correction measures before gene effect selection. The first was a generalized correction for cutting effects specific to chromosome arms, as reported previously (Amici et al., 2021). We then centered each cell line screen and applied a batch correction for screen quality. This was done by linearly regressing out the NNMD profile over cell lines from each gene effect profile. NNMD stands for null-normalized mean difference and was previously described (Dempster et al., 2019). The NNMD score for each cell line was obtained from the “NNMD” column the sample_info.csv file from Figshare archive (https://doi.org/10.6084/m9.figshare.11384241.v3). After screen quality correction, we scaled each cell line screen. This dataset was used as input for gene effect selection.
For gene effect selection, we used three criteria:
Variance
Perturbation confidence
Maximum pairwise correlation with other gene effects
The cutoff for variance was chosen using a quantile-quantile plot, as with the genotoxic screening data above. A variance cutoff of 1 was used. The perturbation confidence score was calculated as described previously (http://archive.today/2021.03.22–122633/https://cancerdatascience.org/blog/posts/gene_confidence_blog/). In brief, an XGBoost model was trained to discriminate between known low confidence gene perturbations and high confidence gene perturbations using various features derived from the individual guide RNA effects. The recommended cutoff of 0.5 was applied. From these gene effects, we kept those that exhibited a maximum pairwise correlation with other gene effects above a certain threshold, as done in yeast fitness screen analyses (Costanzo et al., 2010, 2016). The threshold we used was 0.275. This resulted in a preprocessed matrix of 2,921 gene effect measurements over 675 cell lines that formed the input to graph regularized dictionary learning.
Sanger Institute screens processed through the CERES algorithm were downloaded from the Cancer Dependency Map FigShare archive (under the filename sample_info.csv, https://doi.org/10.6084/m9.figshare.9116732.v2). The raw data consisted of 17,716 gene effect measurements over 318 cell lines. Arm correction, centering, NNMD regression and scaling were applied.
Hyperparameter tuning and model selection
For the genotoxic fitness screens, we empirically chose the primary dictionary learning hyperparameter k (dictionary size) by sweeping between values of 1 and 31 while fixing t = 2. We evaluated each of the model objectives and looked for diminishing returns for the approximation error and gene Laplacian model objectives (the cell context Laplacian had a linear relationship with k, so it was less informative for model selection). Diminishing returns were reached at k = 10. For a comparison, we also swept across k while fixing t = 1 (representing hard clustering). We also repeated these experiments without graph regularization (by setting α and β to 0).
For the cancer cell fitness screens, we performed a grid search over k = 25 to 675 in steps of 25, and t = 1:8, resulting in 216 model instances. From this search, we selected t = 4, as this was the sparsest model parameter whose objectives remained well behaved for all values of k. Subsequently, we performed a second sweep over k = 25 to 675 in steps of 5, with t fixed at 4, resulting in 131 model instances. Diminishing returns in the approximation error and gene Laplacian model objectives were observed at k = 220, which we chose for the final factorization. We confirmed that model objectives for these hyperparameter choices were stable to random seed initialization.
Various other model hyperparameters were set to the default values recommended in the original paper (Yankelevsky and Elad, 2016), and were as follows: α = 0.2; β = 0.6; number of iterations = 20. Finally, we set the graph regularization terms according to the settings explained above: neighbor graph degree = 5; neighbor graph metric/edgeweight = cosine similarity.
Dictionary learning experiments: Robustness, denoising, and transferability
To assess robustness, we performed DGRDL with different random seed initializations, using the same k-medoids initialized dictionary. Element-wide consistency between the resulting dictionaries was assessed using Pearson correlation.
To assess the denoising properties of dictionary learning on fitness data, we created four noisy versions of the cancer cell fitness screening dataset by adding Gaussian random noise. The Gaussian random noise matrices were created using the R function rnorm with standard deviations set to a variety of values (SD = 0.25, 0.5, 1, 1.5). We also randomly split the 2,921 gene effects in cancer cells into 2,191 training genes and 730 test genes.
For each of the five datasets (original data and four noise levels), we trained DGRDL on the training gene effects only (using k = 220, t = 4) and subsequently modeled the corresponding unseen test genes in terms of dictionary elements (with the same noise level present in the test and training genes). Each reconstructed test gene was subsequently compared to the corresponding gene effect in the raw data (which did not have additional synthetic noise added) using Pearson correlation as a metric. We repeated this entire process five times, and kept the mean Pearson correlation for each test gene at each noise level. For each noise level, the distribution of these resulting scores were plotted as a distribution.
For the transferability experiments, we used a dictionary trained on data measured by one institute (Broad) to model the corresponding gene effects measured by another institute (Sanger), which used different experimental conditions and CRISR-Cas9 guide RNA sequences for each gene. We took a dictionary trained on the full Broad 2,191 gene effects over 675 cell lines (k = 220, t = 4) and subsetted it to the 161 cell lines that were screened by both institutes. For the Broad and Sanger datasets, we modeled the corresponding 2,901 overlapping gene effects across the 161 common cell lines in terms of the same Broad-trained dictionary. The resulting approximations were assessed using Pearson correlation and were plotted as a distribution for each dataset. As a comparison, a dictionary with shuffled cell line annotations was used to model the 2,901 Sanger-measured gene effects.
Neighbor graph embedding to visualize gene function landscapes
For visualizing genotoxic and cancer cell fitness screen collections, we utilized the UMAP approach (McInnes et al., 2018) as implemented by the R umap package. In each case, two matrices were concatenated and used as input: the preprocessed gene effects that served as inputs to Webster, and the dictionary matrix that is outputted by Webster. For the genotoxic screens, the 304 gene effects and 10 functional effects were plotted using the following UMAP parameters: metric = “pearson”, num_neighbors = 15. For the cancer cell fitness screens, the 2,921 gene effects and 220 functional effects were plotted using the following UMAP parameters: metric = “pearson”, num_neighbors = 10. All other parameters were set to default.
Annotation of learned functions
Dictionary elements learned by Webster from each screen collection were annotated as follows. For each of the ten dictionary elements learned from genotoxic fitness screens, we considered, in order of priority, (1) strongly loaded genes and (2) which treatments induced a strong fitness effect. For the first of the five dictionary elements, the strongly loaded genes on each mapped to one of five classical DNA damage response pathways. These relationships were corroborated by the set of treatments that induce fitness effects in these genes. For three of the dictionary elements, only a single treatment induced a strong fitness effect on its loaded genes. These were representative of the resistance / sensitivity profiles of these specific treatments, which we corroborated by matching its strongly loaded genes against similar screens from the literature. Finally, two dictionary elements exhibited strong enrichment for common essential genes and proliferation suppressor genes in their highly loaded genes, annotations for which were taken from the literature (Colic et al., 2019; Hart et al., 2015).
For each of the 220 dictionary elements learned from the cancer cell fitness screens, we again considered, in order of importance, (1) strongly loaded genes and (2) top genomic features from models trained to predict the function’s fitness profile over cell lines (see below). For annotations of the strongly loaded genes, we used a gene annotation web service, gProfiler, that takes a ranked list of genes as input and outputs a ranked list of enriched genesets (Raudvere et al., 2019). We supplemented these annotations with corresponding ones from STRING (Szklarczyk et al., 2015). We searched the literature for additional insights and recently published corroborating papers when applicable. Finally, we performed biomarker association analysis using cell line features, described below.
Using a combination of geneset enrichments, specific literature annotations for the top loaded genes and cell line features, we were able to manually annotate each dictionary element. Of the 220 dictionary elements, 199 elements were mapped to a biological function using manual curation by the authors. Of these, 195 were annotated according to geneset enrichments among top loaded genes, and 4 were named based on a clear biomarker. Nineteen of the dictionary elements were highly loaded for essential genes, which incur fitness effects at the lower detection limit of our assay and group together in our analysis for that reason. These functions were labeled as “Common Essential (Gene)”, where the Gene was chosen to be the top loaded gene, or “Common Essential (Chr#)”, when the common essential genes shared synteny on chromosome regions (Amici et al., 2021). Finally, two dictionary elements could not be mapped to a biological process. On deeper examination, the top loaded genes for both of these functions were perturbed using Avana CRISPR-Cas9 guides that targeted non-unique genomic sequences, suggesting that these elements represented technical factors that were separated from the remainder of the data. We labeled these as “[Gene] (unclear)”.
Associating fitness effects with baseline genomic features of cell lines
Baseline genomic features were associated to each function using predictive modeling. Using the function’s inferred fitness effect across cell lines as the target, we performed random forest regression using the following features from the DepMap 21Q2 release (https://doi.org/10.6084/m9.figshare.14541774.v2):
RNAseq expression
copy number
boolean mutation matrices
Methylation
Proteomics
Lineage
metabolomics data
The numerical features were normalized and the categorical features were one-hot encoded and then combined into a feature matrix. These features were then used to predict the target fitness profile using 5-fold cross validation, using Pearson correlation as the metric for model performance. We selected the top 1000 features in each fold using the f-regression metric to fit the model to the target. A final model was trained on all the data and the feature importances were extracted from that model to help determine the likely features that were most important in these predictions. In certain cases, cell lines strongly dependent on a certain function harbored interpretable predictive features; those are reported in the paper when applicable, and were used to corroborate the function name chosen as described above.
Plotting pleiotropic networks
For the Cancer Dependency Map dataset, we estimated the fraction of fitness genes that were pleiotropic. For the denominator, we used the number of genes whose approximation by Webster had a Pearson score of 0.4 or higher compared to its original measured gene effect (2498 genes). We then reported the fraction of these genes whose loadings onto two or more functions meets or exceeds 0.25 SD (1320 genes).
For network visualizations of pleiotropy, we start with a set of functions. Each pair of functions is connected by an edge if they share at least one pleiotropic gene (defined by the criteria above) which is loaded onto both functions. The width of this edge is proportional to the number of pleiotropic genes they share. Networks were visualized using the R graph package.
Protein complex annotations
Curated annotations for modular protein complexes were taken from the literature. Sources were used that identified modules using either structural or other biochemical means (biochemical purification of intact complexes compared to knockout of key subunits). The sources were as follows:
STAGA/ATAC complexes (Spedale et al., 2012)
SWI/SNF complexes (Mashtalir et al., 2018).
Mediator complex (Tsai et al., 2014).
Integrator complex (Pfleiderer and Galej, 2021; Sabath et al., 2020; Tilley et al., 2021; Zheng et al., 2020)
Subcellular localization analyses
The Human Cell Map project profiled bait-prey interactions in human cells using proximity ligation. We downloaded their subcellular localization inferences for 4,424 proteins across 20 subcellular locations (Go et al., 2021). Of these proteins, 1,463 had corresponding gene effects as part of the Webster analysis in cancer cell fitness screen, so their data was filtered to a dense matrix of 1,463 protein localization profiles, and the Webster loadings matrix was filtered to the same set of 1,463 genes assigned loaded across 220 inferred biological functions.
To ask whether highly loaded genes in specific functions shared subcellular localization annotations, we took the matrix product, which resulted in a new matrix of 220 functions scored across 20 localizations. Each of the 220 rows of this matrix is the sum of the individual protein-level localization distributions weighted by their loading score on that function. This was used for the basis of subcellular localization analysis of our Webster inferred functions.
We noted during clustering of the 20 subcellular localizations (both in the original NMF matrix as well as this new matrix product) that each could be grouped into one of seven interpretable compartments. These compartment level annotations were used throughout the paper.
Finally, we report the localization specificity of individual functions. For each of the 220 functions, the entropy of its distribution over 20 localizations was calculated using the R entropy package, and the resulting 220 entropy scores were rescaled such that lowest entropy distributions were assigned a new “Specificity” score of 1, while the highest entropy distributions were assigned a score of 0.
Compound sensitivity data
PRISM Primary Screen compound sensitivity data was obtained from the Drug Repurposing Hub Figshare archive (primary-screen-replicate-collapsed-logfold-change.csv, https://doi.org/10.6084/m9.figshare.9393293.v4). The raw data matrix consisted of 5,274 compound sensitivity profiles measured over 578 cell lines using a 2.5 uM dose treatment. To eliminate cell line quality effects, we subtracted a trimmed mean of each cell line profile from each compound sensitivity profile.
To prepare the data for modeling in terms of Webster’s latent functions, we selected compound classes representing known mechanisms of action, for which there were at least 5 compound sensitivity profiles in the primary screen. This matrix contained missing values, which were imputed using the R package FastImputation. Finally, we kept those cell lines that were also screened in the CRISPR-Cas9 fitness dataset.
The final compound sensitivity profiles with known MOA’s consisted of 191 compound sensitivity profiles over 367 cell lines. Each compound was modeled in terms of the dictionary matrix learned from CRISPR-Cas9 gene perturbation, filtered to the same 367 cell lines. The modeling was performed with orthogonal matching pursuit with t = 4, such that each compound sensitivity profile was modeled as a sparse combination of four dictionary elements.
The 191 compound sensitivity profiles were added as data points to the UMAP gene function plot by reconstructing each compound sensitivity profile using full-sized dictionary elements (675 cell lines), and using the R predict function to add the imputed profile to the previously learned R umap object.
These steps were repeated for the PRISM Secondary Screen compound sensitivity data, in which the same compounds as above were treated at multiple dose points.
Synthetic data example
The synthetic dictionary in R25×2 was generated as follows. Selectively essential biological functions exhibit skewed distributions in their fitness effects across cell contexts. Accordingly, we simulated the fitness effects of two biological functions over 25 cell contexts by generating two random vectors with skew normal distributions, using the dsn function in R (parameters: xi = 0.1, omega = 0.3, alpha = 5). Empirically, such fitness effects are rarely perfectly orthogonal, as cancer cell lines can exhibit more than one rate limiting dependency for growth. Therefore we generated the above vectors to have a slight correlation to one another (cosine similarity = 0.2).
The loadings matrix in R2×100 was constructed by concatenating the following repeated columns: [2,0] 40 times, [0,2] 40 times, [1,1] 20 times. This corresponds to 40 genes mapping to Function 1, 40 genes mapping to Function 2, and 20 genes mapping equally to both.
The synthetic fitness measurements were generated by taking the matrix product of the synthetic dictionary in R25×2 and the loadings matrix in R2×100 resulting in a noiseless gene effect matrix in R25×100, to which normally distributed random noise was added (generated by the rnorm function in R using 0.3 standard deviation).
From this input, various factorizations were performed. PCA was run with the prcomp function in R and the first two components were kept. ICA was run using the clusterFastICARuns function in the MineICA R package, which is based off the MATLAB icasso function (http://research.ics.aalto.fi/ica/icasso/), which aggregates repeated runs of FastICA (https://research.ics.aalto.fi/ica/fastica/) to report more stable components. ICA was set to find two components. K-means was run using the kmeans function in R, with k = 2. Webster was run with k = 2, t = 2, with neighbor graph degree = 1.
Additional factorization of genotoxic screening data
For PCA applied to the genotoxic screening dataset, we set the number of components to 8, which was automatically chosen according to an “elbow plot” of the eigenvalues corresponding to each component in the model, using the quickelbow function in the R package bigpca. For ICA, we set the number of components to 13, according to the MSTD score from (Kairov et al., 2017), which calculates an optimal number of stable ICA components.
To compare the Webster, PCA and ICA factorizations, we computed an individual AUROC for each geneset defined by (Olivieri et al., 2020) for each inferred component, using the roc_auc function in the R package yardstick. This computes the enrichment specificity of each geneset across components, according to the rank order of genes by their loading scores on that component.
Supplementary Material
Highlights.
Webster infers gene multifunctionality from high-dimensional gene perturbation data
A matrix of gene effects is compressed into a low-rank dictionary of functional effects
Each gene effect is sparsely modeled as a pleiotropic mixture of functional effects
Projecting compound sensitivity profiles into this latent space recovers drug MOA
ACKNOWLEDGMENTS
Work was funded by U01 CA176058 (W.C.H.) and NIH/NCI F32CA243290 (J.J.K.). M.Z. is supported, in part, by NSF under nos. IIS2030459 and IIS2033384, the Harvard Data Science Initiative, the Amazon Research Award, and the Bayer Early Excellence in Science Award. We thank members of the Hahn lab and the Cancer Data Science team, as well as Caleb Laureau, Peter Winter, Kevin Zhan, Luc de Waal, Edmond Chan, Mustafa Kocak, Ed Huttlin, and Niklas Rindorff for helpful feedback and discussions. Thank you to Yael Yankelevsky for answering many questions about graph-regularized dictionary learning. Thank you to Ben Cooley, Andrew Tang, Nena Berg, and Kat Huang of the Pattern Team @ Broad (https://pattern.broadinstitute.org/) for developing the minisite. Thank you to Mariya Kazachkova for sharing her arm correction script. We thank the Taplin Mass Spectrometry Facility’s Ross Tomaino for processing and analysis of the mass spectrometry samples (https://taplin.med.harvard.edu/home). The following figures were created with BioRender.com: Figures 1A, 1B, 2A, 3A, 4A–4C, 5A, and 5E. Chemical compound 3D structures are from PubChem.
DECLARATION OF INTERESTS
F.V. receives research support from Novo Ventures. A.T. is a consultant for Cedilla Therapeutics, Foghorn Therapeutics, and The Center for Protein Degradation (Deerfield) and is an SAB member and holds equity in Turbine Simulated Cell Technologies. W.C.H. is a consultant for Thermo Fisher, Solasta Ventures, MPM Capital, KSQ Therapeutics, iTeos, Tyra Biosciences, Jubilant Therapeutics, RAPPTA Therapeutics, Frontier Medicine, Calyx, and Function Oncology.
Footnotes
INCLUSION AND DIVERSITY
We worked to ensure diversity in experimental samples through the selection of the cell lines. We worked to ensure diversity in experimental samples through the selection of the genomic datasets. One or more of the authors of this paper self-identifies as an underrepresented ethnic minority in science. The author list of this paper includes contributors from the location where the research was conducted who participated in the data collection, design, analysis, and/or interpretation of the work.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.cels.2021.12.005.
ADDITIONAL RESOURCES
An interactive portal to explore Webster’s output can be found at https://depmap.org/webster/.
REFERENCES
- Ameziane N, May P, Haitjema A, van de Vrugt HJ, van Rossum-Fikkert SE, Ristic D, Williams GJ, Balk J, Rockx D, Li H, et al. (2015). A novel Fanconi anaemia subtype associated with a dominant-negative mutation in RAD51. Nat. Commun. 6, 8829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amici DR, Jackson JM, Truica MI, Smith RS, Abdulkadir SA, and Mendillo ML (2021). FIREWORKS: A bottom-up approach to integrative co-essentiality network analysis. Life Sci. Alliance 4, e202000882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aregger M, Lawson KA, Billmann M, Costanzo M, Tong AHY, Chan K, Rahman M, Brown KR, Ross C, Usaj M, et al. (2020). Systematic mapping of genetic interactions for de novo fatty acid synthesis identifies C12orf49 as a regulator of lipid metabolism. Nat. Metab. 2, 499–513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baillat D, Russell WK, and Wagner EJ (2016). CRISPR-Cas9 mediated genetic engineering for the purification of the endogenous integrator complex from mammalian cells. Protein Expr. Purif. 128, 101–108. [DOI] [PubMed] [Google Scholar]
- Baillat D, and Wagner EJ (2015). Integrator: Surprisingly diverse functions in gene expression. Trends Biochem. Sci. 40, 257–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbieri E, Trizzino M, Welsh SA, Owens TA, Calabretta B, Carroll M, Sarma K, and Gardini A (2018). Targeted enhancer activation by a subunit of the integrator complex. Mol. Cell 71, 103–116.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barghout SH, Aman A, Nouri K, Blatman Z, Arevalo K, Thomas GE, MacLean N, Hurren R, Ketela T, Saini M, et al. (2021). A genome-wide CRISPR/Cas9 screen in acute myeloid leukemia cells identifies regulators of TAK-243 sensitivity. JCI Insight 6, e141518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barish S, Barakat TS, Michel BC, Mashtalir N, Phillips JB, Valencia AM, Ugur B, Wegner J, Scott TM, Bostwick B, et al. (2020). BICRA, a SWI/SNF complex member, is associated with BAF-disorder related phenotypes in humans and model organisms. Am. J. Hum. Genet. 107, 1096–1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayraktar EC, La K, Karpman K, Unlu G, Ozerdem C, Ritter DJ, Alwaseem H, Molina H, Hoffmann HH, Millner A, et al. (2020). Metabolic coessentiality mapping identifies C12orf49 as a regulator of SREBP processing and cholesterol metabolism. Nat. Metab. 2, 487–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behan FM, Iorio F, Picco G, Gonçalves E, Beaver CM, Migliardi G, Santos R, Rao Y, Sassi F, Pinnelli M, et al. (2019). Prioritization of cancer therapeutic targets using CRISPR-Cas9 screens. Nature 568, 511–516. [DOI] [PubMed] [Google Scholar]
- Boeing S, Williamson L, Encheva V, Gori I, Saunders RE, Instrell R, Aygün O, Rodriguez-Martinez M, Weems JC, Kelly GP, et al. (2016). Multiomic analysis of the UV-induced DNA damage response. Cell Rep 15, 1597–1610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boleda G (2020). Distributional semantics and linguistic theory. Annu. Rev. Linguist. 6, 213–234. [Google Scholar]
- Boyle EA, Pritchard JK, and Greenleaf WJ (2018). High-resolution mapping of cancer cell networks using co-functional interactions. Mol. Syst. Biol. 14, e8594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleary B, Cong L, Cheung A, Lander ES, and Regev A (2017). Efficient generation of transcriptomic profiles by random composite measurements. Cell 171, 1424–1436.e18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colic M, Wang G, Zimmermann M, Mascall K, McLaughlin M, Bertolet L, Lenoir WF, Moffat J, Angers S, Durocher D, et al. (2019). Identifying chemogenetic interactions from CRISPR screens with drugZ. Genome Med 11, 52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corsello SM, Nagari RT, Spangler RD, Rossen J, Kocak M, Bryan JG, Humeidi R, Peck D, Wu X, Tang AA, et al. (2020). Discovering the anti-cancer potential of non-oncology drugs by systematic viability profiling. Nat. Cancer 1, 235–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costanzo M, Baryshnikova A, Bellay J, Kim Y, Spear ED, Sevier CS, Ding H, Koh JLY, Toufighi K, Mostafavi S, et al. (2010). The genetic landscape of a cell. Science 327, 425–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costanzo M, Kuzmin E, van Leeuwen J, Mair B, Moffat J, Boone C, and Andrews B (2019). Global genetic networks and the genotype-to-phenotype relationship. Cell 177, 85–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costanzo M, VanderSluis B, Koch EN, Baryshnikova A, Pons C, Tan G, Wang W, Usaj M, Hanchard J, Lee SD, et al. (2016). A global genetic interaction network maps a wiring diagram of cellular function. Science 353, aaf1420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costello JL, Castro IG, Hacker C, Schrader TA, Metz J, Zeuschner D, Azadi AS, Godinho LF, Costina V, Findeisen P, et al. (2017). ACBD5 and VAPB mediate membrane associations between peroxisomes and the ER. J. Cell Biol. 216, 331–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster JM, Rossen J, Kazachkova M, Pan J, Kugener G, Root DE, and Tsherniak A (2019). Extracting biological insights from the Project Achilles genome-scale CRISPR screens in cancer cell lines. bioRxiv https://www.biorxiv.org/content/10.1101/720243v1.
- Drew K, Wallingford JB, and Marcotte EM (2020). hu.MAP 2.0: Integration of over 15,000 proteomic experiments builds a global compendium of human multiprotein assemblies. Mol. Syst. Biol. 17, e10016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudley AM, Janse DM, Tanay A, Shamir R, and Church GM (2005). A global view of pleiotropy and phenotypically derived gene function in yeast. Mol. Syst. Biol. 1, 2005.0001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elad M (2010). Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing, 2010th Edition (Springer Science and Business Media; ). [Google Scholar]
- Elrod ND, Henriques T, Huang KL, Tatomer DC, Wilusz JE, Wagner EJ, and Adelman K (2019). The integrator complex attenuates promoter-proximal transcription at protein-coding genes. Mol. Cell 76, 738–752.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer B, Sandmann T, Horn T, Billmann M, Chaudhary V, Huber W, and Boutros M (2015). A map of directional genetic interactions in a metazoan cell. eLife 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser AG, and Marcotte EM (2004). A probabilistic view of gene function. Nat. Genet. 36, 559–564. [DOI] [PubMed] [Google Scholar]
- Gardini A, Baillat D, Cesaroni M, Hu D, Marinis JM, Wagner EJ, Lazar MA, Shilatifard A, and Shiekhattar R (2014). Integrator regulates transcriptional initiation and pause release following activation. Mol. Cell 56, 128–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Go CD, Knight JDR, Rajasekharan A, Rathod B, Hesketh GG, Abe KT, Youn JY, Samavarchi-Tehrani P, Zhang H, Zhu LY, et al. (2021). A proximity-dependent biotinylation map of a human cell. Nature 595, 120–124. [DOI] [PubMed] [Google Scholar]
- Gonçalves E, Segura-Cabrera A, Pacini C, Picco G, Behan FM, Jaaks P, Coker EA, van der Meer D, Barthorpe A, Lightfoot H, et al. (2020). Drug mechanism-of-action discovery through the integration of pharmacological and CRISPR screens. Mol. Syst. Biol. 16, e9405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gratten J, and Visscher PM (2016). Genetic pleiotropy in complex traits and diseases: Implications for genomic medicine. Genome Med 8, 78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart T, Chandrashekhar M, Aregger M, Steinhart Z, Brown KR, MacLeod G, Mis M, Zimmermann M, Fradet-Turcotte A, Sun S, et al. (2015). High-resolution CRISPR screens reveal fitness genes and genotype-specific cancer liabilities. Cell 163, 1515–1526. [DOI] [PubMed] [Google Scholar]
- Henkel L, Rauscher B, and Boutros M (2019). Context-dependent genetic interactions in cancer. Curr. Opin. Genet. Dev. 54, 73–82. [DOI] [PubMed] [Google Scholar]
- Hesketh GG, Papazotos F, Pawling J, Rajendran D, Knight JDR, Martinez S, Taipale M, Schramek D, Dennis JW, and Gingras AC (2020). The GATOR–Rag GTPase pathway inhibits mTORC1 activation by lysosome-derived amino acids. Science 370, 351–356. [DOI] [PubMed] [Google Scholar]
- Hou L, Wang Y, Liu Y, Zhang N, Shamovsky I, Nudler E, Tian B, and Dynlacht BD (2019). Paf1C regulates RNA polymerase II progression by modulating elongation rate. Proc. Natl. Acad. Sci. USA 116, 14583–14592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hua R, Cheng D, Coyaud É, Freeman S, Di Pietro E, Wang Y, Vissa A, Yip CM, Fairn GD, Braverman N, et al. (2017). VAPs and ACBD5 tether peroxisomes to the ER for peroxisome maintenance and lipid homeostasis. J. Cell Biol. 216, 367–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hustedt N, Álvarez-Quilón A, McEwan A, Yuan JY, Cho T, Koob L, Hart T, and Durocher D (2019). A consensus set of genetic vulnerabilities to ATR inhibition. Open Biol 9, 190156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kairov U, Cantini L, Greco A, Molkenov A, Czerwinska U, Barillot E, and Zinovyev A (2017). Determining the optimal number of independent components for reproducible transcriptomic data analysis. BMC Genomics 18, 712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling DM, Garza P, Nartey CM, and Carvunis AR (2019). The meanings of “function” in biology and the problematic case of de novo gene emergence. eLife 8, e47014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim E, Dede M, Lenoir WF, Wang G, Srinivasan S, Colic M, and Hart T (2019). A network of human functional gene interactions from knockout fitness screens in cancer cells. Life Sci. Alliance 2, e201800278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim E, Gheorge V, and Hart T (2021). Dynamic rewiring of biological activity across genotype and lineage revealed by context-dependent functional interactions. bioRxiv. 10.1101/2021.06.25.450004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H, and Park H (2007). Sparse non-negative matrix factorizations via alternating non-negativity-constrained least squares for microarray data analysis. Bioinformatics 23, 1495–1502. [DOI] [PubMed] [Google Scholar]
- Kinsler G, Geiler-Samerotte K, and Petrov DA (2020). Fitness variation across subtle environmental perturbations reveals local modularity and global pleiotropy of adaptation. eLife 9, e61271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch EN, Costanzo M, Deshpande R, Andrews B, Boone C, and Myers CL (2017). Systematic identification of pleiotropic genes from genetic interactions. bioRxiv. 10.1101/112326. [DOI] [Google Scholar]
- Kramer M, Dutkowski J, Yu M, Bafna V, and Ideker T (2014). Inferring gene ontologies from pairwise similarity data. Bioinformatics 30, i34–i42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lightfoot HL, Hagen T, Cléry A, Allain FH-T, and Hall J (2018). Control of the polyamine biosynthesis pathway by G2-quadruplexes. eLife 7, e36362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loregger A, Raaben M, Nieuwenhuis J, Tan JME, Jae LT, van den Hengel LG, Hendrix S, van den Berg M, Scheij S, Song JY, et al. (2020). Haploid genetic screens identify Spring/C12ORF49 as a determinant of SREBP signaling and cholesterol metabolism. Nat. Commun. 11, 1128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mairal J, Bach F, and Ponce J (2014). Sparse modeling for image and vision processing. arXiv, 1411.3230v2. [Google Scholar]
- Malovannaya A, Li Y, Bulynko Y, Jung SY, Wang Y, Lanz RB, O’Malley BW, and Qin J (2010). Streamlined analysis schema for high-throughput identification of endogenous protein complexes. Proc. Natl. Acad. Sci. USA 107, 2431–2436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mascibroda LG, Shboul M, Elrod ND, Colleaux L, Hamamy H, Huang K-L, Peart N, Singh MK, Lee H, Merriman B, et al. (2020). INTS13 mutations causing a developmental ciliopathy disrupt integrator complex assembly. bioRxiv. 10.1101/2020.07.20.209130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mashtalir N, D’Avino AR, Michel BC, Luo J, Pan J, Otto JE, Zullow HJ, McKenzie ZM, Kubiak RL, St Pierre R, et al. (2018). Modular organization and assembly of SWI/SNF family chromatin remodeling complexes. Cell 175, 1272–1288.e20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonald ER 3rd, de Weck A, Schlabach MR, Billy E, Mavrakis KJ, Hoffman GR, Belur D, Castelletti D, Frias E, Gampa K, et al. (2017). Project DRIVE: A compendium of cancer dependencies and synthetic lethal relationships uncovered by large-scale, deep RNAi screening. Cell 170, 577–592.e10. [DOI] [PubMed] [Google Scholar]
- McInnes L, Healy J, and Melville J (2018). UMAP: Uniform manifold approximation and projection for dimension reduction. arXiv, 1802.03426. [Google Scholar]
- Meyers RM, Bryan JG, McFarland JM, Weir BA, Sizemore AE, Xu H, Dharia NV, Montgomery PG, Cowley GS, Pantel S, et al. (2017). Computational correction of copy-number effect improves specificity of CRISPR-Cas9 essentiality screens in cancer cells. Nat. Genet. 49, 1779–1784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michel BC, D’Avino AR, Cassel SH, Mashtalir N, McKenzie ZM, McBride MJ, Valencia AM, Zhou Q, Bocker M, Soares LMM, et al. (2018). A non-canonical SWI/SNF complex is a synthetic lethal target in cancers driven by BAF complex perturbation. Nat. Cell Biol. 20, 1410–1420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikolov T, Yih W-T, and Zweig G (2013). Linguistic regularities in continuous space word representations. In Proceedings of the 2013 conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (Association for Computational Linguistics), pp. 746–751. [Google Scholar]
- Norman TM, Horlbeck MA, Replogle JM, Ge AY, Xu A, Jost M, Gilbert LA, and Weissman JS (2019). Exploring genetic interaction manifolds constructed from rich single-cell phenotypes. Science 365, 786–793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olivieri M, Cho T, Álvarez-Quilón A, Li K, Schellenberg MJ, Zimmermann M, Hustedt N, Rossi SE, Adam S, Melo H, et al. (2020). A genetic map of the response to DNA damage in human cells. Cell 182, 481–496.e21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan J, Meyers RM, Michel BC, Mashtalir N, Sizemore AE, Wells JN, Cassel SH, Vazquez F, Weir BA, Hahn WC, et al. (2018). Interrogation of mammalian protein complex structure, function, and membership using genome-scale fitness screens. Cell Syst 6, 555–568, e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pennington J, Socher R, and Manning CD (2014). Glove: Global vectors for word representation. In Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP), pp. 1532–1543. [Google Scholar]
- Pfleiderer MM, and Galej WP (2021). Structure of the catalytic core of the Integrator complex. Mol. Cell 81, 1246–1259.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price MN, Wetmore KM, Waters RJ, Callaghan M, Ray J, Liu H, Kuehl JV, Melnyk RA, Lamson JS, Suh Y, et al. (2018). Mutant phenotypes for thousands of bacterial genes of unknown function. Nature 557, 503–509. [DOI] [PubMed] [Google Scholar]
- Rancati G, Moffat J, Typas A, and Pavelka N (2018). Emerging and evolving concepts in gene essentiality. Nat. Rev. Genet. 19, 34–49. [DOI] [PubMed] [Google Scholar]
- Raudvere U, Kolberg L, Kuzmin I, Arak T, Adler P, Peterson H, and Vilo J (2019). g:profiler: A web server for functional enrichment analysis and conversions of gene lists (2019 update). Nucleic Acids Res 47, W191–W198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinstein R, Bruckstein AM, and Elad M (2010). Dictionaries for sparse representation modeling. Proc. IEEE 98, 1045–1057. [Google Scholar]
- Sabath K, Stäubli ML, Marti S, Leitner A, Moes M, and Jonas S (2020). INTS10-INTS13-INTS14 form a functional module of Integrator that binds nucleic acids and the cleavage module. Nat. Commun. 11, 3422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanson KR, Hanna RE, Hegde M, Donovan KF, Strand C, Sullender ME, Vaimberg EW, Goodale A, Root DE, Piccioni F, et al. (2018). Optimized libraries for CRISPR-Cas9 genetic screens with multiple modalities. Nat. Commun. 9, 5416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekelsky JJ, Burtis KC, and Hawley RS (1998). Damage control: The pleiotropy of DNA repair genes in Drosophila melanogaster. Genetics 148, 1587–1598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solovieff N, Cotsapas C, Lee PH, Purcell SM, and Smoller JW (2013). Pleiotropy in complex traits: Challenges and strategies. Nat. Rev. Genet. 14, 483–495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spedale G, Timmers HTM, and Pijnappel WWMP (2012). ATAC-king the complexity of Saga during evolution. Genes Dev 26, 527–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadelmayer B, Micas G, Gamot A, Martin P, Malirat N, Koval S, Raffel R, Sobhian B, Severac D, Rialle S, et al. (2014). Integrator complex regulates NELF-mediated RNA polymerase II pause/release and processivity at coding genes. Nat. Commun. 5, 5531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein-O’Brien GL, Arora R, Culhane AC, Favorov AV, Garmire LX, Greene CS, Goff LA, Li Y, Ngom A, Ochs MF, et al. (2018). Enter the matrix: factorization uncovers knowledge from omics. Trends Genet 34, 790–805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szklarczyk D, Franceschini A, Wyder S, Forslund K, Heller D, Huerta-Cepas J, Simonovic M, Roth A, Santos A, Tsafou KP, et al. (2015). STRING v10: protein–protein interaction networks, integrated over the tree of life. Nucleic Acids Res 43, D447–D452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatomer DC, Elrod ND, Liang D, Xiao MS, Jiang JZ, Jonathan M, Huang KL, Wagner EJ, Cherry S, and Wilusz JE (2019). The integrator complex cleaves nascent mRNAs to attenuate transcription. Genes Dev 33, 1525–1538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tilley FC, Arrondel C, Chhuon C, Boisson M, Cagnard N, Parisot M, Menara G, Lefort N, Guerrera IC, Bole-Feysot C, et al. (2021). Disruption of pathways regulated by integrator complex in Galloway-Mowat syndrome due to WDR73 mutations. Sci. Rep. 11, 5388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai KL, Tomomori-Sato C, Sato S, Conaway RC, Conaway JW, and Asturias FJ (2014). Subunit architecture and functional modular rearrangements of the transcriptional mediator complex. Cell 157, 1430–1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsherniak A, Vazquez F, Montgomery PG, Weir BA, Kryukov G, Cowley GS, Gill S, Harrington WF, Pantel S, Krill-Burger JM, et al. (2017). Defining a cancer dependency map. Cell 170, 564–576.e16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyler AL, Crawford DC, and Pendergrass SA (2016). The detection and characterization of pleiotropy: Discovery, progress, and promise. Brief. Bioinform. 17, 13–22. [DOI] [PubMed] [Google Scholar]
- Wagner GP, and Zhang J (2011). The pleiotropic structure of the genotype-phenotype map: The evolvability of complex organisms. Nat. Rev. Genet. 12, 204–213. [DOI] [PubMed] [Google Scholar]
- Wainberg M, Kamber RA, Balsubramani A, Meyers RM, Sinnott-Armstrong N, Hornburg D, Jiang L, Chan J, Jian R, Gu M, et al. (2021). A genome-wide atlas of co-essential modules assigns function to uncharacterized genes. Nat. Genet. 53, 638–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T, Yu H, Hughes NW, Liu B, Kendirli A, Klein K, Chen WW, Lander ES, and Sabatini DM (2017). Gene essentiality profiling reveals gene networks and synthetic lethal interactions with oncogenic Ras. Cell 168, 890–903.e15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Liao BY, and Zhang J (2010). Genomic patterns of pleiotropy and the evolution of complexity. Proc. Natl. Acad. Sci. USA 107, 18034–18039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe K, Stringer S, Frei O, Umićević Mirkov M, de Leeuw C, Polderman TJC, van der Sluis S, Andreassen OA, Neale BM, and Posthuma D (2019). A global overview of pleiotropy and genetic architecture in complex traits. Nat. Genet. 51, 1339–1348. [DOI] [PubMed] [Google Scholar]
- Xiao J, Xiong Y, Yang LT, Wang JQ, Zhou ZM, Dong LW, Shi XJ, Zhao X, Luo J, and Song BL (2021). POST1/C12ORF49 regulates the SREBP pathway by promoting site-1 protease maturation. Protein Cell 12, 279–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yankelevsky Y, and Elad M (2016). Dual graph regularized dictionary learning. IEEE Trans. Signal Inf. Process. Over Netw. 2, 611–624. [Google Scholar]
- Yankelevsky Y, and Elad M (2020). Theoretical guarantees for graph sparse coding. Appl. Comput. Harmon. Anal. 49, 698–725. [Google Scholar]
- Zhang J, Chen Y, Cheung B, and Olshausen BA (2019). Word embedding visualization via dictionary learning. arXiv, 1910.03833. [Google Scholar]
- Zheng H, Qi Y, Hu S, Cao X, Xu C, Yin Z, Chen X, Li Y, Liu W, Li J, et al. (2020). Identification of Integrator-PP2A complex (INTAC), an RNA polymerase II phosphatase. Science 370, eabb5872. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table. All other data reported in this paper will be shared by the lead contact upon request.
Key resources table.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| HA | Cell Signaling Technology | 2367S |
| INTS10 | Abcam | ab180934 |
| C7orf26 | Novus | NBP2-14764 |
| INTS13 | Bethyl | A303-575A |
| INTS14 | Bethyl | A303-576A |
| INTS9 | Cell Signaling Technology | 13945S |
| INTS6 | Santa Cruz | sc-376524 |
| TBP | Abcam | ab51841 |
| Deposited data | ||
| Genotoxic fitness screens | http://durocherlab.org/datasets/ | https://doi.org/10.1016/j.cell.2020.05.040, Supplementary Table 2 |
| Cancer Dependency Map, 19Q4 release (fitness data for Webster input) | https://depmap.org/portal/ | https://doi.org/10.6084/m9.figshare.11384241.v3 |
| Cancer Dependency Map, 21Q2 release (omics data for biomarker pipeline) | https://depmap.org/portal/ | https://doi.org/10.6084/m9.figshare.14541774.v2 |
| PRISM Drug Repurposing data | https://doi.org/10.1038/s43018-019-0018-6 | https://doi.org/10.6084/m9.figshare.9393293.v4 |
| Human Cell Map (proximity ligation data) | 10.1038/s41586-021-03592-2 | 10.1038/s41586-021-03592-2 |
| Experimental models: Cell lines | ||
| 293FT | Thermo Fisher Scientific | R70007 |
| Oligonucleotides | ||
| INTS6 Avana gRNA (chr13_51452485_+): ATGGCTGCGCTGGTTCATAG | This paper | N/A |
| INTS10 Avana gRNA (chr8_19823975_−) : TCTTAAACAACCTCTCCCAA | This paper | N/A |
| C7orf26 Avana gRNA (chr7_6594465_+) : TTACTGTGTGAGGTTAGCCA | This paper | N/A |
| Recombinant DNA | ||
| lentiCRISPR v2-Blast | Addgene | 83480 |
| pLEX_307 | Addgene | 41392 |
| pLX_HA | This study | 178534 |
| pLX_HA-C7orf26v1 | This study | 178535 |
| pLX_HA-C7orf26v2 | This study | 178536 |
| pLX_317-C7orf26v1 | This study | 178537 |
| pLX_317-C7orf26v2 | This study | 178538 |
| Software and algorithms | ||
| R | R Foundation | https://www.r-project.org/ |
| MATLAB | Mathworks | https://www.mathworks.com/products/matlab.html |
| gProfiler | doi:10.1093/nar/gkz369 | https://biit.cs.ut.ee/gprofiler/ |
| DGRDL | 10.1109/TSIPN.2016.2605763 | https://elad.cs.technion.ac.il/software/ |
| gene_fn | This study | 10.5281/zenodo.5773076 |
| graph_dictionary_learning | Various open source codebases | 10.5281/zenodo.5773078 |
All original code has been deposited and is publicly available as of the date of publication. The main repository contains R code for reproducing figures and analyses presented in the paper and can be found at https://github.com/joshbiology/gene_fn (Zenodo archive: https://doi.org/10.5281/zenodo.5773076). We created a Figshare archive that is the starting point for these analyses (https://doi.org/10.6084/m9.figshare.14960006.v2). We provide a second repository of MATLAB code implementing the factorization methods that are the basis of Webster, which can be found at https://github.com/joshbiology/graph_dictionary_learning (Zenodo archive: https://doi.org/10.5281/zenodo.5773078). Finally, we provide a data repository containing Webster’s preprocessed numerical input data and subsequent analysis output, a subset of which form the Supplemental Tables cited throughout this paper (https://doi.org/10.6084/m9.figshare.14963561.v2).
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.