A Cardiac Shape Model for Segmentation Uncertainty Quantification

Abstract

Segmentation of cardiac images is a variable component of many patient specific computational pipelines, yet its impact on simulated results are still not fully understood. A hurdle to to exploring the impact of the segmentation variability is the technical challenge of building a statistical shape model of the ventricles. In this study, we improved open our previous shape analysis by creating a unified shape model including both the epicardium and endocardium. We tested four techniques within ShapeWorks to generate a ventricular shape model: standard, multidomain, hybrid multidomain, and geodesic distance. The multidomain and hybrid multidomain generated a shape model using all eleven segmentations, and the geodesic distance method generated a shape model using a subset of four segmentations. Each of the shape models captured spatially dependent characteristics of the segmentation variability, including wall thickness, annular diameter, and basal truncation. While each of the three methods have benefits, the hybrid multidomain approach provided the most accurate shape model with fewest points and may be most useful in a majority of applications.

1. Introduction

The growing relevance of patient-specific cardiac simulation as a research and clinical tool is a result of its promise to accurately predict arrhythmias and guid treatments. The prevailing simulation methods, such as heart propagation models [1], ECG forward simulation, and Electrocardiographic Imaging (ECGI)[2, 3], extract geometric and parametric data from clinical sources, especially medical images, into computer models. Although the emergence of many of these pipelines into clinical use is eminent, uncertainty from the variable interpretation of clinical inputs remains largely unquantified for many approaches.

The interpretation of clinical data into a tractable cardiac models requires a compilation of many assumptions and estimations, leading to multiple possible sources of uncertainty. One such source, often overlooked, is the segmentation of the geometric model, particularly the heart. Segmentation of cardiac images is largely viewed as a solved problem, yet it usually requires manual input and user judgements. We have previously shown that experts from multiple research groups generate segmentations of the the same patient geometry that vary widely, especially the cardiac surface [4]. This variability likely affects the ECGI solutions [5], and we have used statistical shape analysis to quantify the variability of segmentation of a patient geometry [6] and incorporate the statistical shape model an ECGI pipeline to quantify the uncertainty due to segmentation variability [7]. However, previous shape models did not incorporate the epicardium and the endocardium together, limiting their possible applications.

In this study, we improved open our previous shape analysis of ventricular segmentation variability by creating a unified shape space including both the epicardium and endocardium. We used the collaborative framework of the Consortium for ECG Imaging (CEI) to generate multiple segmentations of the same patient to provide sufficient data for computing shape variability of cardiac segmentations, and used a correspondence-based shape analysis to calculate shape statistics in a parameterized shape space. We found that multiple strategies enable the production of shape models that could be used in multiple cardiac simulation pipelines and with uncertainty quantification techniques.

2. Methods

We used the statistical shape analysis on multiple segmentations to quantify the segmentation variability of patient. Researchers within the Consortium for ECG Imaging (CEI, ecg-imaging.org), supplied eleven ventricular segmentations from a single patient CT scan and ShapeWorks [8] (https://www.sci.utah.edu/software/shapeworks.html) was used to compute correspondence points on all surfaces then to compute the shape space for each set of correspondences using Principal Component Analysis (PCA). We employed four strategies within ShapeWorks to generate a unified shape model for use in cardiac simulation pipelines: standard, multidomain, hybrid multidomain, and geodesic distance.

ShapeWorks’ approach to shape analysis involves finding correspondence points across all input geometries using a particle system optimizer. The optimization attempts to maximize distance between points while minimizing the number of modes of variation across the cohort of geometries. In the standard application of ShapeWorks the segmentations of the heart, including both the endocardium and the epicardium, are used as a single region in the particle optimizer (Figure 1). Due to the relatively thin walls and concave geometry of the ventricles, ShapeWorks cannot always place correspondences consistently across segmentations. In the multidomain approach, the epicardium, left ventricular (LV) endocardium, and the right ventricular (RV) endocardium are separated into three domains which are optimized simultaneously, but each domain uses separate correspondances. This approach utilizes the mostly convex shapes of each of the surfaces to improve correspondence optimization. The hybrid multidomain approach uses the same three domains as multidomain, but the domains are optimized separately, then a single shape space is generated from the PCA. The advantage of this strategy over multidomain is a simplified parameter set for the ShapeWorks optimization, yet this approach doesn’t necessarily minimize the axes of variation for the unified space. The final approach used in this study uses geodesic distance, or distance along the surface, instead of euclidean distance in the particle optimization, allows the algorithm to better differentiate endocardium and epicardium points. Each of the four strategies were evaluated qualitatively, and by the variability captured with each axis.

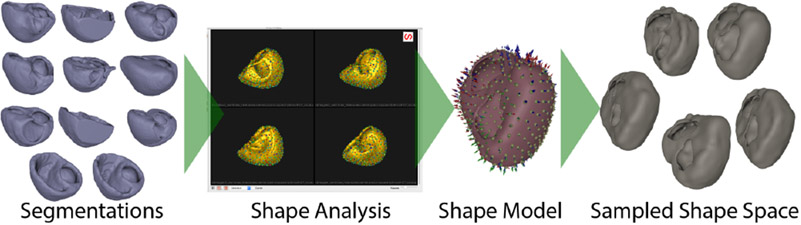
Figure 1.

Shape analysis pipeline. ShapeWorks generates the shape model, which can be used in simulation pipelines.

The medical images used in this study were collected by Sapp et al. [9] and are available for open use on the EDGAR database (http://edgar.sci.utah.edu) [10] a shared resource of the CEI.

3. Results

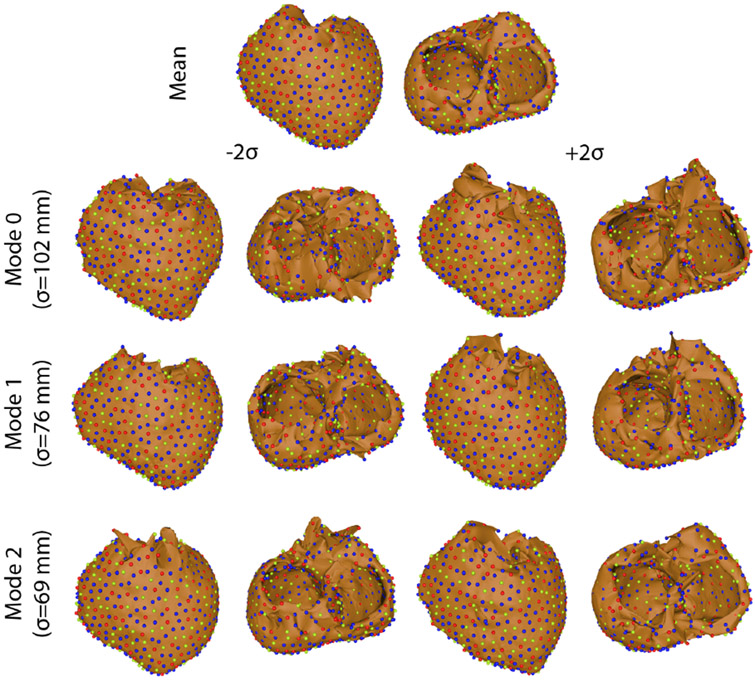
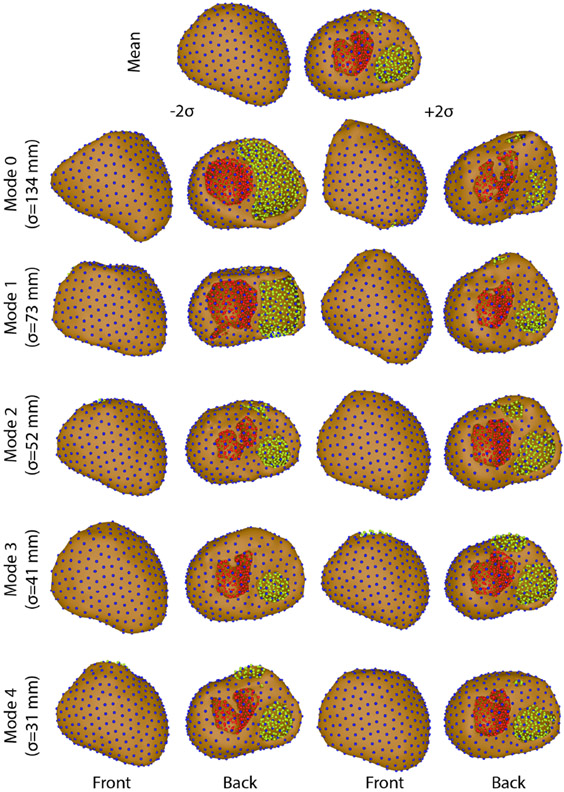
The four ShapeWorks strategies tested in this study displayed varied levels of success in generating shape models of segmentation variability (Figures 2, 3, 4, & 5). Only multidomain and hybrid multidomain were able to generate a coherent shape model with all eleven segmentations. The geodesic distance strategy was able to generate a shape model by using a subset of four segmentations that were most similar. The standard approach did not generate coherent correspondences nor a sensible shape model from the full set or a subset of the segmentations. Shape models generated by the multidomain (Figure 3), hybrid multidomain (Figure 4), and the geodesic distance methods (Figure 5) each captured similar spatially dependent characteristics of the segmentation variability, including wall thickness, annular diameter, and basal truncation. Each of these three methods had difficulty capturing the thin walls of the ventricles in the extremes of the shape space (±2σ). However, each axis avoided holes or crossing wall surfaces ≤ ∣1.5σ∣. Shape models generated from the multidomain and hybrid multidomain also captured variable valve openings within the shape space (Figures 3 & 4).

Figure 2.

Variation on each mode of variation using the standard method.

Figure 3.

Variation on each mode of variation using the multidomain method.

Figure 4.

Variation on each mode of variation using the hybrid multidomain method.

Figure 5.

Variation on each mode of variation using the geodesic distance method.

The total variability of the shape models generated by each of the four methods varied in magnitude and distribution. The total variation captured by each method was: 21,000 mm² standard, 30,700mm² multidomain, 18,200 mm² hybrid multidomain, and 6,200 mm² geodesic distance. The standard and geodesic distance required three modes capture 90% of the total variability of the model. An important note is that three was the maximum number of possible modes of variation because these shape models used only four input segmentations. The multidomain and hybrid multidomain methods generated shape models that captured 92% of the total variability with 5 modes of variation (with 10 total modes). The total variation captured by the standard approach was more than 3 times higher than the variability captured by geodesic distance. This discrepancy is likely from artificial variation from poor correspondences in the standard model. Similarly, the multidomain approach also captured nearly double the total variation captured by the hybrid multidomain approach. An important note is that the multidomain approach required more correspondences than the hybrid multidomain (1,536 compared to 1,024), which likely caused much of the difference in the total variation between the two methods.

4. Discussion and Conclusions

The results of this study provide support for three different techniques to use ShapeWorks to generated unified shape models of ventricular segmentation variability. Additionally, we demonstrated that computation meshes can be generated from these shape models, although the utility of the meshes from each method may be application specific.

The multidomain and hybrid multidomain approaches were far more versatile in their use of input data than the geodesic distance method. The use of the full set of supplied segmentations enable ShapeWorks to capture a wider range of variability, such a variable number of valve annuli, with greater accuracy. However, the geodesic distance method provided a model with a constant number of correspondence points in contact with the ventricular surface; a feature that simplifies registration, mesh warping, and other applications. However, despite reducing the input data for the geodesic distance method, it was much more computationally expensive and much more challenging to find the appropriate ShapeWorks parameters than the multidomain and hybrid multidomain approaches. Furthermore, the multidomain and hybrid multidomain approaches generated more consistent correspondence points and were more qualitatively accurate.

We have created unified ventricular shape models capturing segmentation variability of a patient using ShapeWorks with three techniques. While each of the three methods have benefits, the hybrid multidomain approach provided the most accurate shape model with fewest points, which is likely to be most useful in a majority of applications. These shape models will be instrumental in estimating the effect of segmentation variability on the uncertainty of cardiac modeling pipelines of different types, including isolated heart models and ECG forward simulations.