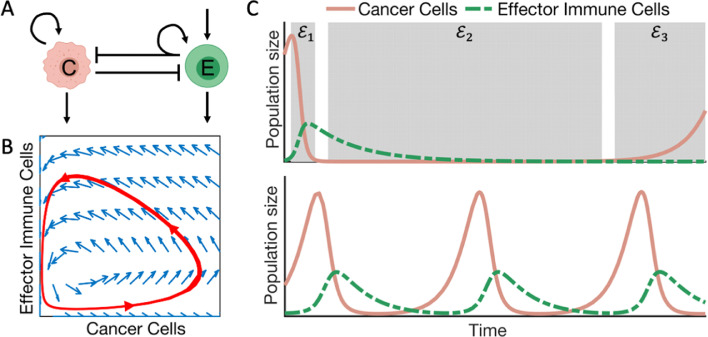
Fig. 2.

The dynamics of a predator-prey type model of cancer-effector immune interactions.A) Model schematic. Cancer cells (C) proliferate, (curved returning arrow), and die (outgoing arrow). Effector cells (E) are recruited (incoming arrow) and die (outgoing arrow). The interactions between cancer cells and effector immune cells are inhibitory, denoted by the blunt arrow. Inhibition of cancer cells by effector cells recruits more immune cells (curved, returning arrow). B) The phase-plane of the model in (A). The red trajectory illustrates how the two populations change with regards to each other. Starting from the bottom left, the cancer cells increase in number while effector cells are recruited. Once the inhibitory effect exerted by effector cells is larger than the replacement of cancer cells, the trajectory moves towards the vertical axis. At this point the effector population is unsustainable by the cancer cell population and experiences a rapid decline, and the trajectory moves towards the horizontal axis. These oscillations continue indefinitely. C) Two solutions of the model in (A). Top panel, this model can recapitulate the three E's of immunoediting postulated by Dunn et al. [80]: elimination (${\epsilon }_1$), equilibrium (${\epsilon }_2$) and escape (${\epsilon }_3$). Bottom panel, solutions showing the explicit oscillatory behavior described in (B).