FIG 2.

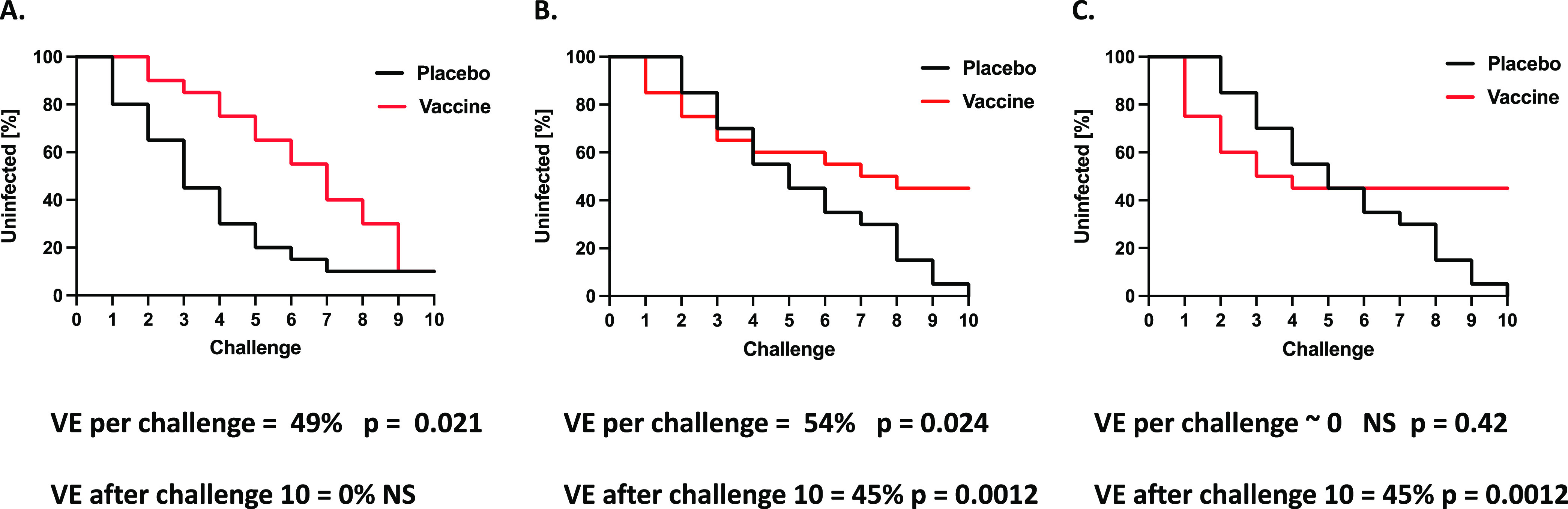
Different bases for calculation of vaccine efficacy. In experimental animal models of HIV-1 infection with iterated viral challenges, the diminishing fraction of uninfected animals can be presented in Kaplan-Meier plots. The remaining fraction of uninfected subjects over time can be similarly plotted in clinical trials. A log rank test can determine whether protection was significant in the vaccine group compared with the placebo controls (P values). Vaccine efficacy (VE) can be calculated for the entire curve based on log-rank hazard ratios. Alternatively, VE can be based on the fractions of uninfected subjects at a particular time, e.g., at the last challenge or early and late after vaccination (2, 51, 168). The significance of the difference between the placebo and vaccine recipients can then be determined by Fisher’s exact test. The Kaplan-Maier plots for simulated data in panels A, B, and C illustrate how the two methods can yield widely divergent VE values. In panel A, the protection per challenge is significant but VE = 0 at the end of the experiment (challenge-10). Similarly to this simulated example, in one macaque vaccine experiment with Ad26-SIV Env/Gag/Pol prime and SIV Env gp140 boost, the VE for the pool of vaccinated macaques was substantial and significant on a per-challenge basis (57%, log rank hazard ratios; P = 0.02), whereas there was no significant efficacy after 6 challenges (13%, P = 1.0, Fisher’s exact test; note that these are our calculations for the pool of vaccine recipients, which was not compared with control animals in the original study [31]). In panel B, VE per challenge is significant and somewhat greater than that in panel A, but the major difference is that it remains substantial after challenge-10. In panel C, VE per challenge is nonsignificant but VE after challenge-10 is substantial and equal to that in panel B.