Magnetic properties of 3d transition metal (Sc–Ni) doped plumbene

Abstract

Recently, a synthesized two-dimensional layer structured material, so-called “plumbene”, has attracted research interests because of its sizeable spin–orbit coupling. To study the potential of this material as a dilute magnetic semiconductor, we computationally investigate the structure, electronic, and magnetic properties of 3d transition metal (TM) doped plumbene using density functional theory (DFT). These calculations show that Ti, V, Cr, Mn, Fe, and Co-doped plumbene systems are magnetic while no magnetic solution was found for Sc and Ni. We also calculate the magnetic couplings between two TM impurities in the system with an impurity concentration of less than 2%. For V, Mn, Fe, Co-doped systems with short inter-impurity distances, we obtain a Curie temperature above room temperature using the mean-field approximation, indicating the potential for magnetic storage and spintronics applications.

Distance dependent exchange coupling between two transition metal (TM) impurities doped in plumbene in sites along the zigzag (z_i) and the armchair (a_j) directions.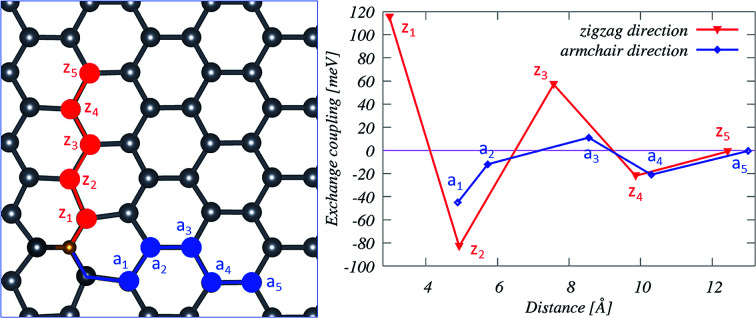

I. Introduction

Two-dimensional (2D) materials, particularly those in group 14, have attracted extensive interest due to their potential in terms of the topological insulating properties,^1–8 the chemical reactivity,⁹ the magnetic behavior,^10,11 and the thermal properties.¹² A recently synthesized 2D material, called plumbene^13–17 has generated much attention because it has the largest spin–orbit interaction among all group 14 elements¹⁸ as the magnitude of spin–orbit coupling increases approximately as the fourth power of the effective nuclear charge. Moreover, rich physical characteristics are expected in plumbene due to strong spin–orbit coupling (SOC) as compared to graphene and phosphorene,¹⁸i.e. huge host-induced magnetic anisotropy of impurities due to its strong SOC. In terms of mechanical properties, a recent molecular dynamics simulation has shown that plumbene is several times stronger than bulk lead.¹⁷ In terms of topological insulating properties, plumbene becomes a topological insulator with a large band gap (≈200 meV) through electron doping as shown by ab initio calculations.¹⁵ According to theoretical calculations, plumbene is also a good candidate for realizing the quantum spin Hall effect at room temperature (RT).¹⁹ Unexpected quantum spin Hall insulating properties were also reported for bilayer and decorated plumbene.^20,21

Over the past decades, there have been many studies regarding the fundamental science of dilute magnetic semiconductors (DMSs).^22–26 It has been shown that the combination of 2D semiconductors and magnetic data storage could lead to 2D spintronics devices with a wide range of applications such as nonvolatile magnetoresistive memories, spin valve, spin-based transistors, and magnetically enhanced optoelectronics devices.²⁷

The electronic and magnetic properties of 2D materials can be engineered with substitutional doping or adsorbing of TM elements, which can lead to DMSs in 2D semiconductors.^28–34 The magnetic substitutional doping can induce the spin and valley polarization due to the spin–orbit and exchange interaction in transition-metal dichalcogenides (TMDs).³⁵

In this paper, inspired by the recent synthesis of plumbene,¹³ we use 3d TM elements as magnetic impurities to show that it is possible to achieve magnetism in plumbene. First, we study the stability and electronic properties of TM defects in plumbene, and thereafter, the magnetic orders are acquired through the long-range interaction between the diluted TM-doped systems. The Curie temperature is also estimated using the mean-field approximation for the ferromagnetic (FM) cases.

II. Computational details

The calculations were performed within the framework of spin-polarized density functional theory (DFT) including SOC, using the Vienna ab initio simulation package (VASP).^36,37 SOC has a huge impact on the electronic properties of plumbene in such a way that without taking it into account, the global band gap disappears.¹⁶ The frozen-core full-potential projector augmented-wave method (PAW) was used³⁸ with the Perdew, Burke, and Ernzerhof (PBE)³⁹ generalized gradient approximation (GGA). These functionals provide a reasonably good description of the magnetic states of TM nanostructures such as adatoms^40,41 and nanowires.^42–44

The convergence with respect to the size of k-sampling, cutoff radius, and vacuum thickness was checked. These resulted in a k-point mesh of 2 × 2 × 1 for Density of States (DOS) of the TM-doped system, a plane-wave cutoff radius of 600 eV, and a vacuum distance between the periodic images of 15 Å. We used the conjugate-gradient algorithm for structural relaxation with a force convergence criterion of 0.01 eV Å⁻¹.

The pristine plumbene structure was fully optimized. To obtain the fundamental band gap, the electronic band structures were calculated by the PBE functional, hybrid Heyd–Scuseria–Ernzerhof functionals (HSE03)^45–47 and (HSE06).⁴⁸ We used the standard values for the mixing parameter (0.25) and the range-separation parameters of 0.3 Å⁻¹ and 0.2 Å⁻¹ for HSE03 and HSE06 functionals, respectively. Charge transfer analysis between TM and plumbene was carried out using Bader formalism.^49–51 The reciprocal space was sampled by a 6 × 6 × 1 k-points mesh in the Brillouin zone of the primitive unit cell. The electronic and magnetic properties of TM-doped systems were studied using the PBE-optimized structures. We used noncollinear spin polarization in a fully relativistic framework for the TM-doped plumbene systems to determine the easy magnetization axis and to calculate the magnetic interaction between two TM impurities. The structures, charge densities, and magnetization densities were visualized using VESTA code.⁵²

III. Results and discussions

A. Structure and energetics

The calculated lattice constant of freestanding plumbene using PBE, HSE03, and HSE06 functionals, as shown on Table 1, are 4.93 Å, 4.88 Å, and 4.87 Å, respectively, which shows a good agreement between these methods. The calculated buckling heights obtained by PBE, HSE03, and HSE06 functionals are also 1.01 Å, 0.97 Å, and 0.97 Å, respectively.

Electronic band gap energy, lattice constant, and buckling height (h) of plumbene calculated with the PBE, HSE03, and HSE06 functionals.

System	PBE	HSE03	HSE06
Band gap (eV)	0.43	0.50	0.58
Lattice constant (Å)	4.93	4.88	4.87
h (Å)	1.01	0.97	0.97

The calculated band gap energies are 0.43 eV, 0.50 eV, and 0.58 eV using PBE, HSE03, and HSE06 functionals, respectively. The electronic band structures obtained by these methods are displayed in Fig. 1(d). It is known that PBE is expected to underestimate the band gap energies^53–55 which may be reflected in our calculations. HSE functionals are well-established and more accurate for describing electronic properties of 2D materials as compared to PBE, but they are computationally very expensive.⁵⁶ We expect the experimental band gap energy to be higher than the calculated PBE band gap of 0.43 eV.

Fig. 1. (a and b) Top and side views of buckled plumbene, respectively. The blue solid vectors indicate the primitive vectors. h is the vertical distance between the Pb planes. (c) First Brillouin zone with high-symmetry points. (d) Electronic band structures for plumbene calculated with the HSE06 (blue solid line), HSE03 (brown dotted line), and PBE (red dashed line) functionals.

We checked the reliability of the PBE calculations and found consistent results across the PBE and the HSE methods in terms of magnetic configurations of the Fe-doped system. Due to the high computational workload and the reasonable agreement with the PBE results, we did not perform a similar study with the HSE approach.

To model the single impurity TM-doped systems, we chose a 4 × 2 supercell along the zigzag and armchair directions, respectively. Thus, the PBE lattice constants of a = 19.74 Å and b = 17.09 Å were used. This corresponds to 31 Pb atoms in a TM atom in the supercell. To calculate the magnetic exchange coupling between the two TM impurities, a 7 × 4 supercell was chosen with lattice constants of a = 34.54 Å and b = 34.18 Å, which corresponds to 110 Pb atoms and two TM atoms in this supercell. For structural relaxations of the TM-doped system in this supercell, we used only the Γ point sampling of the Brillouin zone. We first test the equilibrium configuration of a pristine plumbene sheet. The equilibrium structure for pristine plumbene is shown in Fig. 1(a and b). As obtained by PBE calculations, the equilibrium lattice constant, Pb–Pb bond length, and buckling height were estimated to be 4.93 Å, 3.02 Å, and 1.01 Å, respectively, which are consistent with previous studies.^14–16

Table 2 lists the geometric and magnetic characters of the TM-substituted plumbene. Pb binding energy is also calculated as a reference system. The binding energy in our calculations is defined as follows:

E_b = E_Pb−Vac + E_TM − E_Pb−TM, 1

where, E_b, E_Pb–Vac, E_TM, and E_Pb–TM represent the binding energy, the total energy of plumbene with a single vacancy, the energy of an isolated TM impurity, and the total energy of the substitutional system, respectively. After full geometry relaxation, all TM impurities form strong bonding to plumbene with a single vacancy because the values of E_b are in the range of 1.7 eV and higher. The binding energy is close to that of phosphorene,²⁸ suggesting that the bonding strength of the TM impurities to plumbene is rather strong. Moreover, there is a general trend that binding energy has a minimum value at the middle of the 3d series indicating that the binding is weakest when the d shell is half-filled. A similar trend is seen for phosphorene.²⁸ TM–Pb bond length typically decreases from Sc to Ni as the atomic radius decreases, except for Cr and Fe, for which the binding drastically weakens. This trend is shown in Fig. 2. The bonding characteristics between TM and plumbene are also manifested in charge density difference (Fig. 3). The covalent bonds between Mn (Cr) and Pb are weak, especially compared to the early 3d TM elements. The charge transfer is mainly from TM to the neighboring Pb atoms for the early 3d TM elements up to Fe, then from Pb atoms to Co and Ni. This may be one of the reasons that charge density difference (Fig. 3) does not represent a strong bond between Ni and Pb. TM atoms bond with three Pb atoms, retaining some unpaired electrons, which eventually leads to magnetism. However, for the electrons of 3d orbitals more than five, it is more complicated.

Binding energy, optimized bond lengths, easy axis, absolute values of spin and orbital moments, charge transfers, energy difference between antiparallel (E↑↓) parallel (E↑↑) spins of the TM impurities sites along zigzag (z_i) and armchair (a_j) directions, and Curie temperatures for the FM configurations.

Dopant	Sc	Ti	V	Cr	Mn	Fe	Co	Ni	Pristine
E b (eV)	3.10	2.79	2.54	1.72	1.70	2.61	2.87	3.37	1.97
TM–Pb (Å)	2.92	2.80	2.79	2.85	3.02	2.69	2.53	2.50	3.02
Easy axis		x̂	x̂	ŷ	ẑ	ẑ	ẑ
|ms| (μB)		1.32	2.79	3.98	4.10	2.95	1.52
|mo| (μB)		0.18	0.32	0.04	0.04	0.49	0.22
TM charge transfer (e)	−1.09	−0.81	−0.50	−0.36	−0.37	−0.09	+0.04	+0.20
Pb charge transfer (e)	+0.35	+0.27	+0.16	+0.12	+0.14	+0.02	−0.01	−0.07
ΔE(z1) (meV)		115		−430	−576	523	175
T C (K)		445				2023	677
ΔE(z2) (meV)		−83	−125	−98	128	91	12
T C (K)					495	352	46
ΔE(z3) (meV)		57	24	22	43	−78	−18
T C (K)		220	93	85	166
ΔE(z4) (meV)		−22	−12	1	−34	24	18
T C (K)				4		93	70
ΔE(z5) (meV)		−1	−7	7	−5	−15	−16
T C (K)				27
ΔE(a1) (meV)		−45	−125	−78	101	77	17
T C (K)					391	298	66
ΔE(a2) (meV)		−12	34	−99	−23	−33	−70
T C (K)			132
ΔE(a3) (meV)		11	−34	−36	−34	13	14
T C (K)		43				50	54
ΔE(a4) (meV)		−21	−47	−41	12	18	−5
T C (K)					46	70
ΔE(a5) (meV)		−0.5	−9	−10	8	15	1
T C (K)					31	58	4

Fig. 2. Binding energies (red) and magnetic moments (blue) of the TM-doped plumbene system. The dotted lines between symbols are a guide to the eye.

Fig. 3. Charge density difference of plumbene doped by TM atoms with an isosurface value of 0.004e Å⁻³, where e is the elementary electron charge. Blue and red regions denote loss (depletion) and gain (accumulation) of charges, respectively.

Additionally, to check the thermal stability of TM-doped systems, we performed ab initio molecular dynamics (MD) simulations at RT. As an example, we focused on the Mn case as it has the lowest binding energy. These simulations showed that the structure of Mn-doped system does not collapse throughout the MD simulation at 300 K, and this system can maintain its structural integrity at this temperature. Since this stability was checked for the Mn case, TM-doped systems with higher binding energies are expected to be even more stable.

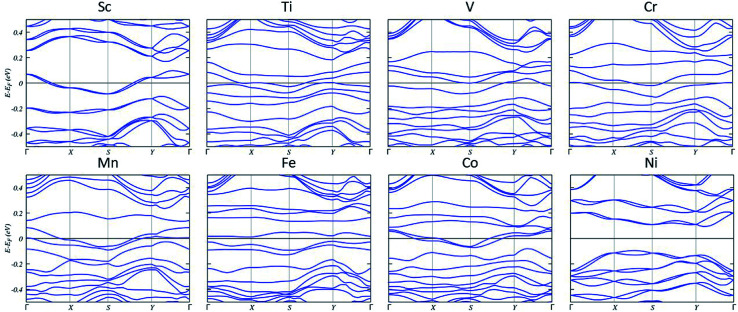
The calculated band structures (Fig. 4) of 3.1% concentration single TM-doped systems show that there are impurity states that cross the Fermi level. This indicates the metallic nature of TM-substituted systems with the exception of Fe and Ni. The band gaps are calculated to be 0.03 eV for Fe and 0.19 eV for Ni, respectively.

Fig. 4. Band structures of TM-doped plumbene systems. The fermi energy is set at zero.

The DOS and projected DOS (PDOS) of TM-doped systems (Fig. 5) show that the energy splitting between the TM 3d peaks is large, signifying that magnetism mainly originates from TM impurities. Several resonance peaks can be found in the DOS, which is caused by the strong hybridization between the 3d orbitals of TM and 3p orbitals of Pb.

Fig. 5. DOS and projected DOS of the TM-substituted systems. The Fermi level has been set to zero and indicated by a vertical gray dashed line.

B. Magnetic properties

First-principles calculations suggest that doping with Ti, V, Cr, Mn, Fe, and Co results in magnetic states, while no magnetic solutions are found for Sc and Ni-doped plumbene systems. Particularly, the impurities from V to Co have magnetic states due to more valence electrons than Pb and an open shell structure. Isolated transition metal atoms have a large spin and orbital magnetic moments according to Hund's rules. However, electron delocalization and crystal field effects compete with intra-atomic Coulomb interactions leading to an overall reduction of spin moments as well as quenching of orbital moments in TM impurities dissolved in nonmagnetic hosts. The absolute values of spin magnetic moments are 1.32 μ_B, 2.79 μ_B, 3.98 μ_B, 4.10 μ_B, 2.95 μ_B, and 1.52 μ_B for Ti, V, Cr, Mn, Fe, and Co, respectively, as shown in Table 2. Unlike graphene, plumbene doped with TM impurities has a fractional magnetic moment due to a partially occupied 4s orbital, which is unoccupied for TM-substituted graphene. The orbital magnetic moments of the TM-doped systems are 0.18 μ_B for Ti, 0.32 μ_B for V, 0.04 μ_B for Cr, 0.04 μ_B for Mn, 0.49 μ_B for Fe and 0.22 μ_B for Co, which display a minimum value at the middle of the 3d series.

The pd hybridization in TM-doped plumbene is characterized by long-range and anisotropic interactions between TM defects as listed on Table 2 and shown in Fig. 6. The TM impurity concentration is 1.79% in this case. The energy difference between parallel (E↑↑) and antiparallel spins (E↑↓) is exchange coupling. The spins are oriented along the corresponding preferential orientation (easy axis) in each case.

Fig. 6. (a) Schematic representation of TM impurity (yellow atom) doped in plumbene in sites along the zigzag (z_i) and the armchair (a_j) directions. (b) Energy differences between antiparallel (E↓↑) and parallel (E↑↑) spins as a function of the distance. The solid lines between symbols are a guide to the eye. z_i and a_j are noted on the Ti plot as an example.

For the nearest-neighbor interactions (z₁), spins align parallel for Ti, Fe, and Co and align antiparallel for Mn, Cr with the exchange couplings being very strong for Cr (−430 eV), Mn (−576 eV), and Fe (523 eV). Magnetic configurations of V could not be stabilized in this case. For the next nearest neighbor interaction (z₂ and a₁), spins align parallel for Mn, Fe, and Co and align antiparallel for Ti, V, and Cr. For the third and higher-order nearest-neighbor interactions, the inter-impurity exchange couplings of the TM across the plumbene oscillate and decay with the inter-impurity separation. These couplings are not typically strong. These positive and negative exchange couplings as a function of the distance lead to ferromagnetic (FM) and antiferromagnetic (AF) orderings. We note that the same magnetic orderings were obtained using the HSE methods for a Fe-doped system with a relatively short distance between the Fe impurities.

We chose the Mn-substituted system as a typical example, as shown in Fig. 7. These magnetic orders are shown by spin density oriented along the +z (blue) and the −z (red) directions, respectively. The spin density suggests that the magnetism originates from the TM atom, and the spin density is slightly induced in the nearest Pb atoms. There is a strong interaction for short distance between the two Mn atoms, resulting in orbital reconstruction, which causes no isolated unpaired electrons.

Fig. 7. Magnetization density for ground state systems consisting two Mn impurities doped in plumbene at sites along the zigzag (z_i) and the armchair (a_j) directions. The blue and red colors represent spin (oriented along the z and −z directions) densities with an isosurface value of 0.003 μ_B Å⁻³, where μ_B is the Bohr magneton.

It is worth noting that some metals, instead of substitutional doping, may tend to diffuse on 2D materials and form clusters.⁵⁷ In this case, an ensemble of single domain clusters or nanoparticles becomes a paramagnet as each independent particle has an effective magnetic moment which eventually leads to superparamagnetism.⁵⁸ This superparamagnet system behaves as an ensemble of non-interacting huge magnetic moments with no effective magnetic anisotropy.⁵⁹

C. Transition temperature

We can estimate the Curie temperature (T_C) in the mean-field approximation (MFA) via

2

where N_TM = 2 is the number of TM impurities in the supercell. T_C is a crucial parameter for the FM case.³⁰ For practical spintronics applications, the T_C must be higher than RT.

As listed on Table 2, the T_C above RT are estimated to be about 445 K for Ti (z₁), 495 K for Mn (z₂), 391 K for Mn (a₁), 2023 K for Fe (z₁), 352 K for Fe (z₂), 677 K for Co (z₁), respectively. These high T_Cs can be traced back to the high values of the exchange couplings for these systems.

To confirm the MFA results above, the T_C of Fe (z₂) was further determined using Monte Carlo (MC) simulations as it has the lowest T_C among the calculated T_Cs above RT. These simulations are used to evaluate the stability of 2D magnetic semiconducting^60–62 or conducting^43,63 systems.

T _C is primarily determined by the strength of the exchange coupling and influenced by the magnetic anisotropy energy (MAE). The latter is not taken into account by the MFA, but it is by the MC. In agreement with the Mermin–Wagner theorem,⁶⁴ we observed no magnetic ordering for a vanishing MAE. Introducing the MAE stabilizes the moments against thermal fluctuation and, thus, leads to a T_C.

The T_C was determined to be 300 K using the magnetic susceptibility with an MAE of 5.0 meV. The MFA overestimates the T_C by about 15%. Based on this calculation, a similar overestimation of T_C may be assumed for other TM-doped systems. This assumption does not decrease the T_Cs mentioned above to lower than RT. Our preliminary non-collinear DFT calculations suggest a colossal MAE for the TM-doped plumbene systems, which are significantly larger than 5.0 meV. An increase of the MAE will raise the T_C. Therefore even higher T_Cs are expected for these systems.

IV. Conclusions

Calculations within the DFT framework suggest that with a proper choice of TM doped in plumbene, we can control its electronic and magnetic properties. The spin polarization is found in Ti, V, Cr, Mn, Fe, and Co-doped systems. The long-range and anisotropic interactions between two TM impurities in plumbene with an impurity concentration of 1.79% were calculated. The Curie temperature above RT was estimated for Ti, Mn, Fe, and Co-doped systems, demonstrating the potential for spintronics applications.

Conflicts of interest

There are no conflicts to declare.