Sample size considerations for stepped wedge designs with subclusters

Abstract

The stepped wedge cluster randomized trial (SW-CRT) is an increasingly popular design for evaluating health service delivery or policy interventions. An essential consideration of this design is the need to account for both within-period and between-period correlations in sample size calculations. Especially when embedded in health care delivery systems, many SW-CRTs may have subclusters nested in clusters, within which outcomes are collected longitudinally. However, existing sample size methods that account for between-period correlations have not allowed for multiple levels of clustering. We present computationally efficient sample size procedures that properly differentiate within-period and between-period intracluster correlation coefficients in SW-CRTs in the presence of subclusters. We introduce an extended block exchangeable correlation matrix to characterize the complex dependencies of outcomes within clusters. For Gaussian outcomes, we derive a closed-form sample size expression that depends on the correlation structure only through two eigenvalues of the extended block exchangeable correlation structure. For non-Gaussian outcomes, we present a generic sample size algorithm based on linearization and elucidate simplifications under canonical link functions. For example, we show that the approximate sample size formula under a logistic linear mixed model depends on three eigenvalues of the extended block exchangeable correlation matrix. We provide an extension to accommodate unequal cluster sizes and validate the proposed methods via simulations. Finally, we illustrate our methods in two real SW-CRTs with subclusters.

1 |. INTRODUCTION

Stepped wedge cluster randomized trials (SW-CRTs) are an increasingly popular trial design for a variety of reasons including their potential benefits of increased power and statistical efficiency (Hemming and Taljaard, 2020). In an SW-CRT, one or more randomly allocated clusters are scheduled to transition from control to intervention at prespecified time points until all clusters are exposed to the intervention. Figure 1 provides a schematic of a typical SW-CRT in which eight clusters are allocated to four sequences and outcomes are observed within each of five time periods. SW-CRTs can employ either a cross-sectional or closed-cohort design, depending on whether repeated measurements are taken from the same or different individuals in each period.

FIGURE 1.

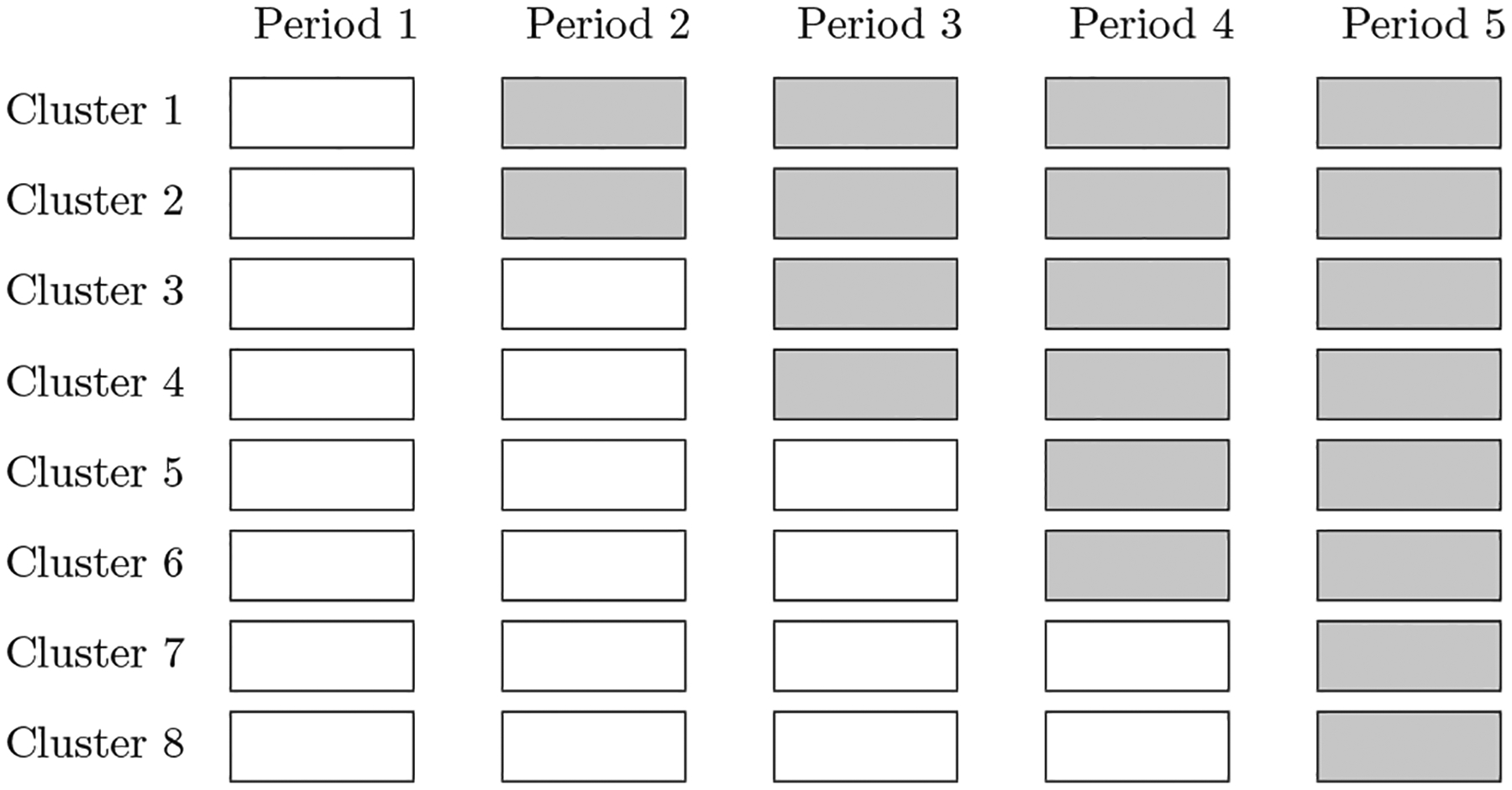
A schematic illustration of a SW-CRT with eight clusters and five periods. Each white cell indicates a cluster period under the control condition and each gray cell indicates a cluster period under the intervention condition. There are in total S = 4 distinct intervention sequences

A comprehensive methodological review of available statistical methods for SW-CRTs is presented in Li et al. (2021). While almost all current methods for designing SW-CRTs have assumed a two-level structure within periods (e.g., patients nested in practices), several recent trials have utilized data from patients nested within subclusters, giving rise to three-level structures within periods. For example, the Lumbar Imaging with Reporting of Epidemiology (LIRE) trial was an SW-CRT that evaluated the impact of inserting benchmark prevalence data in spinal imaging reports on subsequent health care utilization, and cross-sectionally sampled patients nested in primary care providers, who are nested in practices (Jarvik et al., 2015). As another example, the Washington State Expedited Partner Therapy (EPT) SW-CRT randomized local health jurisdictions (LHJ) consisting of clinics and cross-sectionally measured chlamydia infection in patients (Golden et al., 2015). In this paper, we present new methods for designing SW-CRTs that explicitly account for the three-level structure within each period while additionally accounting for the between-period correlation parameters.

For the standard parallel-arm CRT design (without repeated measures), Heo and Leon (2008) and Teerenstra et al. (2010) developed the design effect (DE) for three-level data with a Gaussian outcome. The DE is expressed as 1 + (N − 1)α₀ + N(K − 1)ρ₀, where α₀ and ρ₀ are the within-subcluster and between-subcluster intracluster correlation coefficients (ICCs), K and N are the number of subclusters and subcluster size, respectively. This DE represents the amount by which the sample size required for an individually randomized trial needs to be multiplied to obtain the sample size required for a three-level CRT and coincides with the leading eigenvalue of the nested exchangeable correlation structure (Li et al., 2019). The same DE expression also applies to three-level CRTs with a binary outcome (Teerenstra et al., 2010; Liu and Colditz, 2020). Frequently, it is assumed that the between-subcluster ICC does not exceed the within-subcluster ICC (Teerenstra et al., 2010), which suggests, based on the DE, that ρ₀ = α₀ would lead to conservative sample size estimates under parallel randomization.

The design and analysis of SW-CRTs have been conventionally based on linear mixed models (Li et al., 2021). Assuming a Gaussian outcome, Hemming et al. (2015) proposed a generic framework for designing cross-sectional SW-CRTs and extended the Hussey and Hughes (2007) linear mixed model by including an additional random intercept at the subcluster level. The variance of the intervention effect estimator was obtained using the covariance matrix of the generalized least squares estimator, but no analytical formulas were provided. Teerenstra et al. (2019) extended the Hemming et al. (2015) approach to accommodate closed-cohort SW-CRTs and developed closed-form DE expressions. However, these approaches implicitly assume that the between-period ICC equals the within-period ICC, both within and between subclusters. Under this strong assumption, we show in Section 3.1 that the variance of the intervention effect vanishes as the subcluster size grows indefinitely, which may lead to an underestimated sample size when the between-period ICCs differ from the within-period ICCs. To the best of our knowledge, explicit sample size formulas that differentiate between-period and within-period ICCs in SW-CRTs with multiple levels of clustering have not been previously derived. Furthermore, with a binary outcome, Teerenstra et al. (2019) considered an approximation based on a linear mixed model, which in the case of a single level of clustering has already been shown to be inaccurate (Zhou et al., 2020). To this end, it is necessary to develop more accurate sample size procedures that acknowledge the mean-variance relationship with a non-Gaussian outcome for multilevel SW-CRTs.

To address these issues, we consider a generalized linear mixed model (GLMM) that characterizes five possible sources of random variation in SW-CRTs with subclusters, while differentiating within-period and between-period ICCs. With a Gaussian outcome, we describe an extended block exchangeable correlation structure parameterized by at most five ICC parameters, depending on whether a cross-sectional or closed-cohort design is assumed at each level. We show in Section 3 that the variance of the intervention effect estimator depends on the ICCs only through two distinct eigenvalues of the extended block exchangeable correlation matrix. Although a scalar closed-form variance expression is unavailable for other exponential family outcomes, we propose a computationally efficient generic sample size algorithm based on cluster period averages. Under the canonical link functions, new strategies are provided to circumvent complex numerical integration. In addition, we also extend our approach to accommodate unequal cluster sizes. Our simulation studies to validate the proposed sample size methodology are presented in Section 4 and applications to two SW-CRTs with subclusters are presented in Section 5. Section 6 provides concluding remarks.

2 |. MODELS AND GENERIC SAMPLE SIZE CONSIDERATIONS

2.1 |. Three design variants

We consider a multilevel SW-CRT with I clusters and T periods, with subclusters nested in clusters and subjects nested in subclusters. We consider three possible variations of this multilevel stepped wedge design (Figure 2): (A) a closed-cohort design at both the subcluster and subject levels, in which case repeated measurements are taken on the same subjects in each subcluster over time; (B) a closed-cohort design on the subcluster level but a cross-sectional design at the subject level, in which case different subjects in the same subcluster are sampled at each time period; (C) a cross-sectional design at both the subcluster and subject level, in which case different subjects within different subclusters are sampled in each cluster during each period. Our development will include all three variants.

FIGURE 2.

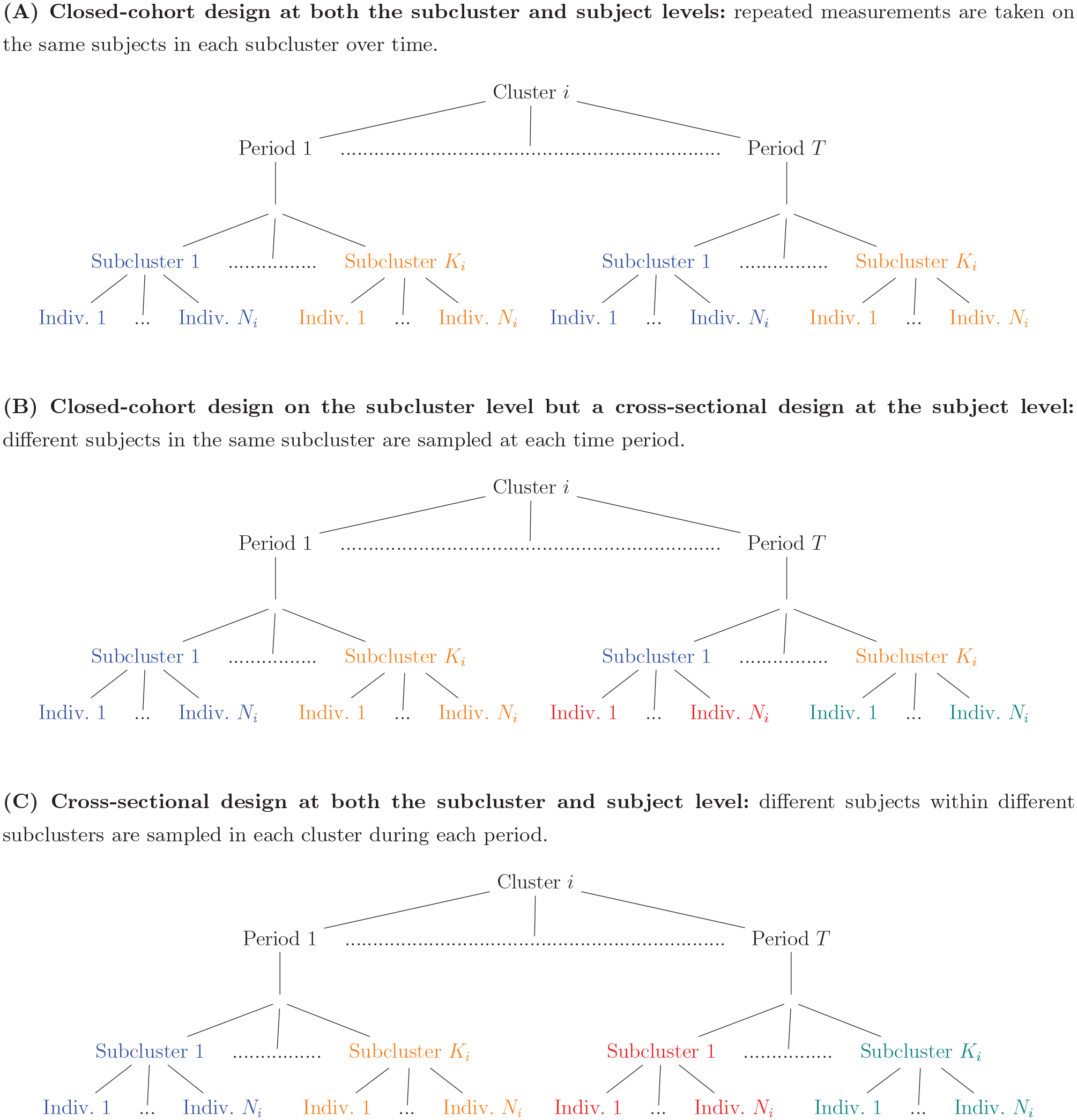
Three design variants for a multilevel SW-CRT with T periods, K_i subclusters per cluster, and N_i individuals (Indiv.) per subcluster. Colors denote unique subclusters and individuals

2.2 |. Statistical model

We consider a GLMM to represent the average secular trend, intervention effect, as well as the three-level structure within each period. Let Y_ijkl be the outcome of interest for individual l = 1, … , N_ijk nested in subcluster k = 1, … , K_ij nested in cluster i = 1, … , I during period j = 1, … , T. For generality, we assume design (A), where a closed-cohort of subjects in the same set of subclusters are measured in the study during each period. Designs (B) and (C) will be cast as two special cases. For design (A), the conditional mean model for ${\mu }_{\mathit{\text{ijkl}}}=\mathbb{E}\left(Y_{\mathit{\text{ijkl}}}\mid b_i,c_{\mathit{\text{ik}}},s_{\mathit{\text{ij}}},{\pi }_{\mathit{\text{ijk}}},{\gamma }_{\mathit{\text{ikl}}}\right)$ is given by

$$g\left({\mu }_{\mathit{\text{ijkl}}}\right)={\beta }_j+\delta X_{\mathit{\text{ij}}}+b_i+c_{\mathit{\text{ik}}}+s_{\mathit{\text{ij}}}+{\pi }_{\mathit{\text{ij}}k}+{\gamma }_{\mathit{\text{ik}}l},$$ (1)

where g is a link function, β_j represents the categorical secular trend, X_ij is the intervention status for cluster i at period j (equal to 1 if exposed under intervention and 0 otherwise), and δ is the intervention effect of interest on the link function scale. We also write θ = (β₁, … , β_T, δ)^⊤. Model (1) includes five random effects to reflect the multilevel structure of the data: $b_i~\mathcal{N}\left(0,{\sigma }_b^2\right)$ is the random cluster effect, $c_{\mathit{\text{ik}}}~\mathcal{N}\left(0,{\sigma }_c^2\right)$ is the random subcluster effect, $s_{\mathit{\text{ij}}}~\mathcal{N}\left(0,{\sigma }_S^2\right)$ is the random cluster-by-period interaction, and ${\pi }_{\mathit{\text{ij}}k}~\mathcal{N}\left(0,{\sigma }_{\pi }^2\right)$ is the random subcluster-by-period interaction. Furthermore, since design (A) involves a closed-cohort of subjects, ${\gamma }_{\mathit{\text{ik}}l}~\mathcal{N}\left(0,{\sigma }_{\gamma }^2\right)$ is the random subject-level effect arising from the repeated outcome measurements for each same subject. In particular, the random interactions, s_ij and π_ijk, can represent variations within each cluster and subcluster due to time-varying characteristics of the cluster and each subcluster. The inclusion of these random interactions further allows the within-period ICCs to differ from the between-period ICCs at each level of clustering, which is considered critical for accurate power calculation even in SW-CRTs without subclusters (Taljaard et al., 2016). Following convention in modeling for SW-CRTs (Li et al., 2021), we assume all random effects are mutually independent and Y_ijkl is a random realization from a parametric distribution with mean μ_ijkl and higher order moments as potential functions of μ_ijkl. Model (1) includes several existing models for SW-CRTs as special cases. For example, when ${\sigma }_s^2={\sigma }_{\pi }^2={\sigma }_{\gamma }^2=0$, model (1) coincides with the model in Hemming et al. (2015) for cross-sectional SW-CRTs; when ${\sigma }_s^2={\sigma }_{\pi }^2=0$, model (1) becomes the model in Teerenstra et al. (2019) without cluster- or subcluster-by-time interactions; when ${\sigma }_c^2={\sigma }_{\pi }^2=0$, model (1) reduces to the model in Hooper et al. (2016) for closed-cohort SW-CRTs without subclusters. Finally, models for design (B) or (C) can be obtained by setting ${\sigma }_{\gamma }^2=0$ or ${\sigma }_{\gamma }^2={\sigma }_c^2=0$ in model (1), due to the absence of repeated assessments for the same subjects or the same subclusters.

2.3 |. Generic sample size requirement

In the design phase, the power to detect an effect size δ ≠ 0 with a two-sided α-level Wald test is approximately (Harrison and Brady, 2004)

$$\text{power}\approx 1-{\Phi }_t\left(t_{\alpha /2,\text{DoF}};\text{DoF},\left|\delta \right|/\sqrt{\text{var}(\widehat{\delta })}\right),$$ (2)

where t_α/2,DoF is the upper α/2th quantile of the central t-distribution with specified degrees of freedom (DoF) and Φ_t(t; DoF, Λ) is the cumulative t-distribution function with DoF and noncentrality parameter Λ. The variance of the intervention effect, $\text{var}(\widehat{\delta })$, is an implicit function of the number of clusters (I) and other design parameters. While power expression (2) is asymptotically equivalent to its counterpart with a standard normal distribution as the DoF approach infinity, we consider the t-distribution with DoF = I − 2 since it has been found to maintain a valid empirical type I error rate with a limited number of clusters in SW-CRTs (Ford and Westgate, 2020; Li et al., 2021). By Equation (2), the sample size requirement for the multilevel SW-CRT requires us to characterize an expression of $\text{var}(\widehat{\delta })$ at the design phase. To do so, we first assume equal cluster and subcluster sizes such that K_ij = K and N_ijk = N. We relax this assumption in Section 3.3.

3 |. VARIANCE OF THE INTERVENTION EFFECT ESTIMATOR

3.1 |. Gaussian outcomes

With a Gaussian outcome, we consider g in model (1) to be the identity function, and assume Y_ijkl = μ_ijkl + ϵ_ijkl, where ${ϵ}_{\mathit{\text{ijkl}}}~\mathcal{N}\left(0,{\sigma }_{ϵ}^2\right)$ is an independent residual error. In this linear mixed model, we define ${\sigma }^2={\sigma }_b^2+{\sigma }_c^2+{\sigma }_s^2+{\sigma }_{\pi }^2+{\sigma }_{\gamma }^2+{\sigma }_{ϵ}^2$ as the total variance. Under design (A), this linear mixed model induces five different ICCs: (i) the within-period within-subcluster ICC, α₀; (ii) the between-period within-subcluster ICC, α₁; (iii) the within-period between-subcluster ICC, ρ₀; (iv) the between-period between-subcluster ICC, ρ₁; and (v) the within-subject autocorrelation, α₂. We explicitly define the ICCs as functions of variance components under each design variant in Table 1.

TABLE 1.

Definition of ICCs: within-period within-subcluster (α₀), between-period within-subcluster (α₁), within-subject auto-correlation (α₂), within-period between-subcluster (ρ₀), and between-period between-subcluster (ρ₁) under each design variant: (A) Closed-cohort design at both the subcluster and subject levels (total variance ${\sigma }_A^2={\sigma }_b^2+{\sigma }_c^2+{\sigma }_s^2+{\sigma }_{\pi }^2+{\sigma }_{\gamma }^2+{\sigma }_{ϵ}^2$), (B) Closed-cohort design on the subcluster level but a cross-sectional design at the subject level (total variance ${\sigma }_B^2={\sigma }_b^2+{\sigma }_c^2+{\sigma }_S^2+{\sigma }_{\pi }^2+{\sigma }_{ϵ}^2$), and (C) Cross-sectional design at both the subcluster and subject level (total variance ${\sigma }_C^2={\sigma }_b^2+{\sigma }_s^2+{\sigma }_{\pi }^2+{\sigma }_{ϵ}^2$)

ICC	Definition	Design (A)	Design (B)	Design (C)
α 0	corr (Yijkl, Yijkl′)	$\left({\sigma }_b^2+{\sigma }_c^2+{\sigma }_S^2+{\sigma }_{\pi }^2\right)/{\sigma }_A^2$	$\left({\sigma }_b^2+{\sigma }_c^2+{\sigma }_s^2+{\sigma }_{\pi }^2\right)/{\sigma }_B^2$	$\left({\sigma }_b^2+{\sigma }_s^2+{\sigma }_{\pi }^2\right)/{\sigma }_C^2$
α 1	corr (Yijkl, Yij′kl′)	$\left({\sigma }_b^2+{\sigma }_c^2\right)/{\sigma }_A^2$	$\left({\sigma }_b^2+{\sigma }_c^2\right)/{\sigma }_B^2$	ρ 1
α 2	corr (Yijkl, Yij′kl)	$\left({\sigma }_b^2+{\sigma }_c^2+{\sigma }_{\gamma }^2\right)/{\sigma }_A^2$	α 1	ρ 1
ρ 0	corr (Yijkl, Yijk′l′)	$\left({\sigma }_b^2+{\sigma }_s^2\right)/{\sigma }_A^2$	$\left({\sigma }_b^2+{\sigma }_S^2\right)/{\sigma }_B^2$	$\left({\sigma }_b^2+{\sigma }_S^2\right)/{\sigma }_C^2$
ρ 1	corr (Yijkl, Yij′k′l′)	${\sigma }_b^2/{\sigma }_A^2$	${\sigma }_b^2/{\sigma }_B^2$	${\sigma }_b^2/{\sigma }_C^2$

As the variance components are nonnegative, we implicitly have α₀ ≥ α₁ ≥ ρ₁, α₀ ≥ ρ₀ ≥ ρ₁, and α₂ ≥ α₁ ≥ ρ₁ without further restrictions. To aid in the interpretation of ICCs, an investigator could also parameterize the between-period ICCs based on the within-period ICCs by assuming a particular cluster autocorrelation coefficient (CAC), defined as the ratio of between-period to within-period ICCs (Hooper et al., 2016; Martin et al., 2016). Because ICCs are conventionally used in designing CRTs and intuitive to understand, we will characterize the variance of the intervention effect with these five ICC parameters and obtain the variances for design (B) or (C) by setting α₂ = α₁, or α₂ = α₁ = ρ₁. In addition, the variance components or ICCs should ensure a positive definite correlation structure for all outcomes within each cluster. Specifically, if we define ${\mathit{\text{Y}}}_i={\left({\mathit{\text{Y}}}_{i1}^{\top },\dots .{\mathit{\text{Y}}}_{\mathit{\text{iT}}}^{\top }\right)}^{\top }$, where ${\mathit{\text{Y}}}_{\mathit{\text{ij}}}={\left({\mathit{\text{Y}}}_{\mathit{\text{ij}}1}^{\top },\dots ,{\mathit{\text{Y}}}_{\mathit{\text{ij}}K}^{\top }\right)}^{\top }$, and ${\mathit{\text{Y}}}_{\mathit{\text{ij}}k}={\left(Y_{\mathit{\text{ijk}}1},\dots ,Y_{\mathit{\text{ijkN}}}\right)}^{\top }$, then the induced correlation structure, R_i = corr(Y_i), follows an extended block exchangeable structure and can be written as a linear combination of six basis matrices,

$$\begin{gathered} {\mathit{\text{R}}}_i=\left(1-{\alpha }_0-{\alpha }_2+{\alpha }_1\right){\mathit{\text{I}}}_{\mathit{\text{TKN}}}+\left({\alpha }_0-{\rho }_0-{\alpha }_1+{\rho }_1\right){\mathit{\text{I}}}_{\mathit{\text{TK}}} \\ \otimes {\mathit{\text{J}}}_N+\left({\rho }_0-{\rho }_1\right){\mathit{\text{I}}}_T\otimes {\mathit{\text{J}}}_{\mathit{\text{KN}}} \\ +\left({\alpha }_2-{\alpha }_1\right){\mathit{\text{J}}}_T\otimes {\mathit{\text{I}}}_{\mathit{\text{KN}}}+\left({\alpha }_1-{\rho }_1\right){\mathit{\text{J}}}_T \\ \otimes {\mathit{\text{I}}}_K\otimes {\mathit{\text{J}}}_N+{\rho }_1{\mathit{\text{J}}}_{\mathit{\text{TKN}}}, \end{gathered}$$ (3)

where I_u is a u × u identity matrix and ${\mathit{\text{J}}}_u=1_u{1}_u^{\top }$ is a u × u matrix of ones. Evidently, the diagonal and off-diagonal KN × KN blocks of R_i are block exchangeable given by ${\mathit{\text{I}}}_K\otimes \left\{\left(1-{\alpha }_0\right){\mathit{\text{I}}}_N+\left({\alpha }_0-{\rho }_0\right){\mathit{\text{J}}}_N\right\}+{\rho }_0{\mathit{\text{J}}}_{\mathit{\text{KN}}}$ and ${\mathit{\text{I}}}_K\otimes \left\{\left({\alpha }_2-{\alpha }_1\right){\mathit{\text{I}}}_N+\left({\alpha }_1-{\rho }_1\right){\mathit{\text{J}}}_N\right\}+{\rho }_1{\mathit{\text{J}}}_{\mathit{\text{KN}}}$, respectively, and, therefore, the structure (3) resembles the block exchangeable structure studied in Li et al. (2018). For deriving the variance of the intervention effect, we first provide the two key intermediate results on the induced correlation structure.

Lemma 1. The induced extended block exchangeable correlation matrix has at most six unique eigenvalues, which can be expressed as linear functions of the five ICC parameters:

$$\begin{gathered} {\lambda }_1=1-{\alpha }_0-{\alpha }_2+{\alpha }_1 \\ {\lambda }_2=1-{\alpha }_0-{\alpha }_2+{\alpha }_1+N\left({\alpha }_0-{\alpha }_1-{\rho }_0+{\rho }_1\right) \\ {\lambda }_3=1-{\alpha }_0-{\alpha }_2+{\alpha }_1+N\left\{{\alpha }_0-{\alpha }_1+(K-1)\left({\rho }_0-{\rho }_1\right)\right\} \\ {\lambda }_4=1-{\alpha }_0+(T-1)\left({\alpha }_2-{\alpha }_1\right) \\ {\lambda }_5=1-{\alpha }_0+(T-1)\left({\alpha }_2-{\alpha }_1\right) \\ +N\left\{{\alpha }_0-{\rho }_0+(T-1)\left({\alpha }_1-{\rho }_1\right)\right\} \\ {\lambda }_6=1-{\alpha }_0+(T-1)\left({\alpha }_2-{\alpha }_1\right) \\ +N\left[{\alpha }_0+(T-1){\alpha }_1+(K-1)\left\{{\rho }_0+(T-1){\rho }_1\right\}\right] \end{gathered}$$ (4)

with algebraic multiplicities (T − 1)K(N − 1), (T − 1)(K − 1), T − 1, K(N − 1), K − 1, and 1, respectively. The set of ICC parameters {α₀, α₁, α₂, ρ₀, ρ₁} for which R_i is positive definite corresponds to the convex open subset characterized by min{λ₁, λ₂, λ₃, λ₄, λ₅, λ₆} > 0.

Lemma 2.The extended block exchangeable correlation matrix has a closed-form inverse, which shares the same set of basis matrices withR_i, with coefficients determined by the set of eigenvalues. The inverse is represented as

$$\begin{gathered} {\mathit{\text{R}}}_i^{-1}=\frac{1}{{\lambda }_1}{\mathit{\text{I}}}_{\mathit{\text{TKN}}}-\frac{{\lambda }_2-{\lambda }_1}{N{\lambda }_1{\lambda }_2}{\mathit{\text{I}}}_{\mathit{\text{TK}}}\otimes {\mathit{\text{J}}}_N+\frac{{\lambda }_2-{\lambda }_3}{\mathit{\text{KN}}{\lambda }_2{\lambda }_3}{\mathit{\text{I}}}_T\otimes {\mathit{\text{J}}}_{\mathit{\text{KN}}} \\ +\frac{1}{T}\left(\frac{1}{{\lambda }_4}-\frac{1}{{\lambda }_1}\right){\mathit{\text{J}}}_T\otimes {\mathit{\text{I}}}_{\mathit{\text{KN}}} \\ +\frac{1}{T}\left(\frac{{\lambda }_2-{\lambda }_1}{N{\lambda }_1{\lambda }_2}-\frac{{\lambda }_5-{\lambda }_4}{N{\lambda }_4{\lambda }_5}\right){\mathit{\text{J}}}_T\otimes {\mathit{\text{I}}}_K\otimes {\mathit{\text{J}}}_N \\ +\frac{1}{\mathit{\text{TK}}}\left(\frac{{\lambda }_5-{\lambda }_6}{N{\lambda }_5{\lambda }_6}-\frac{{\lambda }_2-{\lambda }_3}{N{\lambda }_2{\lambda }_3}\right){\mathit{\text{J}}}_{\mathit{\text{TKN}}}. \end{gathered}$$

Lemmas 1 and 2 derive the eigenvalues as well as an explicit inverse of the extended block exchangeable correlation structure (derivation details and eigenvalue expressions under each design variant are provided in Web Appendix A and Web Table 1). By parameterizing ${\mathit{\text{R}}}_i^{-1}$ as a function of the unique eigenvalues, the cumbersome expressions on individual ICCs are avoided in deriving an explicit variance expression of the intervention effect.

Assuming the variance components are known, the feasible generalized least squares estimator for θ is given by $\widehat{\mathit{\theta }}={\left({\mathbf{\sum }}_{i=1}^I{\mathit{\text{Z}}}_i^{\top }{\mathit{\text{R}}}_i^{-1}{\mathit{\text{Z}}}_i\right)}^{-1}\left({\mathbf{\sum }}_{i=1}^I{\mathit{\text{Z}}}_i^{\top }{\mathit{\text{R}}}_i^{-1}{\mathit{\text{Y}}}_i\right)$, where Z_i = (I_T, X_i) ⊗ 1_KN is the design matrix for fixed effects and X_i = (X_i1, … , X_iT)^⊤ is the vector of cluster-level intervention indicators. As the number of clusters becomes large, $\widehat{\mathit{\theta }}$ follows a multivariate normal distribution with mean θ and covariance matrix ${\sigma }^2{\left({\mathbf{\sum }}_{i=1}^I{\mathit{\text{Z}}}_i^{\top }{\mathit{\text{R}}}_i^{-1}{\mathit{\text{Z}}}_i\right)}^{-1}$, whose (T + 1, T + 1)th element corresponds to the variance of the intervention effect estimator. Based on Lemma 2, we show in Web Appendix A that a closed-form expression of $\text{var}(\widehat{\delta })$ exists, which reveals the impact of various ICC parameters on sample size and power. We summarize the results in Theorem 1.

Theorem 1. Assuming known variance components, the closed-form variance of the intervention effect estimator based on a linear mixed model with a Gaussian outcome is

$$\mathit{\text{var}}(\widehat{\delta })=\frac{{\sigma }^2}{\mathit{\text{IKNtr}}(\Omega )}\times \frac{T{\lambda }_6{\lambda }_3}{T{\lambda }_6-\left\{1+(T-1){\tau }_X\right\}\left({\lambda }_6-{\lambda }_3\right)},$$ (5)

where

$$\Omega =I^{-1}\mathbf{\sum }_{i=1}^I{\mathit{\text{X}}}_i{\mathit{\text{X}}}_i^{\top }-\left(I^{-1}\mathbf{\sum }_{i=1}^I{\mathit{\text{X}}}_i\right)\left(I^{-1}\mathbf{\sum }_{i=1}^I{\mathit{\text{X}}}_i^{\top }\right)$$

is the covariance matrix of the intervention vector under a specific design and ${\tau }_X={\{(T-1)\mathit{\text{tr}}(\Omega )\}}^{-1}\left\{1_T^{\top }\Omega 1_T-\mathit{\text{tr}}(\Omega )\right\}\in [-1,1]$ is the generalized ICC of the intervention, which is the ratio of average covariance over the average variance and measures the similarity between the intervention status for each cluster in different periods (Kistner and Muller, 2004). With all other design parameters fixed, larger values of the within-period ICCs, {α₀, ρ₀}, are always associated with larger required sample size, whereas larger values of the between-period ICCs, {α₁, ρ₁, α₂}, are associated with smaller required sample size when ${\tau }_X<\left({\lambda }_6^2-{\lambda }_3^2\right)/\left\{{\lambda }_6^2+(T-1){\lambda }_3^2\right\}$.

Theorem 1 reveals that the variance of the intervention effect in a linear mixed model is free of the secular trend, as long as it is adjusted for in the model. The variance (5) also depends on the five ICCs only through two eigenvalues of the extended block exchangeable correlation matrix, λ₃ and λ₆. Our results also confirm the different roles of the within-period ICCs and the between-period ICCs. Specifically in the design phase, assuming larger values of α₀ and ρ₀ will only lead to a conservative sample size estimate. Likewise, assuming smaller values of between-period ICCs or even ignoring them by considering α₂ = α₁ = ρ₁ = 0 will lead to a conservative sample size estimate if the constraint on τ_X holds. These directional results can guide decisions on design parameters to avoid an underpowered trial in the absence of accurate ICC estimates for an SW-CRT with subclusters. Finally, while we assume design (A), variance expressions for design (B) or (C) can be easily obtained by enforcing α₂ = α₁, or α₂ = α₁ = ρ₁ in computing the two eigenvalues.

As expected from the generality of model (1), our variance expression (5) includes a number of variances previously derived as special cases. First, we observe that the variance (5) can be alternatively represented by

$$\text{var}(\widehat{\delta })=\frac{\left({\sigma }^2/\mathit{\text{KN}}\right)\mathit{\text{IT}}{\lambda }_6{\lambda }_3}{\left(U^2+\mathit{\text{ITU}}-\mathit{\text{TW}}-\mathit{\text{IV}}\right){\lambda }_6-\left(U^2-\mathit{\text{IV}}\right){\lambda }_3},$$ (6)

where

$$U=\mathbf{\sum }_{i=1}^I\mathbf{\sum }_{j=1}^T{X}_{\mathit{\text{ij}}},V=\mathbf{\sum }_{i=1}^I{\left(\mathbf{\sum }_{j=1}^T{X}_{\mathit{\text{ij}}}\right)}^2,$$

and

$$W=\mathbf{\sum }_{j=1}^T{\left(\mathbf{\sum }_{i=1}^I{X}_{\mathit{\text{ij}}}\right)}^2$$

are typical design constants that only depend on the sequence of treatment indicators for each cluster. The connection between the two variance expressions is made clear through the observance that $1_T^{\top }\Omega 1_T=I^{-2}\left(\mathit{\text{IV}}-U^2\right)$ and t(Ω) = I⁻²(IU − W). Using this equivalent variance expression (6), we see that in the absence of subclusters, the variance derived in Li et al. (2018) under a closed-cohort SW-CRT is obtained by setting ρ₀ = α₀ and ρ₁ = α₁; the variance of the Hooper et al. (2016) linear mixed model under a cross-sectional SW-CRT can be obtained by additionally requiring α₂ = α₁; whereas the basic Hussey and Hughes (2007) linear mixed model is obtained by equating all five ICCs. In the presence of subclusters, our variance expression also includes that derived in Teerenstra et al. (2019) as a special case when we assume ρ₁ = ρ₀ and α₁ = α₀. However, we caution against this simplification assumption, because based on (6), we observe that lim_N→∞(λ₃/N) = (α₀ − α₁) + (K − 1)(ρ₀ − ρ₁), and lim_N→∞(λ₆/N) = α₀ + (T − 1)α₁ + (K − 1){ρ₀ + (T − 1)ρ₁} = κ(α₀, α₁, ρ₀, ρ₁), which leads to a limiting variance

$$\underset{N\to \infty }{\text{lim}}\text{var}(\widehat{\delta })=\frac{\left({\sigma }^2/K\right)\left\{\left({\alpha }_0-{\alpha }_1\right)+(K-1)\left({\rho }_0-{\rho }_1\right)\right\}I\kappa \left({\alpha }_0,{\alpha }_1,{\rho }_0,{\rho }_1\right)}{(\mathit{\text{IU}}-W)\kappa \left({\alpha }_0,{\alpha }_1,{\rho }_0,{\rho }_1\right)+\left(U^2-\mathit{\text{IV}}\right)\left\{{\alpha }_1+(K-1){\rho }_1\right\}}.$$

Therefore, assuming the between-period ICCs are equal to the within-period ICCs, the limiting variance approaches zero and the required number of clusters approaches one as the subcluster size increases indefinitely, similar to the discussion in Taljaard et al. (2016) without subclusters. From this perspective, it is reasonable to differentiate the between-period ICCs from the within-period ICCs and avoid the risks associated with too few clusters in the design phase. Furthermore, based on the proposed analytical variance (6), we show in Web Appendix B that the most efficient SW-CRT with subclusters allocates more clusters to the intervention during the second and last period.

Finally, while we have thus far focused on stepped wedge designs with a staggered allocation of intervention to clusters, the derivations of Theorem 1 do not involve restrictions on X_i, and therefore expression (5) applies more generally to any multiperiod CRT, including the longitudinal parallel-arm and repeated crossover designs. Clearly, variance (5) reveals that higher efficiency is achieved with a larger total variance of the intervention status, tr(Ω), and a smaller generalized ICC of the intervention, τ_X, both of which a specific design will implicitly characterize. For example, with T = 5 periods and I as a multiple of (T − 1), a standard stepped wedge design corresponds to t(Ω) = 0.625 and τ_X = 0.25, a parallel longitudinal design corresponds to tr(Ω) = 1.25 and τ_X = 1, whereas a repeated crossover design engenders tr(Ω) = 1.25 and τ_X = −0.2. In Web Table 2, we show that a repeated crossover design and a parallel longitudinal design have the same values of t(Ω), which is generally larger than that under a standard stepped wedge design. Furthermore, the generalized ICC of the intervention indicator is maximal under a longitudinal parallel-arm design, whereas τ_X ∈ (0, 1) in a standard stepped wedge design. However, the generalized ICC, τ_X, is often negative under a repeated crossover design. Such insights could facilitate the comparison of relative efficiency for alternative designs with subclusters.

3.2 |. Non-Gaussian exponential family outcomes

When the outcome is binary or count, Theorem 1 is not directly applicable because the residual variance function of the outcome is no longer a constant. Specifically, with a link function g, we can rewrite the conditional mean of the outcome Y_ijkl from (1) as

$${\mu }_{\mathit{\text{ijkl}}}=g^{-1}\left({\eta }_{\mathit{\text{ijkl}}}\right)=g^{-1}\left({\beta }_j+\delta X_{\mathit{\text{ij}}}+b_i+c_{\mathit{\text{ik}}}+s_{\mathit{\text{ij}}}+{\pi }_{\mathit{\text{ij}}k}+{\gamma }_{\mathit{\text{ik}}l}\right),$$ (7)

where the fixed and random effects are defined in Section 2.2. We further define the conditional variance of the outcome as ϕζ(μ_ijkl), where ϕ is a common dispersion. Without loss of generality, we assume ϕ = 1 but the following procedure applies to arbitrary ϕ > 0. For example, the variance function of a binary outcome is parameterized as ζ(μ_ijkl) = μ_ijkl(1 − μ_ijkl). To approximate the large-sample variance of the maximum likelihood estimator for $\widehat{\delta }$, we linearize model (7) by a first-order Taylor expansion about the estimated fixed- and random-effects (Breslow and Clayton, 1993; Amatya and Bhaumik, 2018) such that

$$\begin{gathered} {\mathit{\text{Y}}}_{\mathit{\text{ij}}}={\widehat{\mathit{\mu }}}_{\mathit{\text{ij}}}+{\widehat{\Delta }}_{\mathit{\text{ij}}}{\mathit{\text{Z}}}_{\mathit{\text{ij}}}(\mathit{\theta }-\widehat{\mathit{\theta }})+{\widehat{\Delta }}_{\mathit{\text{ij}}}{1}_{\mathit{\text{KN}}}\left(b_i-{\widehat{b}}_i\right) \\ +{\widehat{\Delta }}_{\mathit{\text{ij}}}\left({\mathit{\text{I}}}_K\otimes 1_N\right)\left({\mathit{\text{c}}}_{\mathit{\text{ij}}}-{\widehat{\mathit{\text{c}}}}_{\mathit{\text{ij}}}\right)+{\widehat{\Delta }}_{\mathit{\text{ij}}}{1}_{\mathit{\text{KN}}}\left(s_{\mathit{\text{ij}}}-{\widehat{s}}_{\mathit{\text{ij}}}\right) \\ +{\widehat{\Delta }}_{\mathit{\text{ij}}}\left({\mathit{\text{I}}}_K\otimes 1_N\right)\left({\mathit{\pi }}_{\mathit{\text{ij}}}-{\widehat{\mathit{\pi }}}_{\mathit{\text{ij}}}\right)+{\widehat{\Delta }}_{\mathit{\text{ij}}}\left({\mathit{\gamma }}_{\mathit{\text{ij}}}-{\widehat{\mathit{\gamma }}}_{\mathit{\text{ij}}}\right)+{\mathit{ϵ}}_{\mathit{\text{ij}}}, \end{gathered}$$ (8)

where ${\mathbf{\Delta }}_{\mathit{\text{ij}}}=\text{diag}\left({\Delta }_{\mathit{\text{ij}}11},\dots ,{\Delta }_{\mathit{\text{ijKN}}}\right)={\left\{\partial g^{-1}\left({\mathit{\eta }}_{\mathit{\text{ij}}}\right)/\partial {\mathit{\eta }}_{\mathit{\text{ij}}}^{\top }\right\}}^{-1}$ is a diagonal matrix of derivatives, η_ij = (η_ij11, … , η_ijKN)^⊤, μ_ij = (μ_ij11, … , μ_ijKN)^⊤, Z_ij = (e_j, X_ij) ⊗ 1_KN (e_j is the jth row of I_T), c_ij = (c_i1, … , c_iK)^⊤, π_ij = (π_ij1, … , π_ijK)^⊤, γ_ij = (γ_i11, … , γ_iKN)^⊤, ϵ_ij = (ϵ_ij11, … , ϵ_ijKN)^⊤, and var(ϵ_ijkl) = ζ(μ_ijkl). Therefore, if we define the vector of pseudo-outcomes as ${\mathit{\text{Y}}}_{\mathit{\text{ij}}}^{*}={\widehat{\mathbf{\Delta }}}_{\mathit{\text{ij}}}^{-1}\left({\mathit{\text{Y}}}_{\mathit{\text{ij}}}-{\widehat{\mathit{\mu }}}_{\mathit{\text{ij}}}\right)+{\widehat{\mathit{\eta }}}_{\mathit{\text{ij}}}$ and rearrange the terms in (8), we obtain an approximate linear mixed model with ${\mathit{\text{Y}}}_{\mathit{\text{ij}}}^{*}={\mathit{\eta }}_{\mathit{\text{ij}}}+{\mathit{ϵ}}_{\mathit{\text{ij}}}^{*}$, with a modified random residual error ${\mathit{ϵ}}_{\mathit{\text{ij}}}^{*}={\widehat{\mathbf{\Delta }}}_{\mathit{\text{ij}}}^{-1}{\mathit{ϵ}}_{\mathit{\text{ij}}}$. Define the collection of all pseudo-outcomes in cluster i as ${\mathit{\text{Y}}}_i^{*}={\left({\mathit{\text{Y}}}_{i1}^{*\top },\dots ,{\mathit{\text{Y}}}_{\mathit{\text{iT}}}^{*\top }\right)}^{\top }$, we show in Web Appendix C that

$$\begin{gathered} {\mathit{\text{V}}}_i=\text{cov}\left({\mathit{\text{Y}}}_i^{*}\right)\approx \mathbb{E}\left\{{\Delta }_i^{-1}\zeta \left({\mathit{\mu }}_i\right){\Delta }_i^{-1}\right\} \\ +{\sigma }_{\pi }^2\left({\mathit{\text{I}}}_{\mathit{\text{TK}}}\otimes {\mathit{\text{J}}}_N\right)+{\sigma }_S^2\left({\mathit{\text{I}}}_T\otimes {\mathit{\text{J}}}_{\mathit{\text{KN}}}\right)+{\sigma }_{\gamma }^2\left({\mathit{\text{J}}}_T\otimes {\mathit{\text{I}}}_{\mathit{\text{KN}}}\right) \\ +{\sigma }_c^2\left({\mathit{\text{J}}}_T\otimes {\mathit{\text{I}}}_K\otimes {\mathit{\text{J}}}_N\right)+{\sigma }_b^2{\mathit{\text{J}}}_{\mathit{\text{TKN}}}, \end{gathered}$$ (9)

with ${\Delta }_i={\oplus }_{j=1}^T{\Delta }_{\mathit{\text{ij}}}$ where “⊕” is a block diagonal operator with nonzero matrices along the diagonal and zero values elsewhere, and the expectation is taken over the distribution of all the random effects. In general, $\mathbb{E}\left\{{\mathbf{\Delta }}_i^{-1}\zeta \left({\mathit{\mu }}_i\right){\mathbf{\Delta }}_i^{-1}\right\}$ can be computed via numerical integration and depends on the conditional mean of outcomes through the secular trend and intervention status, thus V_i will be cluster specific. The approximate covariance matrix of the estimator for fixed-effects parameters based on the pseudo-outcomes is then ${\left({\sum }_{i=1}^I{\mathit{\text{Z}}}_i^{\top }{\mathit{\text{V}}}_i^{-1}{\mathit{\text{Z}}}_i\right)}^{-1}$, whose (T + 1, T + 1)th element is

$$\begin{gathered} \text{var}(\widehat{\delta })={\left[\sum _{i=1}^I\left({\mathit{\text{X}}}_i^{\top }\otimes 1_{\mathit{\text{KN}}}^{\top }\right)V_i^{-1}\left({\mathit{\text{X}}}_i\otimes 1_{\mathit{\text{KN}}}\right)-\left\{\sum _{i=1}^I\left({\mathit{\text{X}}}_i^{\top }\otimes 1_{\mathit{\text{KN}}}^{\top }\right)V_i^{-1}\left({\mathit{\text{I}}}_T\otimes 1_{\mathit{\text{KN}}}\right)\right\} \\ \times {\left\{\sum _{i=1}^I\left({\mathit{\text{I}}}_T^{\top }\otimes 1_{\mathit{\text{KN}}}^{\top }\right)V_i^{-1}\left({\mathit{\text{I}}}_T\otimes 1_{\mathit{\text{KN}}}\right)\right\}}^{-1} \\ \times \left\{\left({\mathit{\text{I}}}_T^{\top }\otimes 1_{\mathit{\text{KN}}}^{\top }\right)\sum _{i=1}^I{V}_i^{-1}\left({\mathit{\text{X}}}_i\otimes 1_{\mathit{\text{KN}}}\right)\right\}\right]}^{-1}. \end{gathered}$$

In the design stage, computation of the above variance requires us to invert the TKN × TKN variance matrix, V_i, for each cluster, which could require substantial computational time as the subcluster size or the number of subclusters become large. However, because the fixed effects in (7) only depends on each cluster period, we provide an equivalent but computationally more efficient variance expression in the following lemma.

Lemma 3. The variance of the intervention effect estimator in the GLMM (7) is equivalently written as

$$\mathit{\text{var}}(\widehat{\delta })={\left\{\mathbf{\sum }_{i=1}^I{\mathit{\text{X}}}_i^{\top }{\widetilde{\mathit{\text{V}}}}_i^{-1}{\mathit{\text{X}}}_i-\left(\mathbf{\sum }_{i=1}^I{\mathit{\text{X}}}_i^{\top }{\widetilde{\mathit{\text{V}}}}_i^{-1}\right)\times {\left(\mathbf{\sum }_{i=1}^I{\widetilde{\mathit{\text{V}}}}_i^{-1}\right)}^{-1}\left(\mathbf{\sum }_{i=1}^I{\widetilde{\mathit{\text{V}}}}_i^{-1}{\mathit{\text{X}}}_i\right)\right\}}^{-1},$$ (10)

where ${\widetilde{\mathit{\text{V}}}}_i={(\mathit{\text{KN}})}^{-1}{\mathit{\text{E}}}_i+\left(K^{-1}{\sigma }_{\pi }^2+{\sigma }_s^2\right){\mathit{\text{I}}}_T+\left\{{\sigma }_b^2+K^{-1}{\sigma }_c^2+{(\mathit{\text{KN}})}^{-1}{\sigma }_{\gamma }^2\right\}{\mathit{\text{J}}}_T$ is the T × T matrix characterizing the covariance of the cluster period means of the pseudo-outcomes ${\overline{\mathit{\text{Y}}}}_i^{*}={(\mathit{\text{KN}})}^{-1}\left({\mathit{\text{I}}}_T\otimes 1_{\mathit{\text{KN}}}^{\top }\right){\mathit{\text{Y}}}_i^{*}$ , and ${\mathit{\text{E}}}_i=\text{diag}\left[\mathbb{E}\left\{{\Delta }_{i111}^{-1}\zeta \left({\mu }_{i111}\right){\Delta }_{i111}^{-1}\right\},\dots ,\mathbb{E}\left\{{\Delta }_{\mathit{iT}11}^{-1}\zeta \left({\mu }_{\mathit{iT}11}\right){\Delta }_{\mathit{iT}11}^{-1}\right\}\right]$.

By providing an equivalent variance expression, Lemma 3 indicates that one only needs to invert a set of T × T matrices to obtain the variance for power calculation for general exponential family outcomes with a certain mean-variance structure and alleviates the computational burden associated with inverting a series of TKN × TKN matrices. While Lemma 3 is easy to verify when V_i has a closed-form inverse (as when the variance function ζ(μ_ijkl) ∝ 1), it is not trivial for general variance functions and requires us to exploit the block structure of $\mathbb{E}\left\{{\mathbf{\Delta }}_i^{-1}\zeta \left({\mathit{\mu }}_i\right){\mathbf{\Delta }}_i^{-1}\right\}$ under a stepped wedge design; the detailed proof is provided in Web Appendix C. Finally, Lemma 3 implies that $\text{var}(\widehat{\delta })$ can be equivalently considered as that obtained from a linear mixed model for the cluster period mean pseudo-outcomes ${\overline{\mathit{\text{Y}}}}_i^{*}$ and is therefore an extension of the results in Li et al. (2021) to more complex correlation structures, under equal subcluster sizes.

From variance expression (10), it is critical to compute the nonzero diagonal elements of E_i, where the expectation involves integration over all the random effects. While numerical or Monte Carlo integration can be used as a general solution, the computation of these terms can be considerably simplified under canonical link functions. For example, with a binary outcome and a canonical logit link, we can use the property of the Gaussian moment generating function to obtain the jth diagonal element of E_i as

$$\begin{gathered} \mathbb{E}\left\{{\Delta }_{\mathit{\text{ij}}11}^{-1}\zeta \left({\mu }_{\mathit{\text{ij}}11}\right){\Delta }_{\mathit{\text{ij}}11}^{-1}\right\} \\ =2+2\text{ exp}\left(\frac{{\sigma }_b^2+{\sigma }_c^2+{\sigma }_s^2+{\sigma }_{\pi }^2+{\sigma }_{\gamma }^2}{2}\right) \\ \times \text{cosh}\left({\beta }_j+X_{\mathit{\text{ij}}}\delta \right), \end{gathered}$$

where cosh(t) = (e^t + e^−t)/2 is the hyperbolic cosine function. In cases when the ICCs are more intuitive parameters than variance components to consider in the design phase, we could use the latent response formulation and define the total variance as ${\sigma }^2={\sigma }_b^2+{\sigma }_c^2+{\sigma }_s^2+{\sigma }_{\pi }^2+{\sigma }_{\gamma }^2+{\pi }^2/3$, where π²/3 is the variance of the standard logistic distribution (Eldridge et al., 2009). This formulation allows us to reparameterize $\text{var}(\widehat{\delta })$ with σ² and the five ICCs (Table 1). Specifically, using Lemma 3 the variance matrix under a binary outcome with a logit link can be represented by

$${\widetilde{\mathit{\text{V}}}}_i=\frac{1}{\mathit{\text{KN}}}{\mathit{\text{E}}}_i+\frac{\left({\lambda }_3-{\lambda }_1\right){\sigma }^2}{\mathit{\text{KN}}}{\mathit{\text{I}}}_T+\frac{\left({\lambda }_6-{\lambda }_3\right){\sigma }^2}{\mathit{\text{TKN}}}{\mathit{\text{J}}}_T,$$ (11)

with

$${\mathit{\text{E}}}_i=2{\mathit{\text{I}}}_T+2\text{ exp}\left\{\frac{\left(1-{\lambda }_1\right){\sigma }^2}{2}\right\}\text{diag}\left\{\text{cosh}\left({\beta }_1+X_{i1}\delta \right),\dots ,\text{cosh}\left({\beta }_T+X_{\mathit{\text{iT}}}\delta \right)\right\},$$ (12)

and λ₁, λ₃, and λ₆ are three eigenvalues of the extended block exchangeable correlation matrix defined in Lemma 1. Unlike Theorem 1, Equations (11) and (12) suggest the variance of the intervention effect in a logistic linear mixed model depends on the ICCs through an additional eigenvalue λ₁. In Web Figure 1, we study the relationship between the five ICCs and $\text{var}(\widehat{\delta })$ and confirm that the observations in Theorem 1 remain valid under a logistic linear mixed model with the exception of the within-subject autocorrelation, α₂, for which larger values will lead to more conservative sample size estimates. In Web Appendix D, we provide the expression of E_i for a count outcome with canonical log link and gamma outcome with a canonical inverse link which can be easily computed without complex numerical integration.

3.3 |. Extension to unequal cluster sizes

In multilevel SW-CRTs, it may not always be realistic to assume equal cluster sizes for power calculation. To extend our procedure to unequal cluster sizes, we assume the number of subclusters and the subcluster size only vary across clusters but remain constant within each cluster over time; namely, K_ij = K_i and N_ijk = N_i. A similar assumption was made in previous studies incorporating unequal cluster sizes in sample size calculations for SW-CRTs (Harrison et al., 2019; Matthews, 2020). This assumption is considered appropriate because the efficiency of SW-CRTs is primarily driven by the between-cluster imbalance rather than the within-cluster imbalance over time (Tian et al., 2021). For given I and T and assuming $K_i~f_K\left(K_i;\overline{K},{\text{CV}}_K\right)$ and $N_i~f_N\left(N_i;\overline{N},{\text{CV}}_N\right)$, where f(•; a, b) represents a valid density or mass function with mean a and coefficient of variation (CV) b, the expected variance of $\widehat{\delta }$ can be used for sample size determination and is given by

$$\begin{gathered} \text{var}\left(\widehat{\delta }\right)=\int \dots \int \text{var}(\widehat{\delta }\mid \mathcal{O})\prod _{i=1}^I \\ \times \left\{f_K\left(K_i;\overline{K},{\text{CV}}_K\right)f_N\left(N_i;\overline{N},{\text{CV}}_N\right)d{K}_{i}d{N}_i\right\}, \end{gathered}$$ (13)

where $\mathcal{O}=\left\{\left(K_i,N_i\right),i=1,\dots ,I\right\}$ represents a specific design with unequal cluster sizes and $\text{var}(\widehat{\delta }\mid \mathcal{O})$ can be efficiently computed based on a modified version of Lemma 3 provided in Web Appendix E. To obtain $\text{var}(\widehat{\delta })$, one can impose any sensible parametric distributions for f_K and f_N and approximate (13) via Monte Carlo integration. For example, one can assume f_K and f_N as gamma distributions with specified mean and CV. A total of R sets of cluster size configurations, $\left\{{\mathcal{O}}^{(r)},r=1,\dots ,R\right\}$, are then drawn from the specified gamma distributions (rounded to nearest integer) to obtain $\text{var}(\widehat{\delta })\approx R^{-1}{\sum }_{r=1}^R\text{var}\left(\widehat{\delta }\mid {\mathcal{O}}^{(r)}\right)$. By averaging over R designs (e.g., R = 1000), $\text{var}(\widehat{\delta })$ accounts for the anticipated variations in cluster sizes and can be used in (2) for power calculation. Finally, when CV_K = CV_N = 0, the above procedure coincides with that in Sections 3.1 and 3.2 as both f_K and f_N degenerate to a point mass. Additional details are provided in Web Appendix E.

4 |. SIMULATION STUDY

We conducted a simulation study to assess the accuracy of our sample size procedures for a Gaussian outcome and a binary outcome. For illustration, we focused on a closed-cohort design at the subcluster level and a cross-sectional design at the subject level (design (B)). We generated correlated Gaussian outcomes based on the linear mixed model, Y_ijkl = β_j + δX_ij + b_i + c_ik + s_ij + π_ijk + ϵ_ijkl, by constraining the total variance components σ² = 1. Given σ², we consider three sets of ICCs (recall that α₂ = α₁ under design (B)), (α₀, α₁, ρ₀, ρ₁) = {(0.1, 0.05, 0.025, 0.0125), (0.03, 0.015, 0.0075, 0.00375), (0.01, 0.005, 0.0025, 0.00125)}, which determines the value of each variance component. The within-period ICCs were chosen to mimic commonly reported values in parallel-arm CRTs, and the between-period ICCs correspond to a CAC of 0.5. By Theorem 1, $\text{var}(\widehat{\delta })$ is invariant to the period effects, and therefore we only considered a gently increasing secular trend with β₁ = 0 and β_j+1 − β_j = 0.1 × (0.5)^j−1 for j ≥ 1. On the other hand, we generated correlated binary outcomes from a Bernoulli distribution with Y_ijkl ~ Bern(μ_ijkl), with μ_ijkl = 1/{1 + exp(−β_j − δX_ij − b_i − c_ik − s_ij − π_ijk)}. Following Li et al. (2018), we assumed a slightly decreasing secular trend on the logit scale with a baseline prevalence of 0.7 such that β₁ = 1/{1 + exp(−0.7)} and β_j − β_j+1 = 0.1 × (0.5)^j−1 for j ≥ 1. To specify the variance components, we employ the latent response formulation in Section 3.2 by setting the residual variance as π²/3 and mapping the three sets of ICCs considered for Gaussian outcomes to the variance components on the logit scale (Web Appendix F).

We simulated standard stepped wedge designs such that an equal number of clusters crossed over to treatment at a randomly assigned step. Motivated by a recent systematic review of SW-CRTs (Grayling et al., 2017) and assuming equal cluster sizes, we varied the number of clusters (I) from eight to 30, the number of subclusters per cluster (K) from two to six, the number of periods (T) from four to seven, and allowed a maximum of 15 subjects per subcluster (N). For Gaussian outcomes, we assumed standardized effect sizes, δ/σ ∈ {0.1, 0.2, 0.25, 0.35, 0.4, 0.5}, and for binary outcomes, we considered effect sizes on the odds ratio scale, exp(δ) ∈ {0.8, 0.75, 0.7, 0.65, 0.6, 0.5}. Each specific parameter combination was selected to ensure the predicted power is at least 80% based on a two-sided 5% level Wald test. For a Gaussian outcome, the predicted power is based on Equation (2) and Theorem 1; for a binary outcome, the predicted power is based on Equation (2), Lemma 3, and Equations (11) and (12). The empirical power of the test is obtained as the proportion correctly rejecting H₀ over 1000 simulated SW-CRTs, and the agreement between the predicted and empirical power was used to confirm the accuracy of the proposed method. Finally, we assessed the empirical type I error rate to confirm the validity of the Wald test. For this purpose, we simply set δ/σ = 0 with a Gaussian outcome and exp(δ) = 1 with a binary outcome. Further, in Web Tables 3 and 4, we compare the predicted power assuming correctly CAC = 0.5 with the predicted power assuming equal within- and between-period ICCs (incorrectly assuming CAC = 1). Our results show that incorrectly assuming equal within- and between-period ICCs typically leads to overly confident power predictions. Finally, to assess the accuracy of our approach in Section 3.3 with unequal cluster sizes, we chose four typical scenarios and draw K_i and N_i from gamma distributions with CV_K ∈ {0, 0.25, 0.5} and CV_N ∈ {0, 0.25, 0.5, 0.75, 1.0}.

4.1 |. Simulation results for Gaussian outcomes

We present the empirical type I error rate and empirical and predicted power of the Wald test under each scenario with a Gaussian outcome (Table 2). We used the restricted maximum likelihood estimator for model fitting, based on which the Wald test is carried out. The empirical type I error rate was generally conservative, and the empirical and predicted power were in agreement with the largest difference within 3%. Similar results were found when the Wald test was computed from (unrestricted) maximum likelihood estimation (Web Table 5). Lastly, in Web Tables 6 and 7 we present the simulation results under unequal cluster sizes. The empirical type I error rate was conservative overall, and differences between empirical and predicted power were within −4.4% and 3.5%.

TABLE 2.

Estimated required number of clusters I, subclusters per cluster K, participants per subcluster N, periods T, empirical type I error (Test Size), empirical power (Empirical), and predicted power (Predicted) obtained from sample size formula for given effect size δ/σ, within-period ICCs for within- and between-subcluster (α₀, ρ₀), and between-period ICCs for within- and between-subcluster (α₁, ρ₁) assuming a cluster autocorrelation of 0.5, when outcome is Gaussian (n = 1000)

δ/σ	(α0, ρ0)	(α1, ρ1)	I	K	N	T	Test Size	Empirical	Predicted
0.1	(0.03, 0.0075)	(0.015, 0.00375)	24	6	15	7	3.6	88.2	85.3
	(0.01, 0.0025)	(0.005, 0.00125)	30	6	15	4	4.3	82.5	82.2
			24	5	10	7	4.4	82.9	81.4
0.2	(0.1, 0.025)	(0.05, 0.0125)	24	6	10	4	4.5	85.4	83.3
			18	3	12	7	3.9	84.0	81.8
	(0.03, 0.0075)	(0.015, 0.00375)	18	3	15	4	3.2	81.3	80.0
			15	3	10	6	4.0	81.1	80.8
	(0.01, 0.0025)	(0.005, 0.00125)	12	6	10	4	2.8	82.2	82.6
			10	4	10	6	2.7	79.4	80.0
0.25	(0.1, 0.025)	(0.05, 0.0125)	21	4	10	4	5.2	83.7	84.6
			18	2	10	7	4.6	83.2	83.5
	(0.03, 0.0075)	(0.015, 0.00375)	15	4	8	4	2.7	82.9	81.4
			12	2	10	7	3.5	81.0	80.2
	(0.01, 0.0025)	(0.005, 0.00125)	24	2	8	4	4.1	83.7	84.3
			10	3	9	6	1.8	83.6	83.6
0.35	(0.1, 0.025)	(0.05, 0.0125)	12	4	9	4	2.8	84.5	83.2
			10	3	8	6	1.9	83.6	82.9
	(0.03, 0.0075)	(0.015, 0.00375)	9	3	12	4	2.4	84.3	83.5
			16	2	5	5	3.0	86.9	84.0
	(0.01, 0.0025)	(0.005, 0.00125)	9	3	9	4	2.5	82.1	82.9
			8	3	7	5	1.7	77.7	80.0
0.4	(0.1, 0.025)	(0.05, 0.0125)	18	2	7	4	3.2	87.9	86.2
			12	2	8	5	3.5	80.8	82.0
	(0.03, 0.0075)	(0.015, 0.00375)	9	3	8	4	1.4	80.8	82.5
			8	3	7	5	1.1	84.3	83.5
	(0.01, 0.0025)	(0.005, 0.00125)	15	2	5	4	3.3	81.2	83.3
			12	2	5	5	1.8	85.4	85.1
0.5	(0.1, 0.025)	(0.05, 0.0125)	12	2	7	4	3.3	82.6	84.7
			12	2	4	5	3.2	84.3	82.5
	(0.03, 0.0075)	(0.015, 0.00375)	9	2	8	4	1.8	87.4	85.4

4.2 |. Simulation results for binary outcomes

We present the empirical type I error rate, and empirical and predicted power of the Wald test under each scenario using the logistic linear mixed model fitted via the Laplace approximation (Table 3). Similarly, the empirical type I error rate was well controlled under the nominal level, and the empirical power was in agreement with the predicted power, with the differences ranging from −0.9% to 5.3%. This suggests that our sample size procedure based on first-order Taylor expansion at most results in slightly conservative power prediction. Results were similar when penalized quasi-likelihood (which is computationally more efficient) was used to fit the model (Web Table 8). Lastly, in Web Tables 9 and 10, we present the simulation results under unequal cluster sizes. Overall, the empirical type I error rate was adequately controlled and differences between empirical and predicted power were within −6.1% and 8.2%. Overall, these results confirm that the procedure in Section 3.3 sufficiently captures the trend of the empirical power under unequal cluster sizes.

TABLE 3.

Estimated required number of clusters I, subclusters per cluster K, participants per subcluster N, periods T, empirical type I error (Test Size), empirical power (Empirical), and predicted power (Predicted) obtained from sample size formula for given effect size exp(δ), within-period ICCs for within- and between-subcluster (α₀, ρ₀), and between-period ICCs for within- and between-subcluster (α₁, ρ₁) assuming a cluster autocorrelation of 0.5, when outcome is binary with canonical logit link (n = 1000)

exp(δ)	(α0, ρ0)	(α1, ρ1)	I	K	N	T	Test Size	Empirical	Predicted
0.8	(0.03, 0.0075)	(0.015, 0.00375)	18	6	15	7	4.2	82.2	80.7
	(0.01, 0.0025)	(0.005, 0.00125)	27	6	15	4	5.2	85.3	84.2
			25	4	12	6	2.7	81.2	81.0
0.75	(0.1, 0.025)	(0.05, 0.0125)	25	6	15	6	5.2	85.8	82.8
			24	5	15	7	4.6	88.1	83.1
	(0.03, 0.0075)	(0.015, 0.00375)	27	5	12	4	5.1	83.4	80.6
			30	3	10	6	5.2	84.0	83.3
	(0.01, 0.0025)	(0.005, 0.00125)	21	6	10	4	2.8	82.0	80.5
			12	4	15	7	2.4	84.6	81.5
0.7	(0.1, 0.025)	(0.05, 0.0125)	30	5	14	4	4.4	82.9	82.3
			18	4	15	7	4.2	86.7	81.7
	(0.03, 0.0075)	(0.015, 0.00375)	18	6	10	4	4.8	82.7	80.6
			15	3	15	6	4.4	82.7	81.2
	(0.01, 0.0025)	(0.005, 0.00125)	18	4	12	4	3.6	83.2	82.3
			20	2	15	5	3.9	81.5	81.8
0.65	(0.1, 0.025)	(0.05, 0.0125)	21	6	12	4	4.1	88.3	83.6
			18	3	12	7	3.9	87.6	84.1
	(0.03, 0.0075)	(0.015, 0.00375)	24	3	10	4	4.6	86.4	85.0
			20	2	10	6	3.3	85.7	83.7
	(0.01, 0.0025)	(0.005, 0.00125)	15	4	10	4	2.5	84.8	82.7
			12	3	14	5	3.1	85.4	85.2
0.6	(0.1, 0.025)	(0.05, 0.0125)	18	5	10	4	3.6	85.9	82.3
			12	3	15	7	4.6	88.1	82.8
	(0.03, 0.0075)	(0.015, 0.00375)	16	2	12	5	4.6	85.3	83.9
			15	2	10	6	3.7	87.1	84.0
	(0.01, 0.0025)	(0.005, 0.00125)	21	2	10	4	3.7	84.6	85.5
			12	3	8	5	2.4	81.6	80.0
0.5	(0.1, 0.025)	(0.05, 0.0125)	15	3	10	4	3.0	86.9	83.2
			16	2	9	5	3.3	84.7	82.5
	(0.03, 0.0075)	(0.015, 0.00375)	15	2	9	4	2.6	88.2	84.1

5 |. APPLICATIONS TO SW-CRTs WITH SUBCLUSTERS

5.1 |. Lumbar Imaging with Reporting of Epidemiology trial

The LIRE trial aimed to evaluate the effect of adding prevalence data to spine imaging reports on subsequent spine-related health care utilization (Jarvik et al., 2015). The study planned to randomize I = 100 practices consisting of a total of 1700 primary care providers (PCPs) over T = 6 periods; each practice is a cluster and each PCP represents a subcluster. This is a closed-cohort design on the subcluster level but a cross-sectional design at the subject level (design (B)). While the number of PCPs per practice varied, we assume K = 17 PCPs per practice for illustration. The primary outcome was log-transformed spine-related relative value units (RVUs), a continuous composite measure of back pain. Assuming the median and total variance of RVU is approximately 3.56 and 2.5 (Jarvik et al., 2020), a 5% reduction in median due to treatment corresponds to a standardized effect size of around −0.1. Based on preliminary data, an overall ICC was estimated to be 0.013 with a 95% confidence interval of (0.00, 0.046). We therefore assume the within-period within-PCP ICC to be the upper bound of the preliminary estimates, α₀ = 0.046, and a slightly smaller within-period between-PCP ICC of ρ₀ = 0.04. Assuming a CAC of 0.5 further gives us α₁ = 0.023 and ρ₁ = 0.02. Based on (2) and our variance expression (5), we found having N = 77 subjects per PCP leads to 87.5% power for a two-sided 5% test.

To assess the sensitivity of our power calculation to ICC specifications, we looked at power trends for α₀ ∈ (0, 0.1) with various ratios of ρ₀/α₀ across varying levels of CAC (0.2, 0.5, 0.8). In concordance with our findings in Theorem 1, larger within-period ICCs (α₀, ρ₀) and smaller between-period ICCs (α₁, ρ₁) correspond to more conservative power predictions (Figure 3), thus we are confident that our ICC specifications likely produced a conservative power estimate. Alternatively, we have also derived a DE based on the closed-form variance expression (5) for sample size determination. The details and illustrative calculations that reach the same power results in the LIRE trial are provided in Web Appendix G. Further, in Web Appendix H we provide sample size determinations for the LIRE trial under alternative cluster level designs. Finally, in Web Appendix I we provide an application to the LIRE trial assuming unequal cluster sizes using the expected variance expression (13).

FIGURE 3.

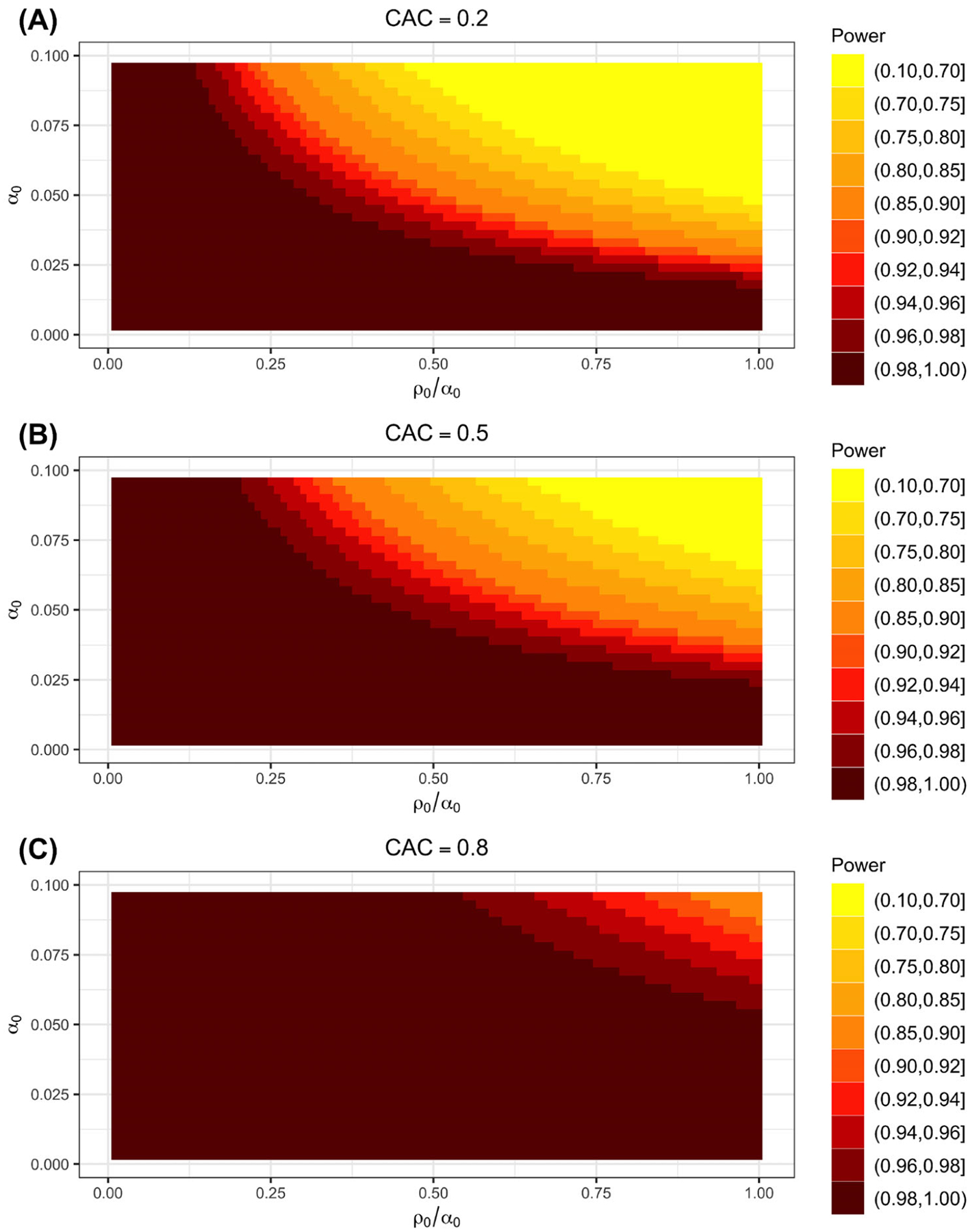
Contour plots illustrating the relationship between ICCs and power in our application study of the LIRE trial. ICCs include: within-period within-subcluster α₀; between-period within-subcluster α₁; within-period between-subcluster ρ₀; and between-period between-subcluster ρ₁. Various α₀ specifications are shown on the y-axis and various ρ₀ specifications are shown on the x-axis as a ratio of α₀. Between-period specifications are denoted by the CAC. Darker colors correspond to higher values of power

5.2 |. Washington State EPT trial

In the Washington State EPT study, investigators were interested in evaluating whether an expedited partner therapy, the treatment of sex partners of people with sexually transmitted infections without medical evaluation, would decrease the risk of chlamydia reinfection (Golden et al., 2015). Since the chlamydia infection status was binary, we illustrate the following calculations with a logistic linear mixed model. The study included I = 24 LHJ that were randomly assigned to intervention at one of four steps (T = 5). Each LHJ includes clinics that provide subject-level outcomes over time. Of the clinics with repeated measures, over half were sampled at each period; thus for simplicity, we assume a closed-cohort design at the clinic level and a cross-sectional design at the subject level (design (B)). A total of 219 clinics participated in chlamydia testing, but to be conservative we assume the number of clinics per LHJ is K = 5. In the design of this study, investigators aimed to detect a prevalence ratio of 0.7 and assumed a baseline prevalence of 0.05. Because the outcome is rare, we assume the effect size expressed as an odds ratio can be approximated by the prevalence ratio and obtain the required number of subjects per clinic (N) to achieve at least 80% power for a two-sided 5% test. Without distinguishing between clusters and subclusters, Li et al. (2021) estimated the within-period ICC to be 0.007 and the between-period ICC to be 0.004 based on marginal models. We consider these values to be the within-period between-clinic and between-period within-clinic ICCs (defined based on the latent response formulation in Section 3.2) such that ρ₀ = 0.007 and α₁ = 0.004, and set the remaining ICCs to be α₀ = 0.008 and ρ₁ = 0.0035 (corresponding to a CAC of 0.5). We assume a slightly decreasing time effect as in our simulations and find based on Equation (2), Lemma 3, and Equations (11) and (12) that including N = 42 subjects per clinic gives us 89.5% power. As a sensitivity analysis, we considered a larger decreasing period effect such that β_j − β_j+1 = 1 × (0.5)^j−1 for j ≥ 1, which increased N = 139 to attain 89.5% power. On the other hand, using a smaller decreasing period effect, β_j − β_j+1 = 0.01 × (0.5)^j−1 for j ≥ 1, reduced our required number of subjects per clinic to N = 37 to achieve 89.3% power.

We assessed the sensitivity of our power calculation to ICC specifications by examining the power trends for varying α₀ ∈ (0, 0.05) with various ratios of ρ₀/α₀ across varying levels of CAC (0.2, 0.5, 0.8) and time trends (β_j − β_j+1 = {0.01, 0.1, 1} × (0.5)^j−1 for j ≥ 1) (Web Figure 2). We found that larger within-period ICCs (α₀, ρ₀) and smaller between-period ICCs (α₁, ρ₁) correspond to more conservative power predictions, thus our current ICC specifications likely produced a conservative power estimate. Furthermore, in Web Appendix J we provide sample size determinations for the EPT study under alternative cluster level designs. Finally, in Web Appendix K we provide an application to the EPT study assuming unequal cluster sizes using the expected variance expression (13).

6 |. CONCLUDING REMARKS

In this study, we presented new sample size procedures for SW-CRTs with subclusters. With a Gaussian outcome, we characterized an extended block exchangeable correlation structure induced by the random-effects assumption of the linear mixed model. The extended block exchangeable correlation structure is parameterized by at most five ICC parameters and intentionally differentiate between the within-period and between-period ICCs to avoid unrealistically small sample size estimates (Taljaard et al., 2016). We derived the variance of the intervention effect estimator, which depends on the ICC parameters only through two eigenvalues of the extended block exchangeable correlation matrix. Assuming a GLMM with non-Gaussian outcomes, we further presented a generic framework for approximating the variance of the intervention effect, and specific examples are provided under the canonical link functions. Of note, while our primary focus is GLMMs, our methods can be extended to accommodate generalized estimating equations; the details are presented in Web Appendix L.

While our sample size and variance expressions are derived based on large sample approximation, many SW-CRTs may have a limited number of clusters. Our simulation results suggest that with as few as eight clusters, a Wald t-test can preserve adequate type I error rate and maintain sufficient power, thus validating our methods. To sum up, we reiterate two key contributions from this work. First, our variance expressions are computationally convenient, thus obviating the need for simulation-based power calculation; the latter approach can quickly become impractical in SW-CRTs with subclusters due to the need for searching across many design parameters, as well as the associated computational cost for repeatedly fitting complex multilevel models. Second, we have characterized the relationship between various ICCs and power in the presence of subclusters and confirmed that assuming smaller between-period ICCs typically leads to larger and conservative sample sizes. In the presence of limited external data to inform sample size calculations in SW-CRTs with subclusters, it may therefore be prudent to assume smaller between-period ICC values.

DATA AVAILABILITY STATEMENT

Data sharing is not applicable to this article as no new data were created or analyzed in this paper.