Figure 4. Growth‐lag model uses the tradeoff between Aci2’s fast growth and Pa’s short lag to explain two‐resource coexistence.

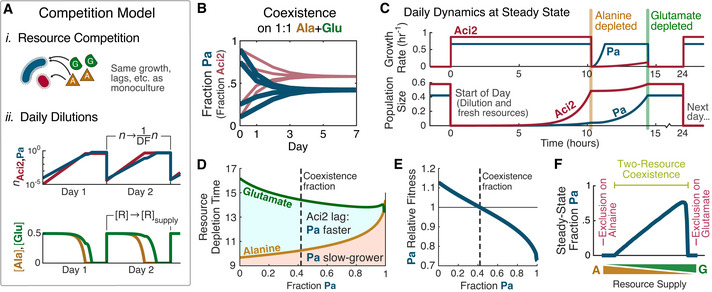
1. The competition model is an extension of the monoculture model. (i) Species have the same growth, lags, and resource consumption as in monocultures, but now compete for the same resource pool. (ii) After saturation, population sizes are divided by the dilution factor (10⁴ in this figure) and resource concentrations are reset to the supply concentrations. (Modeling details in Materials and Methods.)
2. With parameters matching those used experimentally in Fig 1C, the growth‐lag model predicts coexistence of Aci2 and Pa on alanine and glutamate, as observed in competition experiments.
3. Model prediction of growth rates and population sizes over the course of 1 day after the 1:1 alanine:glutamate co‐culture has reached steady state. Pa starts the day with a population fraction of 0.42, declines to a population fraction of 0.07 at alanine depletion, and recovers to a population fraction of 0.42 by the time glutamate is depleted.
4. The alanine and glutamate resource depletion times vary with the (start‐of‐day) population fractions due to different resource preferences and initial growth rates.
5. These variations modulate the relative fitness of the two strains and in doing so facilitate a negative‐frequency dependent interaction that stabilizes coexistence. Relative Fitness of Pa is calculated as its fold growth over the course of a day divided by Aci2’s fold growth (Materials and Methods), and shown as a function of its population fraction at the start of the day.
6. The model predicts the competitive outcome will depend on the resource supply fractions with exclusion occurring as the supply approaches entirely alanine or entirely glutamate.