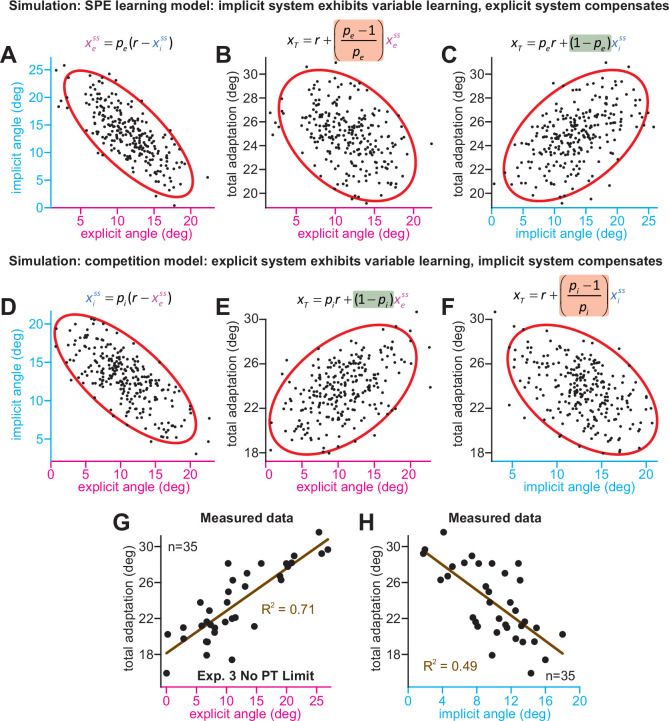
Figure 5. Implicit-explicit correlations with total adaptation match the competition theory.
The competition equation states that xiss = pi(r – xess), where pi is a scalar learning gain depending on ai and bi. The competition between steady-state implicit (xiss) and explicit (xess) adaptation predicted by this model is simulated in D across 250 hypothetical participants. The model pi is fit to data in Experiment 3. Total learning is given by xTss = xiss + xess. These two equations can be used to derive expressions relating total learning (xTss) to steady-state implicit (xiss) and explicit (xess) learning. In E, we show that the competition theory predicts a positive relationship between explicit learning and total adaptation (equation at top derived in Appendix 7, green denotes a positive gain). In F, we show that the competition theory predicts a negative relationship between implicit learning and total adaptation (equation at top derived in Appendix 7, red shading denotes negative gain). In (A–C), we consider an alternative model. Suppose that implicit learning is immune to explicit strategy and varies independently across participants. This is equivalent to the SPE learning model. But in this case, the explicit system could respond to variability in implicit learning via another competition equation: xess = pe(r – xiss). Here, pe is an explicit learning gain (must be less than one to yield a stable system). In A, we show the negative relationship between implicit and explicit adaptation predicted by this alternate SPE learning model. In B, we show that when the explicit system responds to implicit variability (SPE learning) there is a negative relationship between total adaptation and explicit strategy. The equation at top is derived in Appendix 7. In C, we show that the SPE learning model will yield a positive relationship between implicit learning and total adaptation. Equation at top derived in Appendix 7. (G) We measured the relationship between explicit strategy and total adaptation in Exp. 3 (No PT Limit group). Total learning exhibits a positive correlation with explicit strategy. (H) Same concept as in G, but here we show the relationship between total learning and implicit adaptation. The patterns in G and H are consistent with the competition theory (compare with E and F).
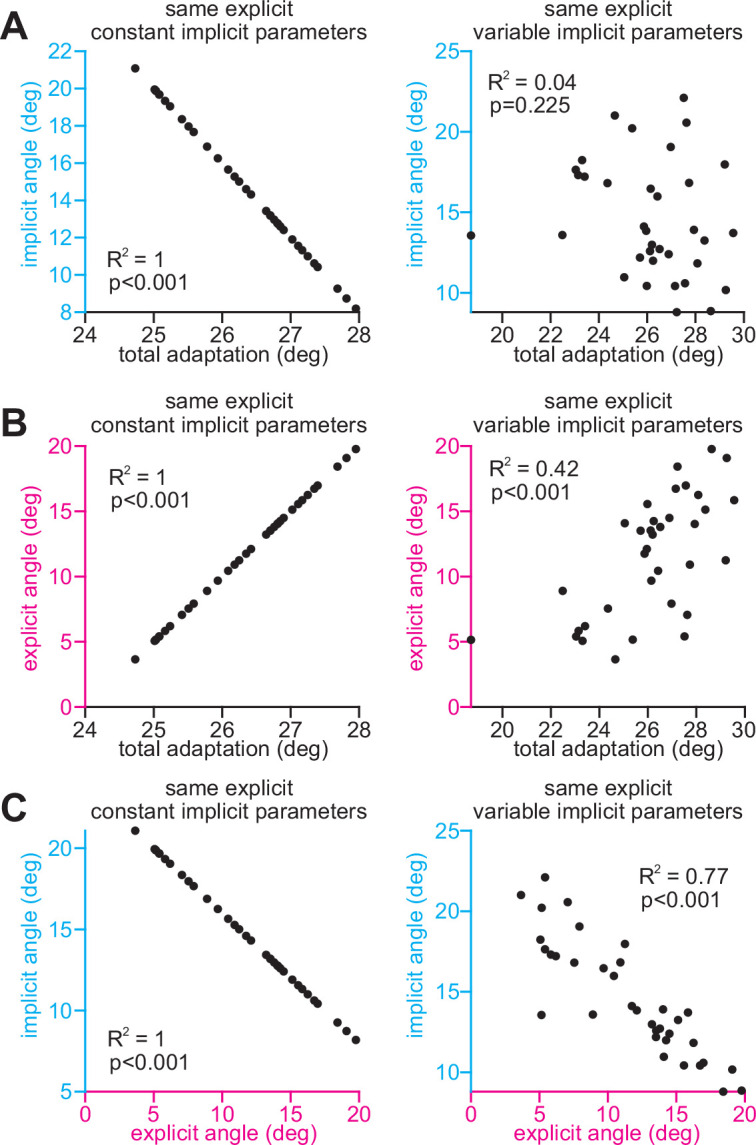
Figure 5—figure supplement 1. Relationships between implicit, explicit, and total learning indicate competition.
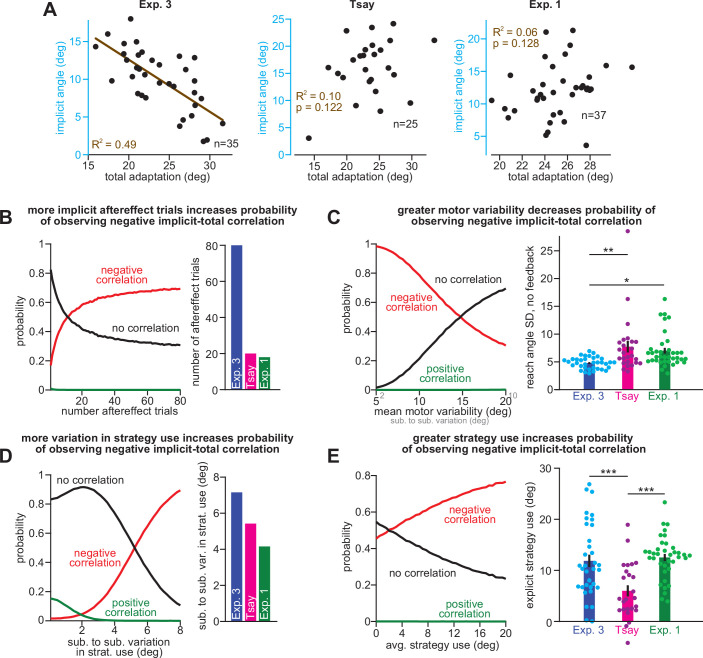
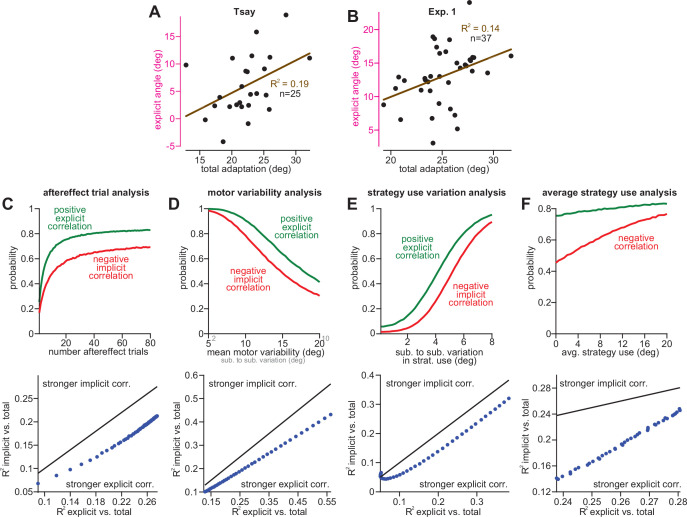
Figure 5—figure supplement 2. Factors that weaken the correlation between implicit learning and total adaptation.
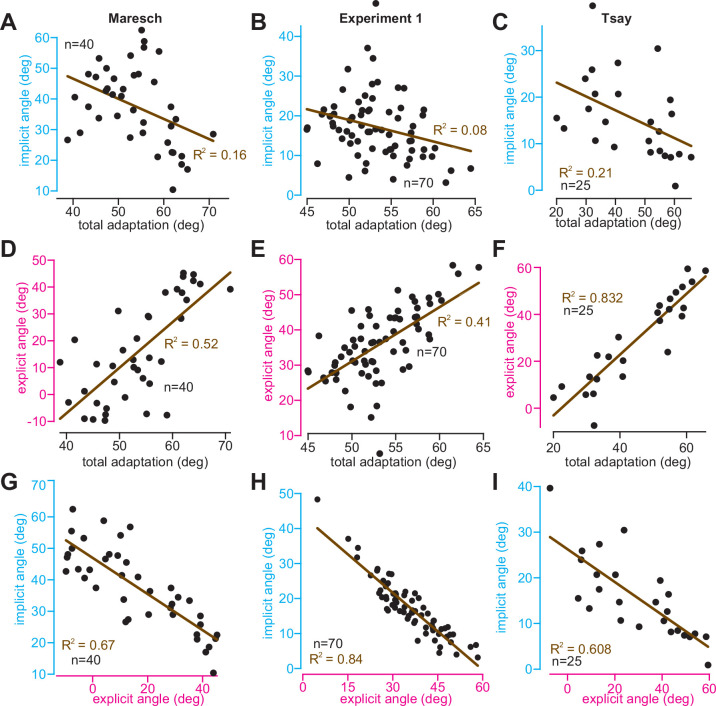
Figure 5—figure supplement 3. Correlations between explicit learning and total adaptation are more robust to between-subject implicit variability.
Figure 5—figure supplement 4. Variance in implicit learning properties weakens the relationship between implicit learning and total adaptation in the competition theory.