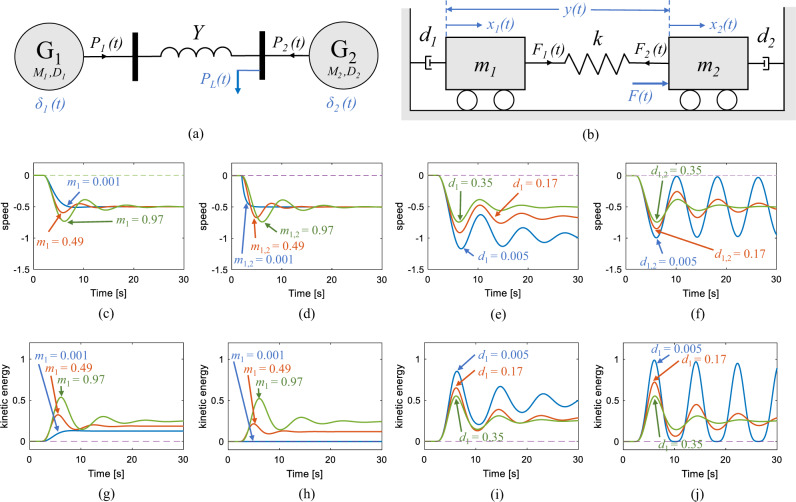
Fig. 2. Mechanical analog of synchronized operation of generators in an electric power network.
a An electrical power network with two generators, G1 and G2, whose inertia and damping coefficients are M1, M2, D1, and D2, respectively. The two generators are interconnected through a transmission line with an admittance value of Y and respond to the changes of demand of electric load PL. b A mechanical analog of the electrical power network with two bodies of mass m1 and m2 tied to their nearest wall with dampers d1 and d2, respectively. The bodies of mass are interconnected via a spring with constant of k and respond to the external force F. Default values for constants in this network are m1 = m2 = 1.00, d1 = d2 = 0.35, and k = 0.30. The mechanical network here is subjected to an external force F and while the default values are kept unchanged, only one or two values are varied in order to conduct a parametric sensitivity analysis of the response. c, g Dynamics of speed and kinetic energy for varying values of m1, heterogeneous inertial mass condition. d, h Dynamics of speed and kinetic energy for varying values of m1 and m2, homogeneous inertial mass condition. e, i Dynamics of speed and kinetic energy for varying values of d1, heterogeneous damping condition. f, j Dynamics of speed and kinetic energy for varying values of d1 and d2, homogeneous damping condition. These results indicate that mechanical networks with a smaller inertial mass (all Blue traces in c, d, g, h) and greater damping characteristics (all Green traces in e, f, i, j) offer a more robust and stable natural synchronization capability, as the speed reaches an equilibrium faster and the kinetic energy is dissipated quicker.