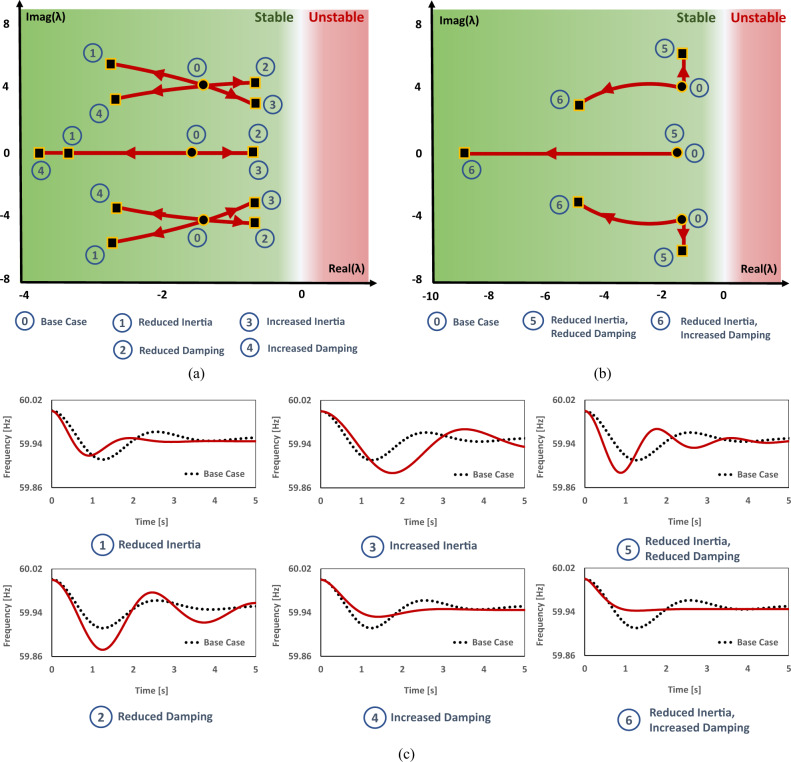
Fig. 3. Loci of migration of eigenvalues in the complex plane and time-domain response as generator parameters are varied.
a Individual parameter changes, b concurrent parameter changes that replicated technological changes, c time-domain dynamic response. We analyzed the sensitivity of eigenvalues of a non-reference generator to parametric changes and the network coupling mode in the 3-generator network as a benchmark. For the base case, Mi = (1.59, 0.80, 0.32) and Di = (1.53, 1.53, 0.92). For the network data see Supplementary Note 6. We considered six scenarios in addition to the base case. In each scenario, one or more parameters were changed by an order of 2. All plots shown include two internal modes that yield a pair of complex conjugate eigenvalues one coupling mode that is a pure real eigenvalue. In time-domain results, the higher the nadir frequency is, the more robust the frequency dynamic response (see Supplementary Note 8, for the characterization of frequency response trace). The results from individual parametric analysis here concluded that the reduction of inertia and the increase of damping moves the imaginary part of internal modes further away from the y-axis, resulting in an improved dynamic response, while the increase of inertia and reduction of damping has the opposite impact. For concurrent parametric analyses; scenario 5 represents the substitution of a synchronous generator with a grid-following (GFL) inverter and scenario 6 represents the replacement with a multi-loop droop grid-forming (GFM) inverter. These results exhibit the superior capability of the multi-loop droop GFM over GFL in improving the network dynamics. The GFM-VSM replacement is not presented here because it uses parameters equivalent to those of a synchronous generator and does not vary the result from the synchronous generator (SG) base case.