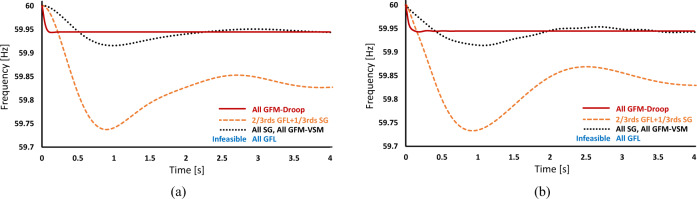
Fig. 4. Validation of the analytical model using a high-order model implemented in an industry-grade power system planning software for electromagnetic transient (EMT) dynamic modeling parameters are varied.
a Results from generic second-order analytical models developed in this paper, b results from full-order models in Power Systems Computer Aided Design (PSCAD), available open-source62. The results here show the dynamic frequency response for a 3-generator, 9-bus network with different generation technologies. There are three main points of note. First, the frequency response for the three scenarios of “All Synchronous Generator (SG)", “All virtual machine grid-forming (GFM-VSM)", and “2/3rd grid-following (GFL)+1/3rd SG" are very similar. Second, operating a network with 100% GFL is infeasible because mathematically, the denominator of the Jacobian elements cannot be zero (100% GFL implies M = 0) and practically, there will be no source to construct the synchronization frequency for the GFLs to follow. Third, and perhaps the most significant point, when operating with 100% multi-loop droop grid-forming (GFM), the effective inertia value is reduced to near zero and the GFM frequency response can be seen effectively as first-order and therefore be less likely to experience severe frequency excursions. This corroborates with the observations reported in ref. 63. The inertia and damping coefficients for these cases and the quantification of their dynamic response are presented in Supplementary Table II.