Pharmacodynamics of Gemifloxacin against Streptococcus pneumoniae in an In Vitro Pharmacokinetic Model of Infection

Abstract

The pharmacodynamics of gemifloxacin against Streptococcus pneumoniae were investigated in a dilutional pharmacodynamic model of infection. Dose fractionation was used to simulate concentrations of gemifloxacin in human serum associated with 640 mg every 48 h (one dose), 320 mg every 24 h (two doses), and 160 mg every 12 h (four doses). Five strains of S. pneumoniae for which MICs were 0.016, 0.06, 0.1, 0.16, and 0.24 mg/liter were used to assess the antibacterial effect of gemifloxacin. An inoculum of 10⁷ to 10⁸ CFU/ml was used, and each experiment was performed at least in triplicate. The pharmacodynamic parameters (area under the concentration-time curve [AUC]/MIC, maximum concentration of drug in serum [C_max]/MIC, and the time that the serum drug concentration remains higher than the MIC [T > MIC]) were related to antibacterial effect as measured by the area under the bacterial-kill curve from 0 to 48 h (AUBKC₄₈) using an inhibitory sigmoid E_max model. Weighted least-squares regression was used to predict the effect of the pharmacodynamic parameters on AUBKC₄₈, and Cox proportional-hazards regression was used to predict the effect of the three pharmacodynamic parameters on the time needed to kill 99.9% of the starting inoculum (T99.9). There was a clear relationship between strain susceptibility and clearance from the model. The simulations (160 mg every 12 h) were associated with slower initial clearance than were the other simulations; in contrast, bacterial regrowth occurred with the 640-mg simulation when MICs were ≥0.1 mg/liter. The percentage coefficient of variance was 19% for AUBKC₄₈, and the inhibitory sigmoid E_max model best fit the relationship between AUBKC₄₈ and AUC/MIC. C_max/MIC and T > MIC fit less well. The maximum response occurred at an AUC/MIC of >300 to 400. In weighted least-squares regression analysis, there was no evidence that C_max/MIC was predictive of AUBKC₄₈, but both AUC/MIC and T > MIC were. A repeat analysis using only data for which the T > MIC was >75% and for which hence regrowth was minimized indicated that AUC/MIC alone was predictive of AUBKC₄₈. Initial univariate analysis indicated that all three pharmacodynamic parameters were predictive of T99.9, but in the multivariate model only C_max/MIC reached significance. These data indicate that gemifloxacin is an effective antipneumococcal agent and that AUC/MIC is the best predictor of antibacterial effect as measured by AUBKC₄₈. However, C_max/MIC is the best predictor of speed of kill, as measured by T99.9. T > MIC also has a role in determining AUBKC₄₈, especially when the dose spacing is considerable. Once-daily dosing seems most suitable for gemifloxacin.

The study of antibacterial pharmacodynamics and the development of the fluoroquinolone drug class have paralleled one another over the last 10 to 20 years. As a result there is a significant body of data on fluoroquinolone pharmacodynamics encompassing an in vitro model and animal and human studies. Three pharmacodynamic parameters are commonly investigated in terms of prediction of antimicrobial effect: the ratio of area under the concentration-time curve to MIC (AUC/MIC), the ratio of maximum concentration of drug in serum to MIC (C_max/MIC), and the time that the serum drug concentration remains higher than the MIC (T > MIC). The majority of data for fluoroquinolones from in vitro models (3, 16, 17), animals (1, 7; Y. Watanabe, S. Ebert, and W. Craig, Program Abstr. 32nd Intersci. Conf. Antimicrob. Agents Chemother., abstr. 42, 1992) and humans (9, 10, 18) indicate that AUC/MIC and/or C_max/MIC determines antibacterial effect. Some in vitro model data indicate that when the intensity of effect is used as the measure of antibacterial effect, the fluoroquinolone half-life in serum and, hence, T > MIC have a significant effect on efficacy (8; A. Firsov and S. Zinner, 8th Int. Symp. New Quinolones, p. 7, 1998). Recently it has been proposed that AUC/MIC or C_max/MIC is not predictive of fluoroquinolone antibacterial effect in gram-positive bacteria, unlike in gram-negatives (D. H. Wright, L. B. Horde, M. Peterson, A. D. Hoang, and J. C. Rotschafer, Abstr. 98th Gen. Meet. Am. Soc. Microbiol., abstr. A-86, p. 53, 1998), and that if AUC/MIC is the dominant pharmacodynamic parameter its magnitude may be less for Streptococcus pneumoniae than for aerobic gram-negative rods (11–13).

Gemifloxacin, previously SB-265805, is a developmental fluoroquinolone notable for its marked in vitro potency against gram-positive pathogens such as S. pneumoniae: it has a MIC at which 90% of the isolates tested are inhibited of 0.03 to 0.06 mg/liter (L. M. Kelly, M. R. Jacobs, and P. C. Appelbaum, Abstr. 38th Intersci. Conf. Antimicrob. Agents Chemother., abstr. F-87, 1998; M.-Y. Kim, K.-S. Paek, and Y. S. Choo, Abstr. 38th Intersci. Conf. Antimicrob. Agents Chemother., abstr. F-93, 1998). Human pharmacokinetic studies of a 320-mg oral dose in young, healthy volunteers indicate a C_max after 1 h, an AUC of 9.1 mg · h/liter, and a half-life of 7 to 8 h (A. Allen, E. Bygate, and M. Teillol-Foo, 21st Int. Congr. Chemother., abstr. P-440, p. 137, 1999). Thus far, there have been few published studies on gemifloxacin's pharmacodynamic properties, but it is thought to be typical of the fluoroquinolone class in exhibiting concentration-dependent killing and persistent antibacterial effects against S. pneumoniae (6).

In this study we used a dilutional in vitro pharmacodynamic model, five strains of S. pneumoniae for which gemifloxacin MICs were different, and a dose fractionation design to establish the pharmacodynamic parameters best related to antibacterial effect. Subsequently we defined the magnitude of the pharmacodynamic parameters required to produce the maximal effect.

(This work was presented in part at the 39th Interscience Conference on Antimicrobial Agents and Chemotherapy, San Francisco, Calif., September 1999).

MATERIALS AND METHODS

Models.

A New Brunswick Bioflo 1000 (Hatfield, Hertfordshire, United Kingdom) in vitro model was used to simulate the concentrations in serum associated with the oral administration of 320 mg of gemifloxacin every 24 h, 640 mg (one dose) every 48 h, and 160 mg every 12 h, all for 48 h. The apparatus consists of a single central culture chamber which is connected to a dosing chamber, which in turn is connected to a reservoir containing broth and, secondly, to a vessel collecting outflow from the chamber. The dosing chamber and central culture chamber were diluted with brain heart infusion broth with a peristaltic pump (Ismatec; Bennett & Co., Weston-super-Mare, United Kingdom) at a flow rate of 35 ml/h. The temperature was maintained at 37°C, and the broth in the dosing and central chambers was agitated by a magnetic stirrer at 90 g.

Media.

A 75% brain heart infusion broth (Oxoid, Basingstoke, United Kingdom) was used for all experiments. One percent magnesium chloride (BDH; Poole, Dorset, United Kingdom) was incorporated into nutrient agar plates (Merck, Dorset, United Kingdom) containing 5% whole horse blood (TCS Microbiology, Buckingham, United Kingdom) to neutralize the gemifloxacin before viable counts were determined.

Strains.

S. pneumoniae SMH 18964, SMH 18330, SMH 18327, SMH 18907, and SMH 18329 were used. Strains 18330, 18327, and 18329 were provided by G. Woodnutt, SmithKline Beecham Pharmaceuticals.

Antibiotic.

Gemifloxacin (SB-265805, LB 20304a) was obtained from SmithKline Beecham Pharmaceuticals, Philadelphia, Pa. Stock solutions were prepared according to British Society of Antimicrobial Chemotherapy Guidelines (4) and were stored at −70°C.

MICs and MBCs.

MICs were determined by the British Society of Antimicrobial Chemotherapy-defined standard broth dilution method (4), with the exception that gemifloxacin concentrations decreased in 0.02- or 0.2-mg/liter steps that did not double dilutions. Minimum bactericidal concentrations (MBCs) were determined by a 99.9% reduction in the initial viable count after 24 h.

Pharmacokinetic and bacterial-killing curves.

The in vitro activities of various gemifloxacin concentrations against the five strains described were tested in the model described above. The target peak (C_max) serum gemifloxacin concentration was 1.1 mg/liter at 1.5 h, and the AUC from 0 to 24 h (AUC_0–24) was 8.7 mg · h/liter for the 320-mg dose. Concentrations were simulated to conform closely to the known time profile for concentrations in serum. The 640-mg and 160-mg dose simulations were extrapolated from this. For the 640-mg dose, the C_max was 2.1 mg/liter and the AUC_0–48 was 17.3 mg · h/liter, while for the 160-mg dose, the C_max was 0.6 mg/liter and the AUC_0–12 was 4.8 mg · h/liter. The half-life was 7 h in all simulations. For all experiments, 100 μl of an overnight broth suspension of the test organism was inoculated into the central culture chamber (360-ml volume) via an entry port (initial inoculum, about 10⁶ CFU/ml) and the model was run for 18 h to allow organism growth to reach equilibrium at a density of about 10⁸ CFU/ml. Gemifloxacin (328 μl) was added to the dosing chamber. Samples were taken from the central chamber throughout the 48-h period, that is, at 0, 1, 2, 3, 4, 5, 6, 7, 10, 12, 22, 24, 25, 26, 27, 28, 29, 30, 31, 34, 36, 46, and 48 h for assessment of viable bacteria. The bacteria were quantified without dilution and after a 1/1,000 dilution in saline using a Spiral Plater (Don Whitley Spiral Systems, Shipley, United Kingdom). The minimum detection level was 2 × 10² CFU/ml. In addition aliquots were taken at the same time intervals and were stored at −70°C for measurement of gemifloxacin concentrations. Samples were assayed by bioassay with Escherichia coli NCTC 10418 as the indicator organism (5). All standards and samples were prepared and diluted as necessary in the same concentration of brain heart infusion broth used in the model. The limit of detection was 0.03 mg/liter with a percent coefficient of variation (% CV) of 8.3%. All pharmacokinetic simulations and killing-curve determinations were performed in triplicate.

Pharmacodynamics, measurement of antibacterial effect, and statistical analysis.

Antibacterial effect was assessed by calculating the log change in viable count from time zero at 12 (Δ12), 24 (Δ24), 36 (Δ36), and 48 h (Δ48). The maximum reduction in viable count was also calculated (Δmax). In addition, the area under the bacterial-kill curve (AUBKC, in log CFU · h/ml) was calculated by the log linear trapezoidal rule for the periods of 0 to 24 h (AUBKC₂₄) and 0 to 48 h (AUBKC₄₈) after standardization of the inoculum. The time taken for the inoculum to fall to 99.9% of its time zero value (T99.9) was also determined. The variability in measurements of antibacterial effect was assessed by calculating the % CV for each simulation and then using the following equation: median −% CV = (standard deviation/mean) × 100. For pharmacodynamic analysis the AUC/MIC, C_max/MIC, and T > MIC were calculated for the 48-h observation period.

The AUBKC₄₈ was compared to AUC/MIC, C_max/MIC, and T > MIC using an inhibitory sigmoidal E_max model using Win Nonlin Software (Scientific Consulting, Cary, N.C.). The correlation between the pharmacodynamic variables was assessed using the Spearman rank correlation coefficient. Subsequently, weighted least-squares regression analysis was used to examine the combined effects of AUC/MIC, C_max/MIC, and T > MIC on AUBKC₄₈. The weights were proportional to the number of replicate experiments and the variability between replicates. (Robust standard errors were calculated with adjustment for clustering of replicate experience.) Models were compared using t statistics and the r² model. Cox proportional-hazards regression was used to assess whether AUC/MIC, C_max/MIC, or T > MIC was predictive of T99.9. Changes in −2-log likelihood were used to compare different models.

RESULTS

MICs and MBCs.

The gemifloxacin MICs and MBCs for each strain were as follows: strain 18964, 0.016 and 0.04 mg/liter; strain 18330, 0.06 and 0.12 mg/liter; strain 18327, 0.10 and 0.14 mg/liter; strain 18907, 0.16 and >0.30 mg/liter; and strain 18329, 0.24 and 0.46 mg/liter.

The ciprofloxacin MICs for each strain were as follows: strain 18964, 1.0 mg/liter; strain 18330, 4 mg/liter; strain 18327, 16 mg/liter; strain 18907, >32 mg/liter; and strain 18329, >32 mg/liter.

Pharmacokinetic curves.

There was good agreement between target and actual gemifloxacin concentrations in the model (data not shown). The target pharmacodynamic parameter values associated with each simulation are shown in Table 1.

TABLE 1.

Pharmacodynamic parameters associated with S. pneumoniae strain susceptibilities and the pharmacokinetics modeled

Strain	MIC (mg/liter)	Pharmacodynamic parametersa
		AUC/MIC			Cmax/MIC			T > MIC
		640 × 1	320 × 2	160 × 4	640 × 1	320 × 2	160 × 4	640 × 1	320 × 2	160 × 4
18964	0.016	1,081	1,081	1,219	131	68	42	100	100	100
18330	0.06	288	288	325	35	18	11	80	100	100
18327	0.10	173	173	195	21	11	6.8	54	84	100
18907	0.16	108	108	122	13	6.8	4.2	47	61	94
18329	0.24	72	72	81	8.8	4.5	2.8	38	42	77

^aFor each parameter, values are given for three dosing regimens (given as dose in milligrams × the number of times administered in a 48-h period). 

Bacterial-killing curves.

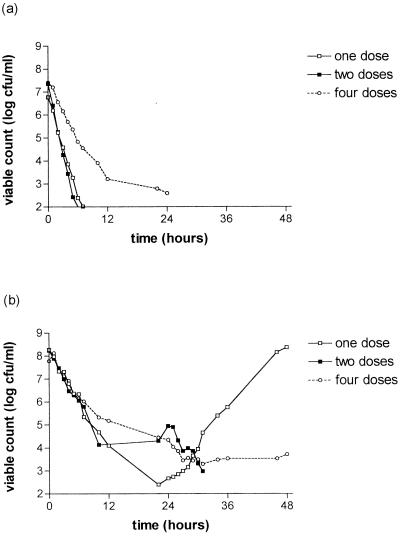
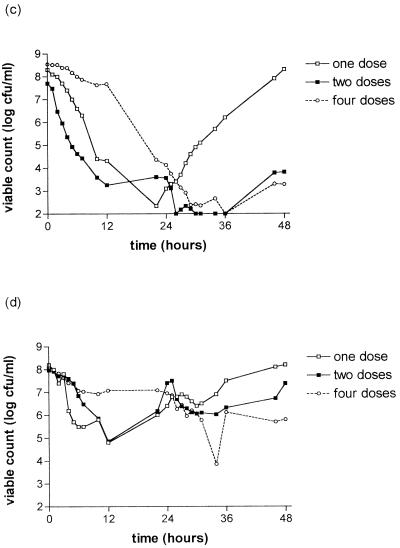
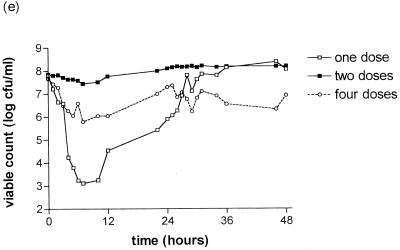
The killing curves of the S. pneumoniae strains after exposure to gemifloxacin are shown in Fig. 1. There is a clear relationship between strain susceptibility and clearance from the model. Strain 18964 (MIC, 0.016 mg/liter) was cleared from the model within 25 h with all simulations. For strain 18330 (MIC, 0.06 mg/liter), clearance was only achieved for the simulation of 320 mg every 24 h; growing back occurred with the dose of 640 mg every 48 h with this strain. Strains 18907 (MIC, 0.16 mg/liter) and 18329 (MIC, 0.24 mg/liter) were cleared less well than those for which the MIC was ≤0.06 mg/liter. The simulation of 160 mg every 12 h seemed to be associated with slower clearance in the first 24 h than the other simulations for strains 18964, 18330, 18327, and 18907.

FIG. 1.

Bactericidal effect of gemifloxacin at simulated concentrations in serum of 640 mg every 48 h (one dose), 320 mg every 24 h (two doses), or 160 mg every 12 h (four doses) on S. pneumoniae strain 18964 (MIC, 0.016 mg/liter) (a); strain 18330 (MIC, 0.06 mg/liter) (b); strain 18327 (MIC, 0.10 mg/liter) (c); strain 18907 (MIC, 0.16 mg/liter) (d); and strain 18929 (MIC, 0.24 mg/liter) (e).

Marked bacterial regrowth occurred with the 640-mg simulation with strains 18327, 18907, and 18329 (MICs, ≥0.1 mg/liter), but some regrowth was seen with other simulations.

The antibacterial effect was described by the following measurements: Δ12, Δ24, Δ36, Δ48, Δmax, AUBKC₂₄, AUBKC₄₈, and T99.9 (Table 2). AUBKC₂₄ and AUBKC₄₈ decreased as the MIC decreased, as did T99.9. There was a trend for the simulation of 320 mg every 24 h to have the lowest AUBKC₄₈ for the strains for which the MIC was ≤ 0.1 mg/liter.

TABLE 2.

Antibacterial effect measures for each S. pneumoniae strain with each gemifloxacin dose simulation

Strain and MIC (mg/liter)	Regimen (n)	Change in viable count (log CFU/ml)					AUBKC (log CFU · h/ml)		T99.9 (h)
		Δ12	Δ24	Δ36	Δ48	Δmax	AUBKC24	AUBKC48
18964 (0.016)	160 × 4 (4)	−4.2 ± 0.8	−4.8 ± 1.1	−5.0 ± 1.1	−4.8 ± 1.4	−5.2 ± 0.6	63.2 ± 14.6	89.2 ± 40.2	12.3 ± 5.3
	320 × 2 (3)	−5.3 ± 0.3	−5.3 ± 0.3	−5.3 ± 0.3	−5.3 ± 0.3	−5.3 ± 0.3	31.4 ± 6.1	31.4 ± 6.1	3.3 ± 0.6
	640 × 1 (3)	−4.8 ± 0.3	−4.8 ± 0.3	−4.8 ± 0.3	−4.8 ± 0.3	−4.8 ± 0.3	45.5 ± 6.7	45.5 ± 6.7	4.6 ± 0.6
18330 (0.06)	160 × 4 (4)	−2.6 ± 2.3	−3.4 ± 1.9	−4.2 ± 0.9	−4.0 ± 1.6	−4.5 ± 0.7	90.1 ± 40.5	132.6 ± 63.3	16.2 ± 11
	320 × 2 (3)	−5.2	−3.4 ± 1.4	−6.3 ± 0.02	−6.2 ± 0.02	−6.2 ± 0.02	67.3 ± 24.9	84.8 ± 31.4	7.3 ± 2.5
	640 × 1 (3)	−4.2 ± 0.3	−5.6 ± 0.2	−2.5 ± 0.2	+0.1 ± 0.5	6.2 ± 0.4	47.0 ± 4.5	130.5 ± 15.5	7.6 ± 1.9
18327 (0.10)	160 × 4 (4)	−0.8 ± 0.2	−4.4 ± 0.4	−6.4 ± 0.4	−5.2 ± 1.1	−6.6 ± 0.05	104.2 ± 4.9	118.1 ± 6.6	22.0 ± 0
	320 × 2 (4)	−4.5 ± 0.8	−4.1 ± 0.5	−5.6 ± 0.4	−3.9 ± 1.3	−5.7 ± 0.2	59.7 ± 12.9	82.9 ± 16.2	7.2 ± 3.0
	640 × 1 (3)	−3.4 ± 2.8	−1.9 ± 2.2	−2.2 ± 0.7	0 ± 0.3	6.2 ± 0.4	47.4 ± 4.5	130.5 ± 15.5	19.3 ± 8.0
18907 (0.16)	160 × 4 (5)	−1.0 ± 1.9	−1.2 ± 1.5	−2.0 ± 1.99	−2.3 ± 2.1	−2.8 ± 2.0	122.6 ± 33.2	217.7 ± 67.5	35.8 ± 16
	320 × 2 (3)	−3.1 ± 0.8	−0.6 ± 1.4	−1.6 ± 2.1	−0.6 ± 1.2	−3.9 ± 0.9	103.0 ± 2.8	213.5 ± 46.6	24.4 ± 17
	640 × 1 (3)	−3.4 ± 2.8	−1.9 ± 2.2	−0.8 ± 1.7	0 ± 0.7	−4.6 ± 0.8	88.1 ± 39.1	209.6 ± 33.7	153 ± 13.3
18329 (0.24)	160 × 4 (3)	−1.2 ± 1.0	−0.4 ± 1.0	−1.2 ± 1.4	−0.8 ± 3.3	−3.3 ± 1.9	120.9 ± 26.4	243.4 ± 39.9	41.1 ± 16.4
	320 × 2 (6)	−0.01 ± 0.2	+0.2 ± 0.4	+0.3 ± 0.4	+0.3 ± 0.4	−0.5 ± 0.2	142.5 ± 2.8	293.8 ± 12.1	>48
	640 × 1 (3)	−3.3	−1.9 ± 0.3	+0.3 ± 0.3	+0.3 ± 0.3	−4.7 ± 0.1	70.2 ± 4.9	210.5 ± 15.4	4.6 ± 1.2

Pharmacodynamics of antibacterial effect.

The variability of each measurement of antibacterial effect was tested by calculating the % CV. The % CV could be calculated for 9 of the 15 simulations for Δmax and Δ48 and was 17 and 183%, respectively. The % CV could not be calculated for all simulations for Δmax and Δ48, as two measurements of antibacterial effect gauged by bacterial counts were below the minimum level of detection. The % CVs for T99.9 and AUBKC₄₈ were 42 and 19%. Univariate analysis of the relationship between AUC/MIC, C_max/MIC, or T > MIC and AUBKC₄₈ and T99.9 was performed (data not shown). This indicated that AUBKC₄₈ and T99.9 decreased with increasing AUC/MIC, C_max/MIC, and T > MIC. There is a strong correlation between the pharmacodynamic parameters by Spearman's rank correlation coefficient (95% confidence intervals): for AUC/MIC versus C_max/MIC, r = 0.77 (0.42 to 0.92), and for AUC/MIC versus T > MIC, r = 0.87 (0.6 to 0.96). C_max/MIC was less correlated to T > MIC: r = 0.42 (−0.14 to 0.77).

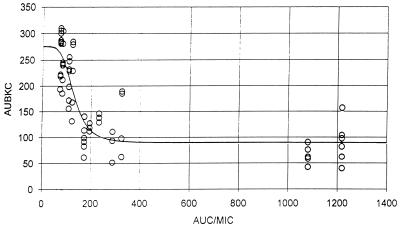
Untransformed AUBKC₄₈ was related to AUC/MIC, C_max/MIC, and T > MIC using an inhibitory E_max model. The relationship between AUC/MIC and AUBKC₄₈ (Fig. 2) could be adequately described in this model, as judged by Akaike information criteria and plots of the residuals against fitted values. The model fit was worse for T > MIC and C_max/MIC.

FIG. 2.

Gemifloxacin activity against S. pneumoniae strains for which MICs are different. The relationship between AUBKC₄₈ and AUC/MIC is shown. ○, observed data points; —, predicted pattern.

Cox's proportional-hazards regression was used to examine the ability of the three pharmacodynamic parameters to predict the measurements of antibacterial effect (T99.9). Experiments where T99.9 had not been reached by 48 h were censored at that point. Each parameter was grouped into four categories: group 1, AUC/MIC < 100, C_max/MIC < 5, and T > MIC < 50; group 2, AUC/MIC = 100 to 199, C_max/MIC = 5 to 9.9, and T > MIC = 51 to 79; group 3, AUC/MIC = 200 to 999, C_max/MIC = 10 to 29.9, and T > MIC = 80 to 99; and group 4, AUC/MIC > 999, C_max/MIC > 30, and T > MIC > 99. For AUC/MIC and T > MIC, the ln(relative risk) increased linearly across the four categories, but for C_max/MIC, there was some evidence to suggest that change was not linear (P = 0.06). Thus, AUC/MIC and T > MIC were fitted as ordered in categories, and C_max/MIC was modeled using separate categories. Univariate analysis suggested that all three parameters were predictive of T99.9 (P < 0.05), but when considered together in a multivariate model, both AUC/MIC and T > MIC failed to reach significance (P = 0.27). The relative risk for each of the four C_max/MIC categories is shown in Table 3. The risk for systems with a C_max/MIC of >5 was significantly greater than for those with a C_max/MIC of <5, but the relative risk did not differ significantly between groups with a C_max/MIC of >5.

TABLE 3.

Relative risk for each of the four categories of C_max/MIC

Cmax/MIC	Relative risk	95% Confidence interval
<5	1.0
5–9.9	7.0	2.2–27.2
10–29.9	11.6	4.3–31.8
>30	20.7	2.3–68.3

AUBKC₄₈ was used as the second measurement of antibacterial effect and was analyzed using weighted least-squares regression.

There was no evidence to suggest that C_max/MIC was predictive of AUBKC₄₈ (P = 0.65), but both T > MIC and AUC/MIC were significant predictors, as was (AUC/MIC)². The estimated regression model is shown in Table 4. The estimated regression coefficients suggest that as AUC/MIC and T > MIC increase, AUBKC₄₈ decreases.

TABLE 4.

Estimated regression model using AUBKC₄₈ as measurement of antibacterial effect

Variable	Coefficient	95% Confidence interval
AUC/MIC	−0.88	−1.34–0.41
(AUC/MIC)2	0.0006	0.0002–0.001
T > MIC	−1.20	−2.18–0.21
Constant	384.97	314.9–455.0

As T > MIC may be related to regrowth, as in the simulations of 640 mg every 48 h, and as this would have an impact on AUBKC₄₈, we repeated the analysis, including only simulations where the T > MIC was >75%. From the linear model there was no evidence to suggest that C_max/MIC or T > MIC was predictive of AUBKC₄₈ (P = 0.89 and 0.27, respectively), but AUC/MIC was found to be a significant predictor, as was the squared term (AUC/MIC)².

DISCUSSION

The present data add to our understanding of fluoroquinolone pharmacodynamics in several ways. Firstly, they show that gemifloxacin is an effective antipneumococcal agent. Strains for which MICs were ≤0.1 mg/liter were cleared from the model by 24 to 36 h with the 320-mg once-daily simulations. The antibacterial effect was poorer with those strains for which the MIC was ≥0.16 mg/liter, and little or no killing was observed when the MIC was 0.24 mg/liter. Data on MIC distribution for S. pneumoniae indicate MICs at which 90% of the isolates tested are inhibited to be in the range of 0.03 to 0.06 mg/liter (20). This suggests that gemifloxacin will have clinically useful antipneumococcal activity, and there are supportive animal studies of respiratory and central nervous system infection using strains for which MICs are up to 0.125 mg/liter (10, 19, 21). When human pharmacokinetics of 320-mg gemifloxacin were modeled in rats to produce an AUC similar to that in humans, a >4-log reduction in viable pneumococci in lung tissue was observed after 3 days of therapy. The MICs for all the S. pneumoniae strains were ≤0.03 mg/liter. Recent reports from clinical trials confirm gemifloxacin's activity against pneumococci (T. File, B. Schlemmer, T. Garau, B. Siquier, K. Hendrick, C. Young, and the Gemifloxacin 049 Study Group, 3rd Eur. Congr. Chemother., abstr. M129, p. 55, 2000).

The data also indicate that simulations of 320 mg once daily compared to 640 mg every 48 h or 160 mg every 12 h tend to have the best antimicrobial effect—with the exception of strain 18329 (MIC = 0.24 mg/liter). Regrowth after 24 h was most notable with the 640-mg simulation, with MICs of 0.06 to 0.16 mg/liter, while for the 160-mg simulation, clearance from the model was slower in the first 12 h than for the 320- or 640-mg simulation.

Over the last 2 to 3 years it has been suggested that the pharmacodynamic parameters (AUC/MIC, C_max/MIC, and T > MIC) which predict fluoroquinolone's effect against gram-negative bacteria such as Pseudomonas aeruginosa could not be applied to gram-positive pathogens—in particular, S. pneumoniae (Wright et al., Abstr. 98th Gen. Meet. Am. Soc. Microbiol.). Using an in vitro pharmacodynamic model and testing ciprofloxacin, levofloxacin, and trovafloxacin against two strains of S. pneumoniae, it was not possible to relate AUC/MIC or C_max/MIC to T99.9 and/or regrowth (Wright et al., Abstr. 98th Gen. Meet. Am. Soc. Microbiol.). In contrast, these data show that it is possible to use time-to-event analysis to relate T99.9 to pharmacodynamic parameters. Multivariate analysis indicates that C_max/MIC was best related to T99.9. A value of >5 for C_max/MIC was optimal, which is in close agreement with other data, using different measurements of antibacterial effect to assess the effect of ciprofloxacin, ofloxacin, or levofloxacin against multidrug-resistant S. pneumoniae (K. J. Madaras-Kelly, T. Demasters, D. Soaves, and M. McLaughling, Abstr. 37th Intersci. Conf. Antimicrob. Agents Chemother., abstr. A-27, 1997). A similar data analysis testing the activity of moxifloxacin against a group of gram-positive and gram-negative pathogens indicated that AUC/MIC but not T > MIC could be related to T99.9. Due to the experimental design, the individual effects of AUC/MIC and C_max/MIC could not be distinguished in that analysis (16). However, in this work it should be remembered that there is a significant covariability of the pharmacodynamic parameters, as doses used in humans or doses close to those used in humans were employed.

Further controversy exists surrounding the magnitude of the AUC/MIC required to maximize the outcome. A number of authors have shown that S. pneumoniae clearance from in vitro models by ciprofloxacin, levofloxacin, ofloxacin, or trovafloxacin occurs at an AUC/MIC of 30 to 50 (11–13). This contrasts with other in vitro model data with P. aeruginosa, which indicate that an AUC/MIC of up to 200 to 500 is required to maximize effect (17). The data on P. aeruginosa correlate with human data collected mainly by treating gram-negative infection in patients with pneumonia in intensive-care units (9). Our data indicate that by the use of E_max curve fitting, AUC/MIC is best related to antibacterial effect, as measured by AUBKC₄₈, and visual inspection of the curve indicates that the maximal effect occurs at an AUC/MIC of 300 to 400. This is in keeping with our own data on other gram-positive pathogens tested against moxifloxacin. The moxifloxacin AUC/MIC needed to produce the maximal effect against Staphylococcus aureus and beta-hemolytic streptococci was >150 (14). Data produced using five strains of S. pneumoniae for which the moxifloxacin MIC range was 0.08 to 3.6 mg/liter indicated little antibacterial effect when the AUC/MIC was <100 (15). Combining these data suggests that the optimal AUC/MIC to produce a bactericidal effect on gram-positive bacteria is similar to that for gram-negative pathogens: definitive data from human pharmacodynamic studies are awaited.

A number of antibacterial effect measurements are used to assess efficacy in in vitro pharmacokinetic models. In this study we used T99.9 but showed again that it is a highly variable measurement (16). This may explain why some groups have not been able to correlate it to pharmacodynamic parameters. As may be expected, C_max/MIC is related to T99.9, as T99.9 depends on speed of kill, which for concentration-dependent agents such as fluoroquinolones is related to drug concentration and pathogen susceptibility (MIC). Data collected with ciprofloxacin in simulations of 500 mg every 12 h or 1,000 mg every 24 h indicated that the 1,000-mg simulation had advantages in terms of early bactericidal action (3). It is interesting that regrowth was a most marked feature of the experiments using a single 640-mg simulation. T > MIC is likely to be related to regrowth in in vitro models, and in the multivariate analysis of pharmacodynamic correlations with AUBKC₄₈, both AUC/MIC and T > MIC were predictive. When only data with T > MICs of >75% were analyzed, only AUC/MIC was predictive. It is already known from the work of Firsov et al. that the use of measurement of antimicrobial effect which depends on regrowth (intensity of effect) is strongly related to T > MIC and fluoroquinolone half-life in serum (8; Firsov and Zinner, 8th Int. Symp. New Quinalones). However, it is unclear whether in immunocompetent animals or humans the small number of bacteria needed to produce regrowth in in vitro models would be cleared by the immune system.

The complex relationships between AUC/MIC, C_max/MIC, and T > MIC in predicting fluoroquinolone's antibacterial effect in this in vitro model are a reflection of the situation in animal models (9). A review of the use of fluoroquinolones to treat experimental endocarditis due mainly to gram-positive bacteria indicated that an AUC/MIC of >100, C_max/MIC of >8, and T > MIC of 100% were significantly associated with lower numbers of CFU per gram of vegetation. However, AUC/MIC showed the best correlation with numbers of CFU per gram of vegetation. These data are similar in showing that although AUC/MIC best predicts gemifloxacin's antibacterial effect, C_max/MIC and T > MIC also have a role.

In conclusion, these data indicate that gemifloxacin is an effective antipneumococcal agent. In our pharmacokinetic model system, AUBKC₄₈ is the least variable measurement of antibacterial effect and AUC/MIC is its best predictor. However, speed of kill as measured by T99.9 is best predicted by C_max/MIC, and prolongation of the dosing interval with a reduction in T > MIC results in bacterial regrowth in the model and increases the importance of T > MIC as a predictor of AUBKC₄₈. In conclusion, gemifloxacin showed concentration-dependent activity against S. pneumoniae, its effect is predicted best by AUC/MIC, and once-daily dosing seems the most suitable regimen.